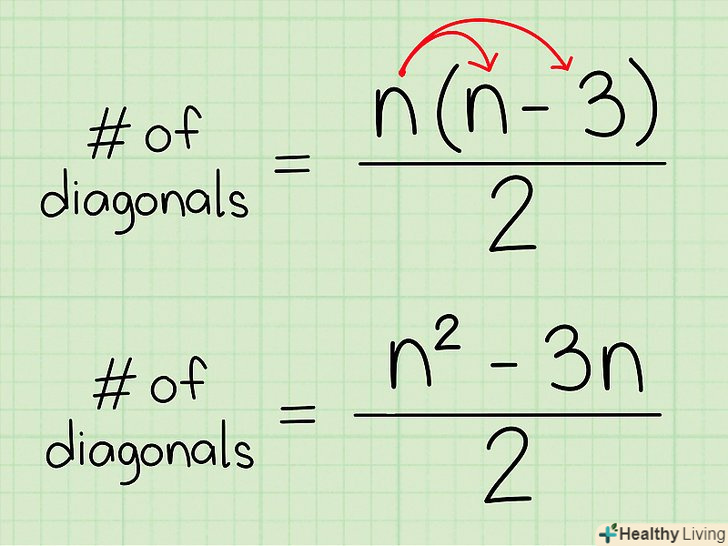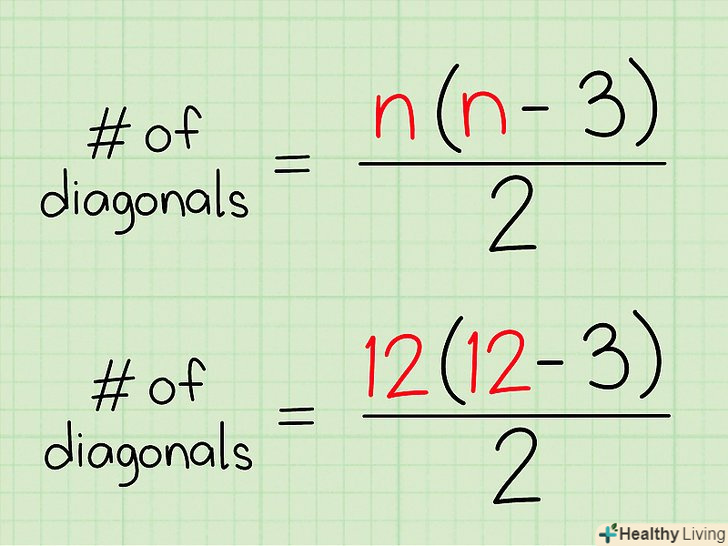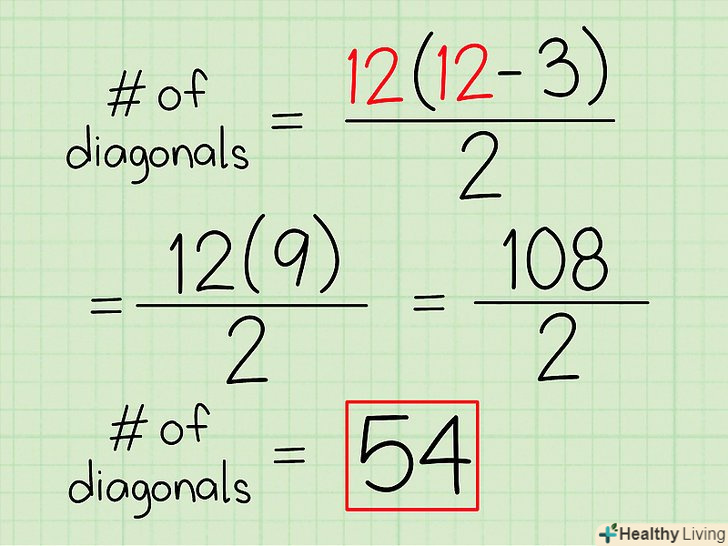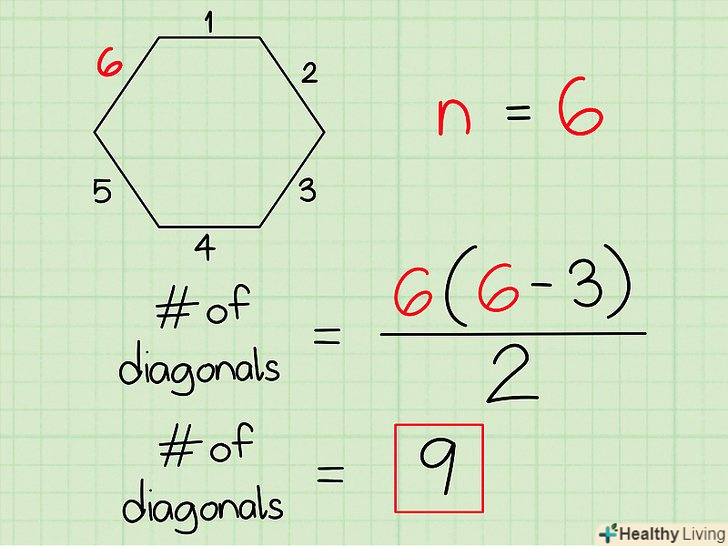1. Головна
    2. Геометрія
    3. Як знайти число діагоналей в багатокутнику: 11 кроків

Як знайти число діагоналей в багатокутнику: 11 кроків

Знаходження числа діагоналей є найважливішим навиком, який стане в нагоді при вирішенні геометричних завдань. Це не так складно, як здається-просто потрібно запам'ятати формулу. Діагональ-це відрізок, що з'єднує будь-які дві несуміжні вершини багатокутника.[1] багатокутник-це будь-яка фігура з як мінімум трьома сторонами. За допомогою нескладної формули можна знайти кількість діагоналей в будь-якому багатокутнику, наприклад, з 4 сторонами або з 4000 сторін.

Метод1 З 2:
Малювання діагоналей

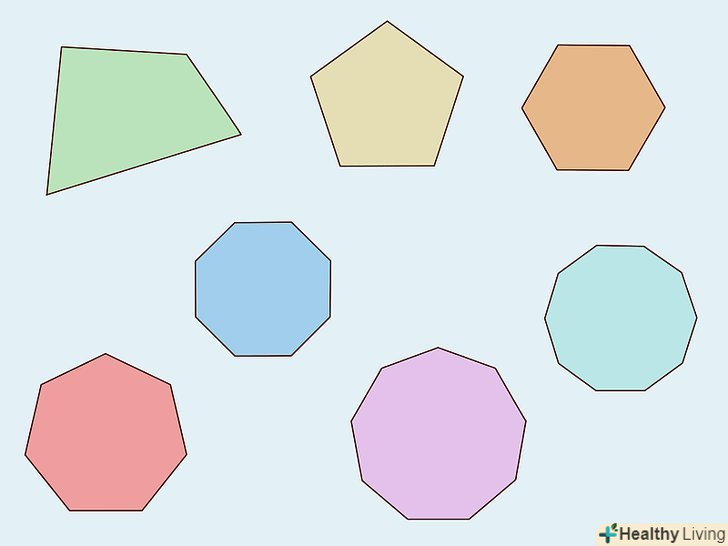
  1. Запам'ятайте назви багатокутників.спочатку потрібно знайти число сторін багатокутника. Це можна зробити за назвою будь-якого багатокутника. Ось назви найпоширеніших багатокутників:[2]
    • Чотирикутник: 4 сторони
    • П'ятикутник: 5 сторін
    • Шестикутник: 6 сторін
    • Семикутник: 7 сторін
    • Восьмикутник: 8 сторін
    • Дев'ятикутник: 9 сторін
    • Десятикутник: 10 сторін
    • Зверніть увагу, що у трикутника діагоналей немає.[3]
  2. Намалюйте багатокутник.щоб знайти число діагоналей в квадраті, намалюйте його. Найпростіший спосіб знайти число діагоналей - це намалювати правильний багатокутник (в такому багатокутнику всі сторони рівні) і порахувати кількість діагоналей. Запам'ятайте: неправильний багатокутник матиме таку ж кількість діагоналей, що і правильний (при однаковому числі сторін).[4]
    • Щоб намалювати багатокутник, скористайтеся лінійкою; намалюйте замкнуту фігуру зі сторонами однакової довжини.
    • Якщо ви не знаєте, як виглядає багатокутник, пошукайте картинки в Інтернеті. Наприклад, знак "Стоп" - це восьмикутник.
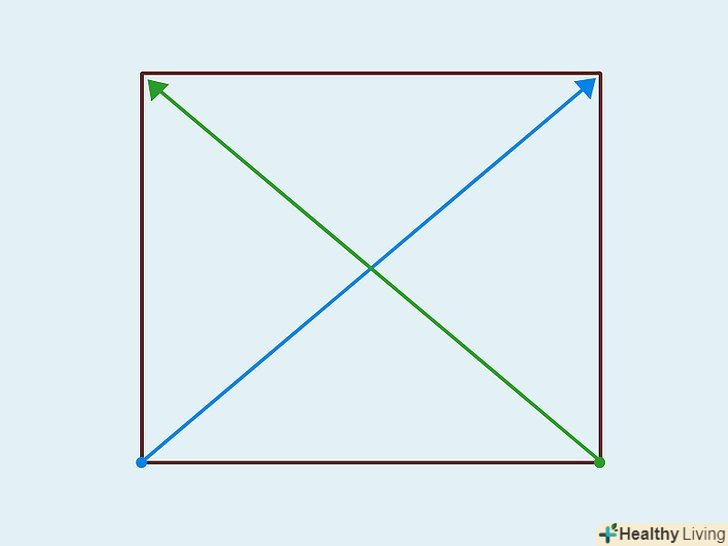
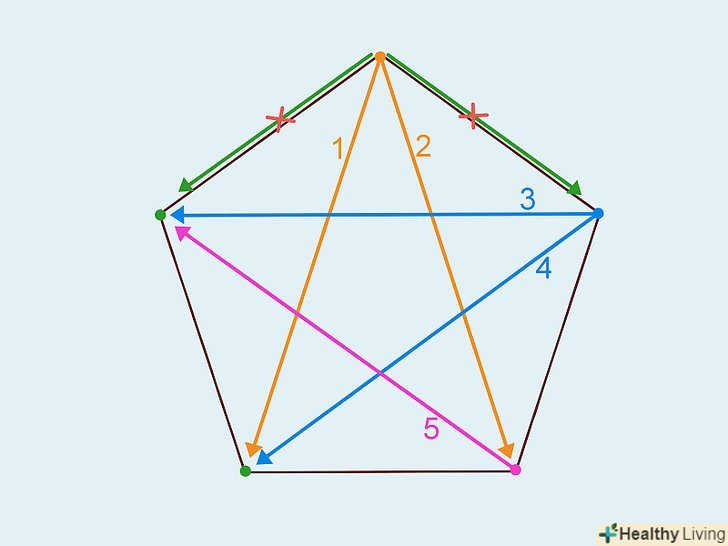
  3. Намалюйте діагоналі. діагональ-це відрізок, що з'єднує будь-які дві несуміжні вершини багатокутника.[5] з однієї (будь-якої) вершини багатокутника проведіть діагоналі до інших (несуміжних) вершин.
    • У квадраті проведіть одну діагональ з нижнього лівого кута в правий верхній кут, а другу – з нижнього правого кута в лівий верхній кут.
    • Намалюйте діагоналі різних кольорів, щоб швидше порахувати їх.[6]
    • Зверніть увагу, що застосовувати цей метод до багатокутників, у яких більше 10 сторін, досить складно.
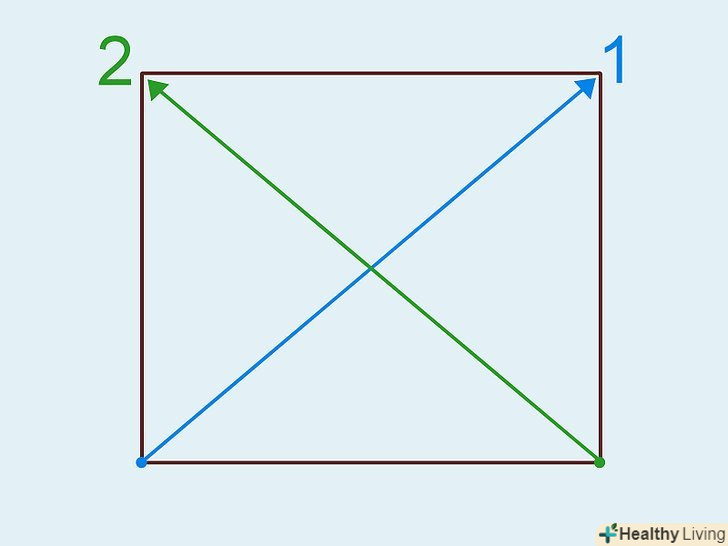
  4. Порахуйте діагоналі.можна вважати діагоналі під час того, як ви малюєте їх, або після того, як вони намальовані. Відзначайте діагоналі, які вже пораховані, щоб не заплутатися (особливо коли діагоналей багато і вони перетинаються).
    • У квадрата всього дві діагоналі - по одній на кожні дві вершини.[7]
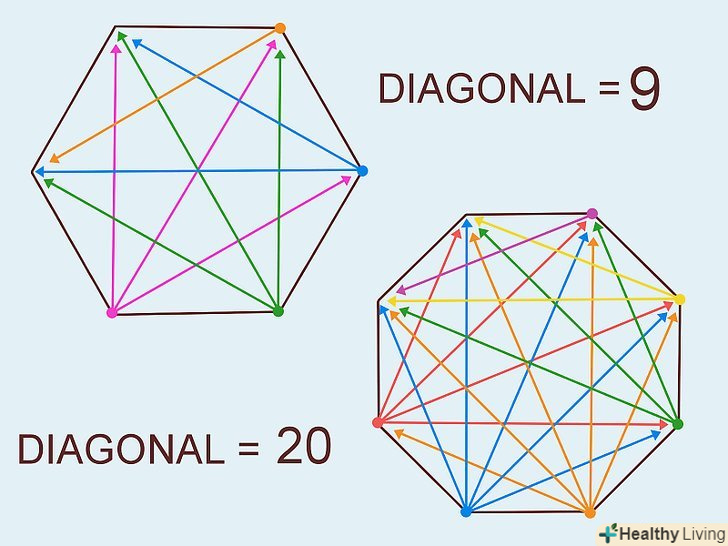
    • У шестикутника 9 діагоналей: по три діагоналі на кожні три вершини.
    • У семикутника 14 діагоналей. Якщо у багатокутника більше семи сторін, порахувати діагоналі досить складно, тому що їх занадто багато.
  5. Кожну діагональ рахуйте тільки один раз. з кожної вершини виходить кілька діагоналей, але це не означає, що число діагоналей дорівнює добутку числа вершин на число діагоналей, що виходять з кожної вершини. Тому акуратно вважайте діагоналі.[8]
    • Наприклад, у п'ятикутника (5 сторін) тільки 5 діагоналей. З кожної вершини виходить 2 діагоналі; якщо помножити число вершин на число діагоналей, що виходять з кожної вершини, отримаєте 10. Це невірна відповідь, як якщо б ви порахували кожну діагональ двічі.
  6. Попрактикуйтесь у визначенні числа діагоналей на деяких прикладах. Намалюйте різні багатокутники і порахуйте їх діагоналі. Цей метод застосуємо і до неправильних багатокутників. У разі увігнутого багатокутника деякі діагоналі лежать поза межами фігури.[9]
    • У шестикутника 9 діагоналей.
    • У семикутника 14 діагоналей.

Метод2 З 2:
Формула

  1. Запишіть формулу.Формула для обчислення числа діагоналей багатокутника: d = n(n-3) / 2, де d – число діагоналей, n – число сторін багатокутника.[10] використовуючи розподільну властивість, цю формулу можна записати так: d = (n2 - 3n)/2. Можна користуватися будь-якою формою представленої формули.
    • Ця формула для обчислення числа діагоналей багатокутника.
    • Зверніть увагу, що ця формула не застосовується до трикутників, тому що у трикутників діагоналей немає.[11]
  2. Визначте число сторін багатокутника.щоб використовувати наведену формулу, потрібно знати число сторін багатокутника. Число сторін можна з'ясувати за назвою багатокутника. Нижче наведені частини назв багатокутників.[12]
    • Чотирьох (4), п'яти (5), шести (6), семи (7), восьми (8), дев'яти (9), десяти (10), одинадцяти (11), дванадцяти (12 ), тринадцяти (13), чотирнадцяти (14), п'ятнадцяти (15) і так далі.
    • Якщо сторін занадто багато, то в назву багатокутника включається цифра. Наприклад, якщо у багатокутника 44 сторони, він називається 44-косинцем.
    • Якщо дано малюнок багатокутника, просто порахуйте його боку.
  3. Підставте число сторін у формулу.зробіть це після того, як знайдете число сторін багатокутника. Число сторін підставте замість n.[13]
    • Наприклад. У дванадцятикутника 12 сторін.
    • Запишіть формулу: d = n(n-3) / 2
    • Підставте число сторін: d = (12(12 - 3))/2
  4. Вирішіть рівняння.для цього не забудьте про певний порядок виконання математичних операцій. Почніть з віднімання, потім помножте, а потім розділіть. У підсумку ви отримаєте число діагоналей багатокутника.[14]
    • Наприклад: (12(12 - 3))/2
    • Віднімання: (12*9)/2
    • Множення: (108) / 2
    • Розподіл: 54
    • У дванадцятикутника 54 діагоналі.
  5. Попрактикуйтесь на інших прикладах.чим більше завдань ви вирішите, тим краще усвідомите процес обчислення. Також ви напевно запам'ятаєте формулу для обчислення числа діагоналей, що стане в нагоді на іспиті. Не забувайте, що представлена формула застосовна до багатокутника, у якого більше трьох сторін.
    • Шестикутник (6 сторін): d = n (n-3)/2 = 6(6-3)/2 = 6*3/2 = 18/2 = 9 діагоналей.
    • Десятикутник (10 сторін): d = n (n-3)/2 = 10(10-3)/2 = 10*7/2 = 70/2 = 35 діагоналей.
    • Двадцятикутник (20 сторін): d = n (n-3)/2 = 20(20-3)/2 = 20*17/2 = 340/2 = 170 діагоналей.
    • 96-косинець (96 сторін): 96(96-3)/2 = 96*93/2 = 8928/2 = 4464 діагоналей.

Джерела

  1. ↑ Https://www.mathsisfun.com/geometry/polygons-diagonals.html
  2. ↑ Http://mathcentral.uregina.ca/QQ/database/QQ.09.96/rosa1.html
  3. ↑ Https://www.mathsisfun.com/geometry/polygons-diagonals.html
  4. ↑ Https://www.mathsisfun.com/geometry/polygons-diagonals.html
  5. ↑ Https://www.mathsisfun.com/geometry/polygons-diagonals.html
  6. ↑ Http://intermath.coe.uga.edu/tweb/CPTM1/trushin/diagonals/diagonalsinapolygon.htm
  7. ↑ Http://intermath.coe.uga.edu/tweb/CPTM1/trushin/diagonals/diagonalsinapolygon.htm
  8. ↑ Http://www.mathopenref.com/polygondiagonal.html
  9. ↑ Https://www.mathsisfun.com/geometry/polygons-diagonals.html
  1. ↑ Https://www.mathsisfun.com/geometry/polygons-diagonals.html
  2. ↑ Https://www.mathsisfun.com/geometry/polygons-diagonals.html
  3. ↑ Http://www.infoplease.com/ipa/A0881983.html
  4. ↑ Http://www.mathopenref.com/polygondiagonal.html
  5. ↑ Http://www.mathopenref.com/polygondiagonal.html

Ще почитати: