Найбільш поширеною формулою для обчислення площі квадрата є наступна: S = a2. Але іноді в задачі дана тільки діагональ квадрата, тобто відрізок, що з'єднує протилежні вершини. Якщо Ви знайомі з прямокутними трикутниками, для обчислення площі квадрата можна скористатися формулою, яка включає діагональ.
Кроки
Частина1 З 2:
Обчислення площі по діагоналі
Частина1 З 2:
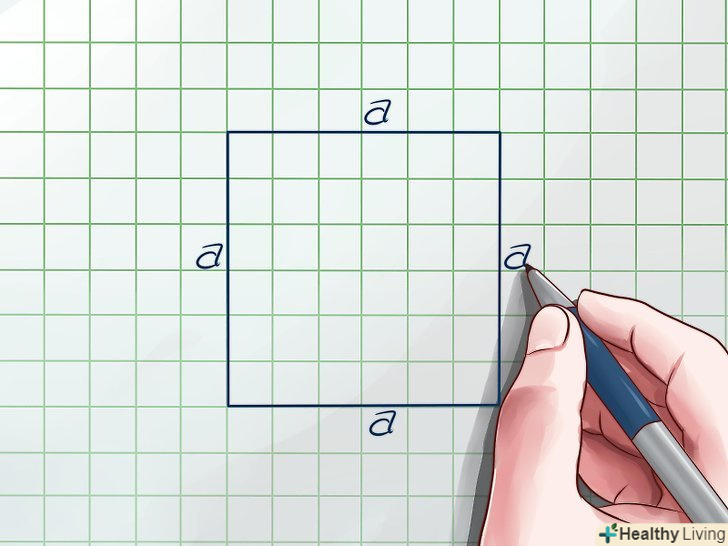
 Намалюйте квадрат. У квадрата чотири рівні сторони.[1] припустимо, що довжина кожної сторони дорівнює а.
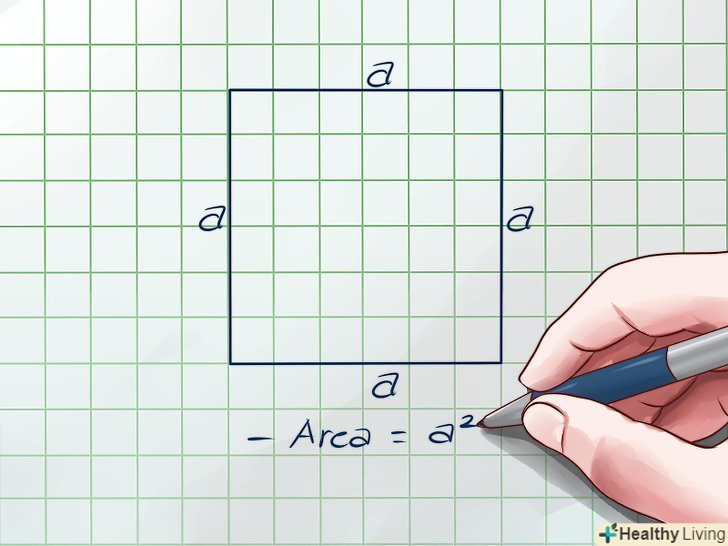
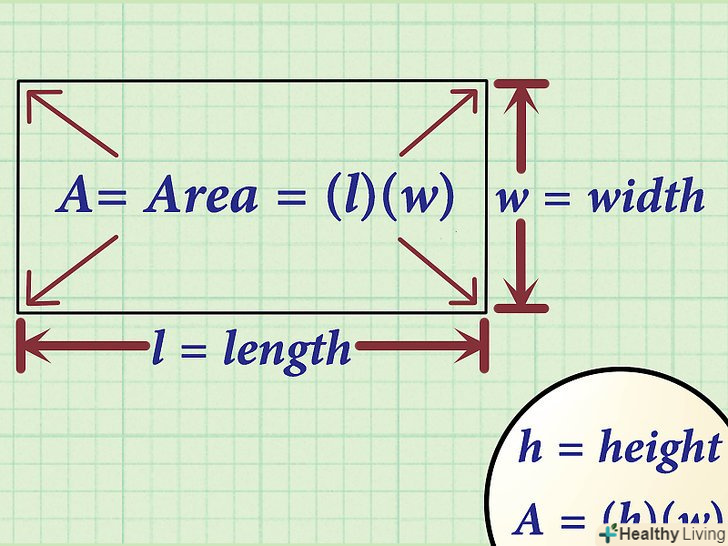
Намалюйте квадрат. У квадрата чотири рівні сторони.[1] припустимо, що довжина кожної сторони дорівнює а. Подивіться на основну формулу для обчислення площі квадрата. площа квадрата дорівнює добутку довжини на ширину. Так як кожна сторона квадрата дорівнює а, формула для обчислення площі квадрата: S = А х А = а2. Ця формула знадобиться далі.
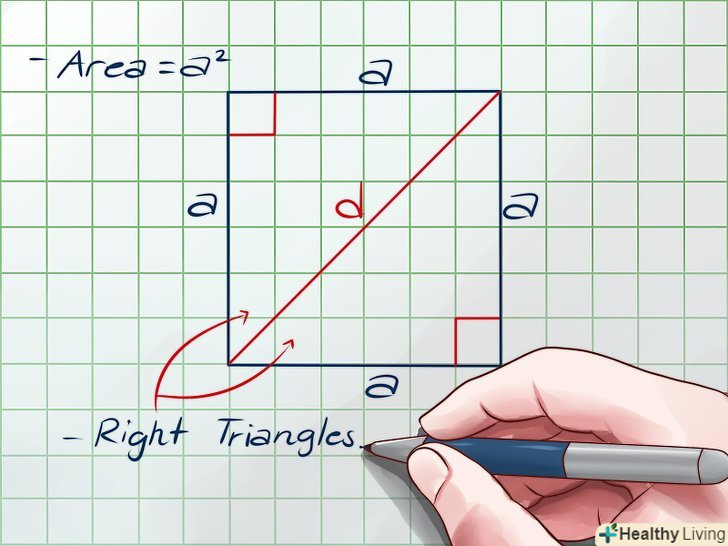
Подивіться на основну формулу для обчислення площі квадрата. площа квадрата дорівнює добутку довжини на ширину. Так як кожна сторона квадрата дорівнює а, формула для обчислення площі квадрата: S = А х А = а2. Ця формула знадобиться далі. З'єднайте два протилежні кути квадрата, щоб провести діагональ.припустимо, що довжина діагоналі дорівнює D. діагональ ділить квадрат на два прямокутних трикутника.
З'єднайте два протилежні кути квадрата, щоб провести діагональ.припустимо, що довжина діагоналі дорівнює D. діагональ ділить квадрат на два прямокутних трикутника. До одного з трикутниківЗастосуйте теорему Піфагора. за теоремою Піфагора[2] можна знайти гіпотенузу (найдовшу сторону) прямокутного трикутника:
До одного з трикутниківЗастосуйте теорему Піфагора. за теоремою Піфагора[2] можна знайти гіпотенузу (найдовшу сторону) прямокутного трикутника:, де А і b — катети, с-гіпотенуза. Розділивши квадрат на два прямокутних трикутника, застосуйте цю формулу до одного з них.
- Катетами прямокутного трикутника є сторони квадрата, кожна з яких дорівнює а.
- Гіпотенузою є діагональ квадрата, рівна d.
 Ізолюйте а2 на одній стороні формули.Пам'ятайте, що згідно з основною формулою для обчислення площі квадрата, вона дорівнює а2. Якщо ізолювати а2 на одній стороні формули, можна вивести нову формулу для обчислення площі квадрата.
Ізолюйте а2 на одній стороні формули.Пам'ятайте, що згідно з основною формулою для обчислення площі квадрата, вона дорівнює а2. Якщо ізолювати а2 на одній стороні формули, можна вивести нову формулу для обчислення площі квадрата.- Спростіть:
- Розділіть обидві сторони на 2:
- S =
- S =
 Скористайтеся цією формулою для вирішення завдання. отриману формулу S =
Скористайтеся цією формулою для вирішення завдання. отриману формулу S =можна застосовувати до будь-яких квадратів: просто підставте в неї значення діагоналі (замість d).
- Наприклад, діагональ квадрата дорівнює 10 см.
- S =
=
= 50 см2.
Частина2 З 2:
Додаткова інформація
Частина2 З 2:
- Знайдіть діагональ по стороні. [3] якщо сторона квадрата дорівнює А, а діагональ дорівнює d, теорема Піфагора запишеться так:
. За цією формулою можна обчислити діагональ, якщо сторона квадрата відома.
- Наприклад, якщо сторона квадрата дорівнює 7 см, його діагональ дорівнює d = 7√2 ∙ 9,9 см.
- Якщо калькулятора Немає, √2 ∙ 1,4.
- Знайдіть сторону по діагоналі. якщо діагональ відома, а формула для обчислення діагоналі
, розділіть обидві сторони формули на
та отримайте
- Наприклад, якщо діагональ квадрата дорівнює 10 см, то сторона
див.
- Якщо потрібно знайти і сторону, і площу по діагоналі, скористайтеся цією формулою, щоб обчислити сторону, а потім результат зведіть в квадрат, щоб обчислити площу: S =
см2. Такий метод не зовсім точний, тому що
є ірраціональним числом, тобто можуть мати місце помилки округлення.
- Наприклад, якщо діагональ квадрата дорівнює 10 см, то сторона
- Перевірте правильність формули. вірність математичного висновку формули S =
не викликає сумнівів, але чи можна перевірити правильність формули наочно? Припустимо, що сторона другого квадрата дорівнює d, тобто діагоналі першого квадрата; тоді Площа другого квадрата дорівнює
. Так як формула для обчислення площі S =
, можна зробити висновок, що Площа другого квадрата в два рази більше площі першого квадрата. Перевірте це наочно:
- На папері намалюйте перший квадрат. Переконайтеся, що всі сторони рівні.
- Виміряйте діагональ. Намалюйте другий квадрат: кожна його сторона повинна бути дорівнює діагоналі першого квадрата.
- Намалюйте копію першого квадрата, а потім виріжте три квадрати.
- Розріжте два менших квадрата так, щоб вони помістилися в більшому квадраті. Два менших квадрата повинні повністю покрити більший квадрат, що доводить, що площа більшого квадрата в два рази більше площі меншого квадрата.
Поради
- Якщо калькулятора немає, але необхідно отримати точне значення √2, витягніть коріньвручну. Наприклад, застосуйте метод Ньютона-Рафсона.[4]
- Наведена формула використовується в багатьох областях, в тому числі в кристалографії, хімії та техніці. Наприклад, за допомогою цієї формули можна обчислити площу ландшафту, який видно на власні очі або на фотографії/малюнку. Для цього виміряйте пройдений шлях, а потім проведіть уявну діагональ.
- Якщо ви віддаєте перевагу вивчати математику з наочними прикладами або хочете дізнатися, як використовувати діаграми і графіки в мистецтві, читайте статті на сайті wikiHow (наприклад, в категоріях «Математика», «графічні програми», «Офісні програми» та інших).