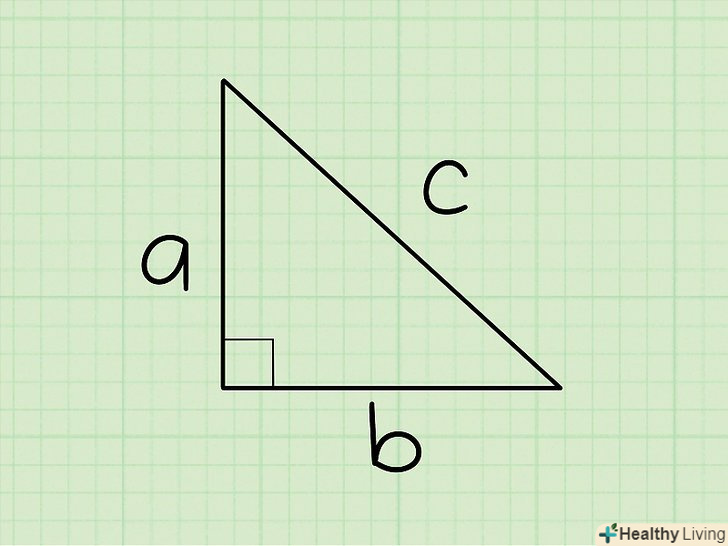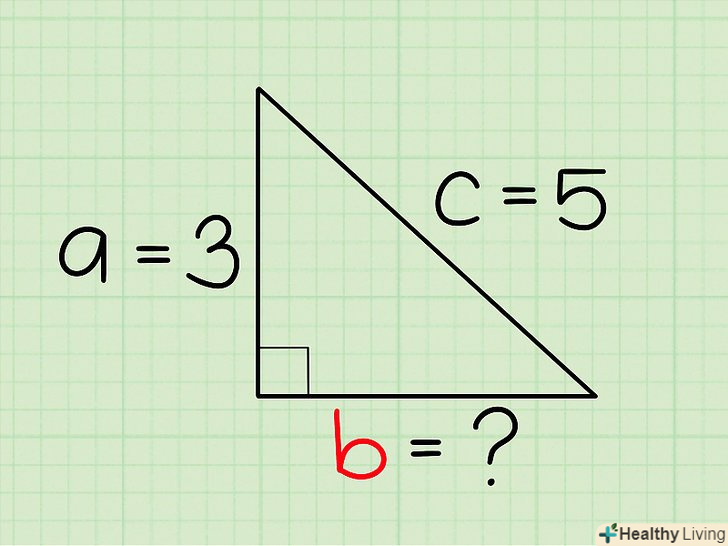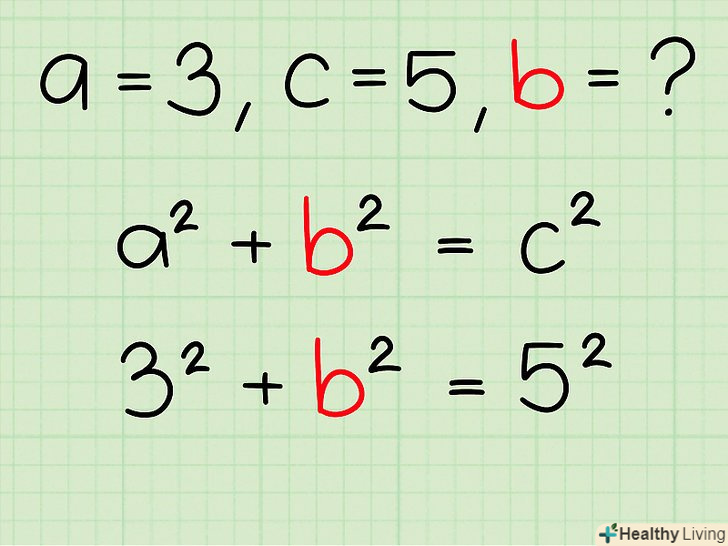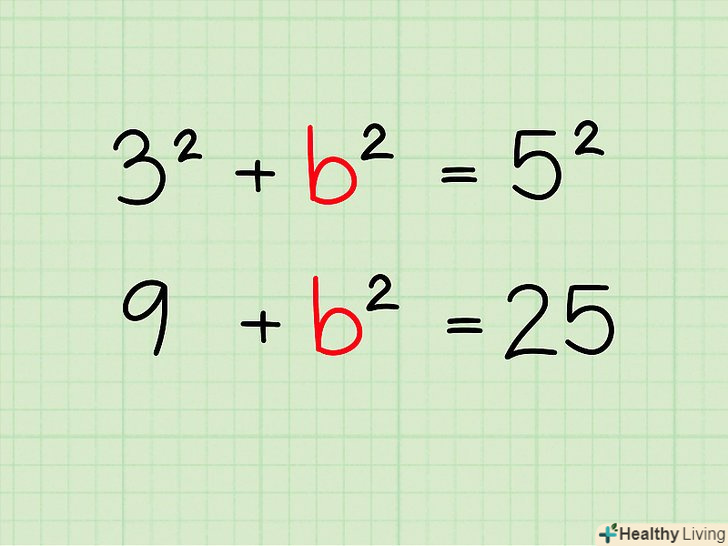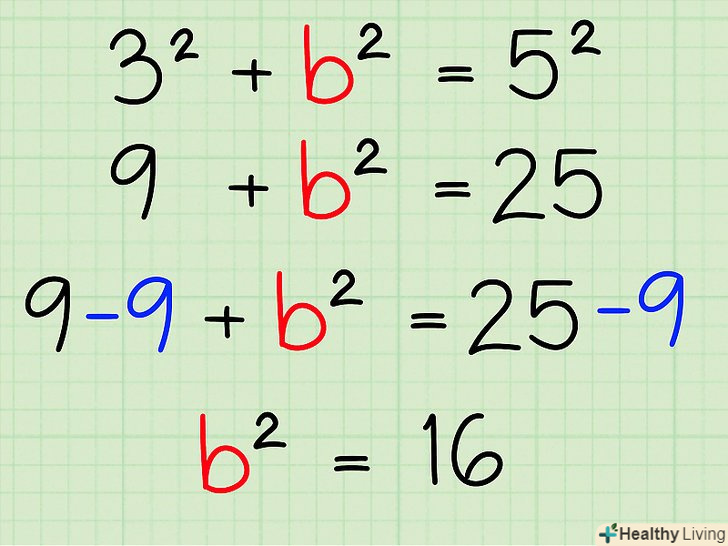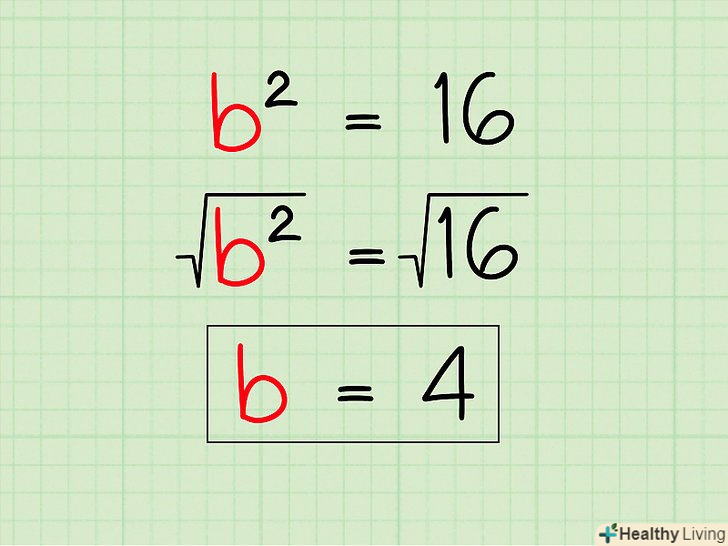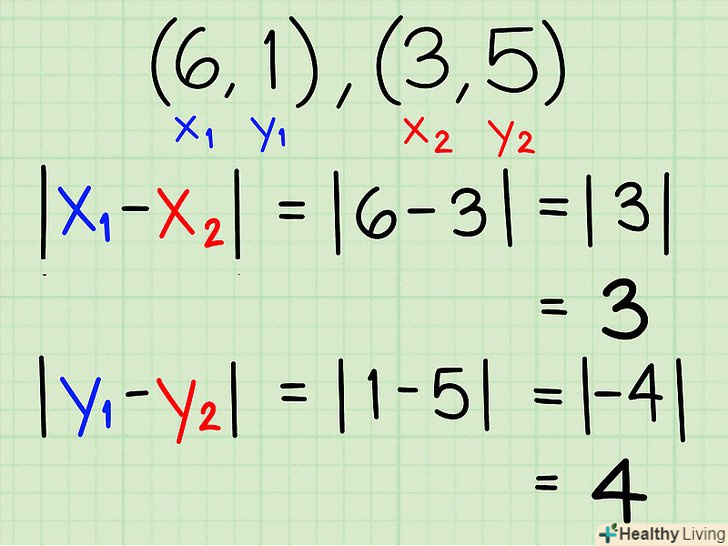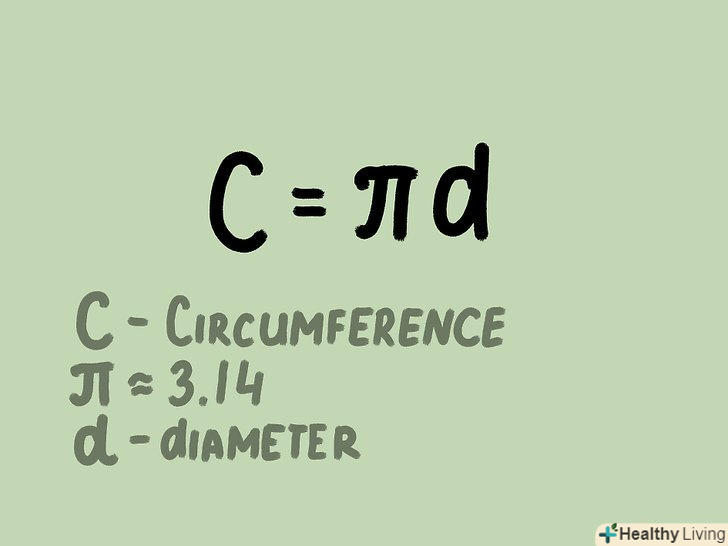Теорема Піфагора пов'язує три сторони прямокутного трикутника однією формулою, якою користуються досі. Теорема свідчить, що в прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи:A2 + b2 = c2, де a і b — катети трикутника (сторони, що перетинаються під прямим кутом), с — гіпотенуза трикутника. Теорема Піфагора застосовна в багатьох випадках, наприклад, за допомогою цієї теореми легко знайти відстань між двома точками на координатній площині.
Кроки
Метод1 З 2:
Знаходження сторін прямокутного трикутника
Метод1 З 2:
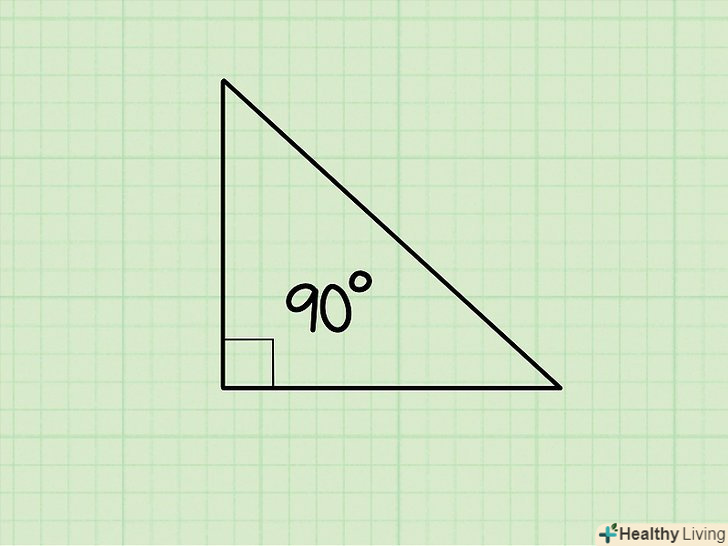
Переконайтеся, що даний Вам трикутник є прямокутним, так як теорема Піфагора застосовна тільки до прямокутних трикутників.у прямокутних трикутниках один з трьох кутів завжди дорівнює 90 градусам.- Прямий кут в прямокутному трикутнику позначається значком у вигляді квадрата, а не у вигляді кривої, яка позначає непрямі кути.
-
Позначте сторони трикутника. катети позначте як «А» і «b» (катети — сторони, що перетинаються під прямим кутом), а гіпотенузу — як " с " (гіпотенуза — найбільша сторона прямокутного трикутника, що лежить навпроти прямого кута).
-
Визначте, яку сторону трикутника потрібно знайти. Теорема Піфагора дозволяє знайти будь-яку сторону прямокутного трикутника (якщо відомі дві інші сторони). Визначте, яку сторону (a, b, c) потрібно знайти.
- Наприклад, дана гіпотенуза, рівна 5, і дан катет, рівний 3. В цьому випадку необхідно знайти другий катет. Ми повернемося до цього прикладу пізніше.
- Якщо дві інші сторони невідомі, необхідно знайти довжину однієї з невідомих сторін, щоб мати можливість застосувати теорему Піфагора. Для цього використовуйте основні тригонометричні функції (якщо вам дано значення одного з непрямих кутів).
-
Підставте в формулу a2 + b2 = c2 дані вам значення (або знайдені вами значення).Пам'ятайте, що a і b — це катети, а с — гіпотенуза.
- У нашому прикладі напишіть:32 + b2 = 52.
-
Зведіть в квадрат кожну відому сторону.або ж залиште ступеня-ви можете звести числа в квадрат пізніше.
- У нашому прикладі напишіть: 9 + b2 = 25.
-
Відокремте невідому сторону на одній стороні рівняння.для цього перенесіть відомі значення на іншу сторону рівняння. Якщо ви знаходите гіпотенузу, то в теоремі Піфагора вона вже відокремлена на одній стороні рівняння (тому робити нічого не потрібно).
- У нашому прикладі перенесіть 9 на праву сторону рівняння, щоб відокремити невідоме b2. Ви отримаєте b2 = 16.
-
Витягніть квадратний корінь з обох частин рівняння. на даному етапі на одній стороні рівняння присутній невідоме (в квадраті), а на іншій стороні — вільний член (число).
- У нашому прикладі b2 = 16. Витягніть квадратний корінь з обох частин рівняння і отримаєте b = 4. Таким чином, другий катет дорівнює4.
-
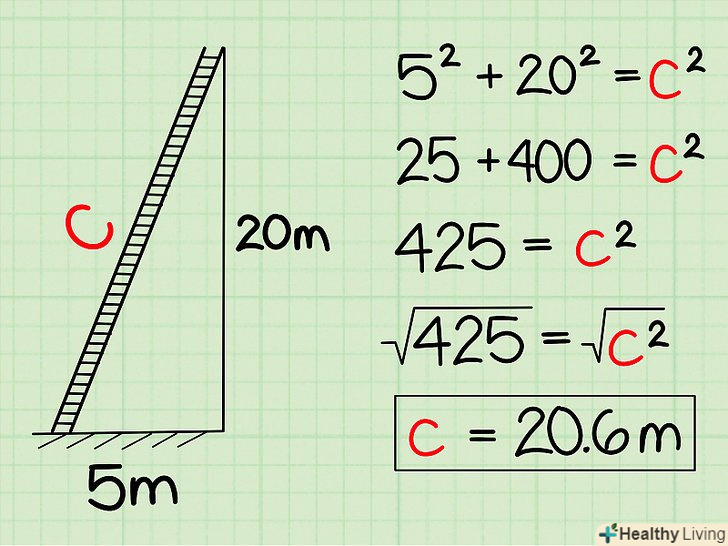
Використовуйте теорему Піфагора в повсякденному житті, так як її можна застосовувати у великій кількості практичних ситуацій. для цього Навчіться розпізнавати прямокутні трикутники в повсякденному житті - в будь-якій ситуації, в якій два предмети (або лінії) перетинаються під прямим кутом, а третій предмет (або лінія) з'єднує (по діагоналі) верхівки двох перших предметів( або ліній), ви можете використовувати теорему Піфагора, щоб знайти невідому сторону (якщо дві інші сторони відомі).
- Приклад: дана сходи, притулена до будівлі. Нижня частина сходів знаходиться в 5 метрах від основи стіни. Верхня частина сходів знаходиться в 20 метрах від землі (вгору по стіні). Яка довжина сходів?
- "в 5 метрах від основи стіни «означає, що а = 5;» знаходиться в 20 метрах від Землі" означає, що b = 20 (тобто вам дані два катети прямокутного трикутника, так як стіна будівлі і поверхня землі перетинаються під прямим кутом). Довжина сходів є довжина гіпотенузи, яка невідома.
- A² + b² = c²
- (5)² + (20)² = c²
- 25 + 400 = c²
- 425 = c²
- С = √425
- С = 20,6. Таким чином, приблизна довжина сходів дорівнює 20,6 метрів.
- "в 5 метрах від основи стіни «означає, що а = 5;» знаходиться в 20 метрах від Землі" означає, що b = 20 (тобто вам дані два катети прямокутного трикутника, так як стіна будівлі і поверхня землі перетинаються під прямим кутом). Довжина сходів є довжина гіпотенузи, яка невідома.
- Приклад: дана сходи, притулена до будівлі. Нижня частина сходів знаходиться в 5 метрах від основи стіни. Верхня частина сходів знаходиться в 20 метрах від землі (вгору по стіні). Яка довжина сходів?
Метод2 З 2:
Обчислення відстані між двома точками на координатній площині
Метод2 З 2:
-
Виберіть дві точки на координатній площині.за теоремою Піфагора можна обчислити довжину відрізка, що з'єднує дві точки на координатній прямій. Для цього необхідно знати координати (х,у) кожної точки.
- Щоб знайти відстань між двома точками, ви будете розглядати точки в якості вершин трикутника, що не прилеглих до прямого кута прямокутного трикутника. Таким чином, ви зможете легко знайти катети трикутника, а потім обчислити гіпотенузу, яка дорівнює відстані між двома точками.
-
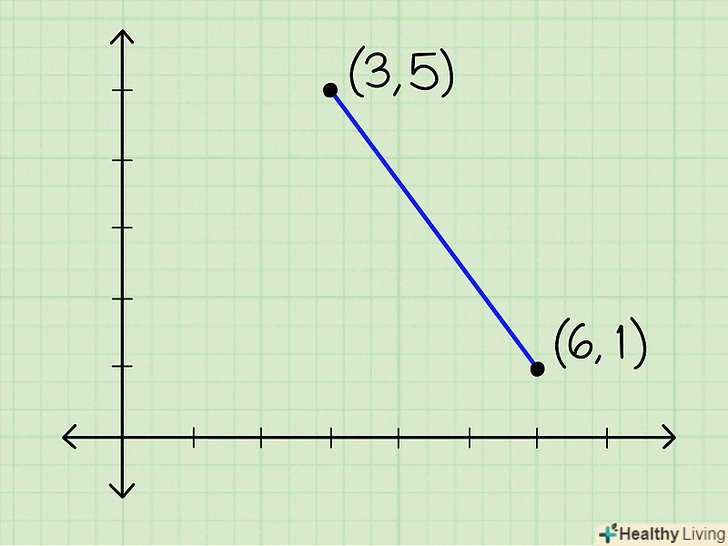
Нанесіть точки на координатну площину. відкладіть координати (х, у), де координата «х» відкладається по горизонтальній осі, а «у» — по вертикальній. Ви можете знайти відстань між точками без побудови графіка, але графік дозволяє візуально представити процес ваших обчислень.
-
Знайдіть катети трикутника. ви можете зробити це, вимірявши довжину катетів безпосередньо на графіку або за допомогою формул: |x1 - x2| для обчислення довжини горизонтального катета, і |y1 - y2| для обчислення довжини вертикального катета, де (x1,y1) – координати першої точки, А (x2,y2) – координати другої точки.
- Приклад: дані точки: а(6,1) і в (3,5). Довжина горизонтального катета:
- |x1 - x2|
- |3 - 6|
- | -3 | =3
- Довжини вертикального катета:
- |y1 - y2|
- |1 - 5|
- | -4 | =4
- Таким чином, в прямокутному трикутнику а = 3 і b = 4.
- Приклад: дані точки: а(6,1) і в (3,5). Довжина горизонтального катета:
-
Використовуйте теорему Піфагора для знаходження гіпотенузи. відстань між двома точками дорівнює гіпотенузі трикутника, дві сторони якого ви тільки що знайшли. Використовуйте теорему Піфагора, щоб знайти гіпотенузу, підставивши в формулу знайдені значення катетів (a і b).
- У нашому прикладі а = 3 і b = 4. Гіпотенуза обчислюється наступним чином:
- (3)²+(4)²= c²
- c= √(9+16)
- c= √(25)
- c= 5. Відстань між точками а(6,1) і в (3,5) дорівнює 5.
- У нашому прикладі а = 3 і b = 4. Гіпотенуза обчислюється наступним чином:
Поради
- Гіпотенуза завжди:
- Лежить навпроти прямого кута;
- Є найдовшою стороною прямокутного трикутника;
- Позначається як " с " в теоремі Піфагора;
- √(х) означає "Квадратний корінь з х".
- Не забувайте перевіряти відповідь. Якщо відповідь здається неправильним, виконайте обчислення знову.
- Ще один момент-найдовша сторона лежить навпроти найбільшого кута, а найкоротша сторона — навпроти найменшого кута.
- Вивчіть числа піфагорової трійки, що утворюють сторони прямокутного трикутника. Найпримітивніша піфагорова трійка - це 3, 4, 5. Так, знаючи довжину двох сторін, третю шукати не доведеться.
- Пам'ятайте, гіпотенуза-завжди найдовша сторона.
- Якщо дано звичайний трикутник (а не прямокутний), то потрібно більше інформації, ніж просто довжини двох сторін.
- Графіки є наочним способом нанесення позначень а, b і С.якщо ви вирішуєте задачу, то в першу чергу побудуйте графік.
- Якщо дана довжина тільки однієї сторони, то теорему Піфагора застосовувати не можна. Спробуйте використовувати тригонометрію (sin, cos, tan).
- Якщо мова йде про завдання з якогось сюжету, можна сміливо припустити, що дерева, стовпи, стіни і так далі утворюють прямий кут з землею, якщо не вказано інше.
