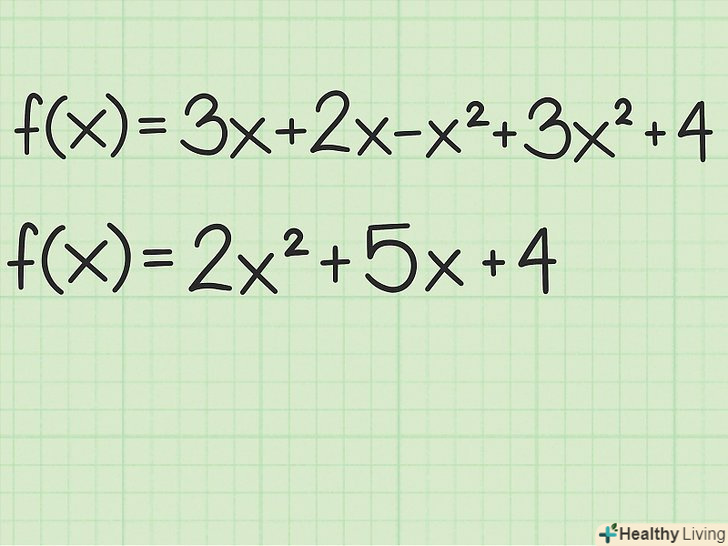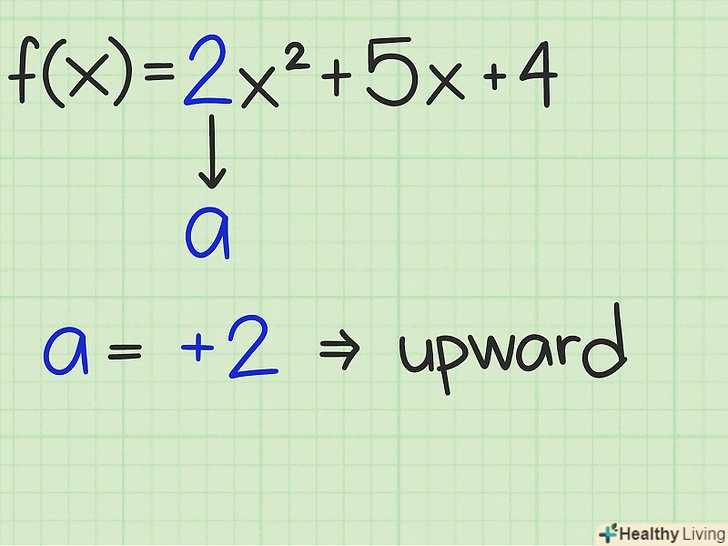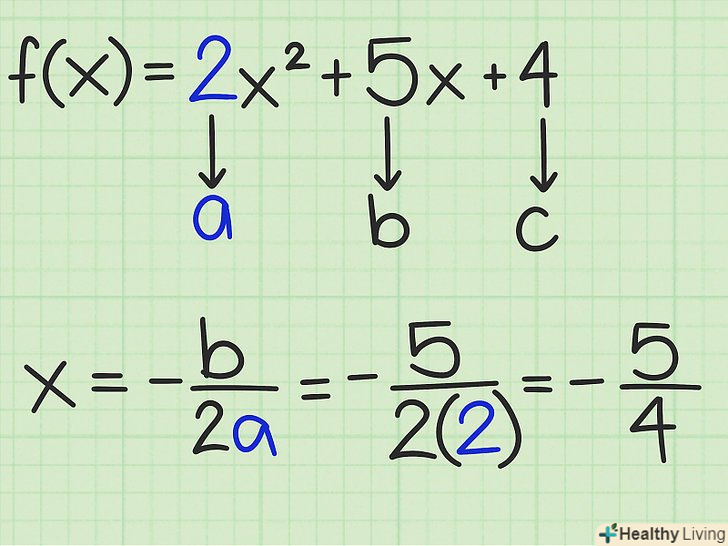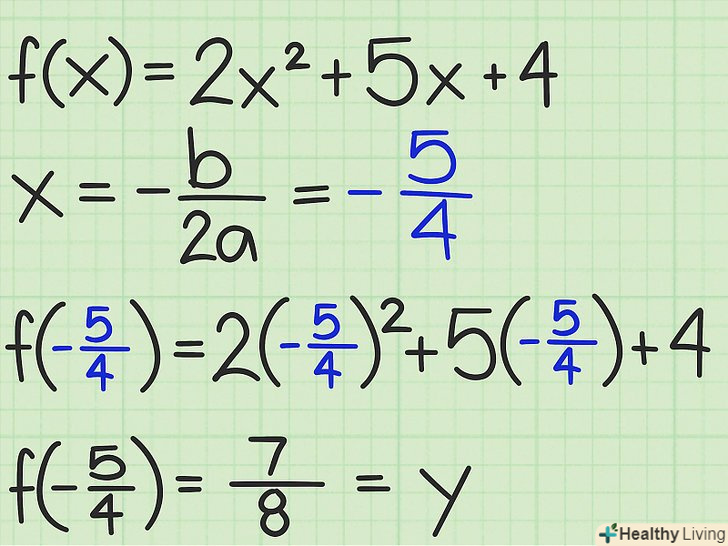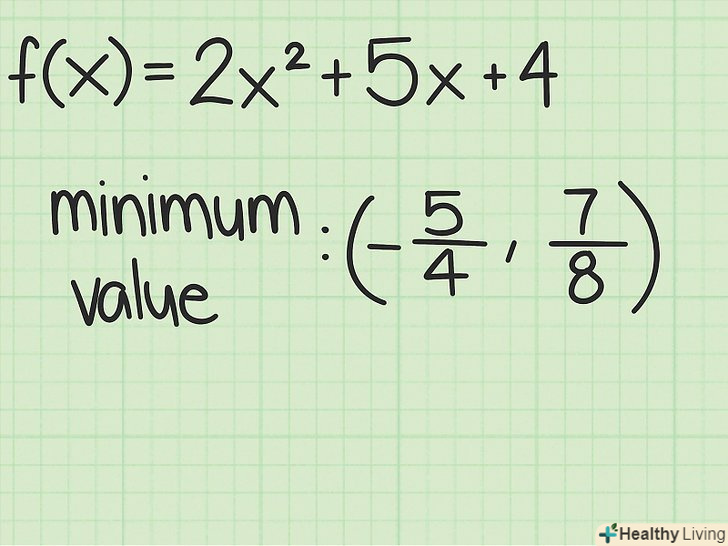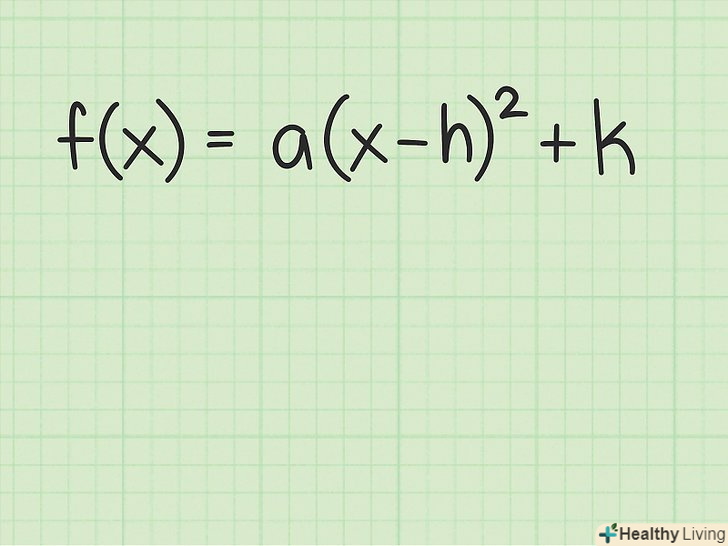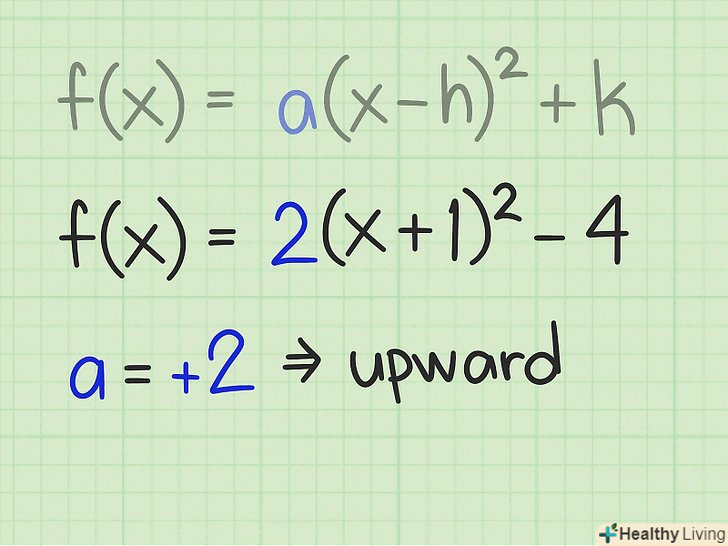У багатьох завданнях потрібно обчислити максимальне або мінімальне значення квадратичної функції. Максимум або мінімум можна знайти, якщо вихідна функція записана в стандартному вигляді: або через координати вершини параболи:
. Більш того, максимум або мінімум будь-якої квадратичної функції можна обчислити за допомогою математичних операцій.
Кроки
Метод1З 3:
Квадратична функція записана в стандартному вигляді
Метод1З 3:
 Запишіть функцію в стандартному вигляді. Квадратична функція - це функція, рівняння якої включає змінну
Запишіть функцію в стандартному вигляді. Квадратична функція - це функція, рівняння якої включає змінну. Рівняння може включати або не включати змінну
. Якщо рівняння включає змінну з показником ступеня більше 2, воно не описує квадратичну функцію. Якщо потрібно, приведіть подібні члени і переставте їх, щоб записати функцію в стандартному вигляді.[1]
- Наприклад, дана функція
. Складіть члени зі змінною
та члени зі змінною
, щоб записати рівняння у стандартному вигляді:
- Наприклад, дана функція
 Визначте напрямок параболи.графік квадратичної функції являє собою параболу. Гілки параболи спрямовані вгору або вниз. Якщо коефіцієнт
Визначте напрямок параболи.графік квадратичної функції являє собою параболу. Гілки параболи спрямовані вгору або вниз. Якщо коефіцієнтпри змінній
позитивний, парабола спрямована вгору. Якщо коефіцієнт
негативний, параболи спрямовані вниз. Наприклад: [2]
. Тут
, тому парабола спрямована вгору.
. Тут
, тому парабола спрямована вниз.
. Тут
, тому парабола спрямована вгору.
- Якщо парабола спрямована вгору, потрібно шукати її мінімум. Якщо парабола спрямована вниз, шукайте її максимум.
 Обчисліть-b/2A. Значення
Обчисліть-b/2A. Значення– це координата
вершини параболи. Якщо квадратична функція записується у стандартному вигляді
, скористайтесь коефіцієнтами при
і
наступним чином:
- У функції
коефіцієнти
і
. Тому координату " x " вершини параболи обчисліть так:
- В якості другого прикладу розглянемо функцію
. Тут
і
. Тому координату " x " вершини параболи обчисліть так:
- У функції
 Знайдіть відповідне значення f(x).підставте знайдене значення " x " у вихідну функцію, щоб знайти відповідне значення f(x). Так ви знайдете мінімум або максимум функції.
Знайдіть відповідне значення f(x).підставте знайдене значення " x " у вихідну функцію, щоб знайти відповідне значення f(x). Так ви знайдете мінімум або максимум функції.- У першому прикладі
ви обчислили, що координата «х» вершини параболи дорівнює
. У вихідній функції замість
підставте
, щоб знайти її максимальне значення:
- У другому прикладі
Ви знайшли, що координата «х» вершини параболи дорівнює
. У вихідній функції замість
підставте
, щоб знайти її максимальне значення:
- У першому прикладі
 Запишіть відповідь.Перечитайте умову задачі. Якщо потрібно знайти координати вершини параболи, у відповіді запишіть обидва значення
Запишіть відповідь.Перечитайте умову задачі. Якщо потрібно знайти координати вершини параболи, у відповіді запишіть обидва значенняі
або
). Якщо необхідно обчислити максимум або мінімум функції, у відповіді запишіть тільки значення
(або
). Ще раз подивіться на знак коефіцієнта
, щоб перевірити, що ви вирахували: максимум або мінімум.
- У першому прикладі
значення
позитивне, тому ви вирахували мінімум. Вершина параболи лежить в точці з координатами
, мінімальне значення функції дорівнює
.
- У другому прикладі
значення
негативне, тому ви знайшли максимум. Вершина параболи лежить в точці з координатами
, а максимальне значення функції дорівнює
.
- У першому прикладі
Метод2 З 3:
Квадратична функція записана через координати вершини параболи
Метод2 З 3:
 Запишіть квадратичну функцію через координати вершини параболи. таке рівняння має такий вигляд:[3]
Запишіть квадратичну функцію через координати вершини параболи. таке рівняння має такий вигляд:[3]- Якщо функція вже записана в такому вигляді, просто знайдіть значення коефіцієнтів
,
і
. Якщо функція дана в стандартному вигляді
, доповніть її до повного квадрата і запишіть через координати вершини параболи.
- Щоб дізнатися, як доповнювати до повного квадрата, прочитайте цю статтю.
 Визначте напрямок параболи. для цього подивіться на знак коефіцієнта
Визначте напрямок параболи. для цього подивіться на знак коефіцієнта. Якщо коефіцієнт
позитивний, парабола спрямована вгору. Якщо коефіцієнт
негативний, параболи спрямовані вниз. Наприклад: [4]
. Тут
, тобто коефіцієнт позитивний, тому парабола спрямована вгору.