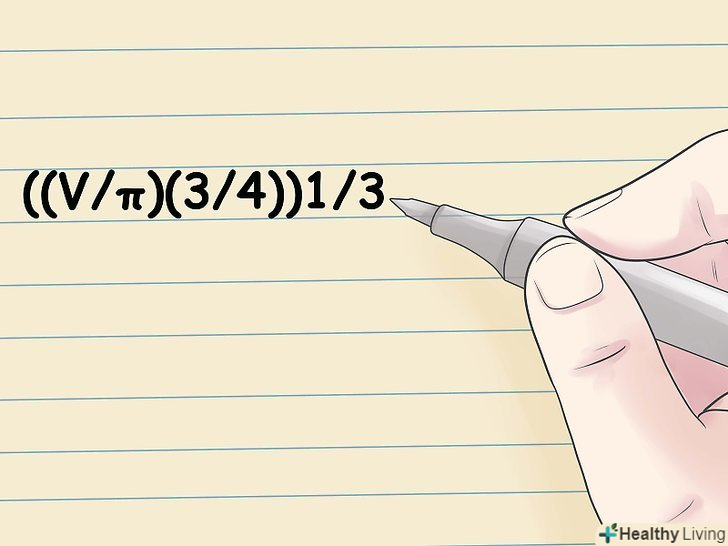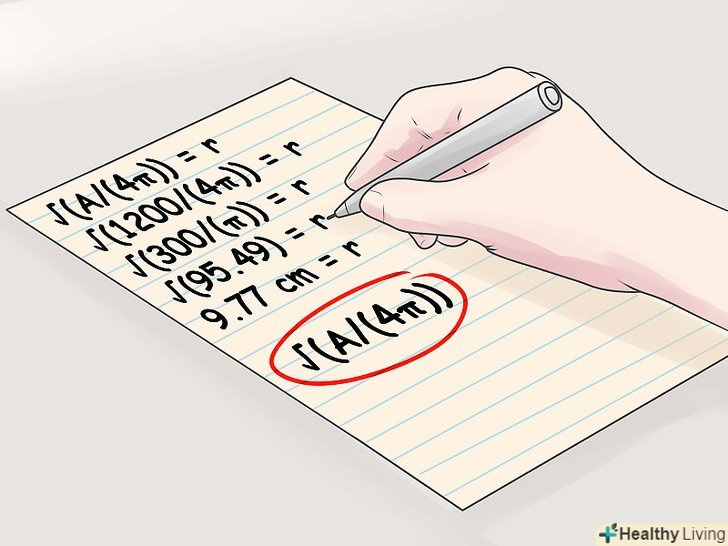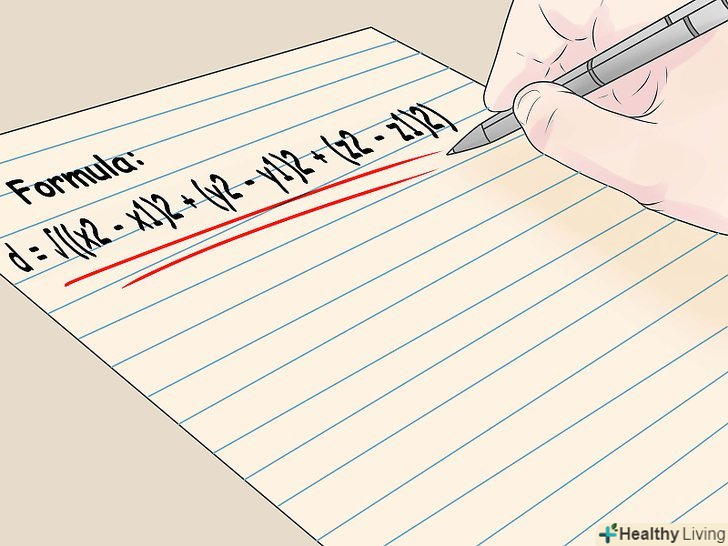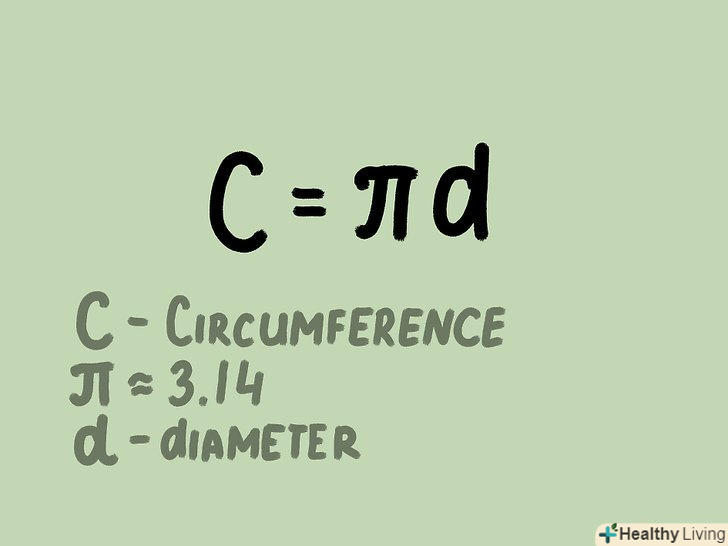1. Головна
    2. Геометрія
    3. Як знайти радіус кулі-

Як знайти радіус кулі-

Радіус кулі (позначається як r або R) – це відрізок, який з'єднує центр кулі з будь-якою точкою на його поверхні. Як і у випадку кола, радіус кулі є важливою величиною, яка необхідна для знаходження діаметра кулі, довжини кола, площі поверхні і/або обсягу. Але радіус кулі можна знайти і за даним значенням діаметра, довжини кола та іншої величини. Використовуйте формулу, в яку можна підставити дані значення.

Метод1З 3:
Формули для обчислення радіуса

  1. Обчисліть радіус по діаметру.радіус дорівнює половині діаметра, тому використовуйте формулу Г = D / 2. Ця така ж формула, яка використовується при обчисленні радіуса і діаметра кола.[1]
    • Наприклад, дано куля з діаметром 16 см.радіус цієї кулі: r = 16/2 =8 см. Якщо діаметр дорівнює 42 см, то радіус дорівнює 21 см (42/2=21).
  2. Обчисліть радіус по довжині кола.використовуйте формулу: R = C / 2π. Так як довжина кола C = πD = 2πR, то розділіть формулу для обчислення довжини кола на 2π і отримаєте формулу для знаходження радіуса.[2]
    • Наприклад, дано куля з довжиною кола 20 см.радіус цієї кулі:R = 20/2π = 3,183 см.
    • Така ж формула використовується при обчисленні радіуса і довжини кола кола.
  3. Обчисліть радіус за обсягом кулі. використовуйте формулу:R = ((V/π)(3/4))1/3 .[3] Об'єм кулі обчислюється за формулою V = (4/3) πr3. Відокремивши r на одній стороні рівняння, ви отримаєте формулу ((V/π)(3/4))3 = г, тобто для обчислення радіуса обсяг кулі ділимо на π, результат множимо на 3/4, а отриманий результат зводимо в ступінь 1/3 (або витягуємо кубічний корінь).[4]
    • Наприклад, дана куля з об'ємом 100 см3. Радіус цієї кулі обчислюється так:
      • ((V/π)(3/4))1/3 = r
      • ((100/π)(3/4))1/3 = r
      • ((31,83)(3/4))1/3 = r
      • (23,87)1/3 = r
      • 2,88 см = r
  4. Обчисліть радіус по площі поверхні. використовуйте формулу: Г = √(A/(4 π)). Площа поверхні кулі обчислюється за формулою а = 4πr2. Відокремивши r на одній стороні рівняння, ви отримаєте формулу √(A/(4π)) = r, тобто, щоб обчислити радіус, потрібно витягти квадратний корінь з площі поверхні, поділеної на 4π. Замість того щоб витягувати корінь, вираз (A/(4π)) можна звести в ступінь 1/2.[5]
    • Наприклад, дана куля з площею поверхні 1200 см3. Радіус цієї кулі обчислюється так:
      • √(A/(4π)) = r
      • √(1200/(4π)) = r
      • √(300/(π)) = r
      • √(95,49) = r
      • 9,77 см = r

Метод2 З 3:
Визначення основних величин

  1. Запам'ятайте основні величини, які мають відношення до обчислення радіуса кулі.радіус кулі-це відрізок, який з'єднує центр кулі з будь-якою точкою на його поверхні. Радіус кулі можна обчислити за даними значенням діаметра, довжини кола, обсягу або площі поверхні.
    • Діаметр (D) - це відрізок, який з'єднує дві точки на поверхні кулі і проходить через його центр (тобто це найбільша відстань між протилежними точками, що лежать на поверхні кулі). Діаметр дорівнює подвоєному радіусу.
    • Довжина кола (С) являє собою довжину кола великого кола, тобто кола, який утворює січна площина, що проходить через центр кулі.
    • Обсяг (V) – це значення тривимірного простору, займаного кулею.[6]
    • Площа поверхні (А) – це значення двовимірного (плоского) простору, обмеженого поверхнею кулі.
    • Пі (π) – це постійна, яка дорівнює відношенню довжини кола до її діаметру. Першими десятьма цифрами цієї постійної є 3,141592653, але найчастіше число Пі округляється до 3,14.
  2. Скористайтеся значеннями даних величин, щоб знайти радіус.радіус можна обчислити за даними значенням діаметра, довжини кола, обсягу і площі поверхні. Більш того, зазначені величини можна знайти за даним значенням радіуса. Щоб обчислити радіус, просто Перетворіть формули для знаходження зазначених величин. Нижче наведені формули (в яких присутній радіус) для обчислення діаметра, довжини кола, обсягу і площі поверхні.
    • D = 2г. Як і у випадку кола, діаметр кулі в два рази більше його радіуса.
    • C = πD = 2πr. Як і у випадку кола, довжина кола кулі дорівнює добутку π на діаметр кулі. Так як діаметр вдвічі більше радіуса, то довжина кола кулі дорівнює подвоєному добутку π на радіус кулі.
    • V = (4/3)πr3. Обсяг кулі дорівнює добутку 4/3 на π і на радіус в кубі.[7]
    • А = 4πr2. Площа поверхні кулі дорівнює учетверенному добутку π на радіус в квадраті. Так як площа кола дорівнює πr2, то площа поверхні кулі в чотири рази більше площі кола, який утворює січна площина, що проходить через центр кулі.

Метод3 З 3:
Знаходження радіуса по відстані між двома точками

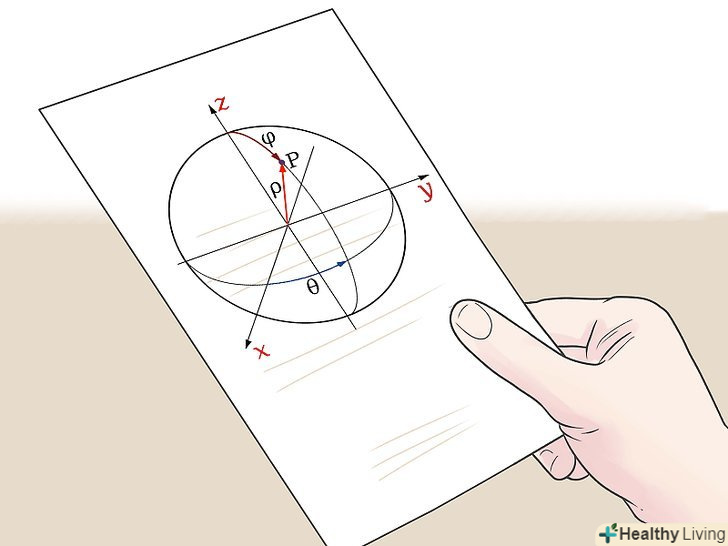
  1. Знайдіть координати (х,у,z) центру кулі.радіус кулі дорівнює відстані між його центром і будь-якою точкою, що лежить на поверхні кулі. Якщо відомі координати центру кулі і будь-якої точки, що лежить на його поверхні, можна знайти радіус кулі за спеціальною формулою, обчисливши відстань між двома точками. Спочатку знайдіть координати центру кулі. Майте на увазі, що так як куля є тривимірною фігурою, то точка буде мати три координати (х,у,z), а не дві (х,у).
    • Розглянемо приклад. Дана куля з центром з координатами(4,-1,12). Скористайтеся цими координатами, щоб знайти радіус кулі.
  2. Знайдіть координати точки, що лежить на поверхні кулі. Тепер потрібно знайти координати (х,у,z) будь точки, що лежить на поверхні кулі. Так як всі точки, що лежать на поверхні кулі, розташовані на однаковій відстані від центру кулі, для обчислення радіусу кулі можна вибрати будь-яку точку.
    • У нашому прикладі припустимо, що деяка точка, що лежить на поверхні кулі, має координати(3,3,0). Обчисливши відстань між цією точкою і центром кулі, ви знайдете радіус.
  3. Обчисліть радіус за формулою d = √((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2).дізнавшись координати центру кулі і точки, що лежить на його поверхні, ви можете знайти відстань між ними, яке дорівнює радіусу кулі. Відстань між двома точками обчислюється за формулою d = √((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2), де d – відстань між точками, (x1,y1,z1) – координати центра кулі, (x2,y2,z2) – координати точки, що лежить на поверхні кулі.
    • У розглянутому прикладі замість (x1,y1,z1) підставте (4, -1,12), а замість (x2, y2, z2) підставте (3,3,0):
      • D = √((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2)
      • D = √((3 - 4)2 + (3 - -1)2 + (0 - 12)2)
      • D = √((-1)2 + (4)2 + (-12)2)
      • D = √(1 + 16 + 144)
      • D = √(161)
      • D = 12,69. Це шуканий радіус кулі.
  4. Майте на увазі, що в загальних випадках r = √((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). всі точки, що лежать на поверхні кулі, розташовані на однаковій відстані від центру кулі. Якщо у формулі для знаходження відстані між двома точками " d "замінити на" r", вийде формула для обчислення радіусу кулі по відомим координатам (x1,y1,z1) центру кулі і координатам (x2,y2,z2) будь-якої точки, що лежить на поверхні кулі.
    • Піднесіть обидві сторони цього рівняння у квадрат, і отримаєте r2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2. Зауважте, що це рівняння відповідає рівнянню сфери r2 = x2 + y2 + z2 з центром з координатами (0,0,0).

Поради

  • Не забувайте про порядок виконання математичних операцій. Якщо ви не пам'ятаєте цей порядок, а ваш калькулятор вміє працювати з круглими дужками, користуйтеся ними.
  • У цій статті розповідається про обчислення радіуса кулі. Але якщо ви відчуваєте труднощі з вивченням геометрії, краще почати з обчислення величин, пов'язаних з кулею, через відоме значення радіуса.
  • Π – Пі) - це буква грецького алфавіту, яка позначає постійну, рівну відношенню діаметра кола до довжини його кола. Число Пі є ірраціональним числом, яке не записується як відношення дійсних чисел. Існує безліч наближень, наприклад, відношення 333/106 дозволить знайти число Пі з точністю до чотирьох цифр після десяткової коми. Як правило, користуються приблизним значенням числа Пі, яке дорівнює 3,14.

Схожі статті

Джерела

  1. ↑ Http://www.rkm.com.au/CALCULATORS/CALCULATOR-circle-sphere.html
  2. ↑ Http://www.calculatorsoup.com/calculators/geometry-solids/sphere.php
  3. ↑ Http://www.varsitytutors.com/sat_math-help/how-to-find-the-radius-of-a-sphere
  4. ↑ Http://mathcentral.uregina.ca/QQ/database/QQ.09.07/h/cey2.html
  5. ↑ Http://formulas.tutorvista.com/math/sphere-formula.html
  6. ↑ Http://www.web-formulas.com/Math_Formulas/Geometry_Volume_of_Sphere.aspx
  7. ↑ Http://mathforum.org/library/drmath/view/54892.html

Ще почитати: