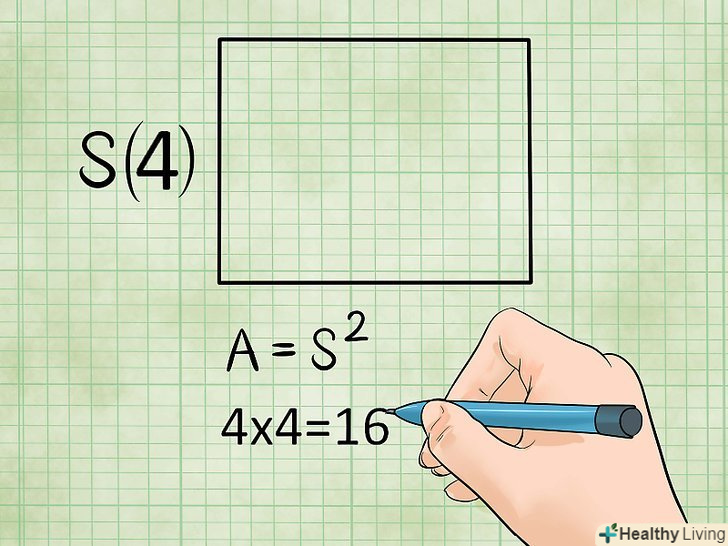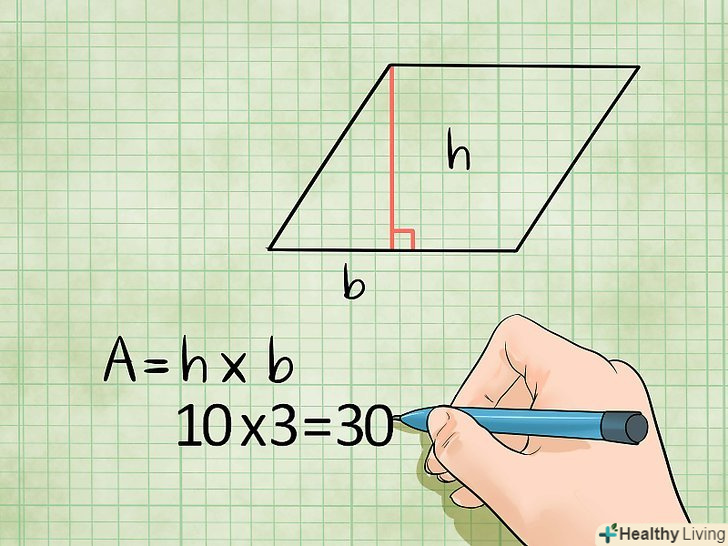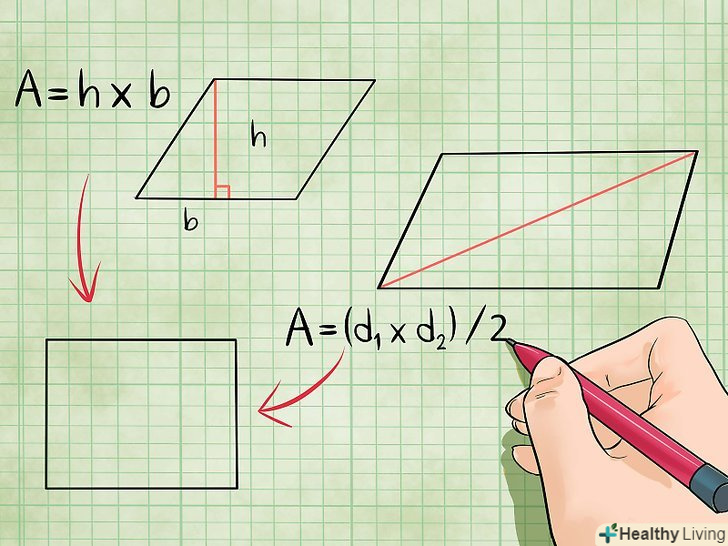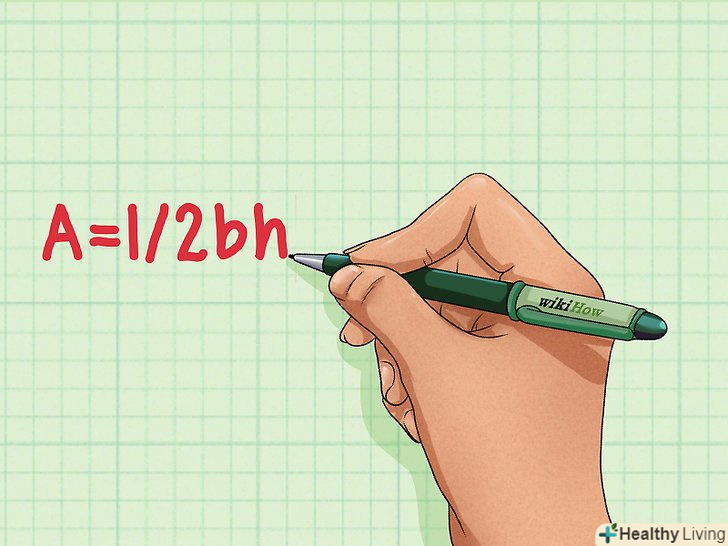1. Головна
    2. Геометрія
    3. Як знайти площу чотирикутника-

Як знайти площу чотирикутника-

Вам дана задача, в якій потрібно знайти площу чотирикутника, а ви навіть не знаєте, що таке чотирикутник? Не хвилюйтеся, ця стаття вам допоможе! Чотирикутник-це будь-яка фігура з чотирма сторонами. Для обчислення площі чотирикутника потрібно визначити тип чотирикутника, який вам дано, і скористатися відповідною формулою.

Метод1З 4:
Квадрат, прямокутник та інші паралелограми

  1. Визначення паралелограма.паралелограм - це чотирикутник, у якого протилежні сторони рівні і паралельні один одному. Квадрати, прямокутники і ромби — це паралелограми.
    • Квадрат - це паралелограм, у якого всі сторони рівні і перетинаються під прямим кутом.
    • Прямокутник-це паралелограм, у якого всі сторони перетинаються під прямим кутом.
    • Ромб-це паралелограм, у якого всі сторони рівні.
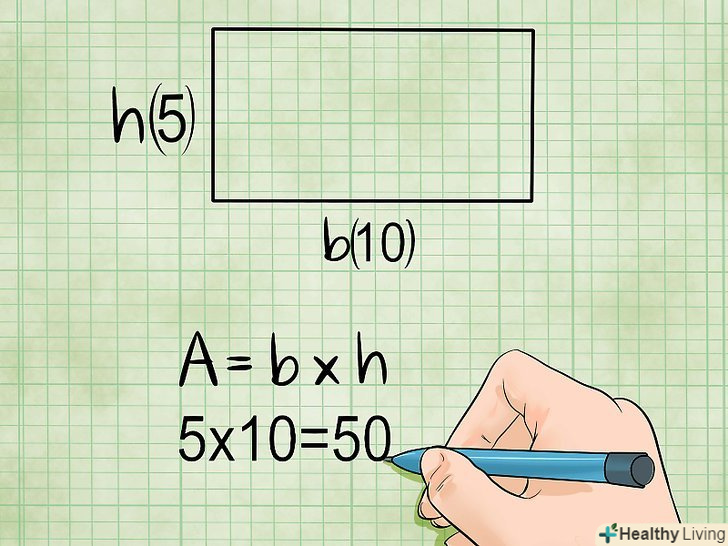
  2. Площа прямокутника.щоб обчислити площу прямокутника, потрібно знати його ширину (коротка сторона; уявіть її як висоту) і довжину (довга сторона; уявіть її як сторону, до якої проведена висота). Площа прямокутника дорівнює добутку довжини на ширину.
    • ' Площа = довжина х висота, або S = a х h.
    • Приклад: якщо довжина прямокутника дорівнює 10 см, а ширина дорівнює 5 см, то площа цього прямокутника: S = 10 х 5 =50 квадратних сантиметрів .
    • Не забувайте, що площа вимірюється в квадратних одиницях (квадратних метрах, квадратних сантиметрах і так далі).
  3. Площа квадрата. Квадрат-це окремий випадок прямокутника, тому використовуйте ту ж формулу, що і для знаходження площі прямокутника. Але в квадраті всі сторони рівні, тому площа квадрата дорівнює будь-який з його сторін, зведеної в квадрат (тобто помноженої саму на себе).[1]
    • Площа = сторона х сторона, або S = a2.
    • Приклад: якщо сторона квадрата дорівнює 4 см (a = 4), то площа цього квадрата: S = a2 = 4 х 4 = 16 квадратних сантиметрів.
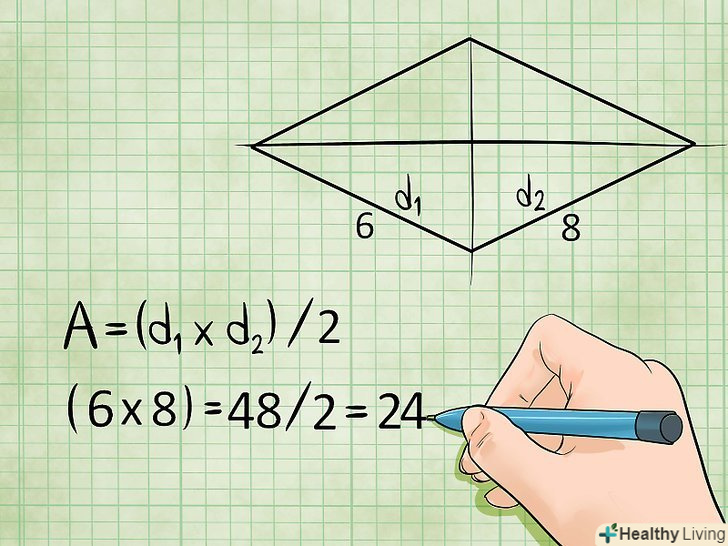
  4. Площа ромба дорівнює добутку його діагоналей, розділеної на два.діагоналі - це відрізки, що з'єднують протилежні вершини ромба.[2]
    • Площа = (діагональ1 х діагональ2)/2, або S = (d1 x d2)/2
    • Приклад: якщо діагоналі ромба рівні 6 см і 8 см, то площа цього ромба: S = (6 х 8)/2 = 24 квадратних сантиметрів.
  5. Площа ромба також можна знайти, якщо помножити його сторону на висоту, опущену на цю сторону.але не плутайте висоту з суміжною стороною. Висота-це пряма, опущена з будь-якої вершини ромба на протилежну сторону, і перетинає протилежну сторону під прямим кутом.
    • Якщо довжина ромба дорівнює 10 см, а його висота дорівнює 3 см, то площа такого ромба дорівнює 10 х 3 = 30 квадратних сантиметрів.
  6. Формули для обчислення площ ромба і прямокутника застосовні до квадратів, так як квадрат — це окремий випадок як прямокутника, так і ромба.
    • Площа = сторона х висоту, або S = a х
    • Площа = (діагональ1 x діагональ2)/2, або S = (d1 x d2)/2
    • Приклад: якщо сторона квадрата дорівнює 4 см, то його площа дорівнює 4 х 4 = 16 квадратних сантиметрів.
    • Приклад: діагоналі квадрата рівні по 10 см.ви можете знайти площу цього квадрата за формулою: (10 х 10)/2 = 100/2 = 50 квадратних сантиметрів.

Метод2З 4:
Трапеція

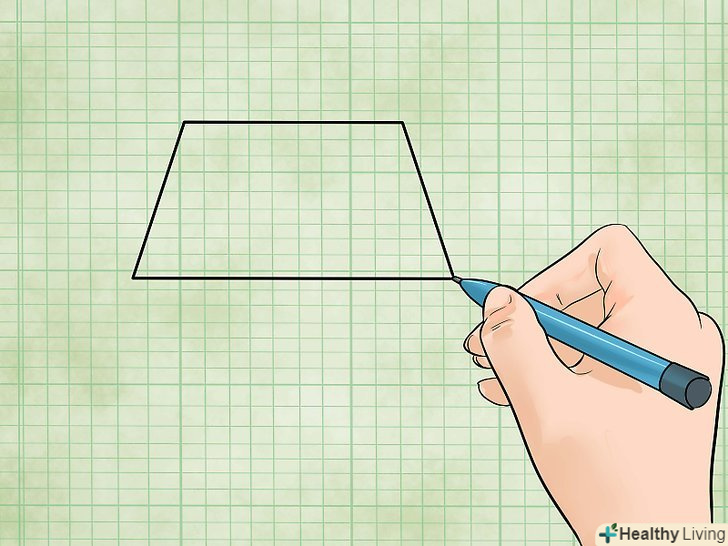
  1. Визначення трапеції.трапеція - це чотирикутник, у якого дві протилежні сторони паралельні один одному. Кожна з чотирьох сторін трапеції може бути різної довжини.
    • Є два способи обчислення площі трапеції (в залежності від даних значень).
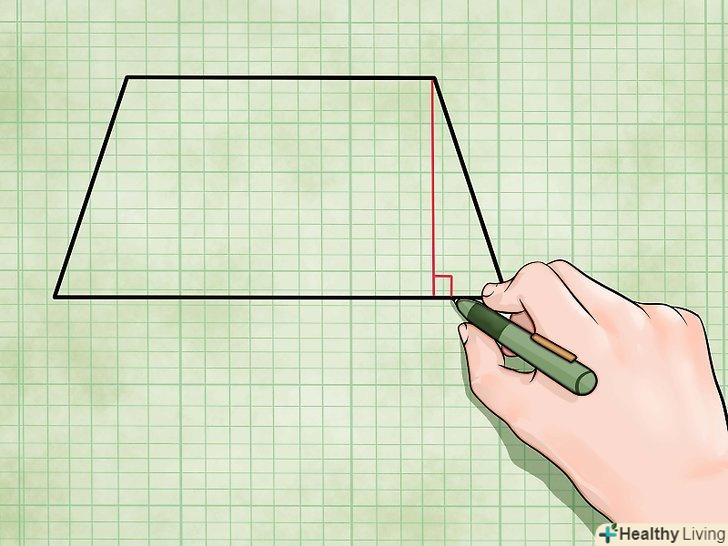
  2. Знайдіть висоту трапеції.Висота трапеції-відрізок, що з'єднує паралельні сторони (підстави) і перетинає їх під прямим кутом (висота не дорівнює бічним сторонам). Ось як знайти висоту трапеції:[3]
    • З точки перетину меншого підстави і бічної сторони проведіть перпендикуляр до більшого підстави. Цей перпендикуляр і є висота трапеції.
    • Щоб обчислити висоту, використовуйтетригонометрію. Наприклад, якщо ви знаєте бічну сторону і прилеглий до неї кут, то висота дорівнює добутку бічної сторони на синус прилеглого кута.
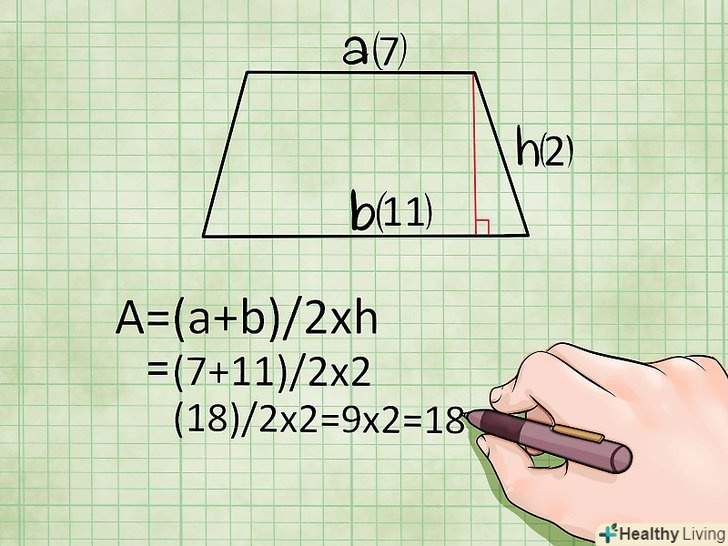
  3. Знайдіть площу трапеції, використовуючи висоту.якщо ви знаєте висоту трапеції і обидві підстави, використовуйте наступну формулу для обчислення площі трапеції:
    • Площа = (основание1 + основание2)/2 × висота, або S = (a+b)/2 × h
    • Приклад: якщо висота трапеції дорівнює 2 см, а підстави трапеції рівні 7 см і 11 см, то площа цієї трапеції: S = (a+b)/2 * h = (7 + 11)/2 * 2 = 18 квадратних сантиметрів.
    • Якщо висота трапеції дорівнює 10, а підстави трапеції рівні 7 і 9, то площа цієї трапеції: S = (a+b)/2 * h = (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80.
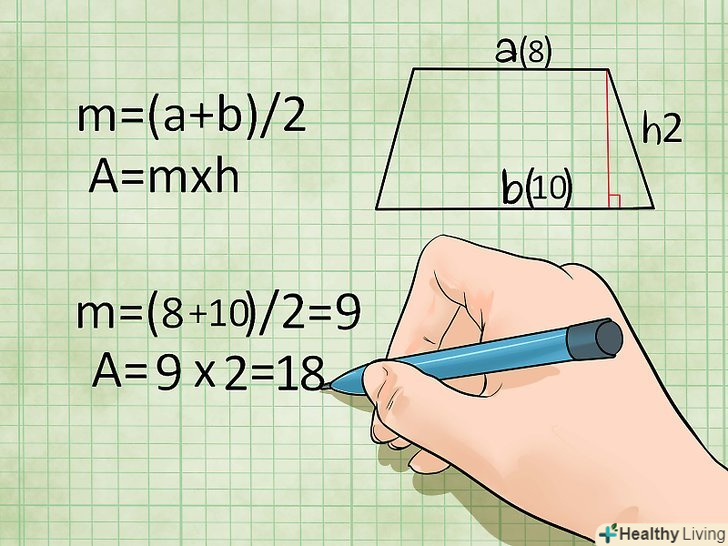
  4. Знайдіть площу трапеції, використовуючи середню лінію. середня лінія-це відрізок, паралельний підстав і ділить бічні сторони навпіл. Середня лінія дорівнює середньому значенню від обох підстав (a і b): середня лінія = (a+b)/2.
    • Площа = середня лінія х висота, або S = m х
    • По суті, тут ви використовуєте формулу для знаходження площі трапеції по двох підставах, але замість (a+b)/2 підставлена m (середня лінія).
    • Приклад: якщо середня лінія трапеції дорівнює 9 см, то площа цієї трапеції: S = m * h = 9 х 2 = 18 квадратних сантиметрів (ви отримали ту ж відповідь, що і в попередньому кроці).

Метод3З 4:
Дельтоид

  1. Визначення дельтоїда.Дельтоїд-це чотирикутник з двома парами сторін однакової довжини.
    • Є два способи обчислення площі дельтоїда (в залежності від даних значень).
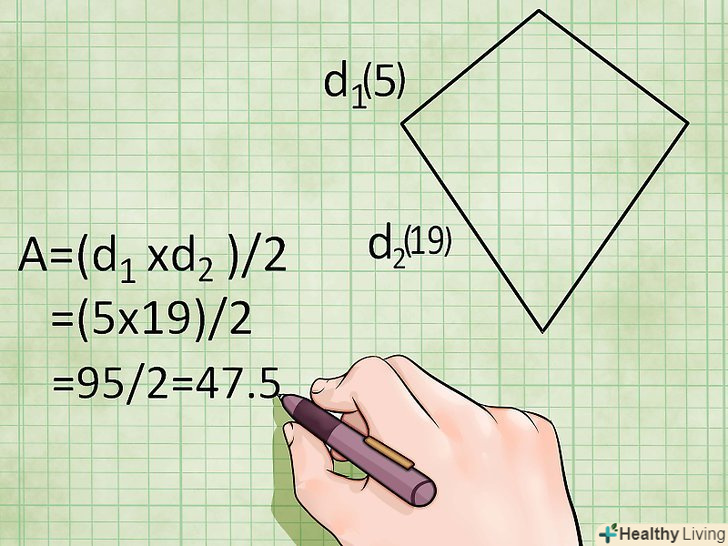
  2. Знайдіть площу дельтоїда, використовуючи формулу для знаходження площі ромба (з використанням діагоналей), так як ромб — це окремий випадок дельтоїда, у якого всі сторони рівні.нагадаємо, що діагональ-відрізок, що з'єднує протилежні вершини.
    • Площа = (діагональ1 х діагональ2)/2, або S = (d1 x d2)/2
    • Приклад: якщо діагоналі дельтоїда рівні 19 см і 5 см, то площа цього дельтоїда: S = (19 х 5)/2 = 47,5 квадратних сантиметрів.
    • Якщо ви не знаєте довжини діагоналей і не можете їх виміряти, використовуйте тригонометрію, щоб обчислити їх. Прочитайтецю статтю, щоб дізнатися більше інформації.
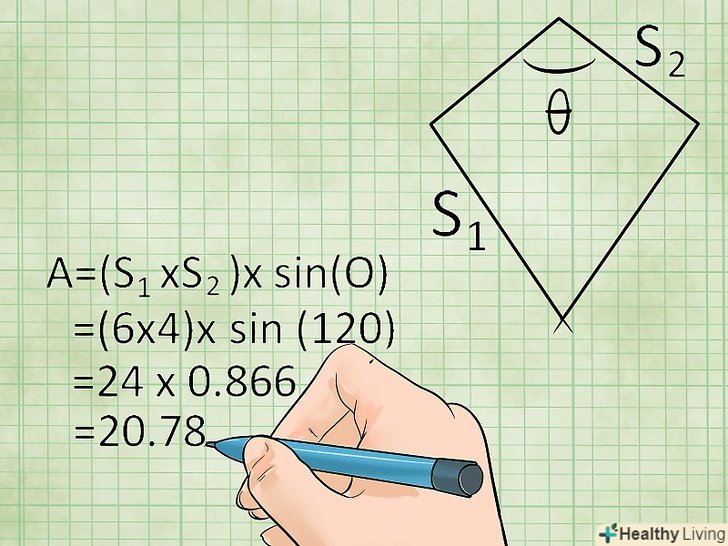
  3. Знайдіть площу дельтоїда, використовуючи нерівні сторони і кут між ними. якщо ви знаєте нерівні сторони і кут між цими сторонами (θ), то площа дельтоїда обчислюється за допомогою тригонометрії за формулою:[4]
    • Площа = (сторона1 х сторона2) х sin (кут), або S = (a × b) × sin(θ), де θ — кут між нерівними сторонами.
    • Приклад: якщо сторони дельтоїда рівні 4 см і 6 см, а кут між ними дорівнює 120 градусам, то площа дельтоїда дорівнює (6 х 4) х 120 = 24 х 0,866 = 20,78 квадратних сантиметрів.
    • Зверніть увагу, що ви повинні використовувати дві нерівні сторони і кут між ними; якщо ви використовуєте дві рівні сторони і кут між ними, Ви отримаєте неправильну відповідь.

Метод4З 4:
Чотирикутник довільної форми

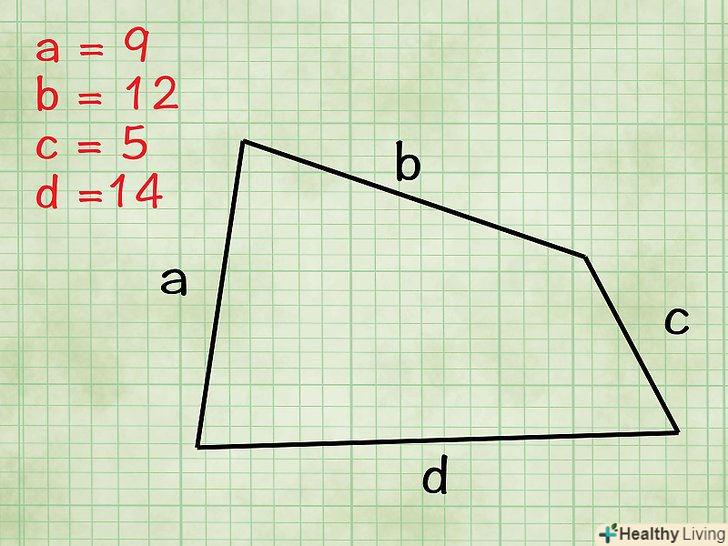
  1. Якщо вам дано чотирикутник довільної форми, то навіть для таких чотирикутників існують формули для обчислення їх площ. зверніть увагу, що такі формули вимагають знання тригонометрії.
    • По-перше, знайдіть довжини всіх чотирьох сторін. Позначимо їх через a, b, c, d( Анавпроти з, а bнавпроти d).
    • Приклад: дано чотирикутник довільної форми зі сторонами 12 см, 9 см, 5 см і 14 см.
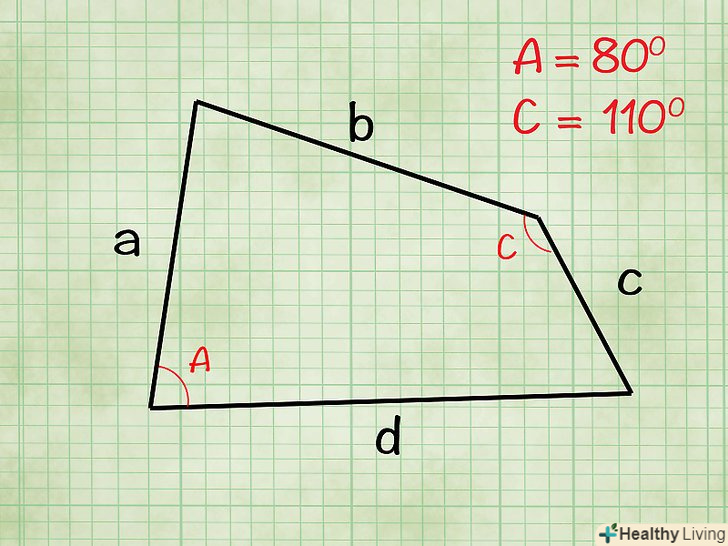
  2. Знайдіть кут а між сторонами а і d і кут С між сторонами b і с (Ви можете знайти будь-які два протилежних кута).
    • У нашому чотирикутнику А = 80 градусів і C = 110 градусів.
  3. Уявіть, що існує відрізок, що з'єднує вершини, утворені сторонами а і b і сторонами с і D. цей відрізок розділить чотирикутник на два трикутника. Так як Площа трикутника дорівнює 1 / 2absinc, де C — Кут між сторонами a і b, ви можете знайти площі двох трикутників і скласти їх, щоб обчислити площу квадрата.
    • Площа = 0,5 х сторона1 х сторона4 х sin(кут між стороной1 і стороной4) + 0,5 х сторона2 х сторона3 х sin (кут між стороной2 і стороной3), або
    • Площа = 0,5 a × d × sin A + 0,5 × b × c × sin C
    • Приклад: Ви знайшли сторони і кути, тому просто підставте їх у формулу.
      = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
      = 84 × sin (80) + 22,5 × sin (110)
      = 84 × 0,984 + 22,5 × 0,939
      = 82,66 + 21,13 = 103,79 квадратних сантиметрів.
    • Зверніть увагу, що якщо ви намагаєтеся знайти площу паралелограма (у якого протилежні кути рівні), то формула набуде вигляду: Площа = 0.5 * (ad + bc) * sin a

Поради


Джерела

  1. ↑ Http://www.dummies.com/how-to/content/how-to-calculate-the-area-of-a-quadrilateral.html
  2. ↑ Http://www.mathopenref.com/rhombusarea.html
  3. ↑ Http://www.mathgoodies.com/lessons/vol1/area_trapezoid.html
  4. ↑ Http://www.mathopenref.com/kitearea.html
  5. ↑ Http://www.handymath.com/cgi-bin/irregangle12.cgi?submit=Entry

Ще почитати: