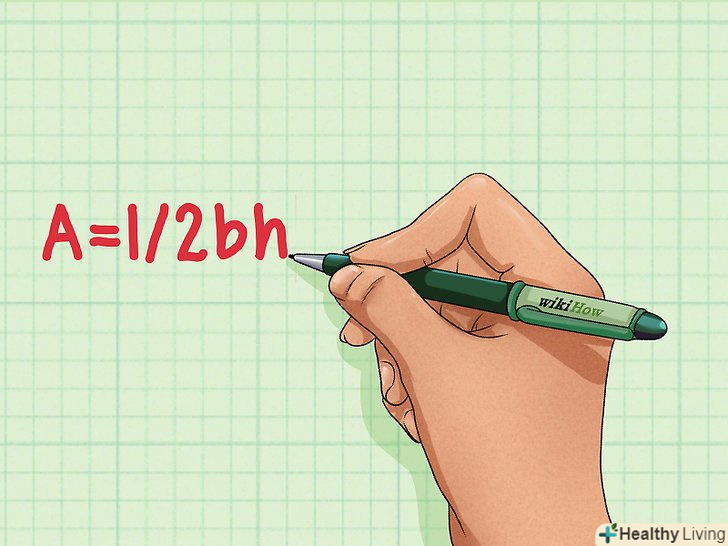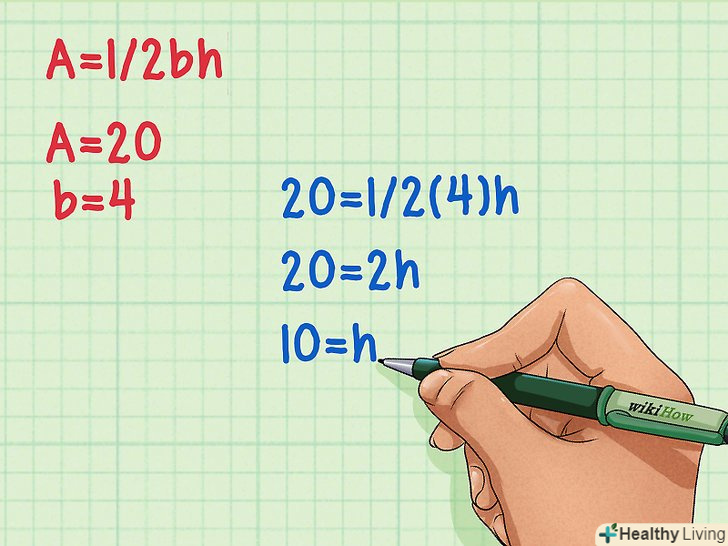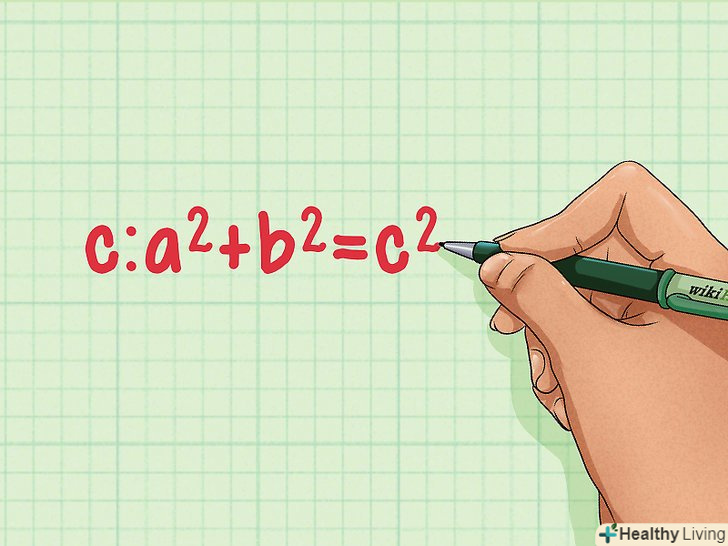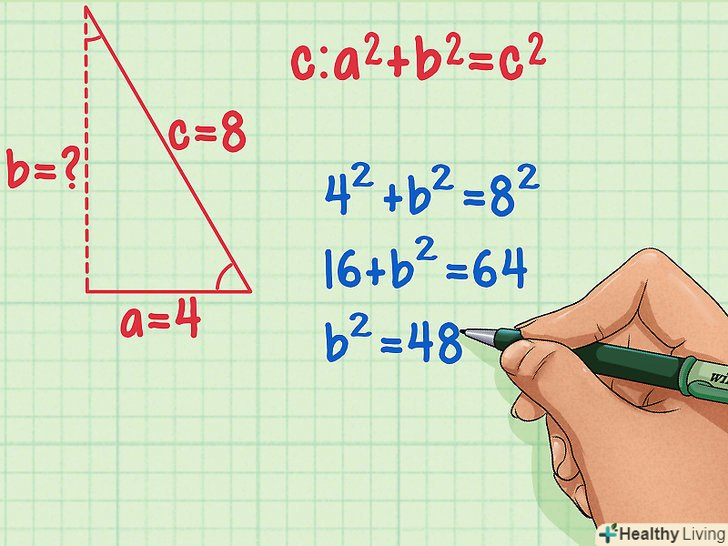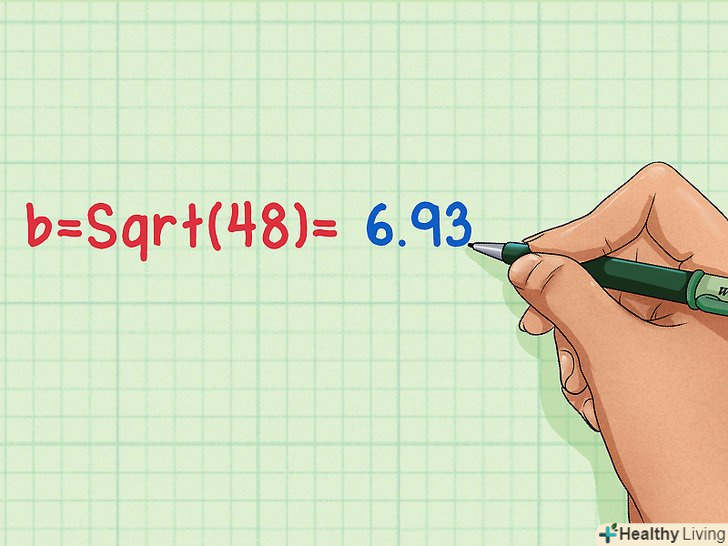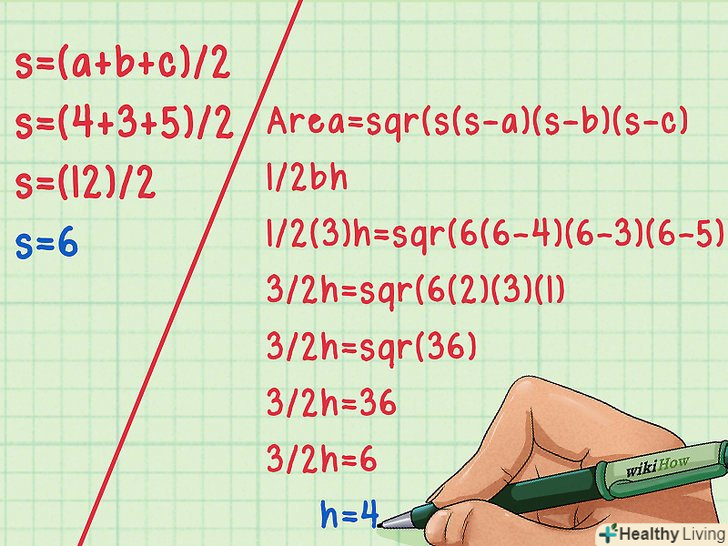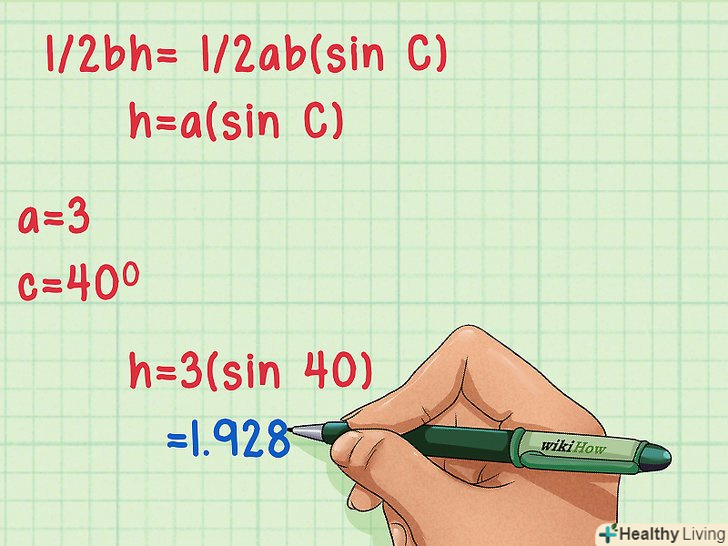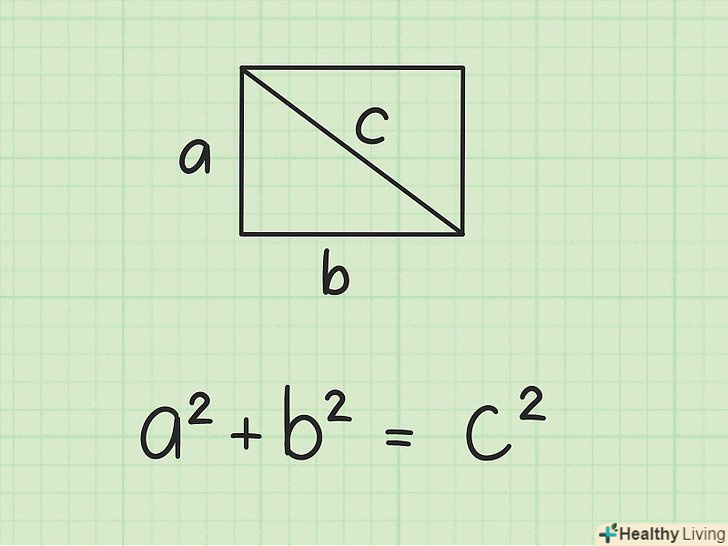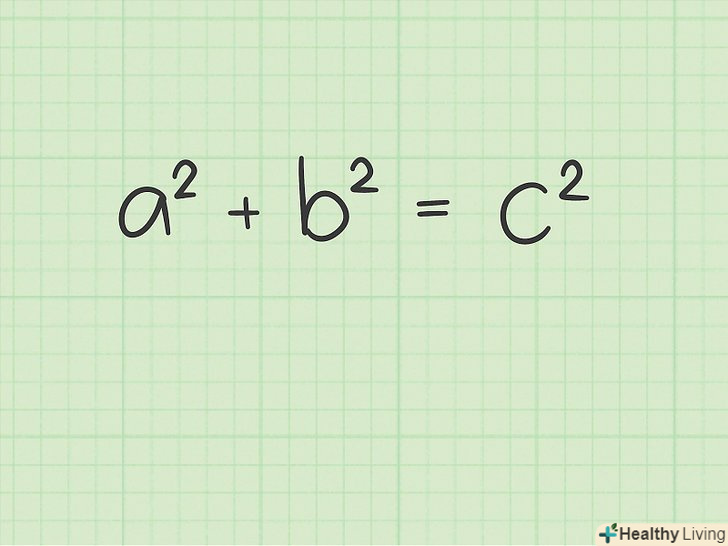1. Головна
    2. Геометрія
    3. Як знайти висоту трикутника

Як знайти висоту трикутника

Для обчислення площі трикутника вам необхідно знати його висоту. Якщо вона не дана, ви можете обчислити її по відомим вам величинам! У цій статті ми розповімо про декілька способів знайти висоту трикутника по відомим значенням інших величин.

Метод1З 3:
Як знайти висоту по підставі і площі

  1. Нагадаємо формулу для обчислення площі трикутника.площа трикутника обчислюється за формулою:A = 1/2BH.[1]
    • А-площа трикутника
    • B-сторона трикутника, на яку опущена висота.
    • H-висота трикутника
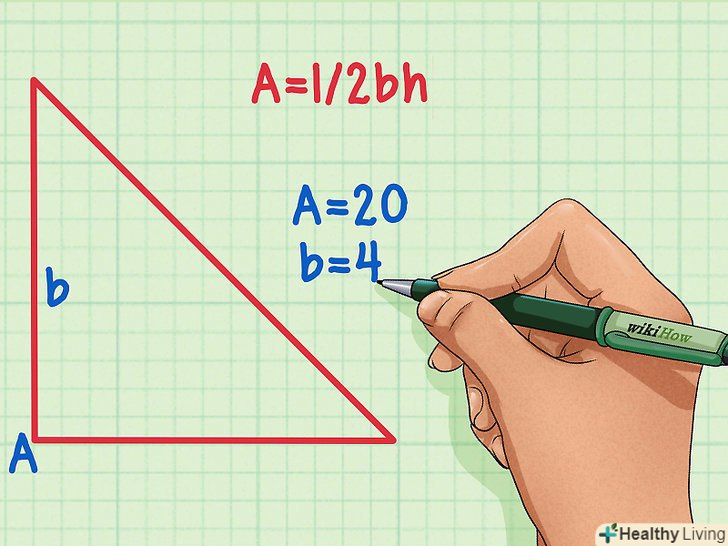
  2. Подивіться на трикутник і подумайте, які величини вам вже відомі.якщо вам дана площа, позначте її буквою»А " або "S". Вам також повинно бути дано значення сторони, позначте її буквою»b". Якщо вам не дана площа і не дана сторона, скористайтеся іншим методом.
    • Майте на увазі, що підставою трикутника може бути будь-яка його сторона, на яку опущена висота (незалежно від того, як розташований трикутник). Щоб краще зрозуміти це, уявіть, що ви можете повернути цей трикутник. Поверніть його так, щоб відома вам сторона була звернена вниз.
    • Наприклад, площа трикутника дорівнює 20, а одна з його сторін дорівнює 4. У цьому випадку " 'а = 20"', '"b = 4'".
  3. Підставте дані вам значення в формулу для обчислення площі (а = 1/2BH) і знайдіть висоту. спочатку помножте сторону (b) на 1/2, а потім розділіть площу (А) на отримане значення. Таким чином, ви знайдете висоту трикутника.
    • У нашому прикладі: 20 = 1/2(4)h
    • 20 = 2h
    • 10 = h

Метод2 З 3:
Як знайти висоту в рівносторонньому трикутнику

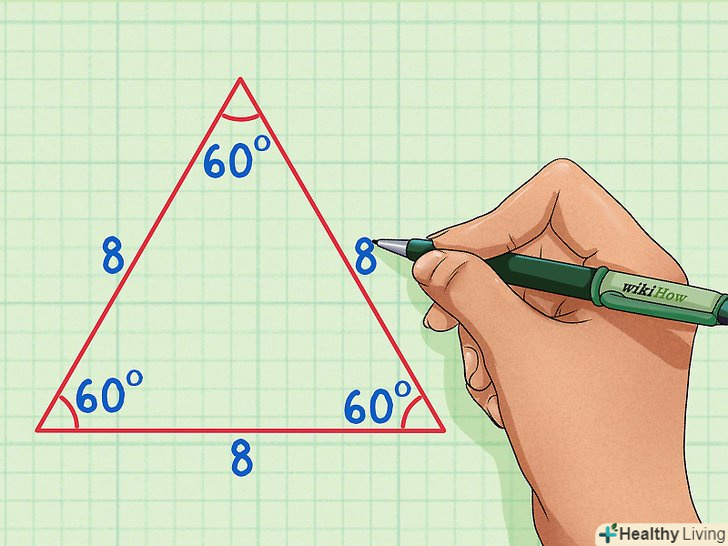
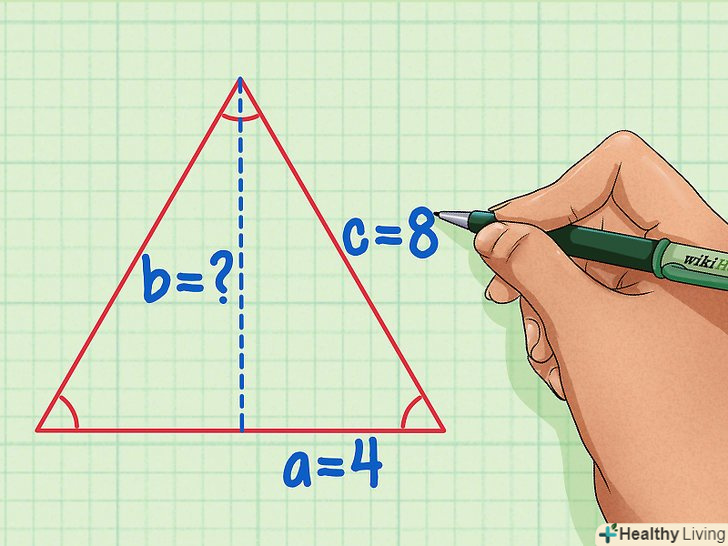
  1. Згадайте властивості рівностороннього трикутника. у рівносторонньому трикутнику всі сторони і всі кути рівні (кожен кут дорівнює 60). Якщо в такому трикутнику провести висоту, ви отримаєте два рівних прямокутних трикутника. [2]
    • Наприклад, розглянемо рівносторонній трикутник зі стороною 8.
  2. Згадайте теорему Піфагора. Теорема Піфагора говорить, що в будь-якому прямокутному трикутнику з катетами «А» і «b» гіпотенуза «с» дорівнює:A2+b2=c2 . Цю теорему можна використовувати, щоб знайти висоту рівностороннього трикутника![3]
  3. Розділіть рівносторонній трикутник на два прямокутних трикутника (для цього проведіть висоту).потім позначте сторони одного з прямокутних трикутників. Бічна сторона рівностороннього трикутника-це гіпотенуза» с " прямокутного трикутника. Катет "а «дорівнює 1/2 стороні рівностороннього трикутника, а катет» b" – це шукана висота рівностороннього трикутника.
    • Отже, в нашому прикладі з рівностороннім трикутником з відомою стороною, рівною 8:C = 8іA = 4.
  4. Підставте ці значення в теорему Піфагора і обчисліть b2 .спочатку зведіть в квадрат "с» і" А " (помножте кожне значення саме на себе). Потім відніміть a2 з c2.
    • 42 + b2 = 82
    • 16 + b2 = 64
    • B2 = 48
  5. Витягніть квадратний корінь з b2, щоб знайти висоту трикутника.для цього скористайтеся калькулятором. Отримане значення і буде висотою вашого рівностороннього трикутника!
    • B = √48 =6,93

Метод3 З 3:
Як знайти висоту з допомогою кутів і сторін

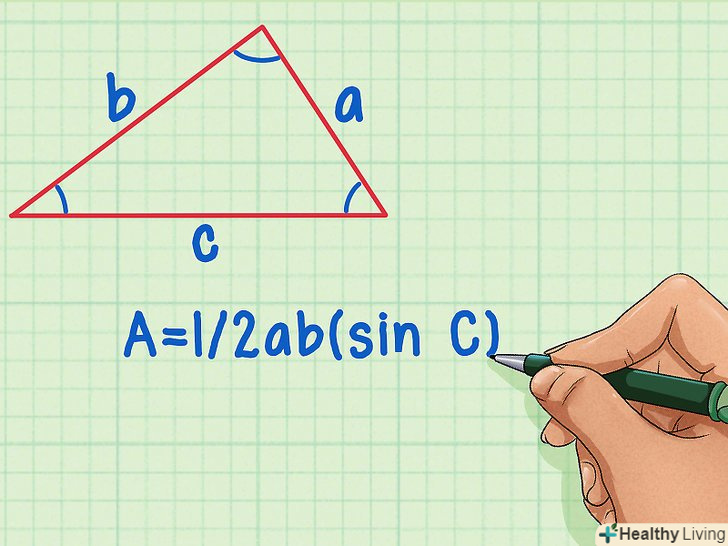
  1. Подумайте, які Значення вам відомі.ви можете знайти висоту трикутника, якщо вам відомі значення сторін і кутів. Наприклад, якщо відомий кут між підставою і бічною стороною. Або якщо відомі значення всіх трьох сторін. Отже, позначимо сторони трикутника:» a«,» b«,» c«, кути трикутника:» А«,» В«,» С«, а площа - буквою»S".
    • Якщо вам відомі всі три сторони, вам знадобиться значення площі трикутника і формула Герона.
    • Якщо вам відомі дві сторони і кут між ними, можете використовувати наступну формулу для знаходження площі: S=1/2AB(sinC).[4]
  2. Якщо вам дано значення всіх трьох сторін, використовуйте формулу Герона.за цією формулою доведеться виконати кілька дій. Спочатку потрібно знайти змінну " s " (ми позначимо цією буквою половину периметра трикутника). Для цього підставте відомі значення в цю формулу: s = (a+b+c)/2.[5]
    • Для трикутника зі сторонами а = 4, b = 3, c = 5, s = (4+3+5)/2. В результаті виходить: s=12/2, де s=6.
    • Потім другою дією ми знаходимо площу (друга частина формули Герона). Площа = √(s(s-a) (s-b) (s-c)). Замість слова «Площа» вставте еквівалентну формулу для пошуку площі: 1/2BH (або 1/2AH, або 1/2ch).
    • Тепер знайдіть еквівалентний вираз для висоти (h). Для нашого трикутника буде справедливим наступне рівняння: 1/2 (3) h = (6(6-4)(6-3)(6-5)). Де 3/2H=√(6(2(3(1))). Виходить, 3 / 2h = √(36). За допомогою калькулятора обчисліть квадратний корінь. У нашому прикладі: 3 / 2h = 6. Виходить, що висота (h) дорівнює 4, сторона b – підстава.
  3. Якщо за умовою завдання відомі дві сторони і кут, ви можете використовувати іншу формулу.Замініть площу у формулі еквівалентним виразом: 1/2bh. Таким чином, у вас вийде наступна формула: 1/2BH = 1/2AB(sinC). Її можна спростити до наступного виду: h = a (sin C), щоб прибрати одну невідому змінну.[6]
    • Тепер залишилося вирішити отримане рівняння. Наприклад, нехай "А « = 3,» С" = 40 градусів. Тоді рівняння буде виглядати так:» h " = 3(sin 40). За допомогою калькулятора і таблиці синусів підрахуйте значення "h". У нашому прикладі h = 1,928.

Джерела

  1. ↑ Http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html
  2. ↑ Http://www.mathsisfun.com/definitions/equilateral-triangle.html
  3. ↑ Http://www.mathsisfun.com/pythagoras.html
  4. ↑ Http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html
  5. ↑ Http://www.mathsisfun.com/geometry/herons-formula.html
  6. ↑ Http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html

Ще почитати: