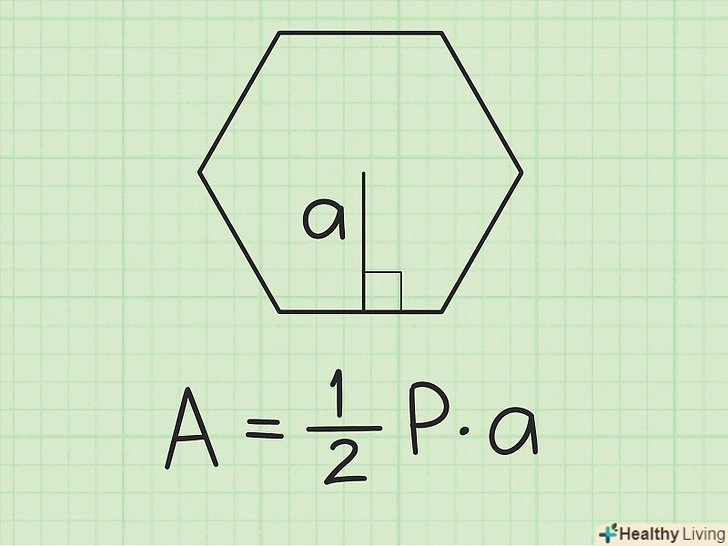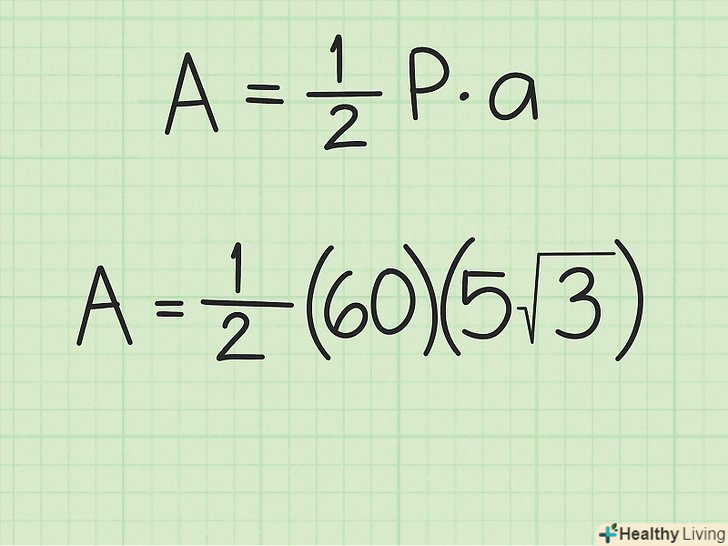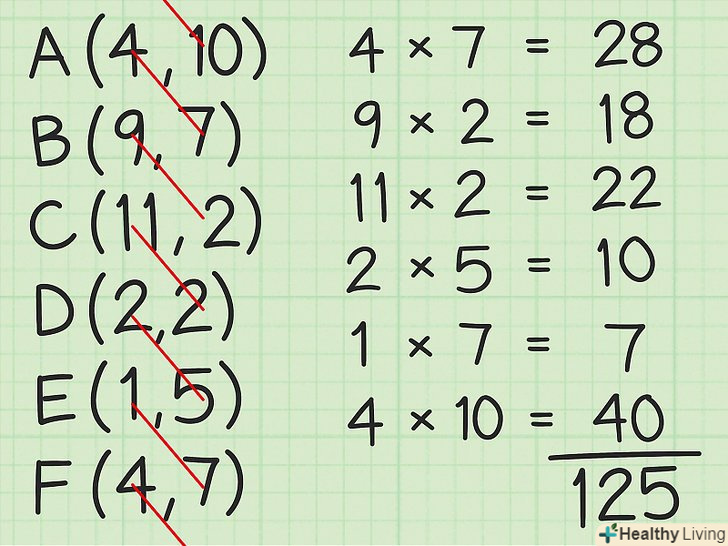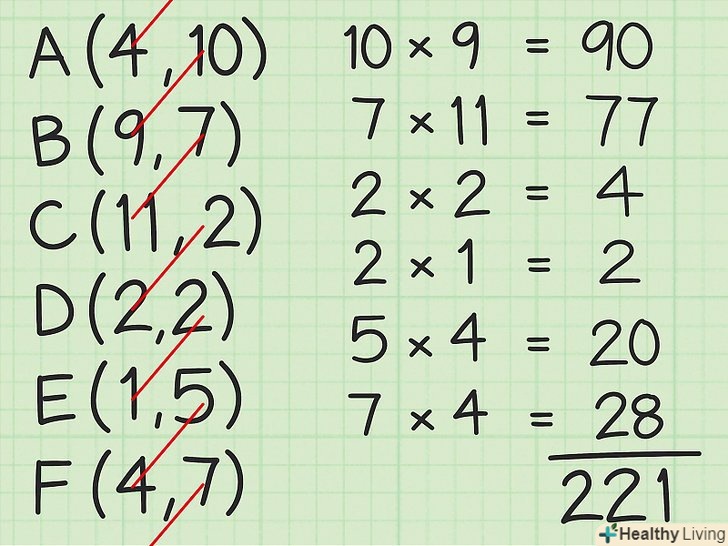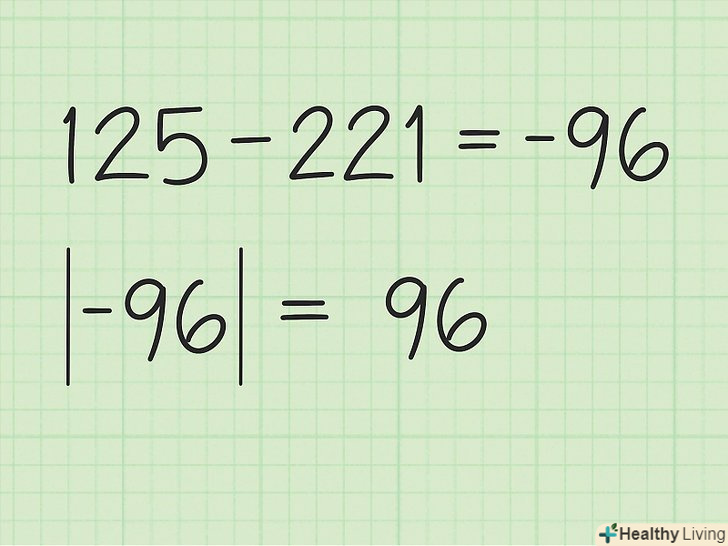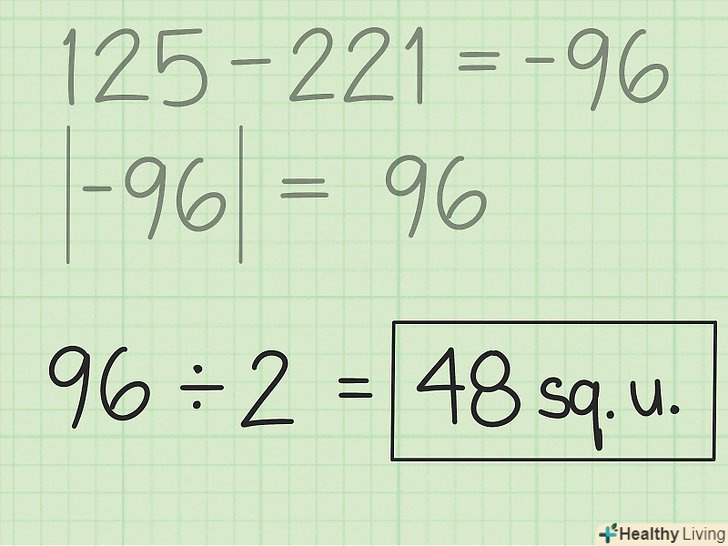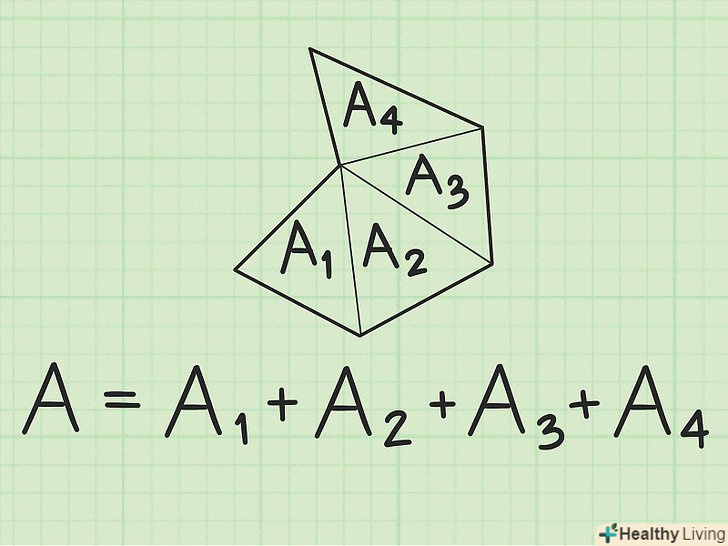Шестикутник-це багатокутник, що має шість сторін і шість кутів. У правильному шестикутнику всі сторони рівні, а кути утворюють шість рівносторонніх трикутників. Є кілька способів знайти площу шестикутника, залежно від того, чи маєте Ви справу з правильним або неправильним шестикутником. З цієї статті ви дізнаєтеся, як саме знаходити площу цієї фігури.
Кроки
Метод1З 4:
Як знайти площа шестикутника при відомій довжині сторони
Метод1З 4:
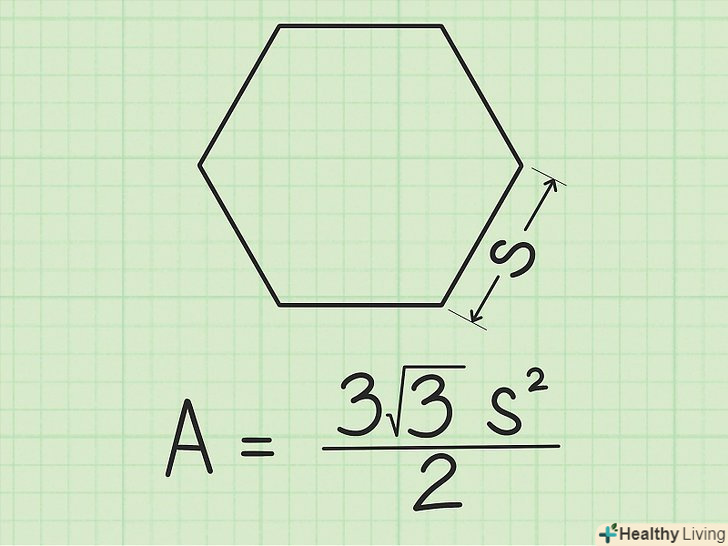
 Запишіть формулу. Так як правильний шестикутник складається з 6 рівносторонніх трикутників, то формула утворена з формули знаходження площі рівностороннього трикутника: Площа = (3√3 s2)/ 2 де S — довжина сторони правильного шестикутника.[1]
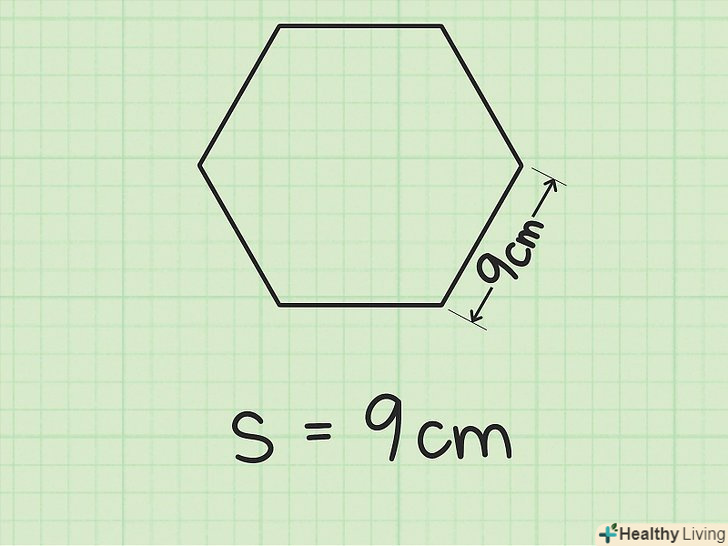
Запишіть формулу. Так як правильний шестикутник складається з 6 рівносторонніх трикутників, то формула утворена з формули знаходження площі рівностороннього трикутника: Площа = (3√3 s2)/ 2 де S — довжина сторони правильного шестикутника.[1] Визначте довжину однієї сторони.якщо відома довжина сторони, то просто запишіть її. У нашому випадку довжина сторони-9 см. якщо довжина сторони невідома, але відомий периметр або апофема (висота одного з шести рівносторонніх трикутників, перпендикулярна стороні), то можна знайти і довжину сторони. Ось, як це робиться:
Визначте довжину однієї сторони.якщо відома довжина сторони, то просто запишіть її. У нашому випадку довжина сторони-9 см. якщо довжина сторони невідома, але відомий периметр або апофема (висота одного з шести рівносторонніх трикутників, перпендикулярна стороні), то можна знайти і довжину сторони. Ось, як це робиться:- Якщо відомий периметр, то просто розділіть його на 6 і отримаєте довжину сторони. Якщо, наприклад, периметр - 54 см, то, розділивши 54 на 6, ми отримаємо 9 см, довжину сторони.[2]
- Якщо відома тільки апофема, то довжину сторони можна обчислити, підставивши апофему в формулуa = x√3 і потім помноживши відповідь на 2. Це робиться тому, що апофема являє собою сторону x√3 утвореного їй трикутника з кутами 30-60-90 градусів. Якщо, наприклад, апофема — 10√3, то x — 10 і довжина сторони буде дорівнює 10 * 2 або 20.
 Підставте значення довжини сторони в формулу.просто підставляємо 9 в початкову формулу. Отримуємо: площа = (3√3 x 92)/2
Підставте значення довжини сторони в формулу.просто підставляємо 9 в початкову формулу. Отримуємо: площа = (3√3 x 92)/2 Спростіть відповідь.Вирішіть рівняння і запишіть відповідь. Відповідь повинна бути вказана в квадратних одиницях, адже ми маємо справу з площею. Ось, як це робиться:
Спростіть відповідь.Вирішіть рівняння і запишіть відповідь. Відповідь повинна бути вказана в квадратних одиницях, адже ми маємо справу з площею. Ось, як це робиться:- (3√3 x 92)/2 =
- (3√3 x 81)/2 =
- (243√3)/2 =
- 420.8/2 =
- 210.4 см2
Метод2З 4:
Як знайти площу правильного шестикутника, якщо відома апофема
Метод2З 4:
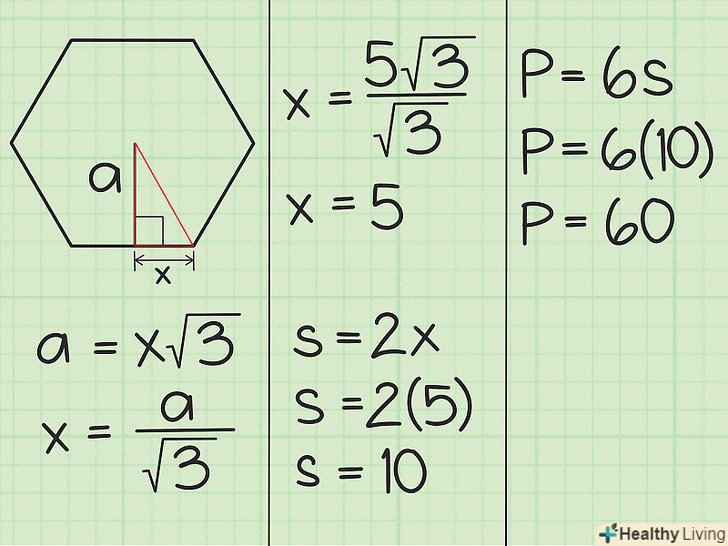
 Запишіть формулу.Площа = 1/2 x периметр x апофему.[3]
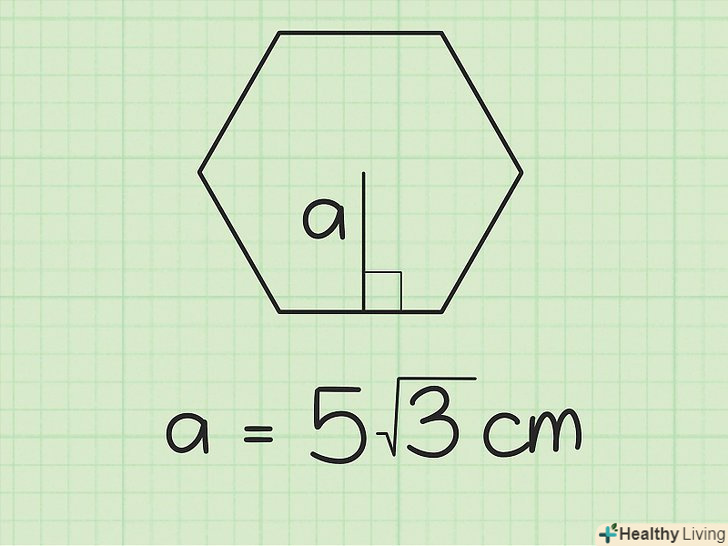
Запишіть формулу.Площа = 1/2 x периметр x апофему.[3] Запишіть апофему.скажімо, вона дорівнює 5√3 см.
Запишіть апофему.скажімо, вона дорівнює 5√3 см. Використовуйте апофему для знаходження периметра.Апофема перпендикулярна стороні шестикутника і створює трикутник з кутами 30-60-90. Сторони такого трикутника відповідають пропорції x-x√3-2x, де сторона короткої сторони, що лежить навпроти кута в 30 градусів, представлена x, довжина довгої сторони, що лежить навпроти кута в 60 градусів, представлена x√3, а гіпотенуза представлена 2x.[4]
Використовуйте апофему для знаходження периметра.Апофема перпендикулярна стороні шестикутника і створює трикутник з кутами 30-60-90. Сторони такого трикутника відповідають пропорції x-x√3-2x, де сторона короткої сторони, що лежить навпроти кута в 30 градусів, представлена x, довжина довгої сторони, що лежить навпроти кута в 60 градусів, представлена x√3, а гіпотенуза представлена 2x.[4]- Апофема-сторона, представлена x√3. Таким чином, підставляємо апофему в формулуa = x√3 і вирішуємо. Якщо, наприклад, довжина апофеми-5√3, то підставляємо це число в формулу і отримуємо 5√3 см = x√3, або x = 5 см.
- Вирішуючи через x, ми знайшли довжину короткої сторони трикутника-5 см. ця довжина являє собою половину довжини сторони шестикутника. Помноживши 5 на 2, ми отримуємо 10 см, довжину сторони.
- Підрахувавши, що довжина сторони дорівнює 10, множимо це число на 6 і отримуємо периметр шестикутника. 10 см х 6 = 60 см.
 Підставте всі відомі дані в формулу.найскладніше знайти периметр. Тепер треба лише підставити апофему і периметр в формулу і вирішити:
Підставте всі відомі дані в формулу.найскладніше знайти периметр. Тепер треба лише підставити апофему і периметр в формулу і вирішити:- Площа = 1/2 x периметр x апофему
- Площа = 1/2 x 60 см x 5√3 см
 Спрощуйте відповідь до тих пір, поки не позбудетеся від квадратних коренів.остаточну відповідь вкажіть у квадратних одиницях.
Спрощуйте відповідь до тих пір, поки не позбудетеся від квадратних коренів.остаточну відповідь вкажіть у квадратних одиницях.- 1/2 x 60 см x 5√3 см =
- 30 x 5√3 см =
- 150√3 см =
- 259. 8 см2
Метод3З 4:
Як знайти площу багатогранника при відомих координатах вершин
Метод3З 4:
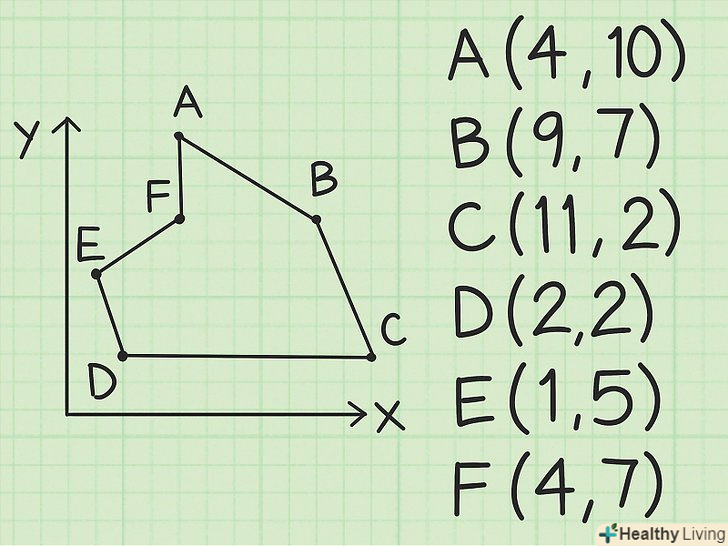
 Запишіть координати всіх вершин по осях x і y. якщо відомі вершини шестикутника, то насамперед треба накреслити таблицю з двома колонками і сім'ю рядами. Кожен ряд буде названий за назвою по одній з шести точок (точка А, точка В, точка С і так далі), кожна колонка буде названа по осях x або у, відповідним координатам точок по цих осях. Запишіть координати точки А по осях x і у праворуч від точки, координати точки в — праворуч від точки В і так далі. Внизу повторно вкажіть координати першої точки. Для прикладу скажемо, що ми маємо справу з наступними точками, у форматі (x, у):[5]
Запишіть координати всіх вершин по осях x і y. якщо відомі вершини шестикутника, то насамперед треба накреслити таблицю з двома колонками і сім'ю рядами. Кожен ряд буде названий за назвою по одній з шести точок (точка А, точка В, точка С і так далі), кожна колонка буде названа по осях x або у, відповідним координатам точок по цих осях. Запишіть координати точки А по осях x і у праворуч від точки, координати точки в — праворуч від точки В і так далі. Внизу повторно вкажіть координати першої точки. Для прикладу скажемо, що ми маємо справу з наступними точками, у форматі (x, у):[5]- A: (4, 10)
- B: (9, 7)
- C: (11, 2)
- D: (2, 2)
- E: (1, 5)
- F: (4, 7)
- A (знову): (4, 10)
 Помножте координати кожної точки по осі x на координати по осі у наступної точки.це можна уявити собі так: ми проводимо діагональ вниз і вправо від кожної координати по осі x. запишемо результати праворуч від таблиці. Потім складемо їх.
Помножте координати кожної точки по осі x на координати по осі у наступної точки.це можна уявити собі так: ми проводимо діагональ вниз і вправо від кожної координати по осі x. запишемо результати праворуч від таблиці. Потім складемо їх.- 4 x 7 = 28
- 9 x 2 = 18
- 11 x 2 = 22
- 2 x 5 = 10
- 1 x 7 = 7
- 4 x 10 = 40
- 28 + 18 + 22 + 10 + 7 + 40 = 125
 Помножте координати кожної точки по осі у на координати по осі x наступної точки.це можна уявити собі так: ми проводимо діагональ вниз і вліво від кожної координати по осі У. перемноживши всі координати, складаємо результати.
Помножте координати кожної точки по осі у на координати по осі x наступної точки.це можна уявити собі так: ми проводимо діагональ вниз і вліво від кожної координати по осі У. перемноживши всі координати, складаємо результати.- 10 x 9 = 90
- 7 x 11 = 77
- 2 x 2 = 4
- 2 x 1 = 2
- 5 x 4 = 20
- 7 x 4 = 28
- 90 + 77 + 4 + 2 + 20 + 28 = 221
 Відніміть з першої суми координат другу суму координат.віднімаємо 221 з 125 і отримуємо -96. Отже, відповідь: 96, площа може бути тільки позитивною.
Відніміть з першої суми координат другу суму координат.віднімаємо 221 з 125 і отримуємо -96. Отже, відповідь: 96, площа може бути тільки позитивною. Розділіть різницю на два.ділимо 96 на 2 і отримуємо площу неправильного шестикутника. Остаточна відповідь: 48 квадратних одиниць.
Розділіть різницю на два.ділимо 96 на 2 і отримуємо площу неправильного шестикутника. Остаточна відповідь: 48 квадратних одиниць.
Метод4З 4:
Інші способи знаходження площі неправильного шестикутника
Метод4З 4:
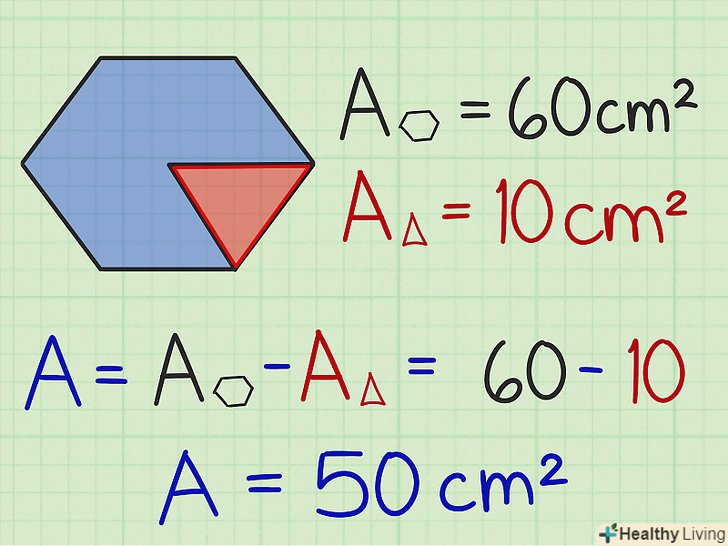
 Знайдіть площу правильного шестикутника з відсутнім трикутником.якщо ви зіткнулися з правильним шестикутником, в якому відсутній один або більше трикутників, то перш за все потрібно знайти його площа, як якщо б він був цілим. Потім необхідно знайти площу "відсутнього" трикутника і відняти її із загальної площі. У підсумку ви отримаєте площу наявної фігури.[6]
Знайдіть площу правильного шестикутника з відсутнім трикутником.якщо ви зіткнулися з правильним шестикутником, в якому відсутній один або більше трикутників, то перш за все потрібно знайти його площа, як якщо б він був цілим. Потім необхідно знайти площу "відсутнього" трикутника і відняти її із загальної площі. У підсумку ви отримаєте площу наявної фігури.[6]- Наприклад, якщо ми з'ясували, що площа правильного трикутника-60 см2, а площа відсутнього трикутника — 10 см2, то: 60 см2 - 10 см2 = 50 см2.
- Якщо відомо, що в шестикутнику не вистачає точно одного трикутника, то його площа можна знайти, помноживши загальну площу на 5/6, так як ми маємо 5 і 6 трикутників. Якщо не вистачає двох трикутників, то множимо на 4/6 (2/3) і так далі.
 Розбийте неправильний шестикутник на трикутники. знайдіть площі трикутників і складіть їх. Залежно від наявних даних існує безліч способів знайти площу трикутника.[7]
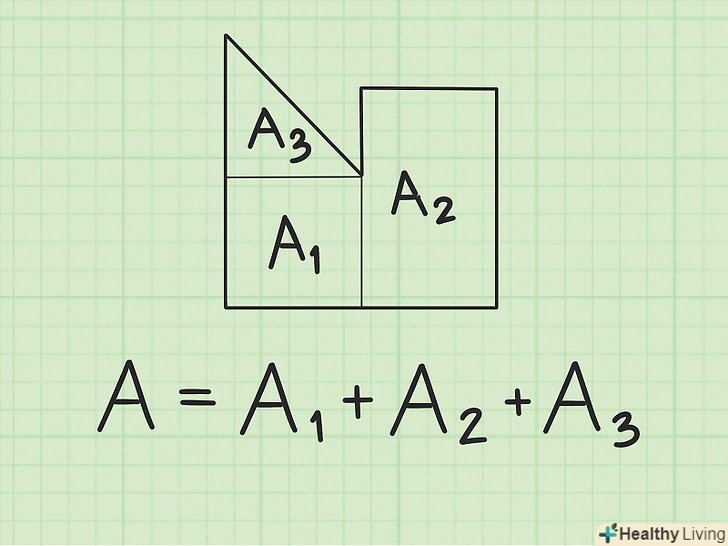
Розбийте неправильний шестикутник на трикутники. знайдіть площі трикутників і складіть їх. Залежно від наявних даних існує безліч способів знайти площу трикутника.[7] Знайдіть в неправильному шестикутнику якісь інші фігури: трикутники, прямокутники, квадрати. Знайдіть площі складових шестикутник фігур і складіть їх.[8]
Знайдіть в неправильному шестикутнику якісь інші фігури: трикутники, прямокутники, квадрати. Знайдіть площі складових шестикутник фігур і складіть їх.[8]- Один з видів неправильного шестикутника складається з двох паралелограмів. Для знаходження їх площ просто перемножте підстави на висоти і потім складіть їх площі.
Джерела
- ↑ Http://www.drking.org.uk/hexagons/misc/area.html
- ↑ Https://sciencing.com/calculate-length-sides-regular-hexagons-6001248.html
- ↑ Http://www.dummies.com/how-to/content/how-to-calculate-the-area-of-a-regular-hexagon.html
- ↑ Http://jwilson.coe.uga.edu/emat6680/parsons/mvp6690/unit/hexagon/hexagon.html
- ↑ Http://www.mathopenref.com/coordpolygonarea.html
- ↑ Https://www.mathopenref.com/polygonirregulararea.html
- ↑ Https://www.mathopenref.com/polygonirregulararea.html
- ↑ Https://www.mathopenref.com/polygonirregulararea.html