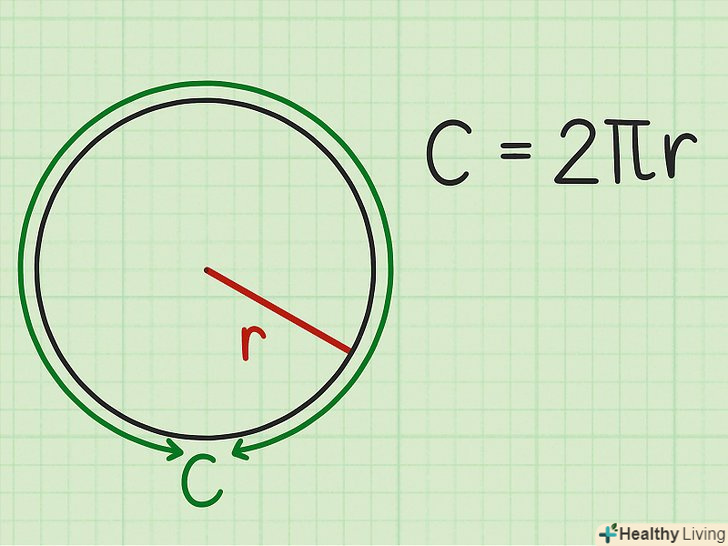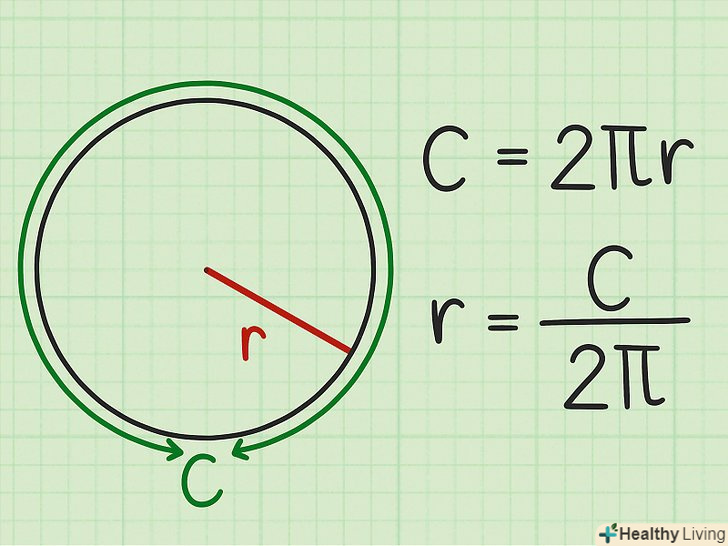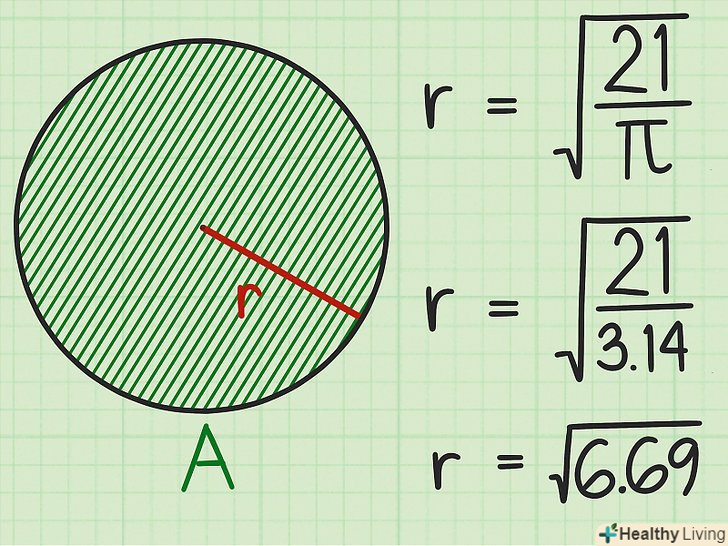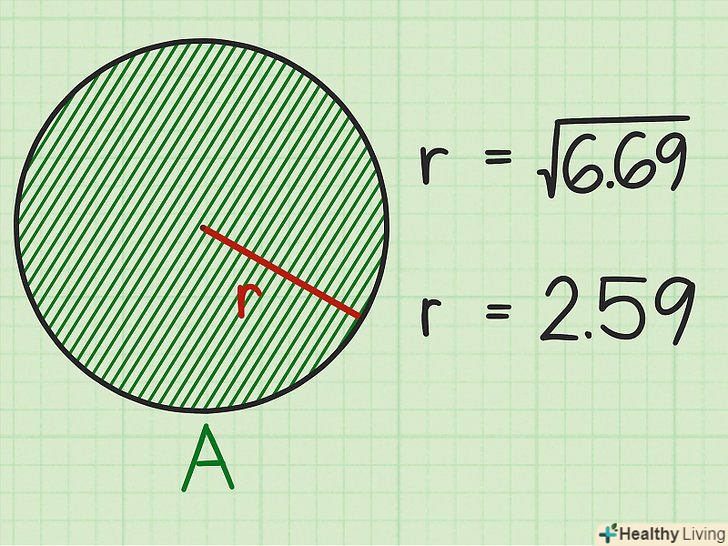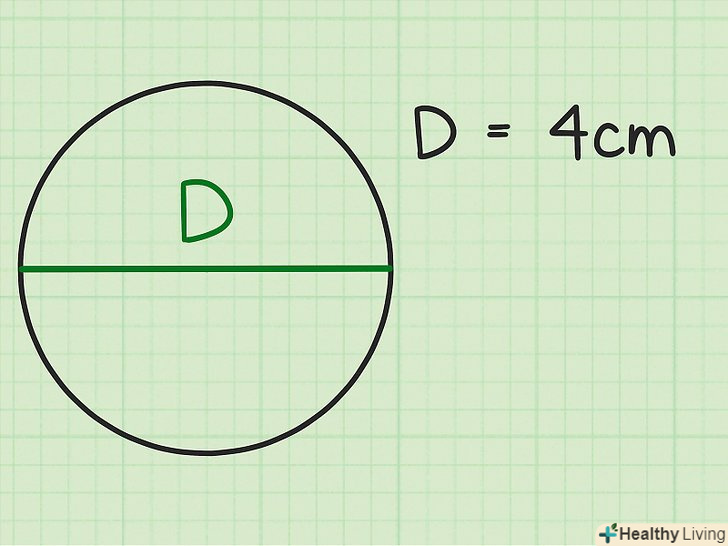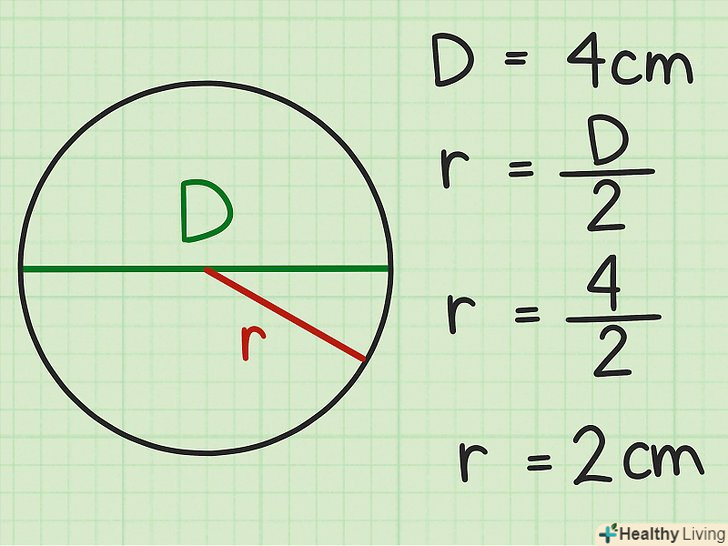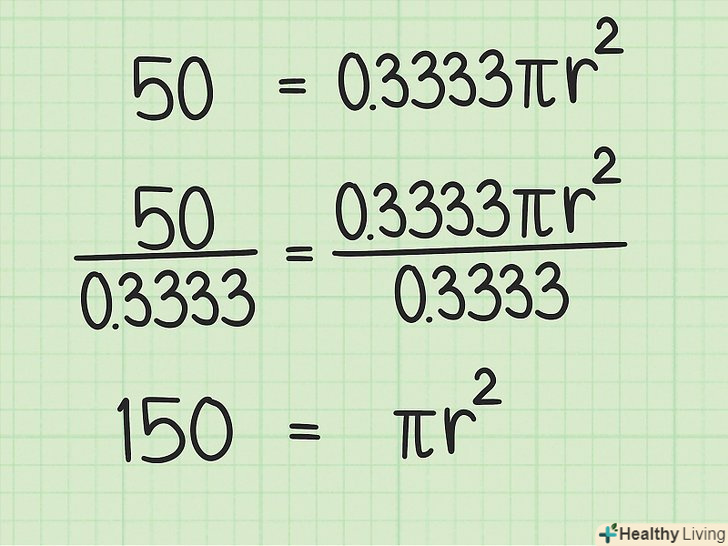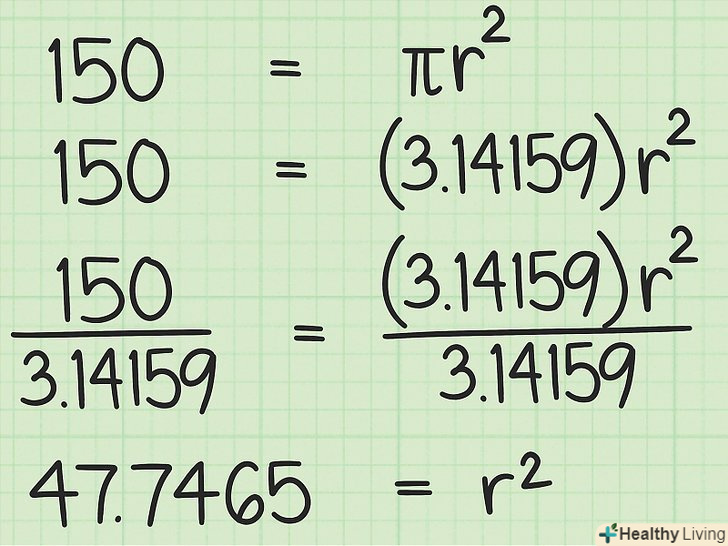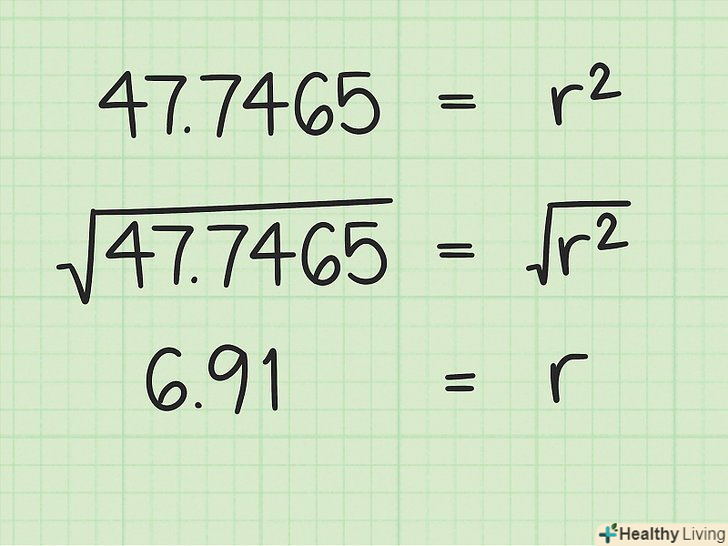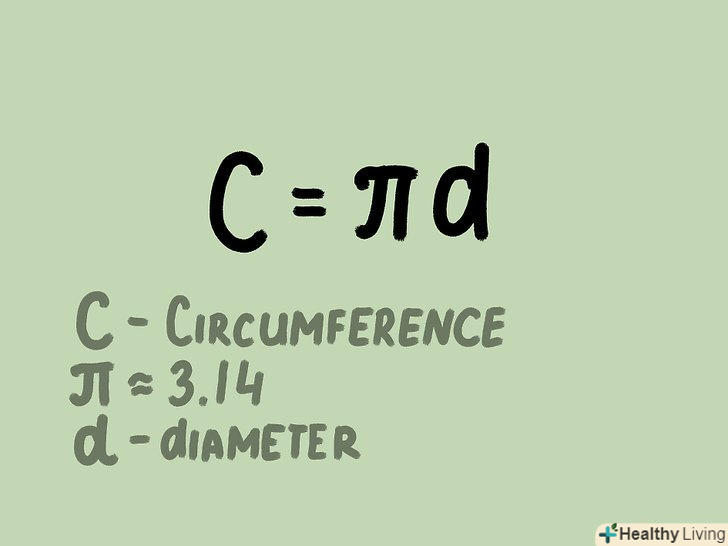Радіус кола-це відстань від центру кола до будь-якої точки, яка лежить на зовнішній окружності кола.[1] найпростіший спосіб знайти радіус-розділити діаметр навпіл. Якщо діаметр не відомий, але дані значення інших величин, таких як довжина кола () або площа кола (
), радіус можна обчислити за спеціальними формулами, ізолювавши змінну
. Нарешті, якщо дано центральний кут і площа сектора кола, можна скористатися формулою
, щоб знайти радіус. Зверніть увагу, що в даній статті площа позначена як
, але в російських підручниках прийнято позначення
.
Кроки
Метод1З 4:
По довжині кола
Метод1З 4:
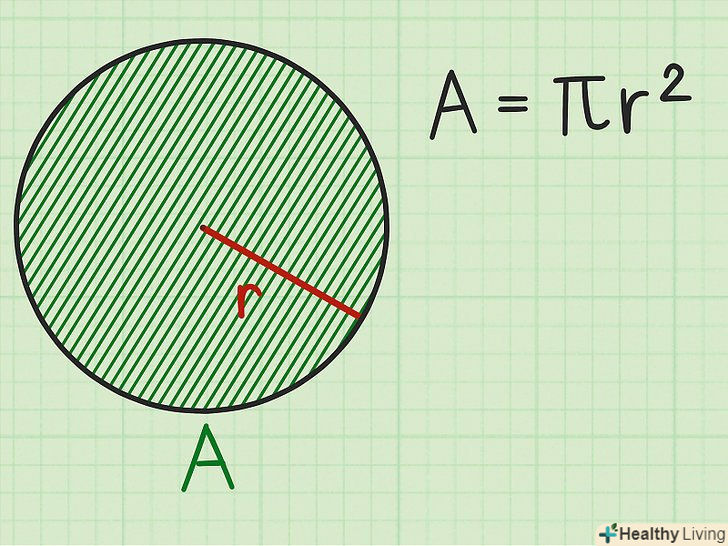
 Запишіть формулу для обчислення довжини кола. Формула:
Запишіть формулу для обчислення довжини кола. Формула:, де
– довжина окружності,
– радіус кола (кола).[2]
- Число
приблизно дорівнює 3,14. Можете також використовувати відповідний символ на калькуляторі.
- Число
 У формулі ізолюйте радіус. для цього розділіть обидві частини формули на
У формулі ізолюйте радіус. для цього розділіть обидві частини формули на. Ви отримаєте формулу для обчислення радіуса.
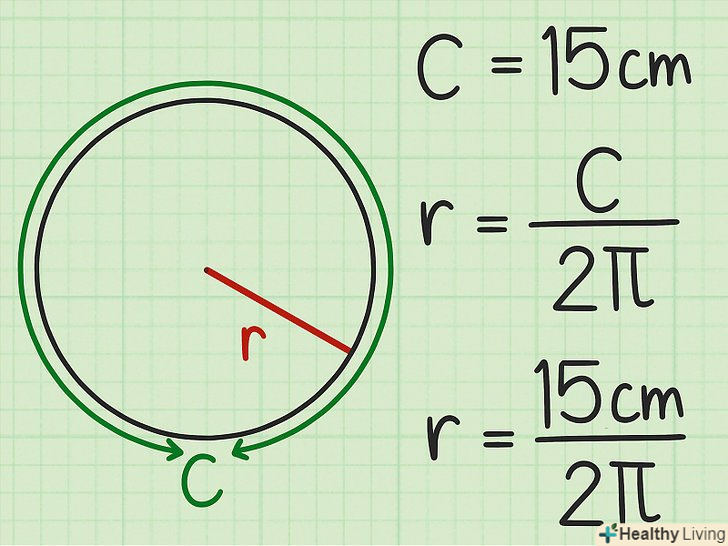
 У формулу підставте значення довжини кола. воно повинно бути дано в завданні. Значення довжини кола підставляється замість змінної
У формулу підставте значення довжини кола. воно повинно бути дано в завданні. Значення довжини кола підставляється замість змінної.
- Наприклад, якщо довжина кола дорівнює 15 см, формула запишеться так:
.
- Наприклад, якщо довжина кола дорівнює 15 см, формула запишеться так:
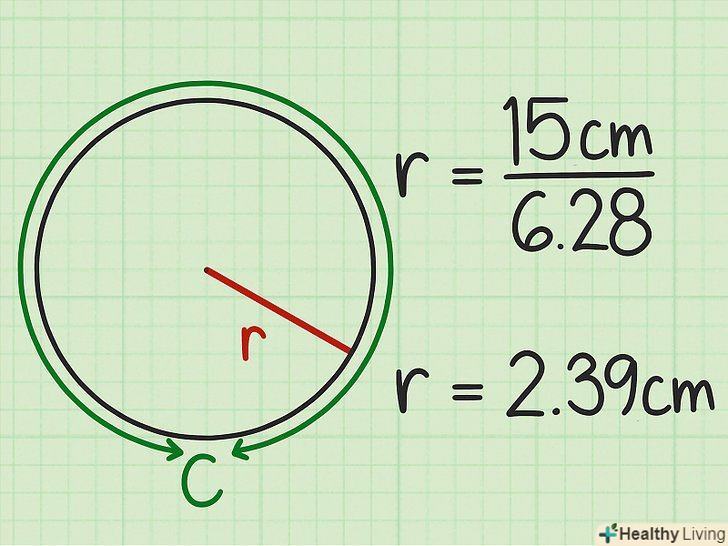
 Округліть результат. розрахуйте величину радіуса, використовуючи клавішу
Округліть результат. розрахуйте величину радіуса, використовуючи клавішуна калькуляторі і округліть відповідь. Якщо у вас немає калькулятора або на ньому немає такої клавіші, розрахуйте вручну, прийнявши
рівним 3,14.
- Наприклад,
приблизно
приблизно 2,39 см.
- Наприклад,
Метод2З 4:
По площі кола
Метод2З 4:

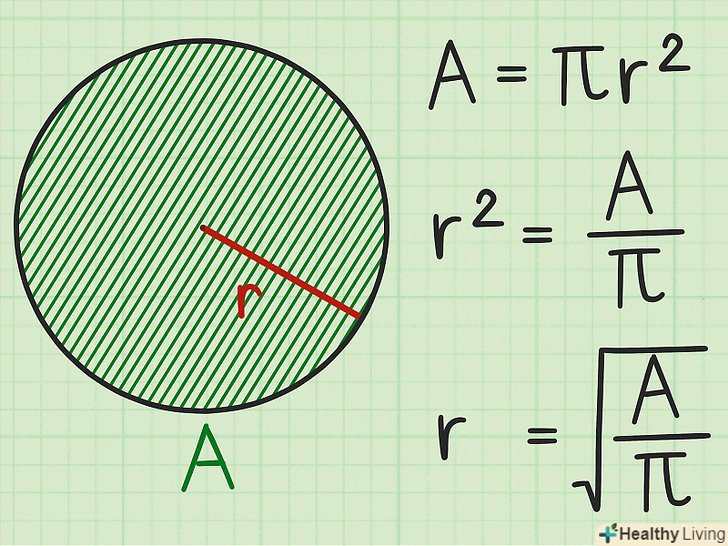
 У формулі ізолюйте радіус.
У формулі ізолюйте радіус.- Спочатку розділіть обидві частини формули на
:
- Потім з обох частин формули витягніть квадратний корінь.
- Спочатку розділіть обидві частини формули на
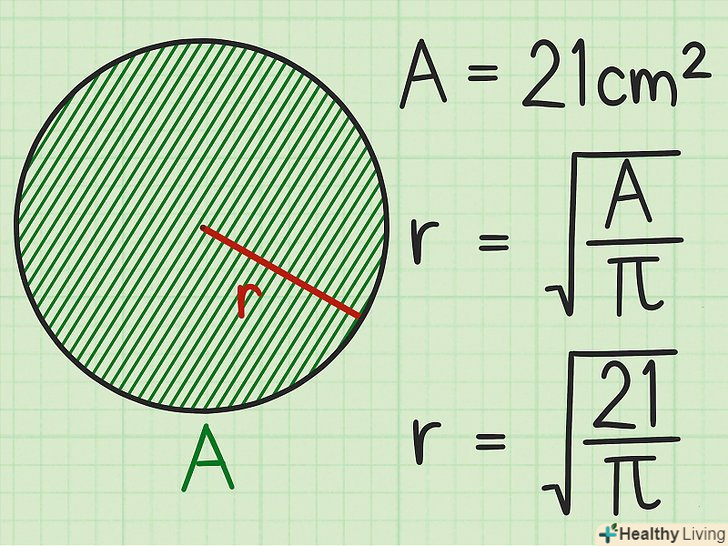
 У формулу підставте значення площі. воно повинно бути дано в завданні. Значення площі підставляється замість змінної
У формулу підставте значення площі. воно повинно бути дано в завданні. Значення площі підставляється замість змінної.
- Наприклад, якщо площа кола дорівнює 21 см2, то формула запишеться так:
.
- Наприклад, якщо площа кола дорівнює 21 см2, то формула запишеться так:
 Розділіть площу на
Розділіть площу на.щоб отримати точне значення, скористайтеся калькулятором. Якщо немає калькулятора, округліть
до 3,14.
- Якщо ви, Наприклад, число округлили
до 3,14, то:
- Якщо на вашому калькуляторі можна ввести відразу всю формулу, відповідь вийде більш точним.
- Якщо ви, Наприклад, число округлили
 Витягніть квадратний корінь.для цього знадобиться калькулятор, тому що в результаті вийде десятковий дріб. Так ви обчислите радіус кола.
Витягніть квадратний корінь.для цього знадобиться калькулятор, тому що в результаті вийде десятковий дріб. Так ви обчислите радіус кола.- Наприклад,
. Таким чином, радіус кола, площа якого дорівнює 21 см2, приблизно дорівнює 2,59 см.
- Наприклад,
Метод3З 4:
По діаметру
Метод3З 4:
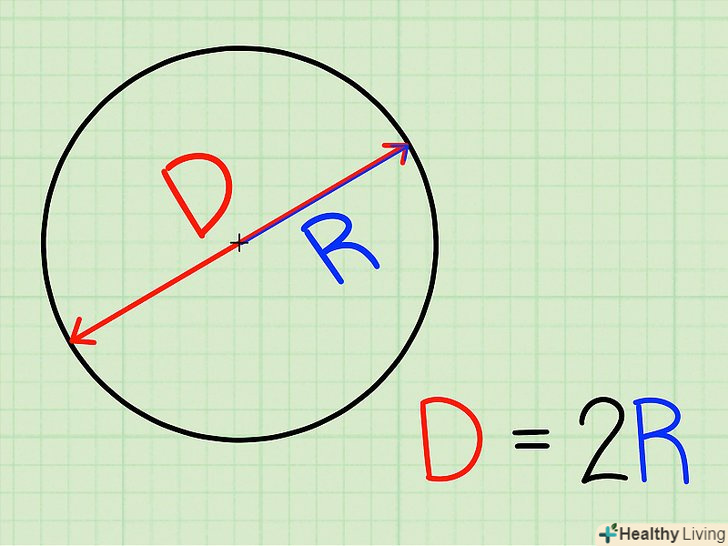
 Знайдіть діаметр кола.як правило, діаметр дано в завданні; в іншому випадку просто виміряйте його. Діаметр-це відрізок, який з'єднує дві точки, що лежать на окружності, і проходить через центр кола (кола).[4] Діаметр ділить коло на дві рівні частини.
Знайдіть діаметр кола.як правило, діаметр дано в завданні; в іншому випадку просто виміряйте його. Діаметр-це відрізок, який з'єднує дві точки, що лежать на окружності, і проходить через центр кола (кола).[4] Діаметр ділить коло на дві рівні частини.- Наприклад, дано коло діаметром 4 см.
 Розділіть діаметр на 2.радіус кола дорівнює половині його діаметра.[5]
Розділіть діаметр на 2.радіус кола дорівнює половині його діаметра.[5]- Наприклад, якщо діаметр дорівнює 4 см, то:
. Таким чином, радіус кола дорівнює 2 см.
- Наприклад, якщо діаметр дорівнює 4 см, то:
Метод4З 4:
За площею сектора і центральному кутку
Метод4З 4:
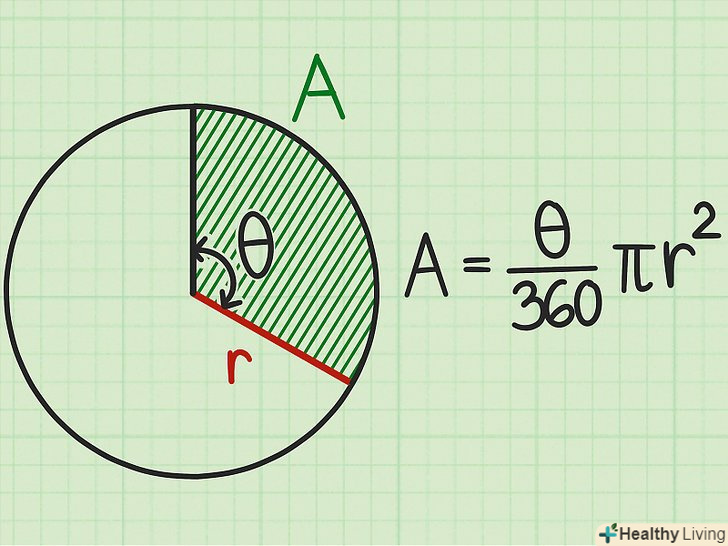
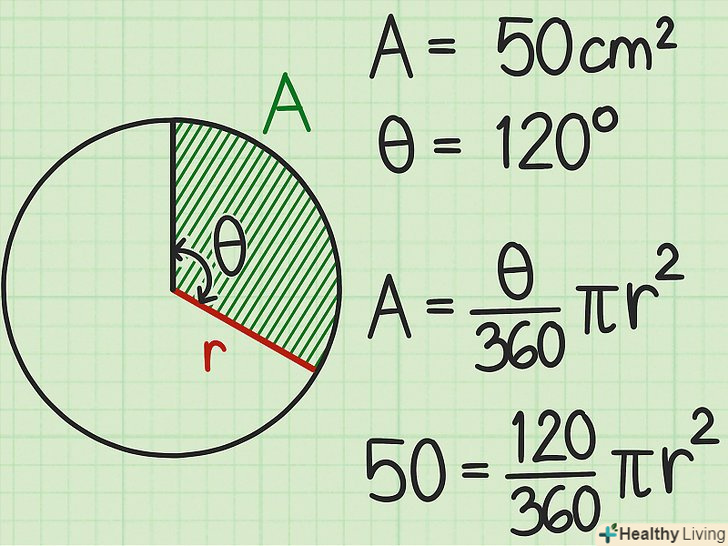
 Запишіть формулу для обчислення площі сектора. Формула:
Запишіть формулу для обчислення площі сектора. Формула:, де
– площа сектора,
– центральний кут,
– радіус кола.[6]
 У формулу підставте значення площі сектора і центрального кута. ці значення повинні бути дані в завданні. Переконайтеся, що відома площа сектора, а не площа кола. Значення площі сектора підставляється замість змінної
У формулу підставте значення площі сектора і центрального кута. ці значення повинні бути дані в завданні. Переконайтеся, що відома площа сектора, а не площа кола. Значення площі сектора підставляється замість змінної, а значення центрального кута замість змінної
.
- Наприклад, якщо площа сектора дорівнює 50 см2, а центральний кут дорівнює 120 градусів, формула запишеться наступним чином:
.
- Наприклад, якщо площа сектора дорівнює 50 см2, а центральний кут дорівнює 120 градусів, формула запишеться наступним чином:
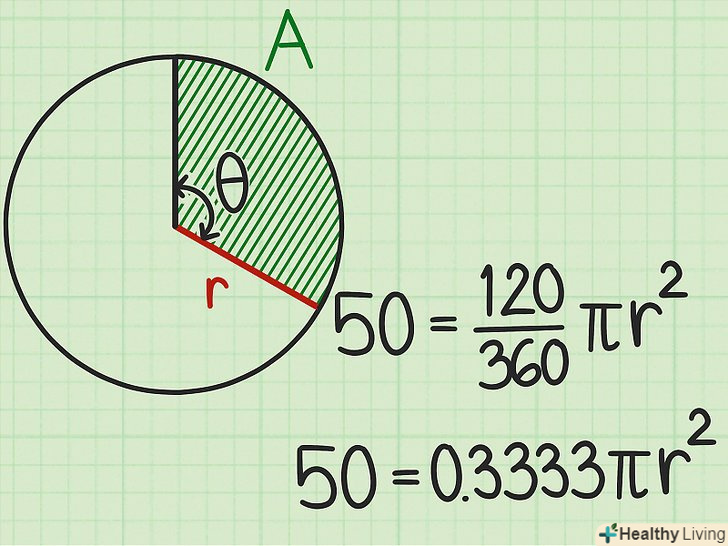
 Розділіть центральний кут на 360.так ви визначите, яку частину кола займає сектор.
Розділіть центральний кут на 360.так ви визначите, яку частину кола займає сектор.- Наприклад,
=
. Таким чином, сектор займає
частина кола. Формула запишеться так:
- Наприклад,
 Ізолюйте
Ізолюйте.для цього розділіть обидві частини формули на звичайний дріб або десятковий дріб, рівну частині, яку займає сектор на колі. Якщо ви не користуєтеся калькулятором, ділите на звичайний дріб. За допомогою калькулятора можна розділити на десятковий дріб, але пам'ятайте, що чим менше цифр після десяткової коми, тим менш точний результат ви отримаєте.
- Наприклад:
- Наприклад:
 Розділіть обидві частини формули на
Розділіть обидві частини формули на. так ви ізолюєте змінну
. Щоб отримати більш точний результат, скористайтеся калькулятором. Число
округліть до 3,14159 або до 3,14.
- Наприклад:
- Наприклад:
 Витягніть квадратний корінь з обох частин формули.так ви знайдете радіус кола.
Витягніть квадратний корінь з обох частин формули.так ви знайдете радіус кола.- Наприклад:
Таким чином, радіус кола дорівнює приблизно 6,91 див.
- Наприклад: