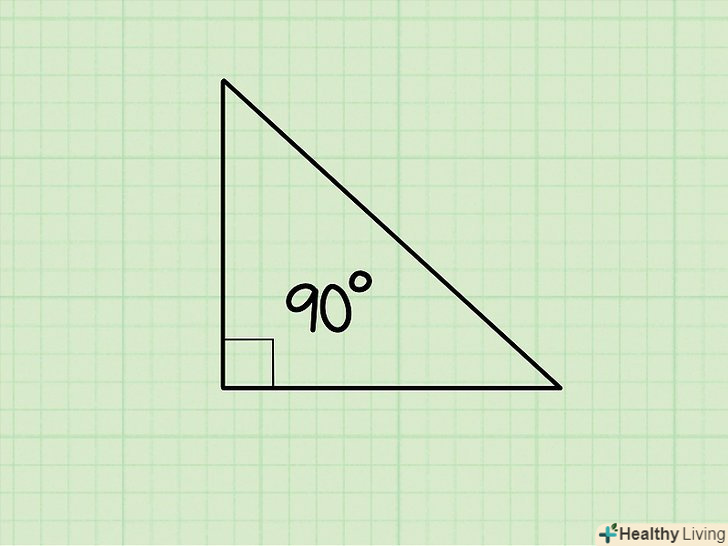
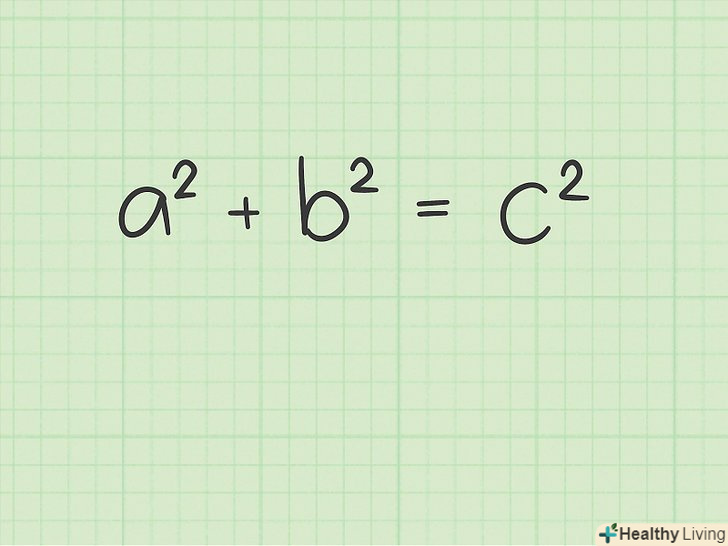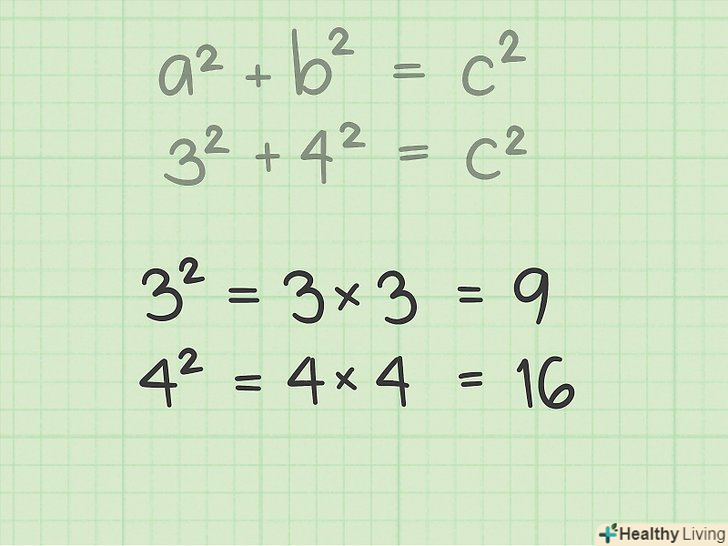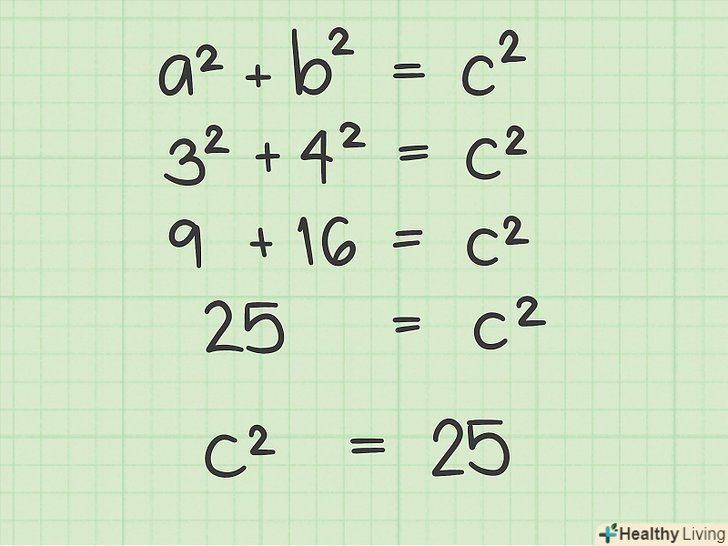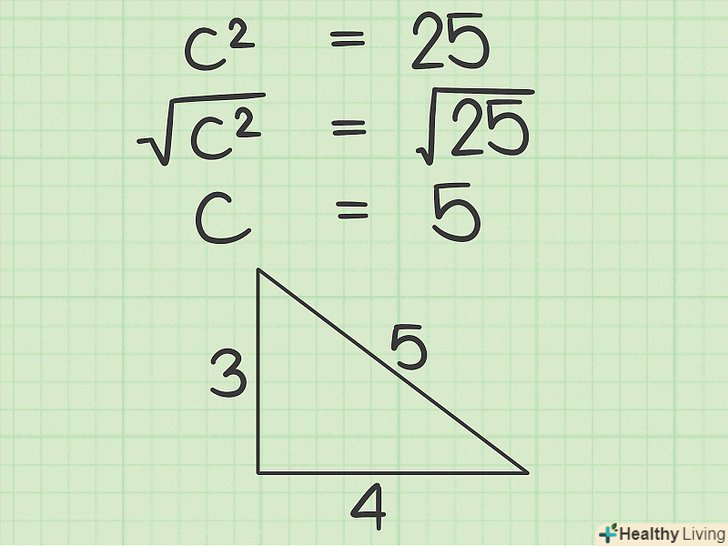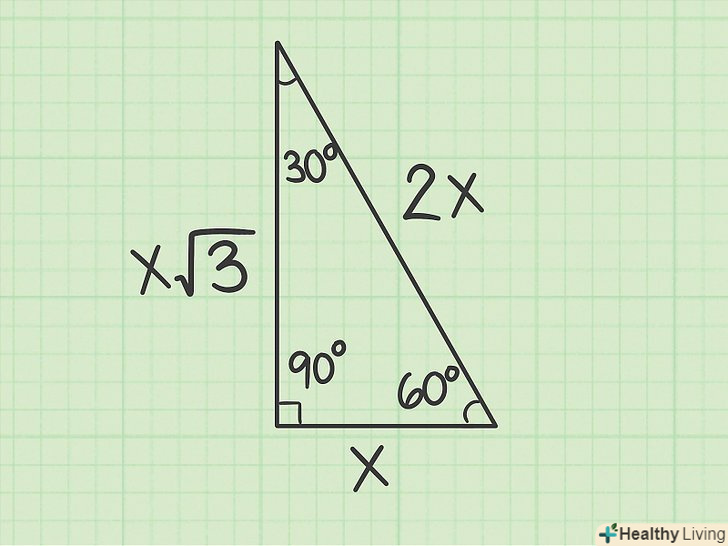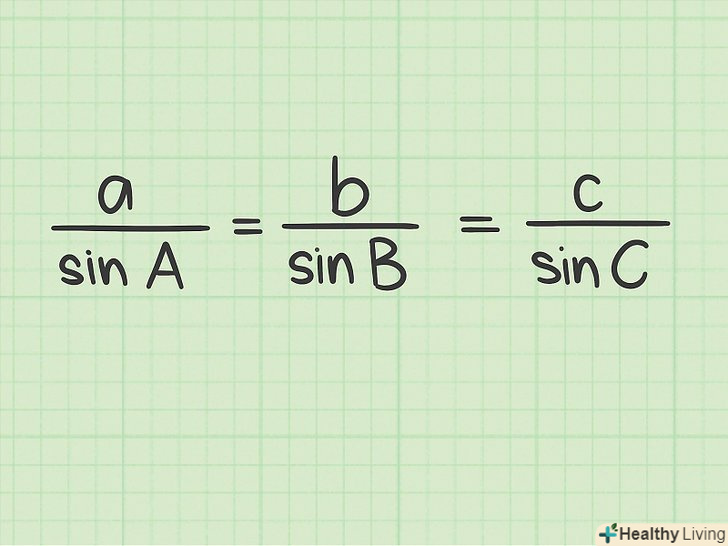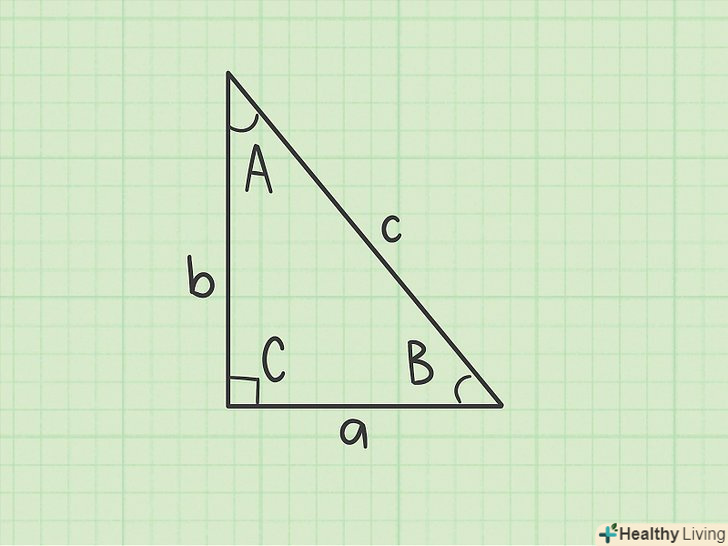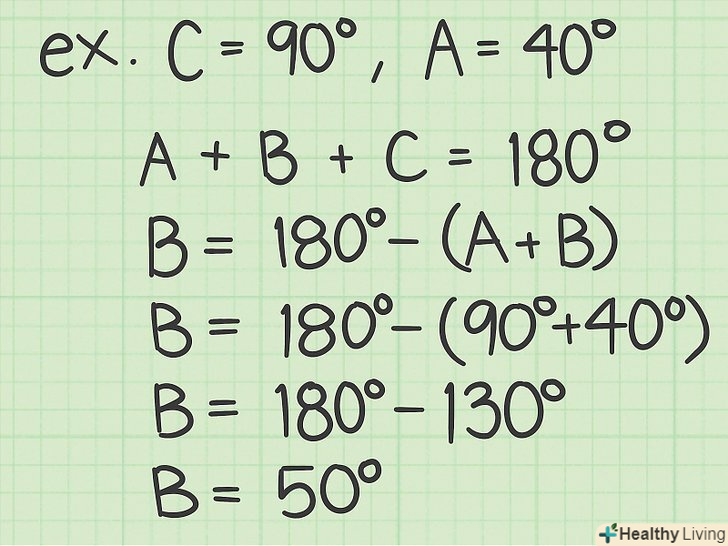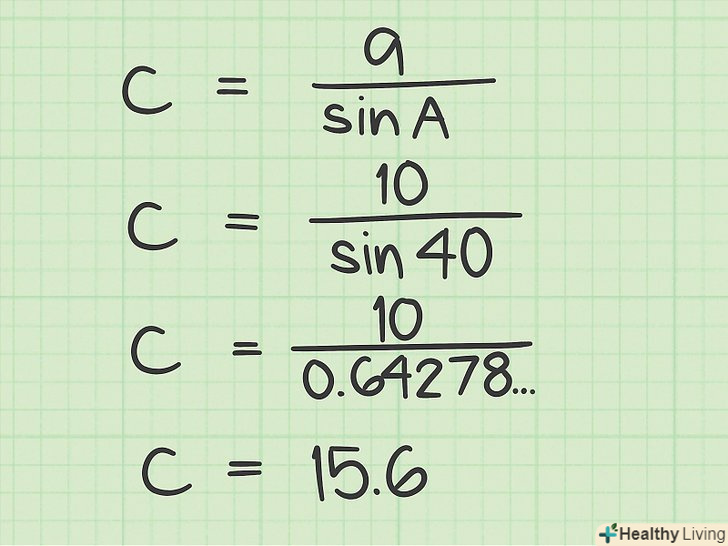Всі прямокутні трикутники мають один прямий кут (90 градусів), а протилежна йому сторона називається гіпотенузою.[1] гіпотенуза-найдовша сторона трикутника, і знайти її можна різними способами. У цій статті ми розповімо вам, як знайти гіпотенузу по теоремі Піфагора (коли відомі довжини двох інших сторін трикутника), по теоремі синусів (коли відомі довжина катета і кут) і в деяких окремих випадках (часто такі завдання зустрічаються на контрольних і тестах).
Кроки
Метод1З 3:
Теорема Піфагора
Метод1З 3:

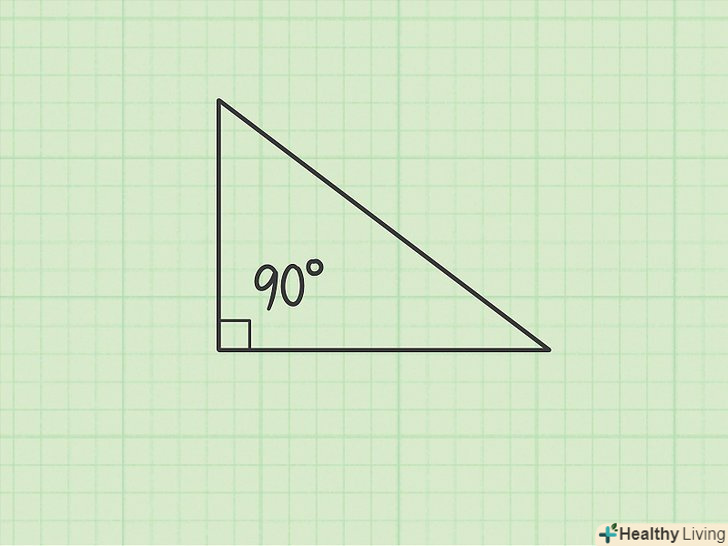
 Переконайтеся, що даний Вам трикутник є прямокутним, так як теорема Піфагора застосовна тільки до прямокутних трикутників.у прямокутних трикутниках один з трьох кутів завжди дорівнює 90 градусам.
Переконайтеся, що даний Вам трикутник є прямокутним, так як теорема Піфагора застосовна тільки до прямокутних трикутників.у прямокутних трикутниках один з трьох кутів завжди дорівнює 90 градусам.- Прямий кут в прямокутному трикутнику позначається значком у вигляді квадрата.
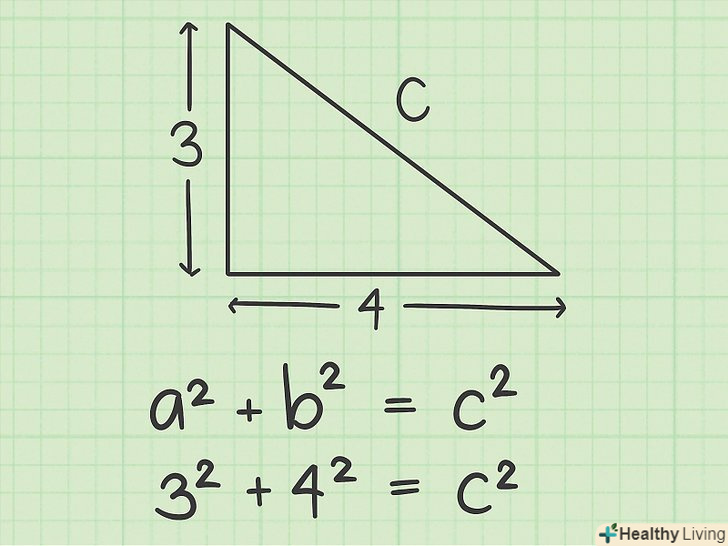
 Позначте сторони трикутника. катети позначте як «А» і «b» (катети — сторони, що перетинаються під прямим кутом), а гіпотенузу — як " с " (гіпотенуза — найбільша сторона прямокутного трикутника, що лежить навпроти прямого кута). Потім підставте дані вам значення в формулу.
Позначте сторони трикутника. катети позначте як «А» і «b» (катети — сторони, що перетинаються під прямим кутом), а гіпотенузу — як " с " (гіпотенуза — найбільша сторона прямокутного трикутника, що лежить навпроти прямого кута). Потім підставте дані вам значення в формулу.- Наприклад, катети трикутника рівні 3 і 4. У цьому випадку а = 3, b = 4, а формула виглядає так:32 + 42 = c2.
 Зведіть в квадрат значення катетів (»a «і»b").для цього просто помножте число саме на себе:
Зведіть в квадрат значення катетів (»a «і»b").для цього просто помножте число саме на себе:- Якщо a = 3, ТО a2 = 3 x 3 = 9. Якщо b = 4, то b2 = 4 x 4 = 16.
- Підставте ці значення в формулу:9 + 16 = с2.
 Складіть знайдені квадрати катетів (a2 і b2), щоб обчислити квадрат значення гіпотенузи (з2).
Складіть знайдені квадрати катетів (a2 і b2), щоб обчислити квадрат значення гіпотенузи (з2).- У нашому прикладі9 + 16 = 25, тому З2 = 25.
 Знайдіть квадратний корінь з2 .використовуйте калькулятор, щоб витягти квадратний корінь зі знайденого значення. Так ви обчислите гіпотенузу трикутника.
Знайдіть квадратний корінь з2 .використовуйте калькулятор, щоб витягти квадратний корінь зі знайденого значення. Так ви обчислите гіпотенузу трикутника.- У нашому прикладіЗ2 = 25 . Квадратний корінь з 25 дорівнює 5 (так як 5 х 5 = 25, тому √25 = 5). Це означає, що гіпотенуза С = 5.
Метод2 З 3:
Приватні випадки
Метод2 З 3:
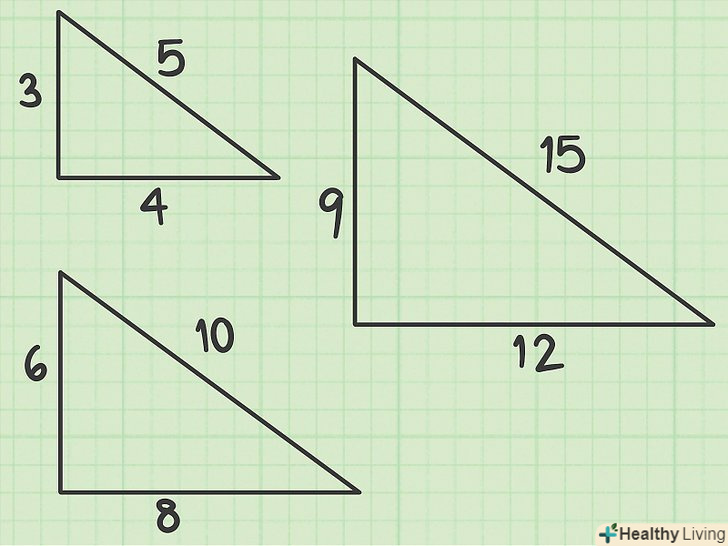
 Визначення піфагорової трійки. піфагорова трійка - це три числа — довжини трьох сторін), які задовольняють теоремі Піфагора. Дуже часто трикутники з такими сторонами наводяться в підручниках і на тестах. Якщо ви запам'ятаєте перші кілька піфагорових трійок, ви заощадите багато часу на тестах або іспитах, тому що зможете обчислити гіпотенузу, просто поглянувши на довжини катетів.[4]
Визначення піфагорової трійки. піфагорова трійка - це три числа — довжини трьох сторін), які задовольняють теоремі Піфагора. Дуже часто трикутники з такими сторонами наводяться в підручниках і на тестах. Якщо ви запам'ятаєте перші кілька піфагорових трійок, ви заощадите багато часу на тестах або іспитах, тому що зможете обчислити гіпотенузу, просто поглянувши на довжини катетів.[4]- Перша піфагорова Трійка:3-4-5 (32 + 42 = 52, 9 + 16 = 25). Якщо дано трикутник з катетами 3 і 4, то ви можете з упевненістю заявити, що гіпотенуза дорівнює 5 (без необхідності робити будь-які розрахунки).
- Піфагорові трійки працюють навіть в тому випадку, коли числа помножені або розділені на один коефіцієнт. Наприклад, якщо катети рівні6 і 8, гіпотенуза дорівнює 10 (62 + 82 = 102, 36 + 64 = 100). Те ж саме вірно для 9-12-15 і навіть для 1,5-2-2,5.
- Друга піфагорова Трійка:5-12-13 (52 + 122 = 132, 25 + 144 = 169). Також до цієї трійки відносяться, наприклад, числа 10-24-26 і 2,5-6-6,5.
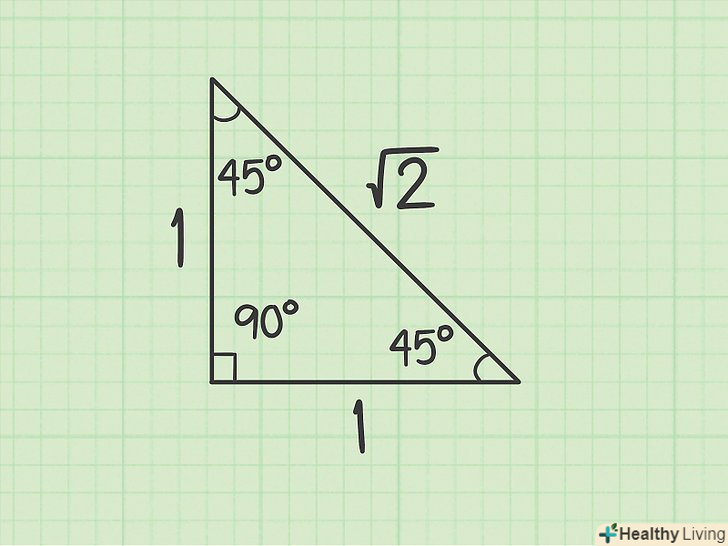
 Рівнобедрений прямокутний трикутник.це такий трикутник, кути якого рівні 45,45 і 90 градусам. Співвідношення між сторонами цього трикутника дорівнює 1:1:√2. Це означає, що гіпотенуза в такому трикутнику дорівнює добутку катета і квадратного кореня з 2.
Рівнобедрений прямокутний трикутник.це такий трикутник, кути якого рівні 45,45 і 90 градусам. Співвідношення між сторонами цього трикутника дорівнює 1:1:√2. Це означає, що гіпотенуза в такому трикутнику дорівнює добутку катета і квадратного кореня з 2.- Щоб обчислити гіпотенузу такого трикутника, просто помножте довжину будь-якого катета на √2.[5]
- Це співвідношення особливо зручно, коли в задачах замість числових значень даються змінні.
 Половина рівностороннього прямокутного трикутника.це такий трикутник, кути якого рівні 30,60 і 90 градусам. Співвідношення між сторонами цього трикутника одно 1:√3:2або Х:х√3: 2х. Щоб знайти гіпотенузу в такому трикутнику виконайте одну з наступних дій:[6]
Половина рівностороннього прямокутного трикутника.це такий трикутник, кути якого рівні 30,60 і 90 градусам. Співвідношення між сторонами цього трикутника одно 1:√3:2або Х:х√3: 2х. Щоб знайти гіпотенузу в такому трикутнику виконайте одну з наступних дій:[6]- Якщо вам дано короткий катет (протилежний кутку в 30 градусів), просто помножте довжину цього катета на 2, щоб знайти довжину гіпотенузи. Наприклад, якщо короткий катет дорівнює4, то гіпотенуза дорівнює 8.
- Якщо вам дано довгий катет (протилежний кут в 60 градусів), просто помножте довжину цього катета на2/√3, щоб знайти довжину гіпотенузи. Наприклад, якщо короткий катет дорівнює 4, то гіпотенуза дорівнює 4,62.
Метод3 З 3:
Теорема синусів
Метод3 З 3:
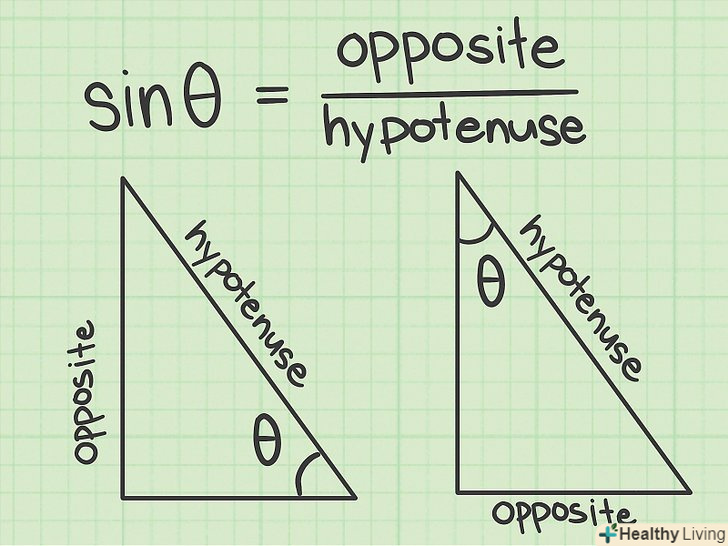
 Зрозумійте, що означає "синус".Синус, косинус і тангенс кута-це основні тригонометричні функції, що зв'язують кути і сторони в прямокутному трикутнику. Синус кута дорівнює відношенню протилежної сторони до гіпотенузи. Позначається синус як Sin .[7]
Зрозумійте, що означає "синус".Синус, косинус і тангенс кута-це основні тригонометричні функції, що зв'язують кути і сторони в прямокутному трикутнику. Синус кута дорівнює відношенню протилежної сторони до гіпотенузи. Позначається синус як Sin .[7] Навчіться обчислювати синус. щоб обчислити синус, на калькуляторі знайдіть клавішу Sin , натисніть її, а потім введіть значення кута. У деяких калькуляторах спочатку потрібно натиснути клавішу переходу до роботи з функціями, а потім натиснути клавішу Sin. Тому поекспериментуйте з калькулятором або перевірте його документацію.
Навчіться обчислювати синус. щоб обчислити синус, на калькуляторі знайдіть клавішу Sin , натисніть її, а потім введіть значення кута. У деяких калькуляторах спочатку потрібно натиснути клавішу переходу до роботи з функціями, а потім натиснути клавішу Sin. Тому поекспериментуйте з калькулятором або перевірте його документацію.- Щоб знайти синус кута в 80 градусів, натисніть "sin», «8», «0», «=» або натисніть" 8», «0», « sin», " = " (відповідь: -0,9939).
- Ви також можете знайти онлайн-калькулятор, ввівши в пошуковій системі " обчислення синуса "(без лапок).[8]
 Запам'ятайте теорему синусів.Теорема синусів є корисним інструментом для обчислення кутів і сторін будь-якого трикутника. Зокрема, вона допоможе вам знайти гіпотенузу прямокутного трикутника, якщо вам дано катет і кут, відмінний від прямого. Згідно з теоремою синусів, в будь-якому трикутнику зі сторонами A, B, C і кутами A, B, C вірно рівність A /sin a = B /sin b = C /sin з.[9]
Запам'ятайте теорему синусів.Теорема синусів є корисним інструментом для обчислення кутів і сторін будь-якого трикутника. Зокрема, вона допоможе вам знайти гіпотенузу прямокутного трикутника, якщо вам дано катет і кут, відмінний від прямого. Згідно з теоремою синусів, в будь-якому трикутнику зі сторонами A, B, C і кутами A, B, C вірно рівність A /sin a = B /sin b = C /sin з.[9]- Теорема синусів застосовується до будь-яких трикутників, а не тільки до прямокутних (але тільки в прямокутному трикутнику є гіпотенуза).
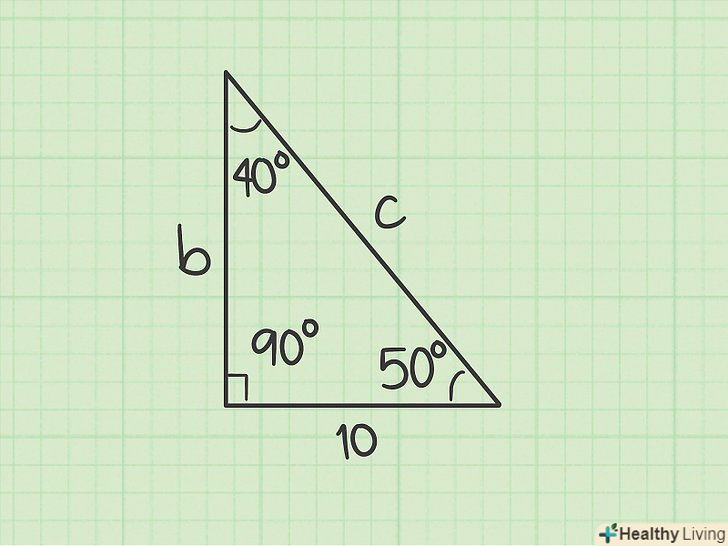
 Позначте сторони трикутника через «а» (відомий катет), «b» (невідомий катет), «с» (гіпотенуза).потім позначте кути трикутника через "а «(навпроти катета» а«),» В «(навпроти катета» b«),» С" (навпроти гіпотенузи).
Позначте сторони трикутника через «а» (відомий катет), «b» (невідомий катет), «с» (гіпотенуза).потім позначте кути трикутника через "а «(навпроти катета» а«),» В «(навпроти катета» b«),» С" (навпроти гіпотенузи). Знайдіть третій кут. якщо вам дано один з гострих кутів прямокутного трикутника (А або В), а другий кут завжди дорівнює 90 градусам (С = 90), то третій кут обчислюється за формулою 180 - (90 + А) = B (пам'ятайте, що сума кутів в будь-якому трикутнику дорівнює 180 градусам). При необхідності рівняння можна змінити і так: 180 - (90 + B) = A.
Знайдіть третій кут. якщо вам дано один з гострих кутів прямокутного трикутника (А або В), а другий кут завжди дорівнює 90 градусам (С = 90), то третій кут обчислюється за формулою 180 - (90 + А) = B (пам'ятайте, що сума кутів в будь-якому трикутнику дорівнює 180 градусам). При необхідності рівняння можна змінити і так: 180 - (90 + B) = A.- Наприклад, якщо кутA = 40 градусам, то B = 180 - (90 + 40) = 180 - 130 = 50 градусів.

- У нашому прикладі припустимо, що катет а = 10, а кути рівні C = 90, A = 40, в = 50.
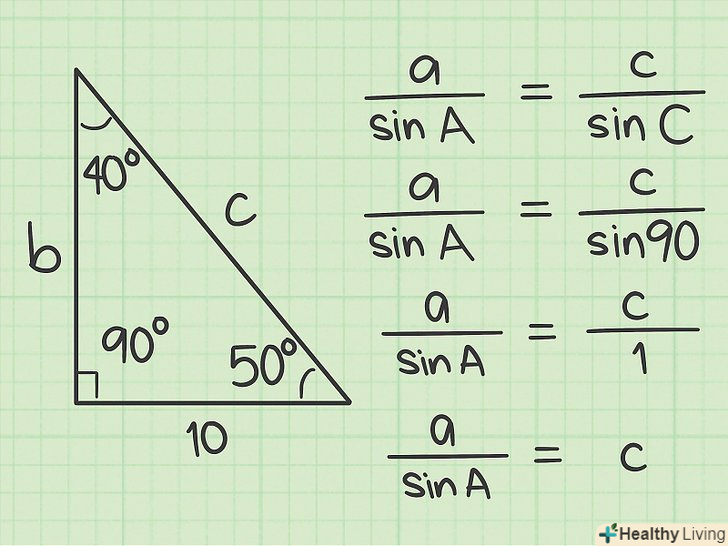
 Підставте дані і знайдені значення в теорему синусів, щоб знайти гіпотенузу:Катет «а»/синус кута «A» = гіпотенуза «с»/синус кута «С». При цьому sin 90 = 1. Таким чином, рівняння спрощується до: А/sinA = с/1або С = а/sinA.
Підставте дані і знайдені значення в теорему синусів, щоб знайти гіпотенузу:Катет «а»/синус кута «A» = гіпотенуза «с»/синус кута «С». При цьому sin 90 = 1. Таким чином, рівняння спрощується до: А/sinA = с/1або С = а/sinA. Розділіть довжину катета «а «на синус кута» а", щоб знайти довжину гіпотенузи.для цього спочатку знайдіть синус кута, а потім виконайте поділ. Або ви можете скористатися калькулятором, ввівши 10/(sin40) або 10/(40sin) (Не забудьте про дужки).
Розділіть довжину катета «а «на синус кута» а", щоб знайти довжину гіпотенузи.для цього спочатку знайдіть синус кута, а потім виконайте поділ. Або ви можете скористатися калькулятором, ввівши 10/(sin40) або 10/(40sin) (Не забудьте про дужки).- У нашому прикладі sin 40 = 0,64278761, а с =10/0,64278761 = 15,6.
Джерела
- ↑ Http://www.mathsisfun.com/definitions/hypotenuse.html
- ↑ Http://mathematica.ludibunda.ch/pythagoras6.html
- ↑ Http://www.wikihow.com/Use-the-Pythagorean-Theorem
- ↑ Http://www.dummies.com/how-to/content/working-with-pythagorean-triple-triangles.html
- ↑ Http://www.regentsprep.org/regents/math/algtrig/att2/ltri45.htm
- ↑ Http://www.dummies.com/how-to/content/identifying-the-30-60-90-degree-triangle.html
- ↑ Https://www.mathsisfun.com/definitions/sine.html
- ↑ Http://www.rapidtables.com/calc/math/Sin_Calculator.htm
- ↑ Http://www.mathsisfun.com/algebra/trig-sine-law.html