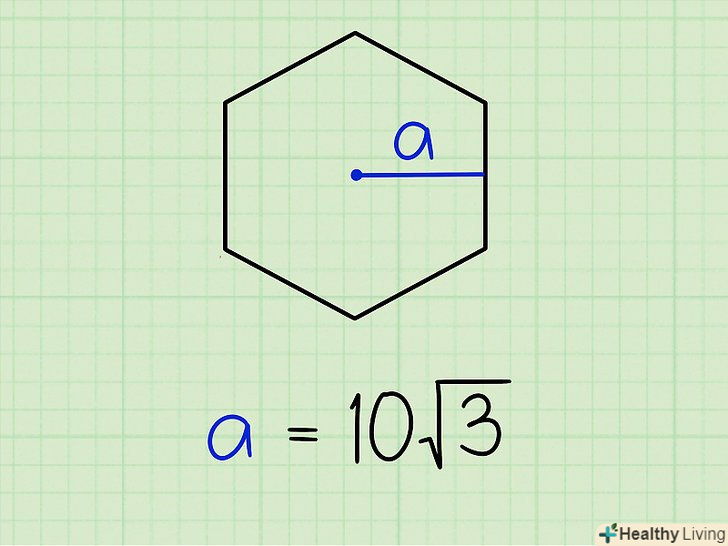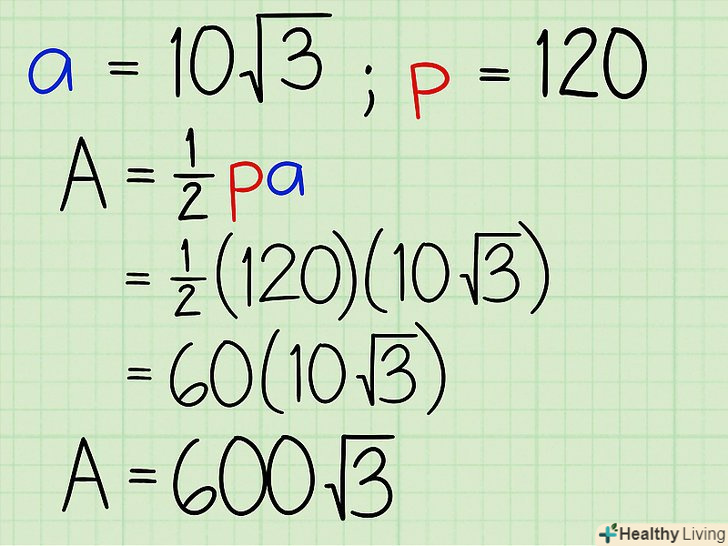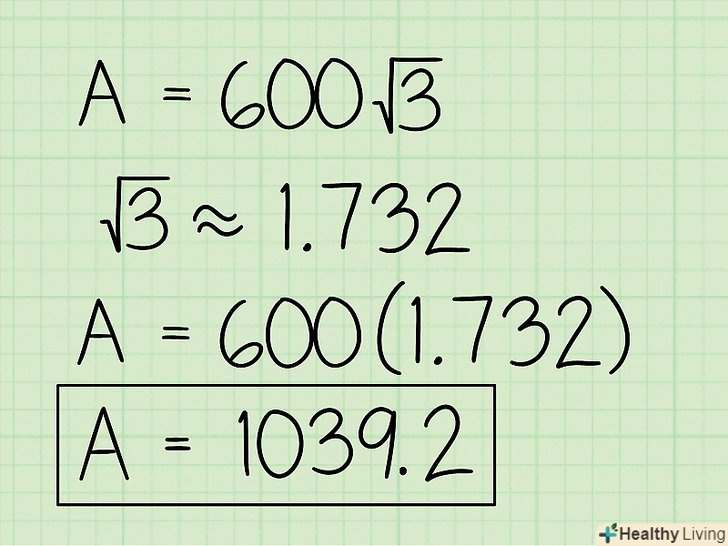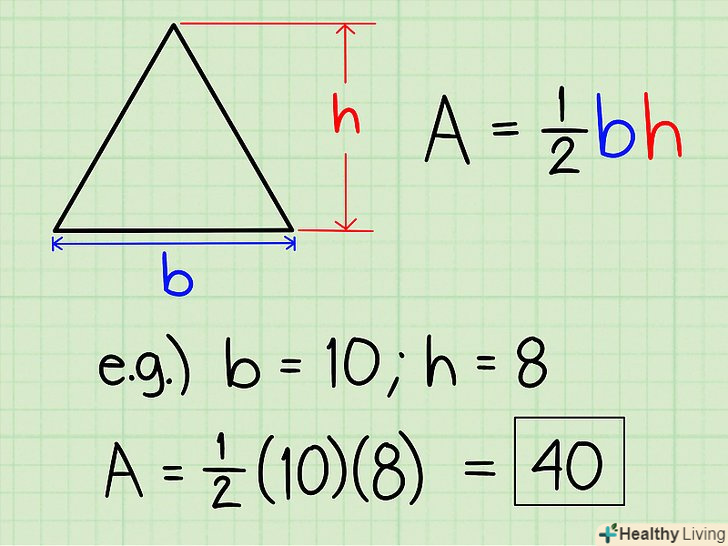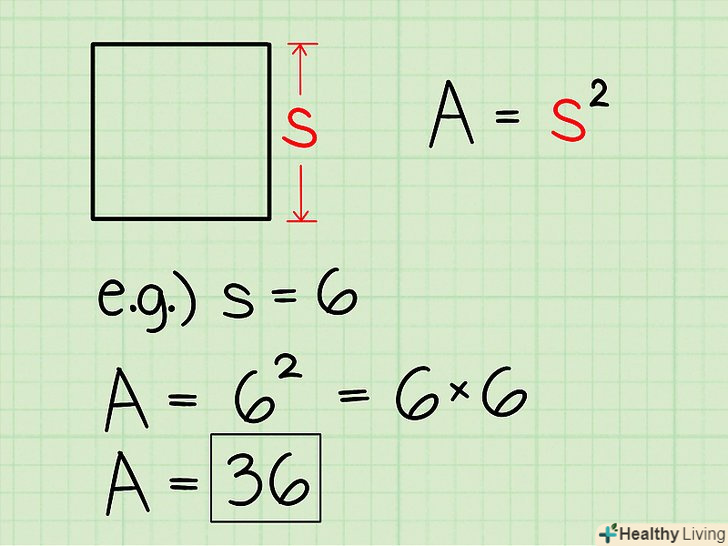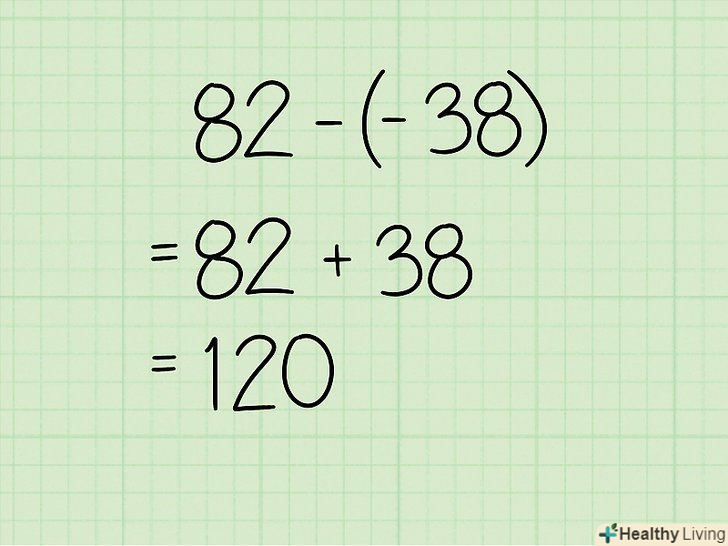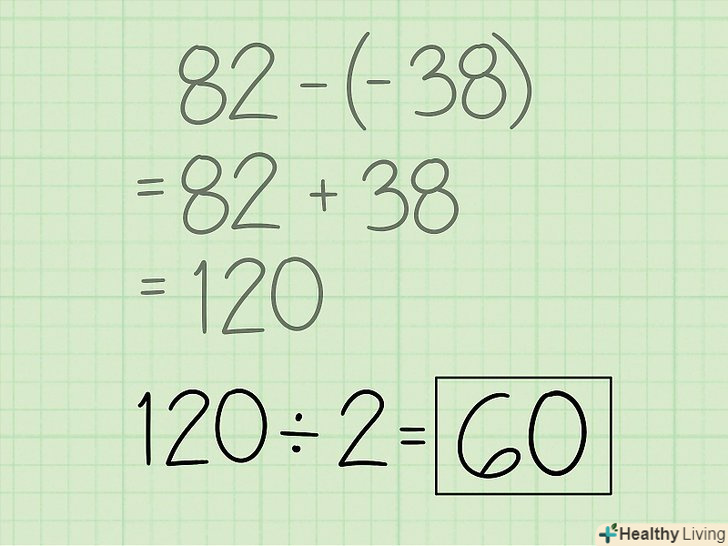Як знайти площу багатокутника-

Дуже легко обчислити площу правильного трикутника (це багатокутник!) і дуже непросто зробити це в разі неправильного одинадцятикутника (це теж багатокутник!). Дана стаття розповість вам, як обчислювати площу різних багатокутників.

Метод1З 3:

Обчислення площі правильного багатокутника з апофеме

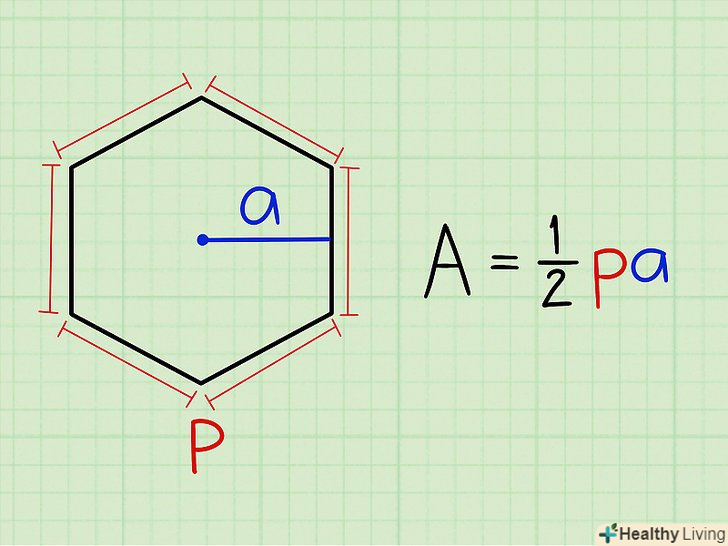
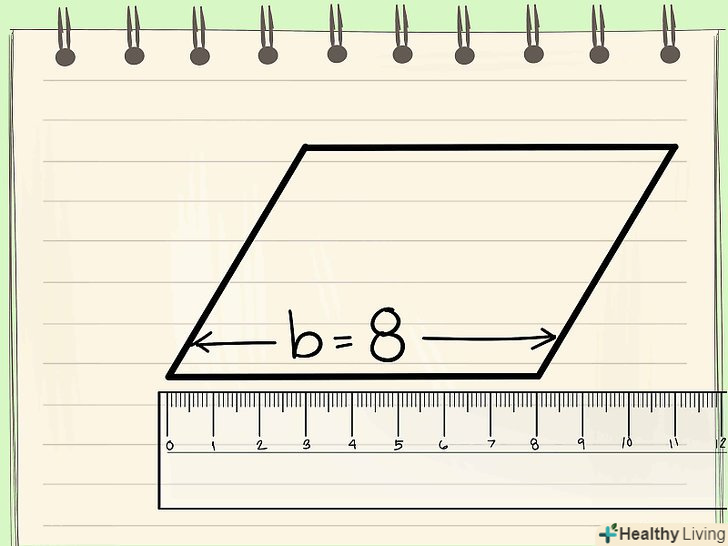
Формула для знаходження площі правильного багатокутника: площа = 1/2 х периметр х апофема.
- Периметр-сума сторін багатокутника.
- Апофема-відрізок, що з'єднує центр багатокутника і середину будь-якої з його сторін (апофема перпендикулярна стороні).
Знайдіть апофему.вона, як правило, дана в умові завдання. Наприклад, дано шестикутник, апофема якого дорівнює 10√3.
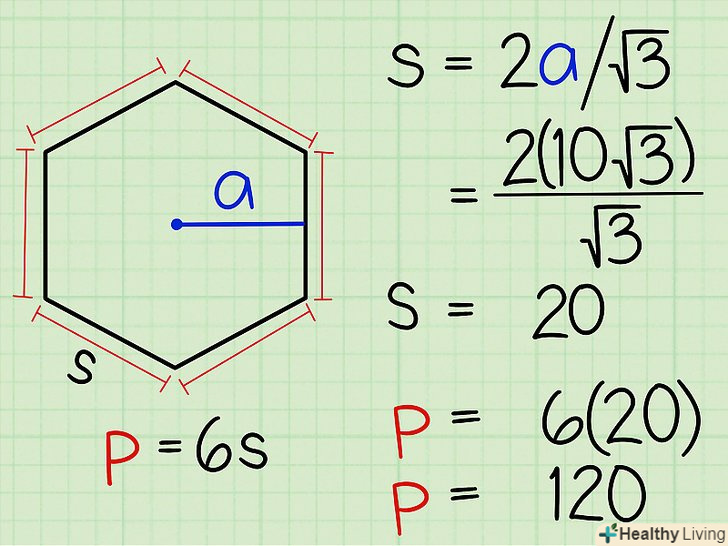
Знайдіть периметр.якщо периметр не дано в умові завдання, то його можна знайти за відомою апофеме.
- Шестикутник можна розбити на 6 рівносторонніх трикутників. Апофема ділить одну сторону навпіл, створюючи прямокутний трикутник з кутами 30-60-90 градусів.
- У прямокутному трикутнику сторона, протилежна куту в 60 градусів, дорівнює x√3; куту в 30 градусів дорівнює «х»; куту 90 градусів дорівнює 2x. якщо значення боку x√3 дорівнює 10√3, то х = 10.
- " х " - це половина довжини підстави трикутника. Подвійте її і знайдете повну довжину підстави. У нашому прикладі підстава трикутника дорівнює 20 одиницям. У свою чергу підстава трикутника є сторона шестикутника. Таким чином, периметр шестикутника дорівнює 20 х 6 = 120.
Підставте значення апофеми і периметра в формулу. у нашому прикладі:
- Площа = 1/2 х 120 х 10√3
- Площа = 60 х 10√3
- Площа = 600√3
Спростіть відповідь.можливо, вам доведеться записати відповідь у вигляді десяткового дробу (тобто позбутися від кореня). За допомогою калькулятора знайдіть √3 і отримане число помножте на 600: √3 х 600 = 1039,2. Це ваша остаточна відповідь.

Метод2 З 3:

Обчислення площі правильного багатокутника за іншими формулами

Знайдіть площу трикутника . Формула: площа = 1/2 х підстава х висота.
- Якщо вам дано трикутник з підставою 10 і висотою 8, то його площа = 1/2 х 8 х 10 = 40.
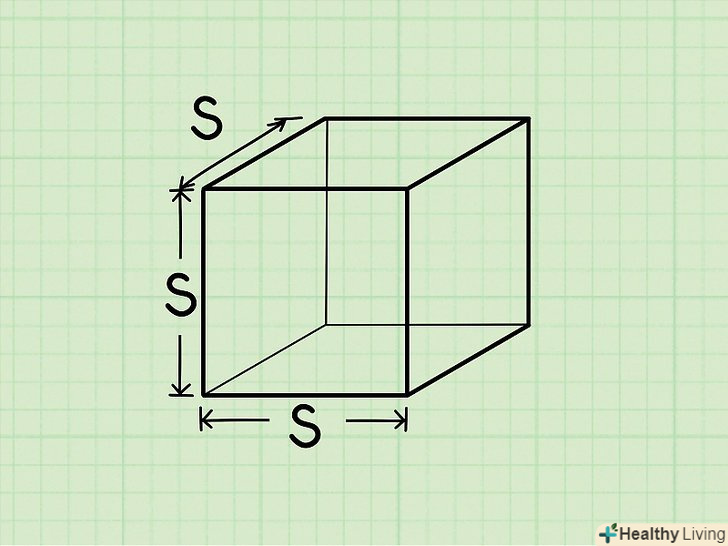
Знайдіть площу квадрата.щоб знайти площу квадрата, просто зведіть в квадрат довжину однієї його сторони. Якщо помножити підставу квадрата на його висоту, ми отримаємо ту ж відповідь, так як підстава і висота рівні.
- Якщо сторона квадрата дорівнює 6, то його площа = 6 х 6 = 36.
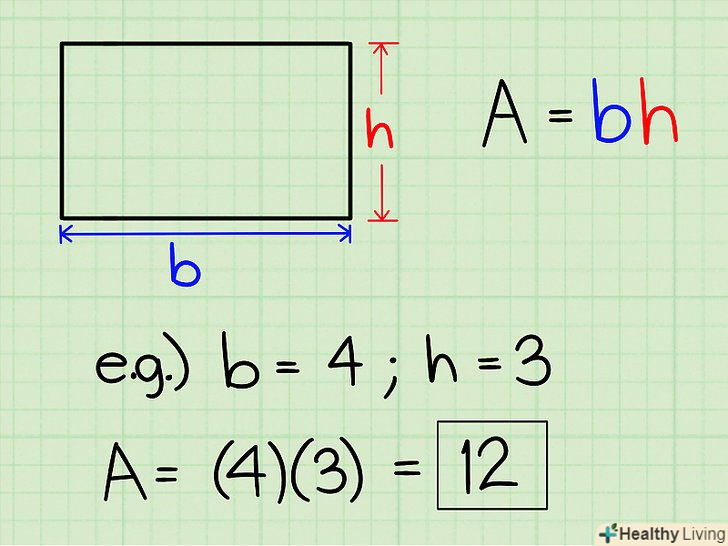
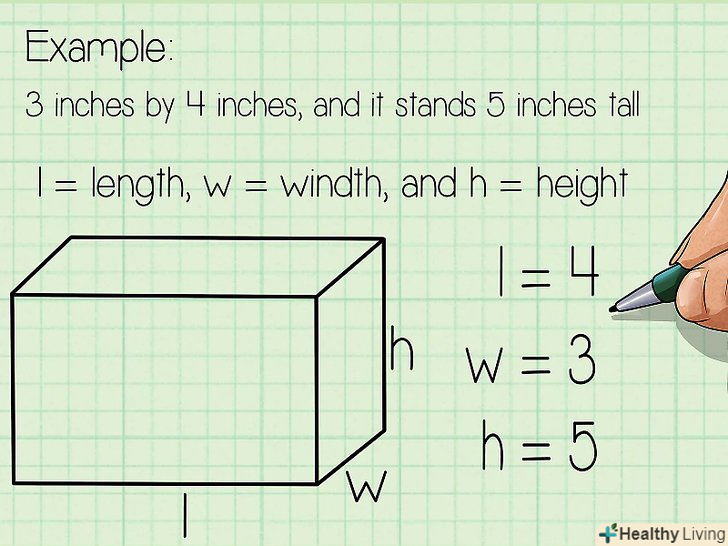
Знайдіть площу прямокутника . Формула: площа = довжина х ширина.
- Якщо довжина прямокутника дорівнює 4, а ширина дорівнює 3, то його площа = 4 х 3 = 12.
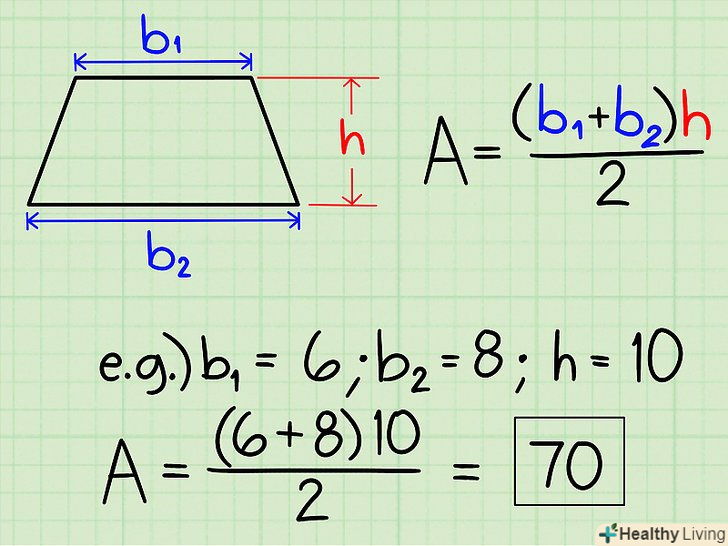
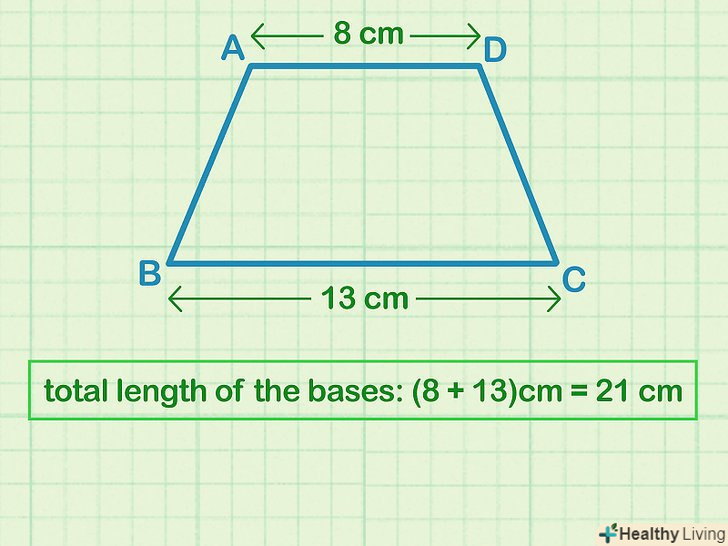
Знайдіть площу трапеції . Формула: Площа = [(підстава1 + підстава2) х Висота] / 2.
- Наприклад, дана трапеція з підставами 6 і 8 і висотою 10. Її площа = [(6 + 8)•10]/2 = (14 х 10)/2 = 140/2 = 70.

Метод3 З 3:

Обчислення площі неправильного багатокутника

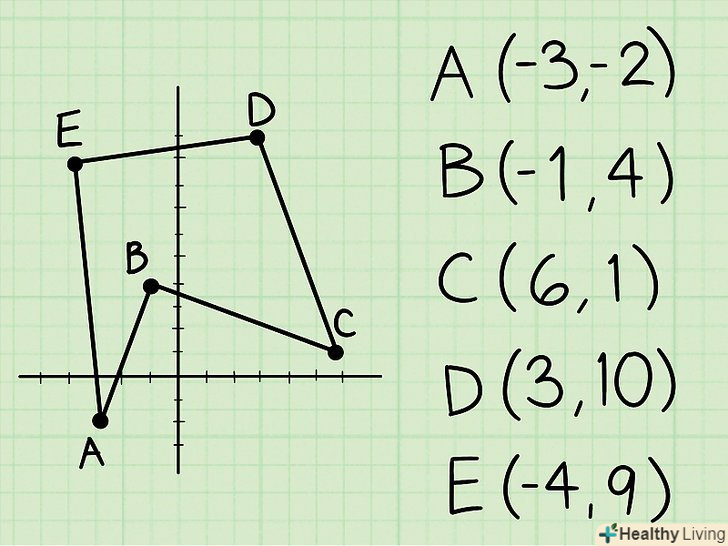
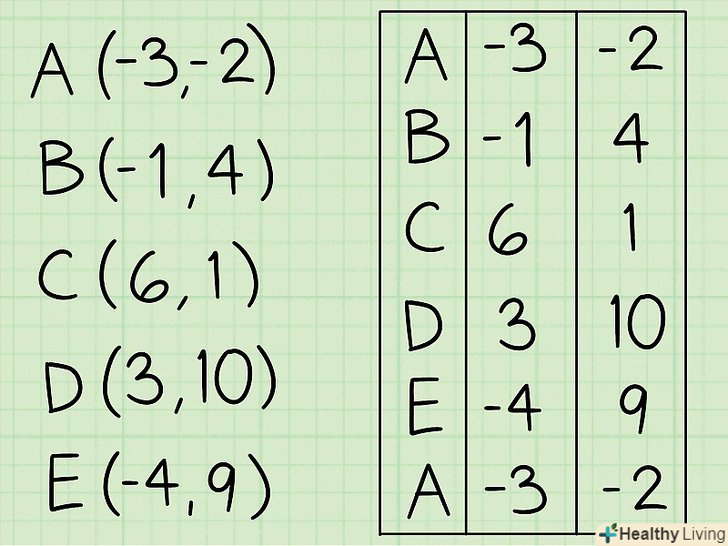
Використовуйте координати вершин неправильного багатокутника.знаючи координати вершин, можна визначити площу неправильного багатокутника.
Зробіть таблицю.запишіть координати вершин (х,у) (вершини вибирати послідовно в напрямку проти годинникової стрілки). В кінці списку ще раз напишіть координату першої вершини.
Помножте значення координати» х «першої вершини на значення координати» у " другої вершини (і так далі). складіть результати (в нашому прикладі сума дорівнює 82).
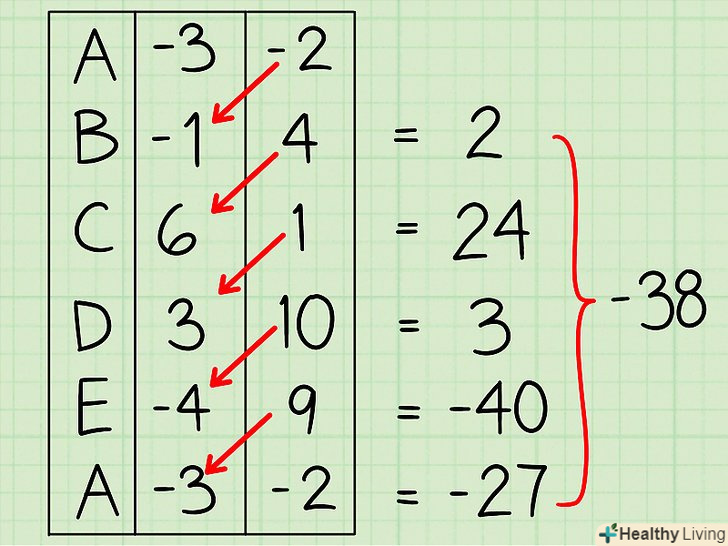
Помножте значення координати» у «перший вершини на значення координати» х " другої вершини (і так далі). складіть результати (в нашому прикладі сума дорівнює -38).
Відніміть суму, отриману в кроці 4, з суми, отриманої в кроці 3. у нашому прикладі: (82) - (-38) = 120.
Розділіть отриманий результат на 2, щоб знайти площу багатокутника: S=120/2 = 60 (квадратних одиниць).

Поради

Якщо ви записуєте координати вершин у напрямку за годинниковою стрілкою, ви отримаєте негативну площу. Таким чином, це можна використовувати для опису циклу або послідовності даного набору вершин, що формують багатокутник.
Дана формула знаходить площу з урахуванням форми багатокутника. Якщо багатокутник має форму цифри 8, то необхідно з площі з вершинами проти годинникової стрілки відняти площу з вершинами за годинниковою стрілкою.