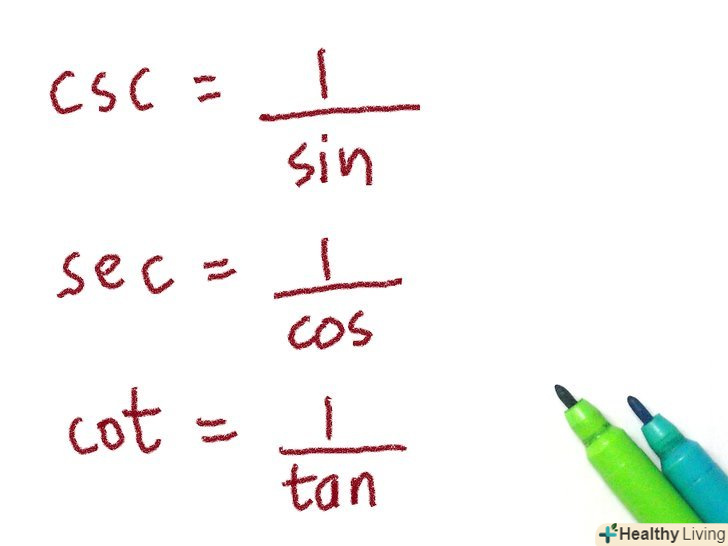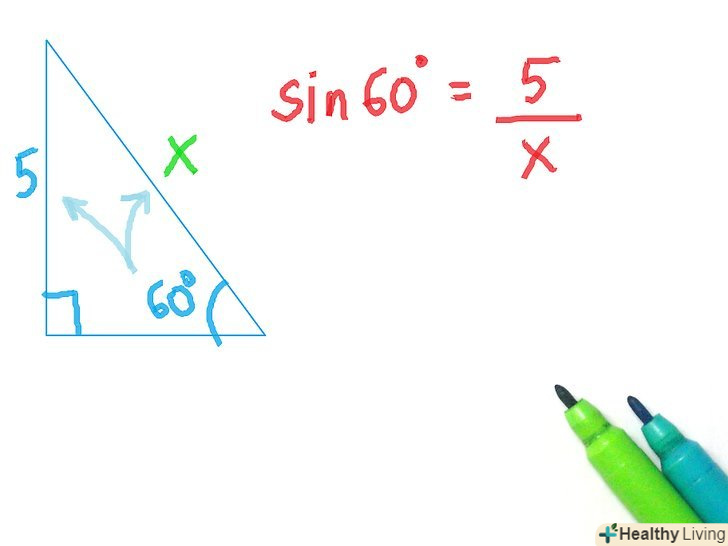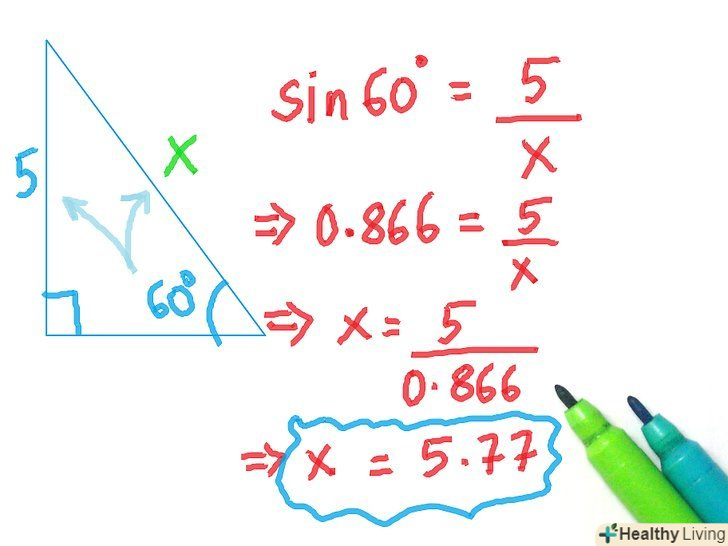Тригонометрія прямого кута-це дуже корисна річ при розрахунку трикутників, а також - це фундаментальна частина тригонометрії, як науки в цілому. Зазвичай, тригонометрія прямого кута - це перша зустріч студентів з тригонометрією, і, це часто приводить їх в замішання з першого разу. Наступні кроки роз'яснять основні тригонометричні відносини, а також, як їх використовувати.
Кроки
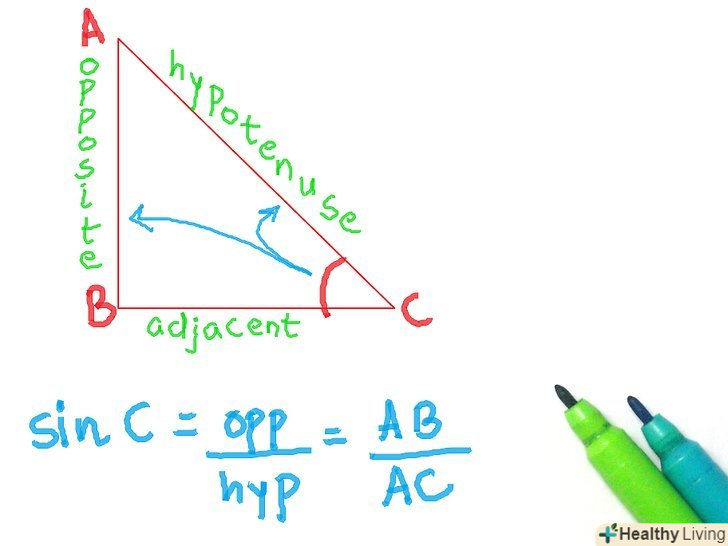
- Запам'ятайте 6 основних тригонометричних відносин. Запам'ятайте наступне:
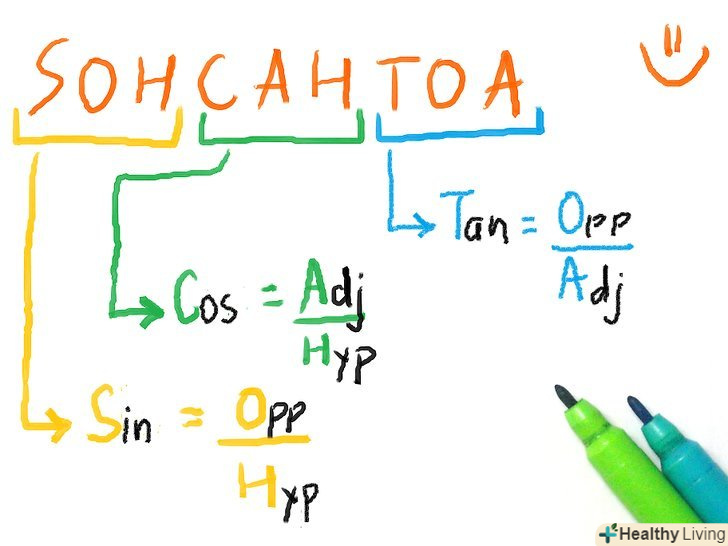
- Синус
- Скорочено " sin "
- Протилежна сторона / гіпотенуза
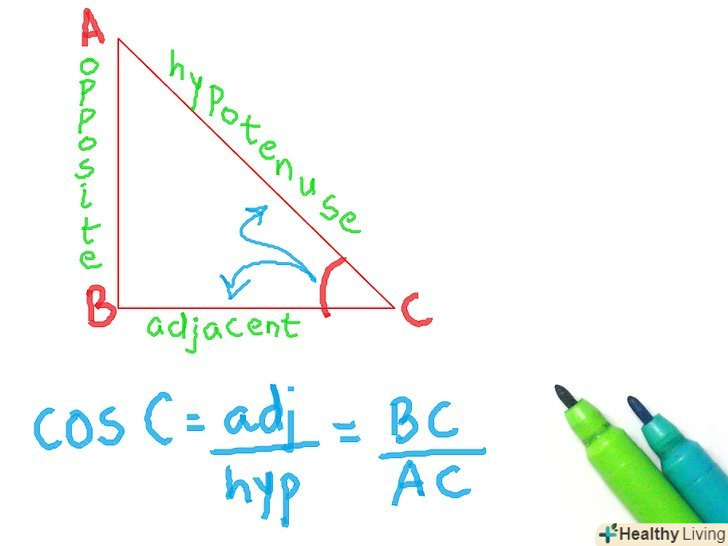
- Косинус
- Скорочено " cos»
- Прилегла сторона / гіпотенуза
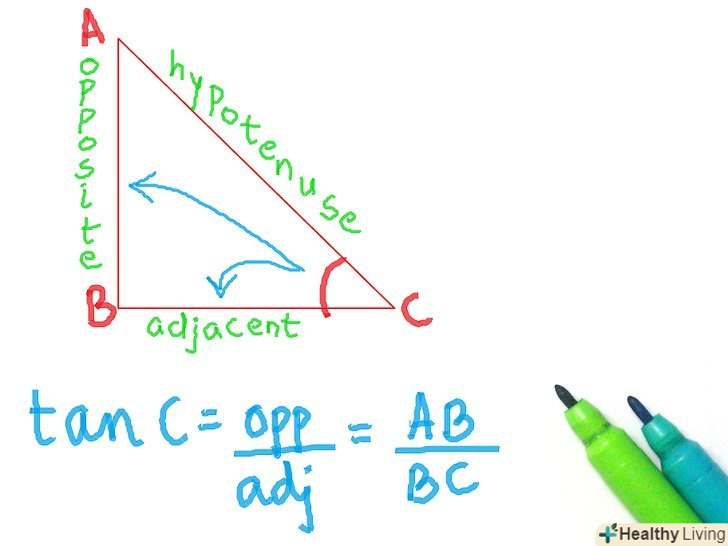
- Тангенс
- Скорочено " tan "
- Протилежна сторона / прилегла сторона
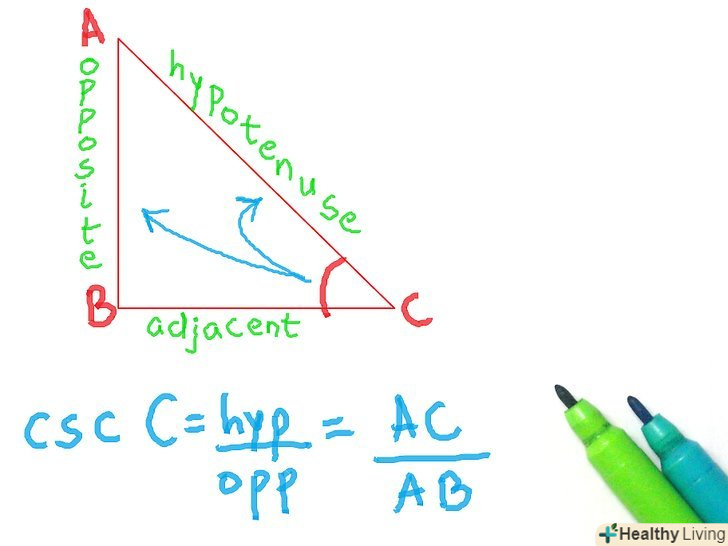
- Косеканс
- Скорочено " csc "
- Гіпотенуза / протилежна сторона
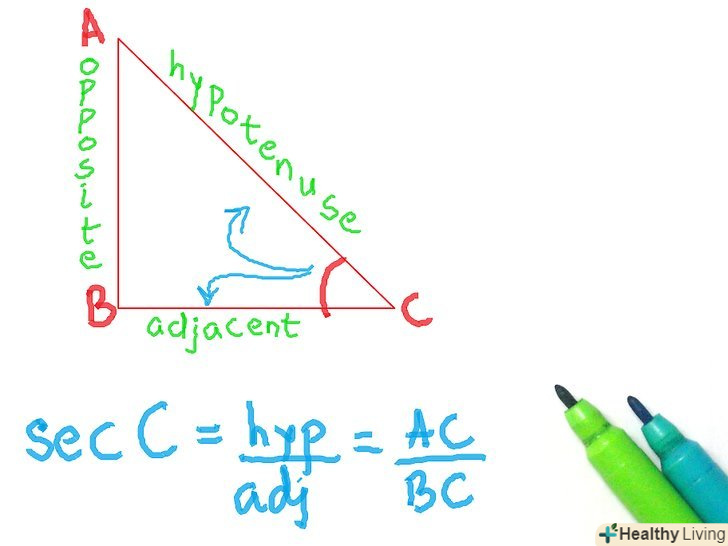
- Секанс
- Скорочено " sec»
- Гіпотенуза / прилегла сторона
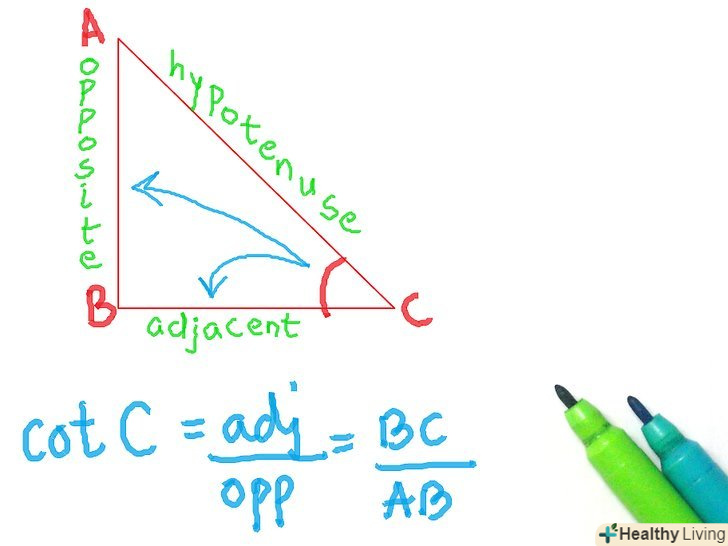
- Котангенс
- Скорочено " cot "
- Прилегла сторона / протилежна сторона
- Синус
- Подивіться на малюнки.не переживайте, якщо з першого погляду вас все введе в замішання, і не бійтеся, що не зможете все це запам'ятати. Це зовсім не складно, якщо ви запам'ятаєте приклади:
- Дані абревіатури завжди використовуються в тригонометричних функціях. Вам ніколи не доведеться писати цілком назви тригонометричних функцій. Коли ви бачите абревіатуру, то у вас в голові має спливати назва тригонометричної функції. Зауважте, що у всіх випадках, крім " csc "(косеканс), абревіатури збігаються з першими трьома літерами назвами. "Csc « - це виняток, тому що абревіатура» cos" вже використовується для позначення косинуса. Тому, замість них використовуються перші три приголосні літери.
- Ви можете запам'ятати перші три співвідношення за допомогою слова "Sohcahtoa". Просто запам'ятайте його, як ім'я якогось правителя ацтеків. Запам'ятайте, як точно вимовляється це слово. Це перші літери слів» s « - синус (sine),» o « - протилежна сторона (opposite),» h« - гіпотенуза (hypotenuse);» с " - косинус (cosine), «a» - прилегла сторона (adjacent), «h» - гіпотенуза (hypotenuse);«t» - тангенс (tangent), «o» - протилежна сторона (opposite), «a» - прилегла сторона (adjacent). Запам'ятайте, що коли ви вставляєте слово між будь-якими словами, які не є тригонометричними відносинами (наприклад, протилежна сторона і гіпотенуза, не cos і прилегла сторона), після назви будь-який з тригонометричних функцій - це співвідношення.
- Залишилися три функції-це просто зворотні функції перших трьох (не перевернуті). Пам'ятайте, що у всього без префікса «co» - зворотна функція з префіксом, а у всього з префіксом «co» - зворотна функція без префікса. Таким чином, косеканс, секанс і котангенс – це зворотні функції синуса, косинуса і тангенса. Наприклад котангенс-це відношення прилеглої сторони до протилежної сторони.
- Дані абревіатури завжди використовуються в тригонометричних функціях. Вам ніколи не доведеться писати цілком назви тригонометричних функцій. Коли ви бачите абревіатуру, то у вас в голові має спливати назва тригонометричної функції. Зауважте, що у всіх випадках, крім " csc "(косеканс), абревіатури збігаються з першими трьома літерами назвами. "Csc « - це виняток, тому що абревіатура» cos" вже використовується для позначення косинуса. Тому, замість них використовуються перші три приголосні літери.
-
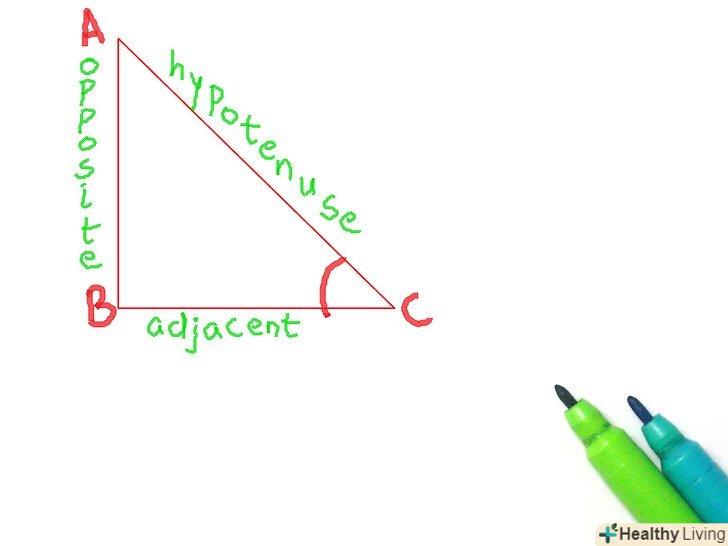
Запам'ятайте, як називаються сторони трикутника.швидше за все, Ви знаєте де знаходиться гіпотенуза, але у вас можуть виникнути сумніви з приводу протилежної і прилеглої сторін. Подивіться на зображення: ось так правильно розставляти сторони, якщо ви використовуєте кут С.якщо ви хочете використовувати кут а, то сторони поміняються місцями на зображенні.
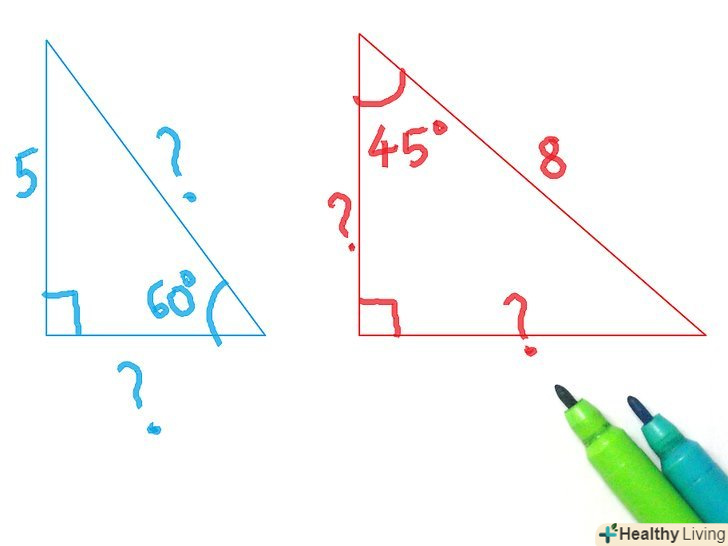
- Зрозумійте, що таке тригонометричні функції і для чого вони потрібні. коли прямокутний трикутник був відкритий, було також відкрито, що якщо у вас є два рівних прямокутних трикутника (тобто з рівними кутами), то якщо ви поділите одну сторону на іншу і зробите те ж саме з відповідними сторонами іншого трикутника, то результати будуть однаковими. Тригонометричні функції дозволяли знайти співвідношення для будь-якого даного кута. Назви сторін також були придумані, щоб легше бувальщина визначити, які кути використовувати. Ви можете використовувати тригонометричні функції, щоб визначити довжину сторони, при відомій стороні і вугіллі або визначити величину кута при двох відомих сторонах.
-
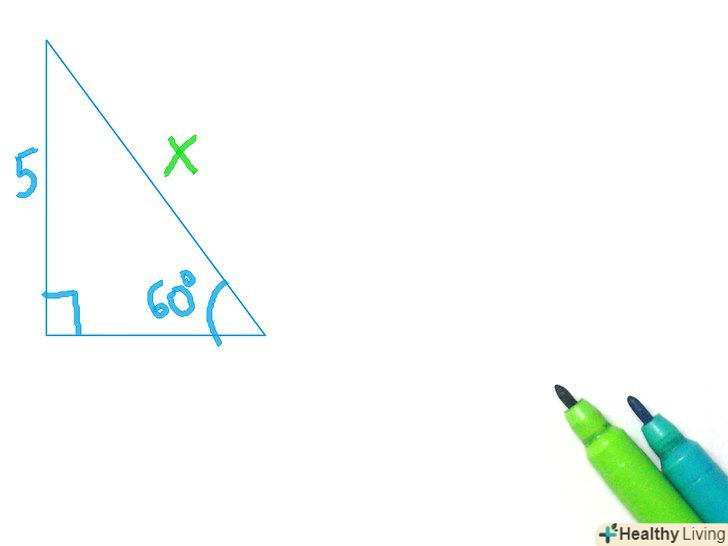
Визначте, що ви хочете знайти. Обзначьте невідому величину через «Х». Це допоможе вам пізніше скласти рівняння. Також, переконайтеся, що у вас є достатньо інформації, щоб вирішити трикутник. Вам необхідно знати величину кута і сторони або велечіни трьох сторін.
-
Встановіть співвідношення.позначте протилежну сторону, прилеглу сторону і гіпотенузу по відношенню до вибраного кута. Неважливо, чи є це позначення цифрою або «х» з попереднього кроку. Потім, випишіть сторони, які вам відомі, і які треба знайти. Не беручи до уваги косеканс, секанс і котангенс, визначте, яке співвідношення містить обидві сторони, які ви записали. Не використовуйте зворотні функції, тому що їх зазвичай немає на панелі калькулятора. Навіть якщо і є можливість, то вам майже ніколи не доведеться користуватися ними, щоб вирішити прямокутний трикутник. Коли ви визначили, яке співвідношення використовувати, запишіть його? Використовуючи змінні і невідомі. Потім запишіть рівняння, використовуючи назви сторін (прилегла, протилежна, гіпотенуза). Перепишіть рівняння, підставляючи величини сторін / змінних в співвідношення.
-
Вирішіть рівняння.якщо змінна знаходиться поза тригонометричної функції (це означає, що ви вирішували через сторону), то висловіть Х, а потім підставте значення і вирішите на калькуляторі, А відповідь округлите до десятих. Якщо ваша змінна знаходиться з лівого боку рівняння (це означає, що ви вирішуєте через кут), то вам необхідно спростити рівняння з правого боку . Наприклад, якщо у вас є рівняння sin(x)=2/4, то ви можете спростити праву частину, щоб отримати 1/2, потім введіть в калькулятор "sin-1" (це зазвичай одна кнопка, яка йде другий за рахунком в тригонометричних функціях), а потім 1/2. Переконайтеся, що ваш калькулятор налаштований на правильну програму під час обчислень, тобто встановіть калькулятор на радіани, якщо хочете отримати відповідь в радіанах або на градуси, якщо хочете отримати відповідь в градусах, а якщо не знаєте, то встановіть на градуси. Величина Х - це величина шуканого кута або шуканої сторони.
Поради
- Величини sin і cos завжди знаходяться між -1 і 1, але тангенс може бути будь-якою величиною. Якщо ви отримуєте помилковий результат, обчислюючи тангенс, то цей результат буде або дуже маленьким, або дуже великим. Перевірте співвідношення і спробуйте ще раз. Можливо, треба поміняти сторони місцями, як, наприклад гіпотенуза/протилежна сторона для синуса.
- Sin-1 - це не те ж саме, що csc, cos-1 - це не те ж саме, що sec, а tan-1 - це не те ж саме, що cot. Перше-це зворотна функція, що позначає, що якщо ви підставите величини у відповідні співвідношення, то це дасть вам в результаті відповідні кути, друге-це зворотна функція, яка означає, що співвідношення перевернуто.
