Радіани і градуси-це дві одиниці виміру кутів. Повний кут (або коло) дорівнює 360°, що еквівалентно 2π радіан; обидва значення характеризують один «оборот по колу». Тому півоберта дорівнює 1π радіан або 180°. Заплуталися? Тоді прочитайте цю статтю і навчитеся конвертувати градуси в радіани.
Кроки
 Запишіть градуси, які ви хочете перетворити в радіани.
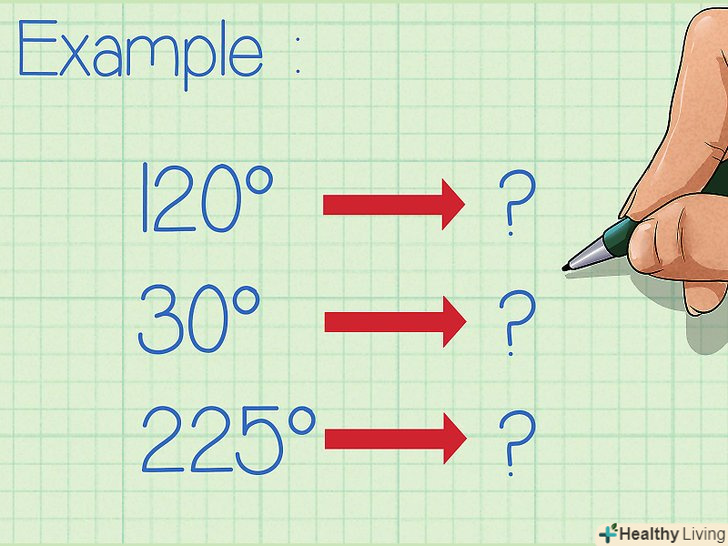
Запишіть градуси, які ви хочете перетворити в радіани.- Приклад 1: 120°
- Приклад 2: 30°
- Приклад 3: 225°
 Помножте градуси на π / 180. пояснення цього множника: так як 180° = π радіан, то 1° = π / 180 радіан. При множенні позбудьтеся від знака градусів, так як відповідь буде записаний в радіанах.
Помножте градуси на π / 180. пояснення цього множника: так як 180° = π радіан, то 1° = π / 180 радіан. При множенні позбудьтеся від знака градусів, так як відповідь буде записаний в радіанах.- Приклад 1: 120 х π/180
- Приклад 2: 30 х π/180
- Приклад 3: 225 х π/180
 Обчисліть радіани.для цього помножте градуси на π і результат запишіть в чисельнику, а в знаменнику залиште 180.
Обчисліть радіани.для цього помножте градуси на π і результат запишіть в чисельнику, а в знаменнику залиште 180.- Приклад 1: 120 х π/180 = 120π / 180
- Приклад 2: 30 х π/180 = 30π / 180
- Приклад 3: 225 х π/180 = 225π / 180
 Спростіть отриманий дріб.для цього розділіть і чисельник, і знаменник на їх найбільший спільний дільник (НСД – найбільше число, на яке діляться і чисельник, і знаменник). У першому прикладі НСД = 60; у другому дорівнює 30; в третьому дорівнює 45. Якщо НСД не виходить знайти швидко, послідовно ділите чисельник і знаменник на 2, 3, 4, 5 або інші відповідні числа. Ось як це робиться:
Спростіть отриманий дріб.для цього розділіть і чисельник, і знаменник на їх найбільший спільний дільник (НСД – найбільше число, на яке діляться і чисельник, і знаменник). У першому прикладі НСД = 60; у другому дорівнює 30; в третьому дорівнює 45. Якщо НСД не виходить знайти швидко, послідовно ділите чисельник і знаменник на 2, 3, 4, 5 або інші відповідні числа. Ось як це робиться:- Приклад 1: 120 х π/180 = 120π/180 ÷ 60/60 = 2π/3 радіан
- Приклад 2: 30 х π/180 = 30π/180 ÷ 30/30 = 1π/6 радіан
- Приклад 3: 225 х π/180 = 225π/180 ÷ 45/45 = 5π / 4 радіан
 Запишіть відповідь.
Запишіть відповідь.- Приклад 1: 120° = 2π/3 радіан
- Приклад 2: 30° = 1π/6 радіан
- Приклад 3: 225° = 5π/4 радіан