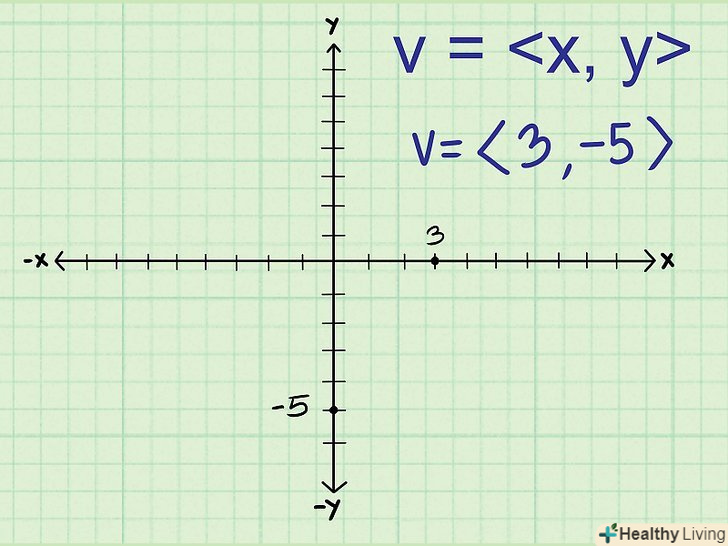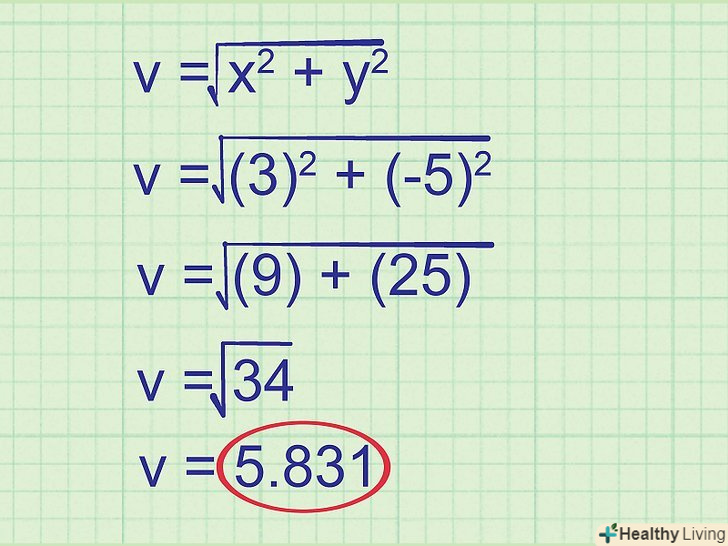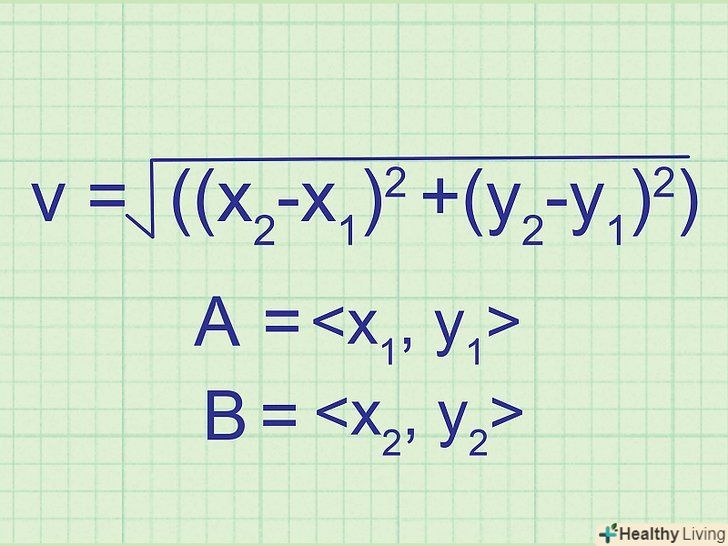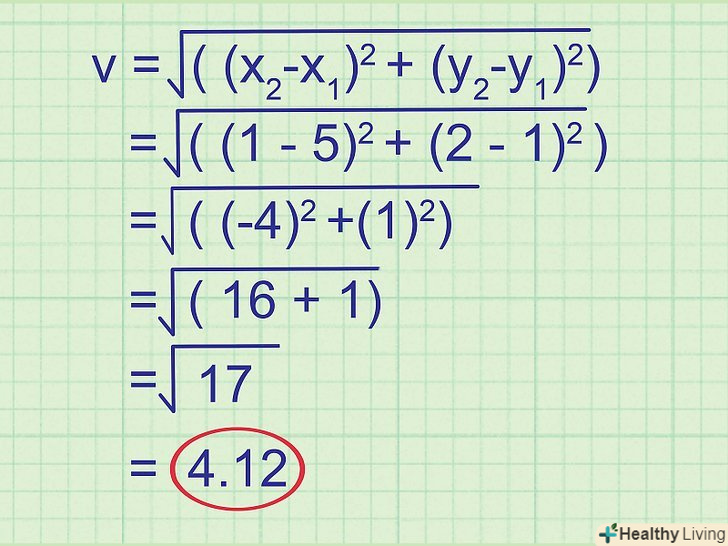ВЕКТОР-це геометричний об'єкт, який характеризується як величиною, так і напрямком.[1] Величина вектора є його довжиною, а напрямок відповідає тому, куди він вказує. Величина вектора обчислюється досить легко, для цього достатньо зробити кілька простих дій. До інших важливих операцій з векторами відносяться додавання і віднімання векторів, знаходження кута між двома векторами і обчислення векторного добутку.
Кроки
Метод1 З 2:
Обчислення величини вектора, що виходить з початку координат
Метод1 З 2:
Визначте компоненти вектора.будь-який вектор на площині можна чисельно представити в двовимірній декартової системі координат двома числами: горизонтальної (вісь X) і вертикальної (вісь Y) компонентою.[2] При цьому вектор записується у вигляді пари чисел:.
- Наприклад, якщо горизонтальна компонента вектора дорівнює 3, а вертикальна становить -5, то цей вектор записується як &#lt;3, -5&#gt;.
-
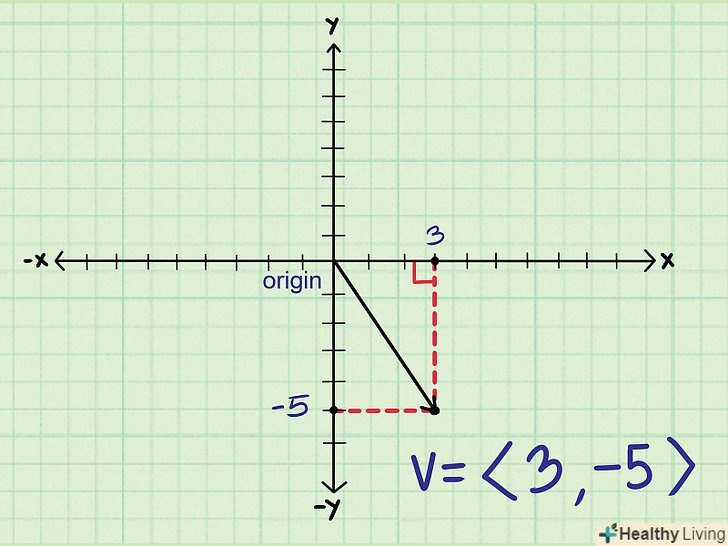
Накресліть векторний трикутник.якщо ви відкладете горизонтальну і вертикальну компоненти, у вас вийде прямокутний трикутник. Величина вектора дорівнює довжині гіпотенузи цього трикутника, і для її обчислення можна скористатися теоремою Піфагора.
-
Щоб обчислити величину вектора, запишіть теорему Піфагора. Теорема Піфагора говорить, що сума квадратів катетів прямокутного трикутника дорівнює квадрату його гіпотенузи: A2 + B2 = C2. У нашому випадку" A "і" B "— це горизонтальна і вертикальна компоненти вектора, а" C " являє собою гіпотенузу. Оскільки гіпотенуза якраз і є вектор, необхідно знайти "C".
- X2 + y2 = v2
- V = √(x2 + y2))
-
Знайдіть величину вектора.для цього підставте в отримане вище рівняння чисельні значення, тобто відповідні компоненти вектора.
- У нашому прикладі v = √((32+(-5)2))
- V =√(9 + 25) = √34 = 5,831
- Нехай вас не бентежить, якщо в результаті вийшло не ціле число. Довжина вектора може бути дробовою величиною.
Метод2 З 2:
Знаходження величини вектора, початок якого не збігається з початком координат
Метод2 З 2:
-
Визначте координати початку і кінця вектора.будь-який вектор на площині можна чисельно представити в двовимірній декартової системі координат двома числами: горизонтальної (вісь X) і вертикальної (вісь Y) компонентою.[3] При цьому вектор записується у вигляді пари чисел:. Якщо початок вектора не збігається з початком декартової системи координат, необхідно визначити координати початкової і кінцевої точки вектора.
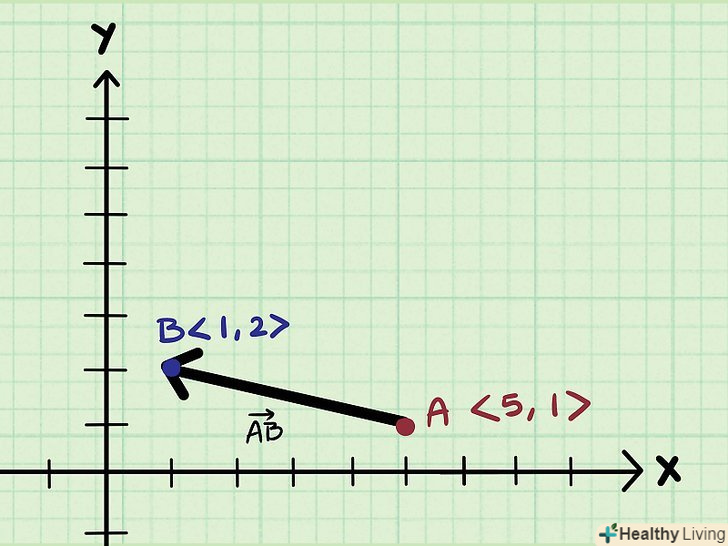
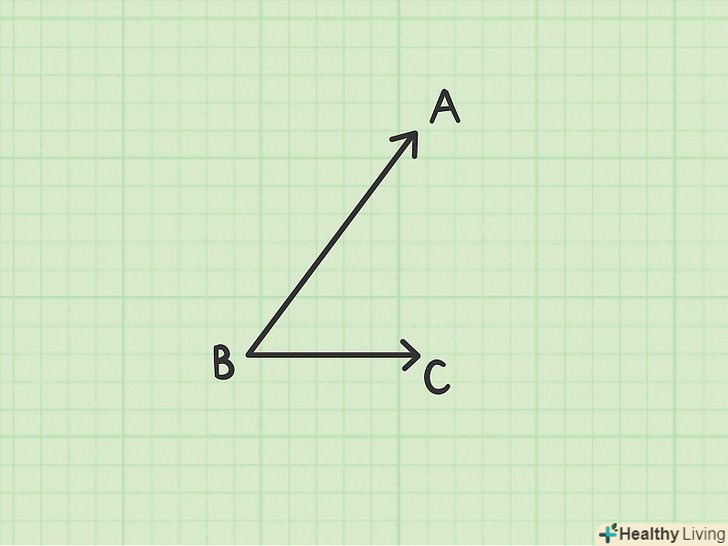
- Нехай вектор AB з'єднує точки A і B.
- Точка A має горизонтальну координату 5 і вертикальну координату 1, тому її координати можна записати у вигляді пари чисел &#lt;5, 1&#gt;.
- Точка B має горизонтальну координату 1 і вертикальну координату 2, тому її координати можна записати у вигляді пари чисел &#lt;1, 2&#gt;.
-
Щоб знайти величину вектора, використовуйте змінену формулу. оскільки в даному випадку задані координати двох точок, слід відняти координати x і y однієї точки з відповідних координат другої точки: v = √((x2-x1)2 +(y2-y1)2).[4]
- Нехай точка A має координати &#lt;x1, y1 &#gt; , а точка B-координати &#Lt; x2, y2 &#gt;
-
Знайдіть величину вектора.підставте координати точок в рівняння і обчисліть довжину вектора. У нашому прикладі обчислення виглядають наступним чином:
- V = √((x2-x1)2 +(y2-y1)2)
- V = √((1-5)2 +(2-1)2)
- V = √((-4)2 +(1)2)
- V = √(16+1) = √(17) = 4,12
- Нехай вас не бентежить, якщо в результаті вийшло не ціле число. Довжина вектора може бути дробовою величиною.
