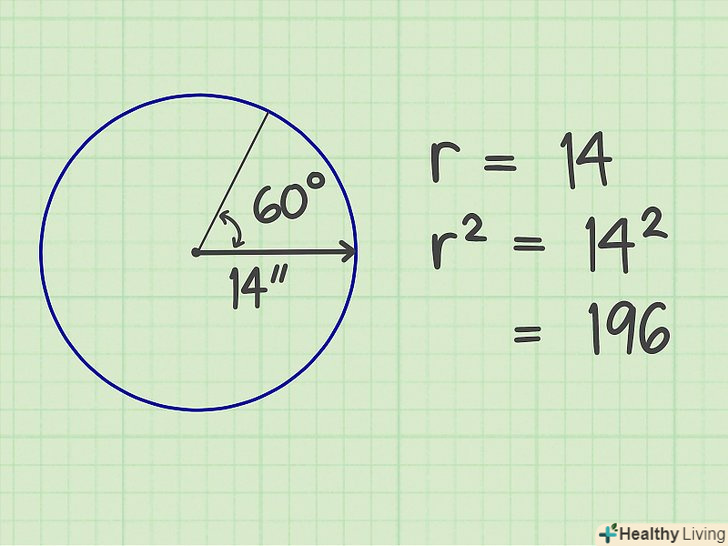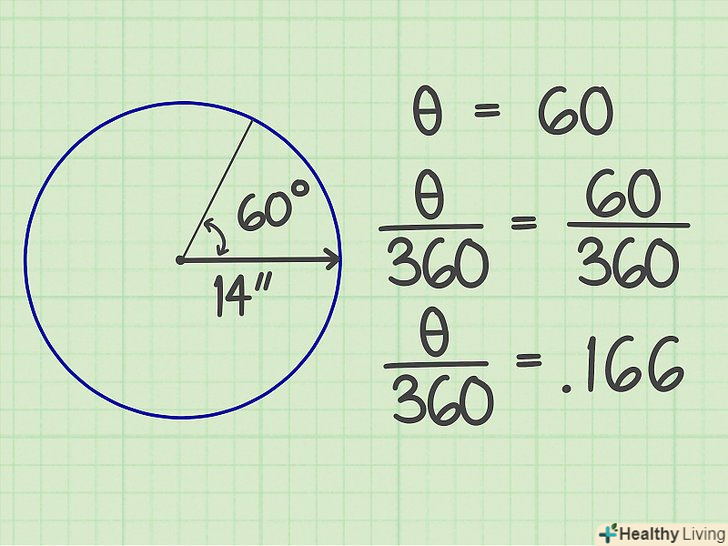Існує безліч різних геометричних фігур і безліч причин для того, щоб знайти їх площа. Прочитайте цю статтю, якщо ви робите домашнє завдання з геометрії або просто хочете з'ясувати кількість фарби для ремонту кімнати.
Кроки
Метод1З 7:
Квадрат, прямокутник, паралелограм
Метод1З 7:
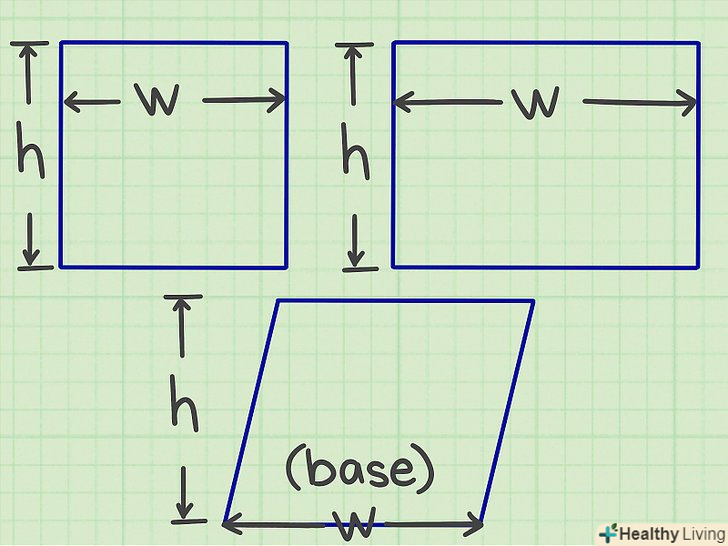
 Виміряйте довжину і ширину фігури.іншими словами, знайдіть значення двох суміжних сторін фігури.[1]
Виміряйте довжину і ширину фігури.іншими словами, знайдіть значення двох суміжних сторін фігури.[1]- У паралелограмі виміряйте висоту і сторону, на яку опущена висота.
- У геометричній задачі значення сторін, як правило, дані. У повсякденному житті сторони необхідно заміряти.
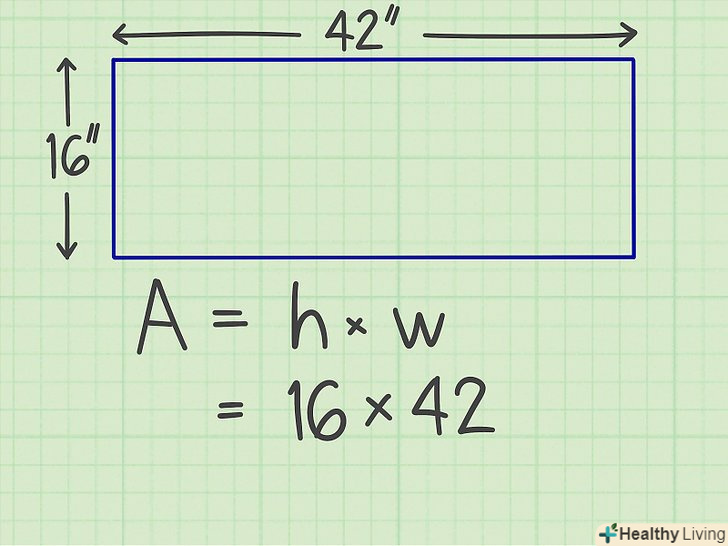
 Перемножте значення сторін, і ви знайдете площу.наприклад, щоб знайти площу прямокутника зі сторонами 16 см і 42 см, потрібно помножити 16 на 42.[2]
Перемножте значення сторін, і ви знайдете площу.наприклад, щоб знайти площу прямокутника зі сторонами 16 см і 42 см, потрібно помножити 16 на 42.[2]- У паралелограмі перемножте висоту і сторону, на яку опущена висота.
- Для обчислення площі квадрата ви можете звести одну з його сторін в квадрат. Для цього можна скористатися калькулятором: для цього спочатку натисніть потрібне число, а потім клавішу, що відповідає за зведення числа в квадрат (на багатьох калькуляторах це x2).
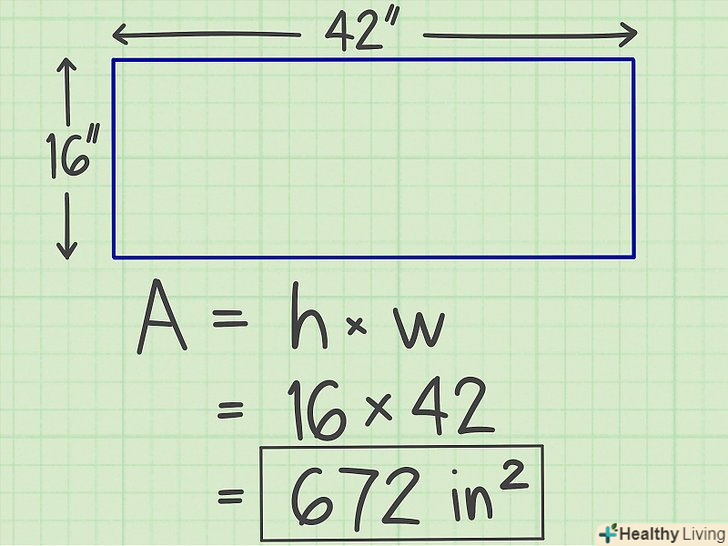
 Запишіть відповідь з одиницями виміру.площа вимірюється в квадратних сантиметрах (метрах, кілометрах і так далі.). Таким чином, площа прямокутника дорівнює 672 квадратних сантиметри.
Запишіть відповідь з одиницями виміру.площа вимірюється в квадратних сантиметрах (метрах, кілометрах і так далі.). Таким чином, площа прямокутника дорівнює 672 квадратних сантиметри.- Нерідко в задачах квадрат числа наводиться так: x2.
Метод2З 7:
Трапеція
Метод2З 7:
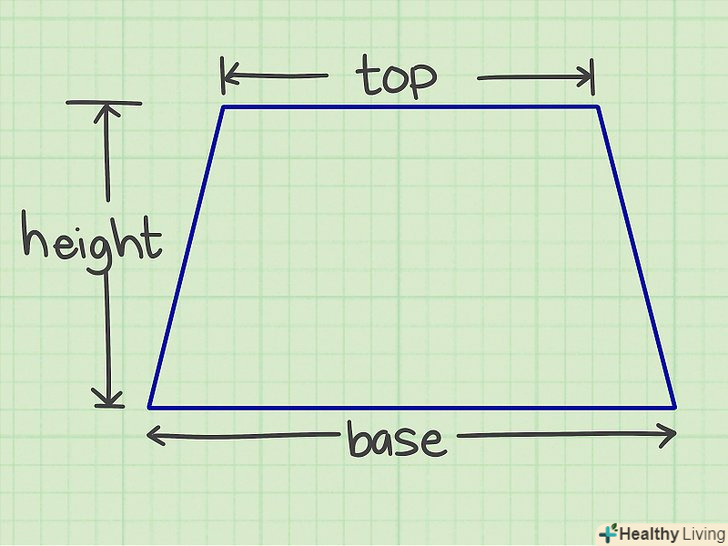
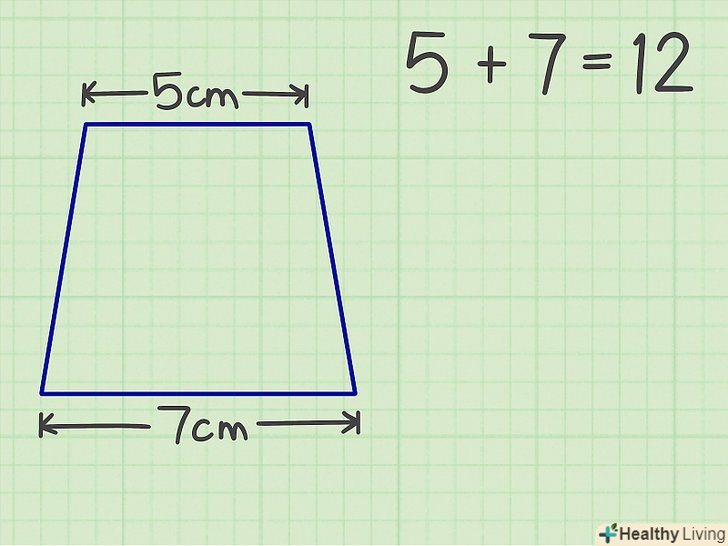
 Знайдіть значення верхнього і нижнього підстав трапеції, а також її висоти.підстави-дві паралельні сторони трапеції; висота — відрізок, розташований перпендикулярно до підстав трапеції.[3]
Знайдіть значення верхнього і нижнього підстав трапеції, а також її висоти.підстави-дві паралельні сторони трапеції; висота — відрізок, розташований перпендикулярно до підстав трапеції.[3]- У геометричній задачі значення сторін, як правило, дані. У повсякденному житті сторони необхідно заміряти.
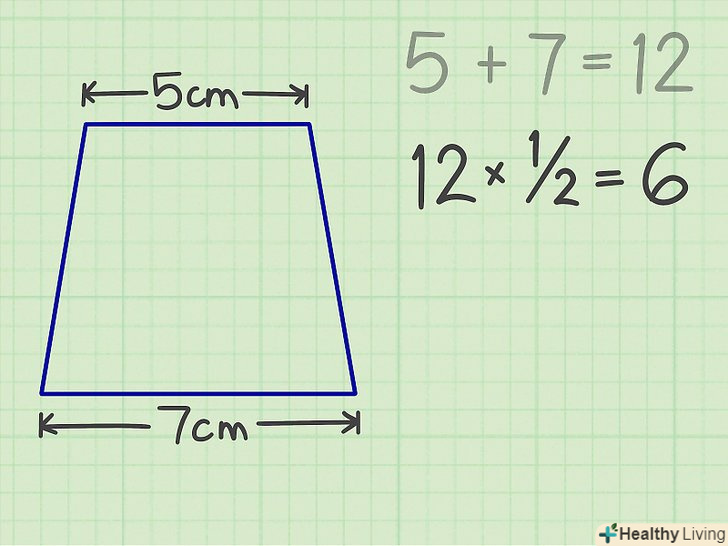
 Складіть верхню і нижню підстави.наприклад, дана трапеція з підставами 5 см і 7 см і висотою 6 см. сума підстав дорівнює 12 см.
Складіть верхню і нижню підстави.наприклад, дана трапеція з підставами 5 см і 7 см і висотою 6 см. сума підстав дорівнює 12 см. Помножте результат на 1/2.у нашому прикладі ви отримаєте 6.
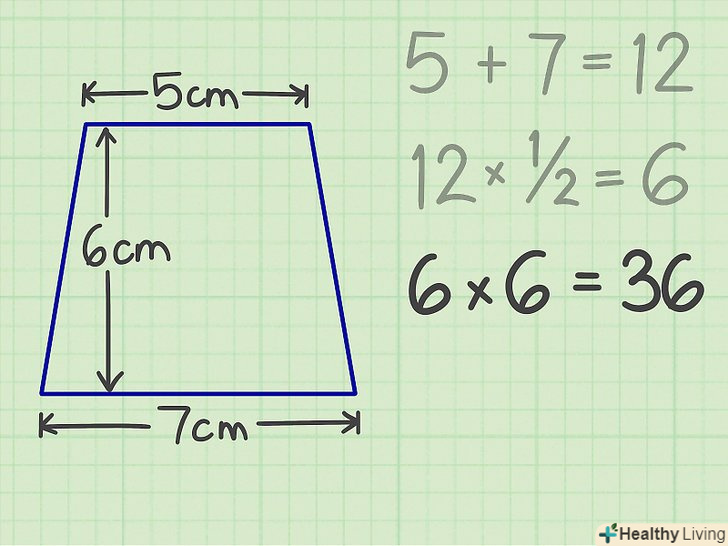
Помножте результат на 1/2.у нашому прикладі ви отримаєте 6. Помножте результат на висоту.у нашому прикладі ви отримаєте 36-це і є площа трапеції.[4]
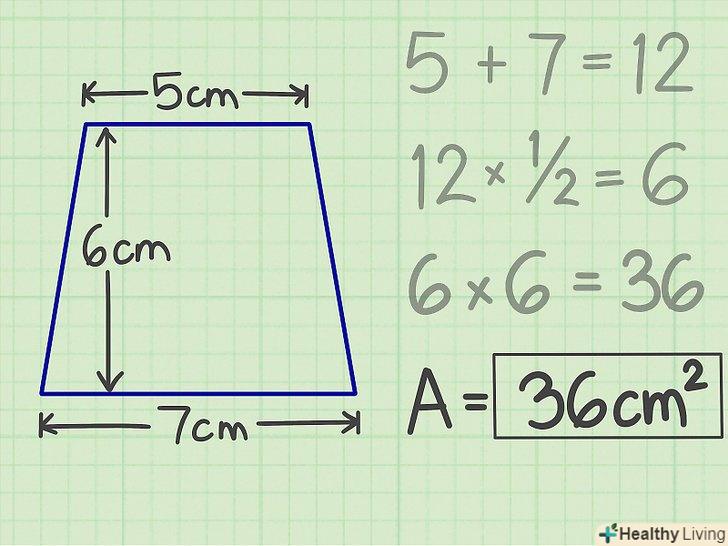
Помножте результат на висоту.у нашому прикладі ви отримаєте 36-це і є площа трапеції.[4] Запишіть відповідь.площа трапеції дорівнює 36 кв. см.
Запишіть відповідь.площа трапеції дорівнює 36 кв. см.
Метод3З 7:
Коло
Метод3З 7:
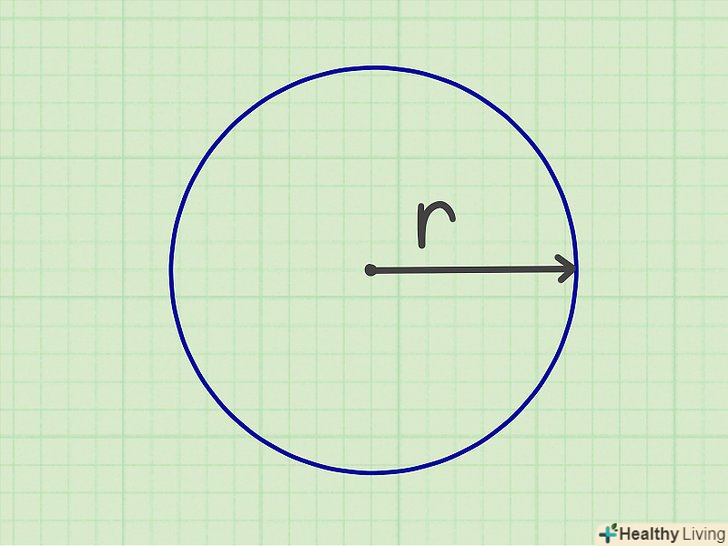
 Знайдіть радіус кола. це відрізок, що з'єднує центр кола і будь-яку точку на окружності. Ви також можете знайти радіус, розділивши діаметр кола навпіл.[5]
Знайдіть радіус кола. це відрізок, що з'єднує центр кола і будь-яку точку на окружності. Ви також можете знайти радіус, розділивши діаметр кола навпіл.[5]- У геометричній задачі значення радіуса або діаметра, як правило, дані. У повсякденному житті їх необхідно заміряти.
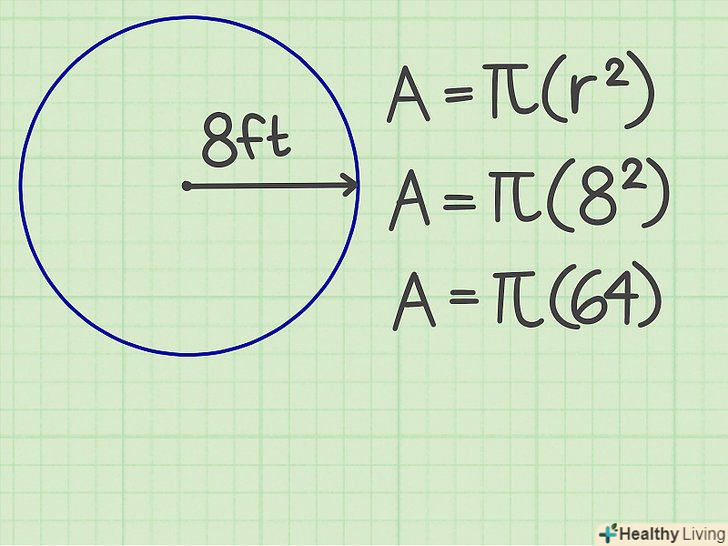
 Зведіть радіус в квадрат (помножте самого на себе).наприклад, радіус дорівнює 8 см. тоді квадрат радіуса дорівнює 64.
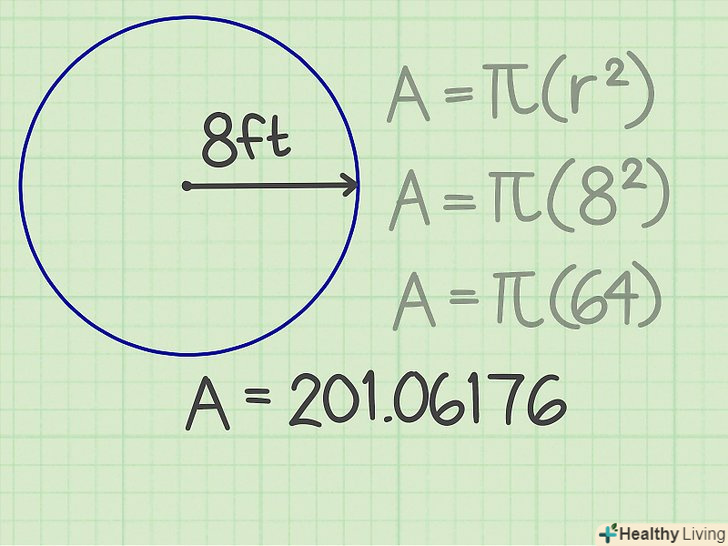
Зведіть радіус в квадрат (помножте самого на себе).наприклад, радіус дорівнює 8 см. тоді квадрат радіуса дорівнює 64. Помножте результат на Пі. Пі (π) – це постійна величина, рівна 3,14159. У нашому прикладі отримаємо 201,06176-це і є площа кола.[6]
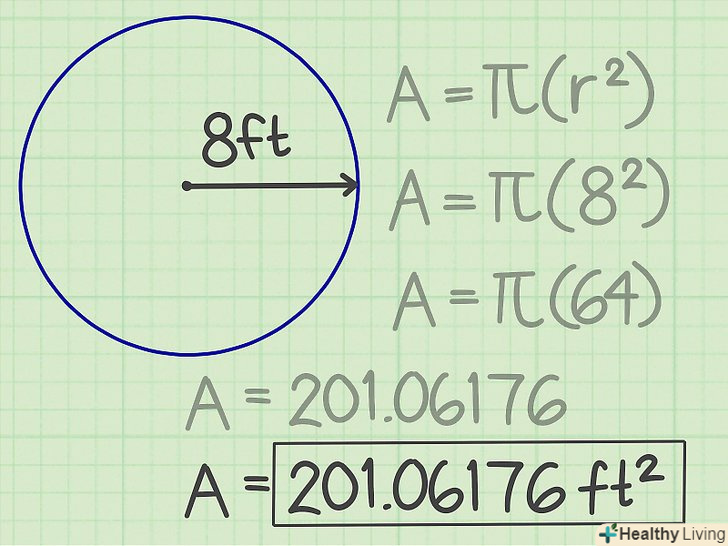
Помножте результат на Пі. Пі (π) – це постійна величина, рівна 3,14159. У нашому прикладі отримаємо 201,06176-це і є площа кола.[6] Запишіть відповідь. площа кола дорівнює 201,06176 кВ. см.
Запишіть відповідь. площа кола дорівнює 201,06176 кВ. см.
Метод4З 7:
Сектор
Метод4З 7:
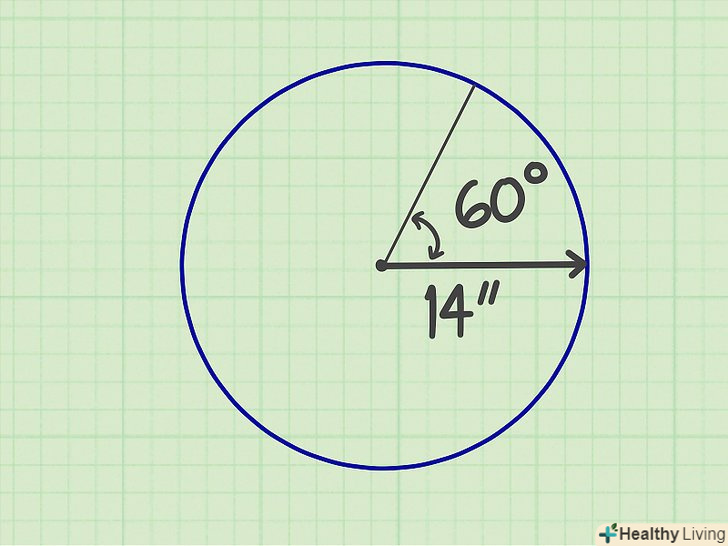
 Використовуйте дані завдання.Сектор-це частина кола, обмежена двома радіусами і дугою. Для обчислення його площі необхідно знати радіус кола і центральний кут. Наприклад: радіус дорівнює 14 см, а кут 60°.[7]
Використовуйте дані завдання.Сектор-це частина кола, обмежена двома радіусами і дугою. Для обчислення його площі необхідно знати радіус кола і центральний кут. Наприклад: радіус дорівнює 14 см, а кут 60°.[7]- У геометричній задачі початкові Дані, як правило, дані. У повсякденному житті їх необхідно заміряти.
 Зведіть радіус в квадрат (помножте самого на себе).у нашому прикладі квадрат радіуса дорівнює 196 (14x14).
Зведіть радіус в квадрат (помножте самого на себе).у нашому прикладі квадрат радіуса дорівнює 196 (14x14). Помножте результат на Пі. Пі (π) — це постійна величина, рівна 3,14159. У нашому прикладі отримаємо 615,75164.[8]
Помножте результат на Пі. Пі (π) — це постійна величина, рівна 3,14159. У нашому прикладі отримаємо 615,75164.[8] Розділіть центральний кут на 360.у нашому прикладі центральний кут дорівнює 60 градусам, в результаті отримаємо 0,166.
Розділіть центральний кут на 360.у нашому прикладі центральний кут дорівнює 60 градусам, в результаті отримаємо 0,166. Помножте цей результат (поділ кута на 360 ) на результат, отриманий раніше (добуток Пі на квадрат радіуса).у нашому прикладі ви отримаєте 102,214-це і є Площа сектора.
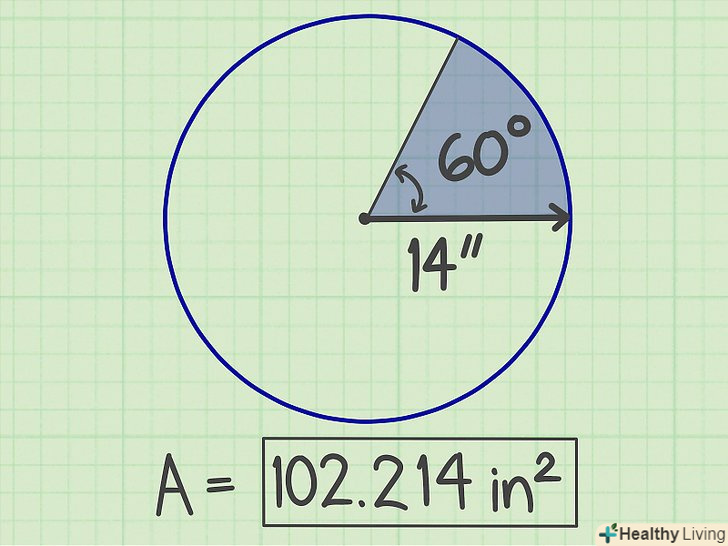
Помножте цей результат (поділ кута на 360 ) на результат, отриманий раніше (добуток Пі на квадрат радіуса).у нашому прикладі ви отримаєте 102,214-це і є Площа сектора. Запишіть відповідь.площа сектора дорівнює 102,214 кВ. см.
Запишіть відповідь.площа сектора дорівнює 102,214 кВ. см.
Метод5З 7:
Еліпс
Метод5З 7:
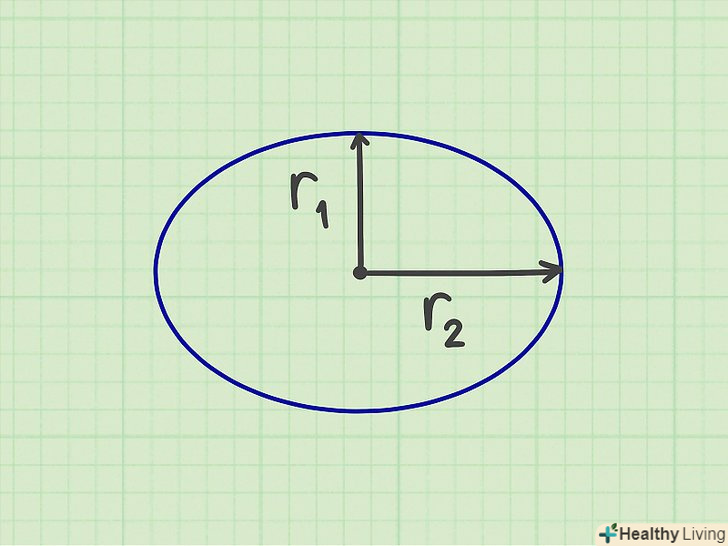
 Використовуйте початкові Дані.для обчислення площі еліпса потрібно знати велику піввісь і малу піввісь еліпса (тобто половини осей еліпса). Півосі - це відрізки, проведені з центру еліпса до його вершин на великій і малій осях. Півосі утворюють прямий кут.[9]
Використовуйте початкові Дані.для обчислення площі еліпса потрібно знати велику піввісь і малу піввісь еліпса (тобто половини осей еліпса). Півосі - це відрізки, проведені з центру еліпса до його вершин на великій і малій осях. Півосі утворюють прямий кут.[9]- У геометричній задачі початкові Дані, як правило, дані. У повсякденному житті їх необхідно заміряти.
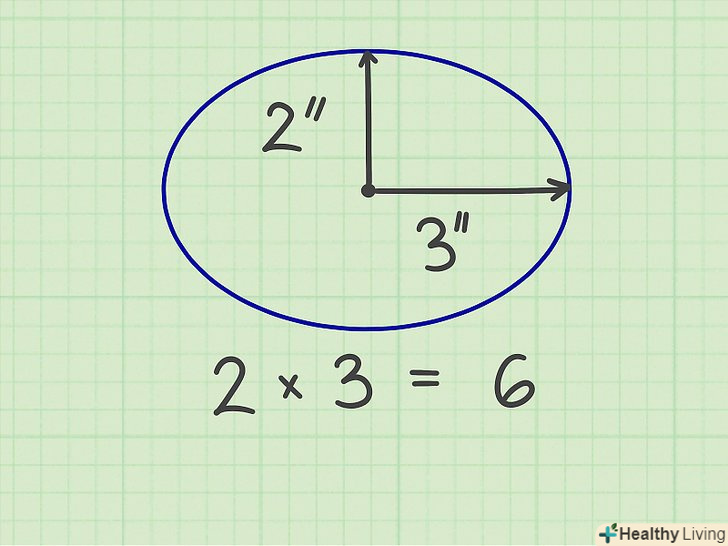
 Перемножте Півосі.наприклад, осі еліпса рівні 6 см і 4 см.Таким чином, Півосі еліпса рівні 3 см і 2 см. перемножте Півосі і отримаєте 6.
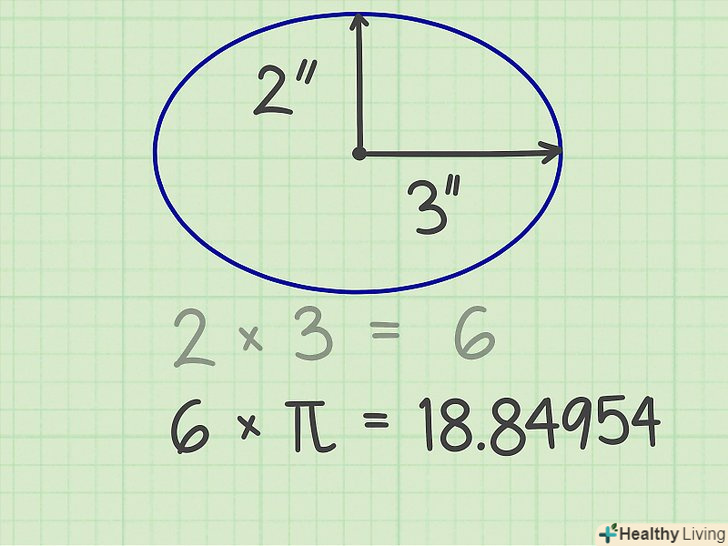
Перемножте Півосі.наприклад, осі еліпса рівні 6 см і 4 см.Таким чином, Півосі еліпса рівні 3 см і 2 см. перемножте Півосі і отримаєте 6. Помножте результат на пі. Пі (π) — це постійна величина, рівна 3,14159. У нашому прикладі отримаємо 18,84954-це і є Площа еліпса.
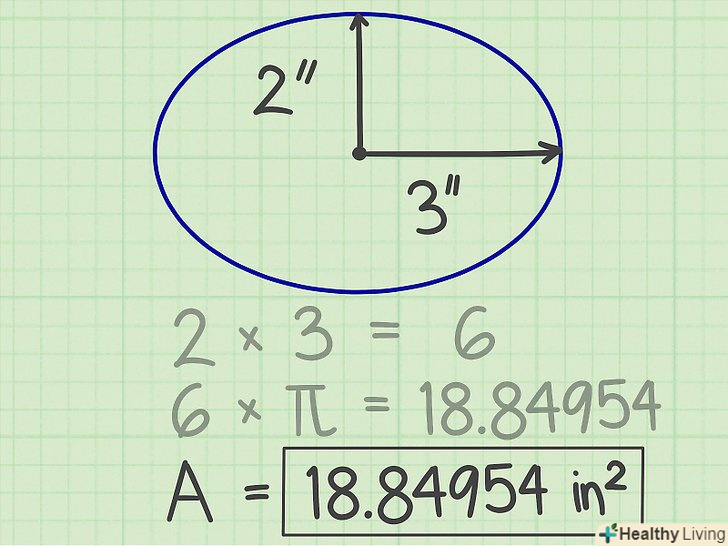
Помножте результат на пі. Пі (π) — це постійна величина, рівна 3,14159. У нашому прикладі отримаємо 18,84954-це і є Площа еліпса. Запишіть відповідь. Площа еліпса дорівнює 18,84954 кВ. см.
Запишіть відповідь. Площа еліпса дорівнює 18,84954 кВ. см.
Метод6З 7:
Трикутник
Метод6З 7:
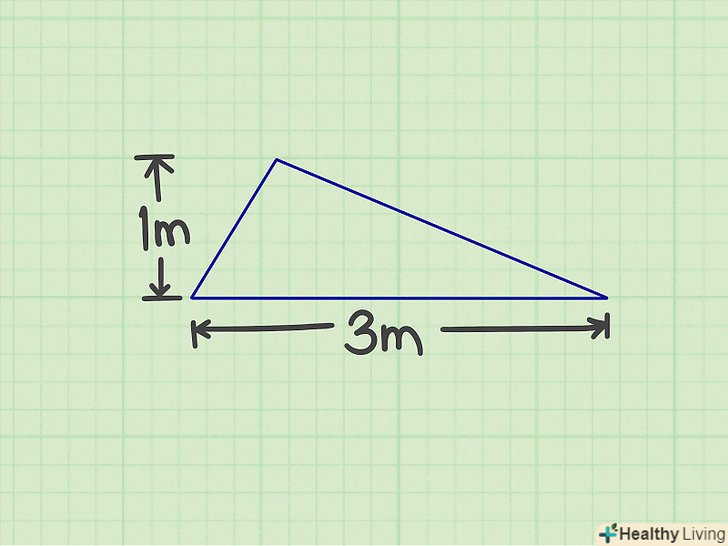
 Знайдіть значення висоти трикутника і сторони, на яку опущена ця висота. наприклад, висота трикутника дорівнює 1 м, а сторона, на яку опущена висота, дорівнює 3 м.[10]
Знайдіть значення висоти трикутника і сторони, на яку опущена ця висота. наприклад, висота трикутника дорівнює 1 м, а сторона, на яку опущена висота, дорівнює 3 м.[10]- У геометричній задачі початкові Дані, як правило, дані. У повсякденному житті їх необхідно заміряти.
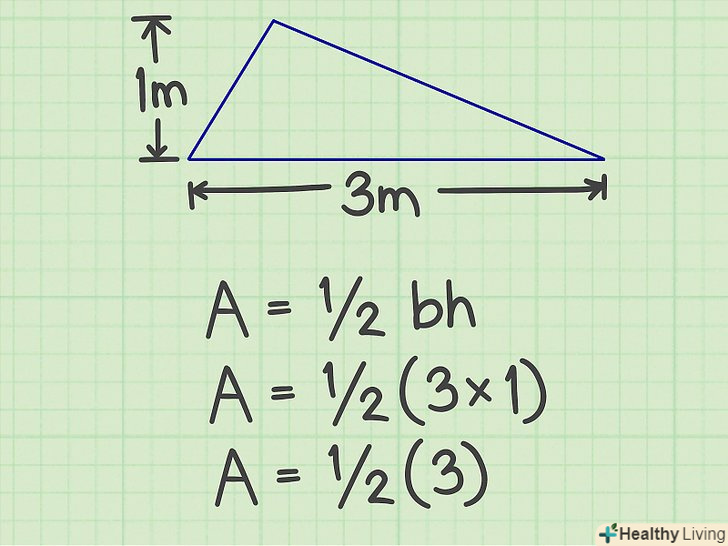
 Перемножте висоту і сторону.у нашому прикладі ви отримаєте 3.[11]
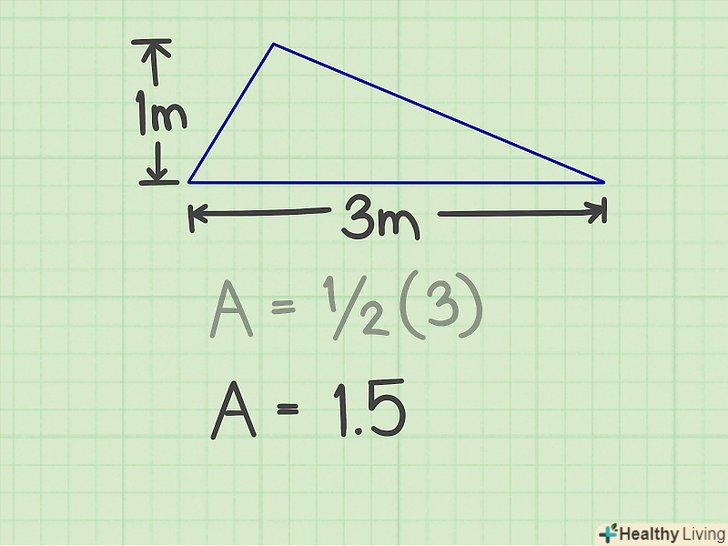
Перемножте висоту і сторону.у нашому прикладі ви отримаєте 3.[11] Помножте результат на 1/2.у нашому прикладі ви отримаєте 1,5-це і є площа трикутника.
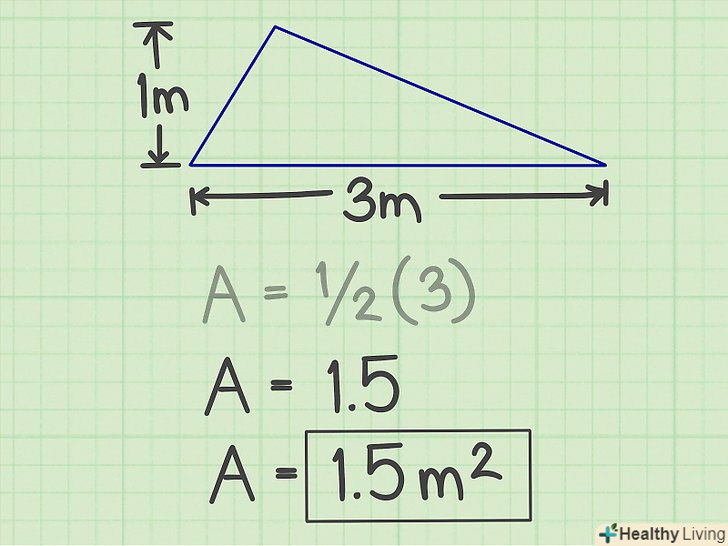
Помножте результат на 1/2.у нашому прикладі ви отримаєте 1,5-це і є площа трикутника. Запишіть відповідь.площа трикутника дорівнює 1,5 кв. м.
Запишіть відповідь.площа трикутника дорівнює 1,5 кв. м.
Метод7З 7:
Фігури складної форми
Метод7З 7:
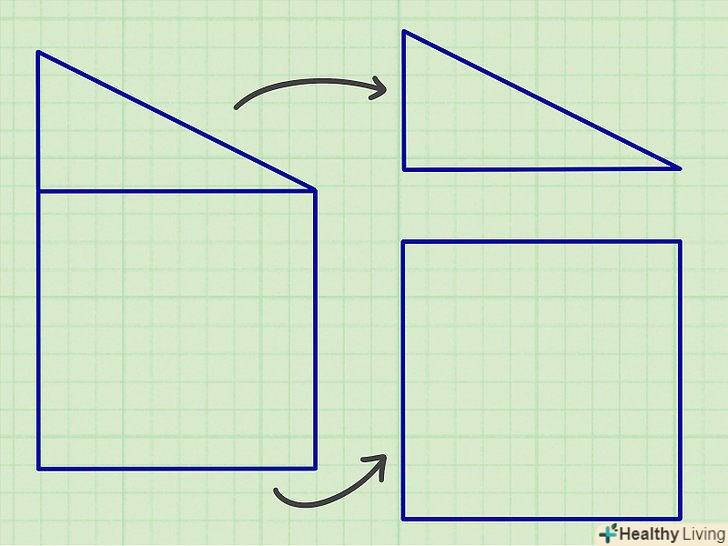
 Для обчислення площі фігури складної форми розбийте її на кілька стандартних фігур, обчисліть площу кожної з них і складіть результати.у геометричній задачі це легко зробити, але в повсякденному житті вам, швидше за все, доведеться розбити фігуру складної форми на безліч стандартних фігур.[12]
Для обчислення площі фігури складної форми розбийте її на кілька стандартних фігур, обчисліть площу кожної з них і складіть результати.у геометричній задачі це легко зробити, але в повсякденному житті вам, швидше за все, доведеться розбити фігуру складної форми на безліч стандартних фігур.[12]- Почніть з пошуку прямих кутів і паралельних ліній. Вони послужать в якості основ для стандартних фігур.
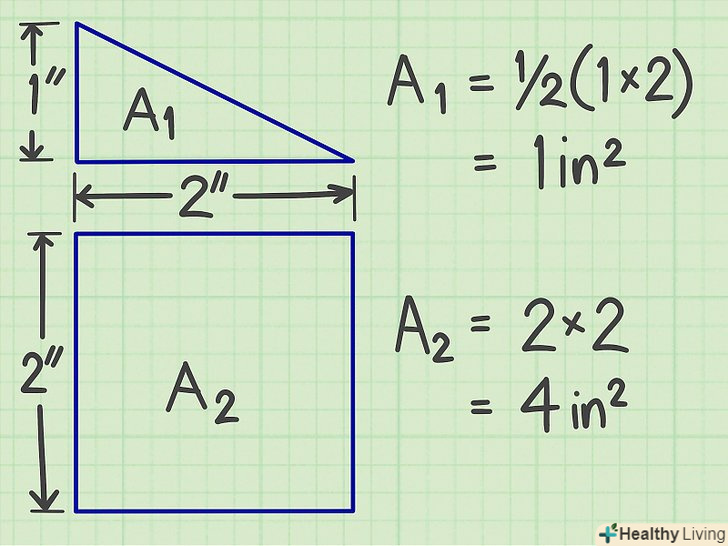
 Обчислити площу кожної стандартної фігури, застосувавши вищеописані методи.
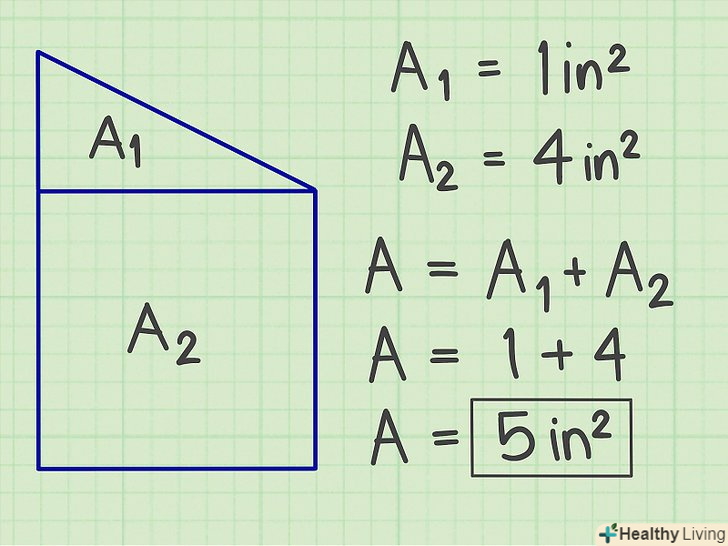
Обчислити площу кожної стандартної фігури, застосувавши вищеописані методи. Складіть знайдені площі.так ви обчислите площу фігури складної форми.
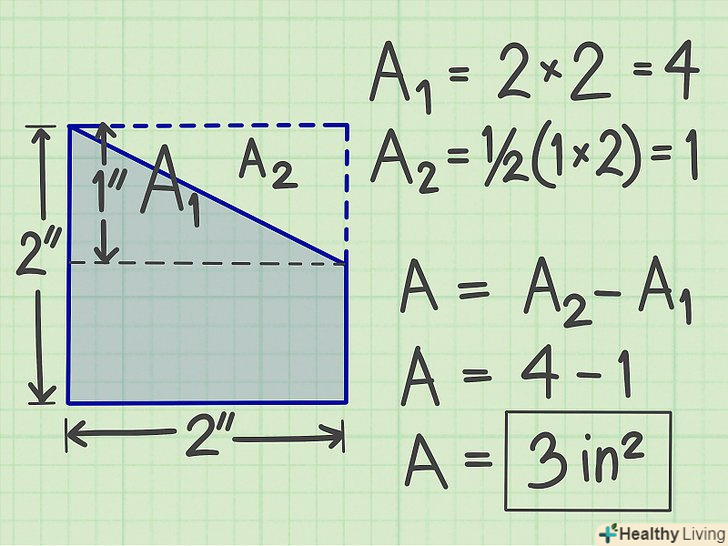
Складіть знайдені площі.так ви обчислите площу фігури складної форми. Використовуйте альтернативні методи.наприклад, до фігури складної форми прірісуйте "уявну" фігуру, яка перетворить фігуру складної форми в стандартну фігуру. Знайдіть площу такої стандартної фігури, а потім відніміть з неї площу «уявної» фігури. Ви знайдете площу фігури складної форми.
Використовуйте альтернативні методи.наприклад, до фігури складної форми прірісуйте "уявну" фігуру, яка перетворить фігуру складної форми в стандартну фігуру. Знайдіть площу такої стандартної фігури, а потім відніміть з неї площу «уявної» фігури. Ви знайдете площу фігури складної форми.
Поради
- скористайтеся цим калькулятором площ, якщо вам потрібна допомога або ви хочете подивитися на процес обчислень.
- Якщо вам потрібна допомога, попросіть її у людини, що розбирається в геометрії.
Попередження
- Переконайтеся, що в обчисленнях беруть участь величини, виміряні в одних одиницях (наприклад, тільки в сантиметрах, або тільки в метрах і так далі).
- Завжди перевіряйте відповідь!
Джерела
- ↑ Https://www.mathsisfun.com/geometry/rectangle.html
- ↑ Https://www.mathsisfun.com/geometry/square.html
- ↑ Https://www.khanacademy.org/math/basic-geo/basic-geo-area-and-perimeter/area-trap-composite/v/area-of-a-trapezoid-1
- ↑ Https://www.mathgoodies.com/lessons/vol1/area_trapezoid
- ↑ Https://www.khanacademy.org/math/basic-geo/basic-geo-area-and-perimeter/area-circumference-circle/v/area-of-a-circle
- ↑ Https://www.mathsisfun.com/geometry/circle-area-by-sectors.html
- ↑ Https://www.khanacademy.org/math/geometry/hs-geo-circles/hs-geo-sectors/v/area-of-a-sector-given-a-central-angle
- ↑ Https://www.mathopenref.com/arcsectorarea.html
- ↑ Https://www.math.hmc.edu/funfacts/ffiles/10006.3.shtml
- ↑ Https://www.khanacademy.org/math/basic-geo/basic-geo-area-and-perimeter/area-triangle/a/area-of-triangle
- ↑ Https://www.khanacademy.org/math/basic-geo/basic-geo-area-and-perimeter/area-triangle/v/example-finding-area-of-triangle
- ↑ Https://www.khanacademy.org/math/basic-geo/basic-geo-area-and-perimeter/area-trap-composite/v/area-breaking-up-shape
- Https://www.mathsisfun.com/area.html