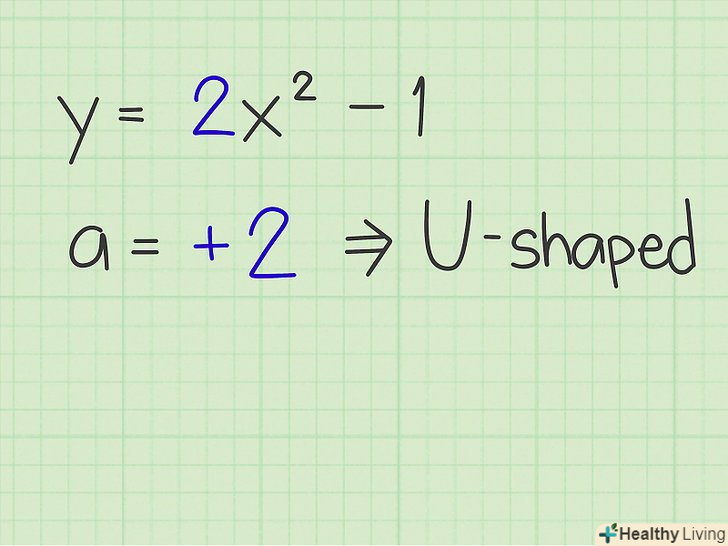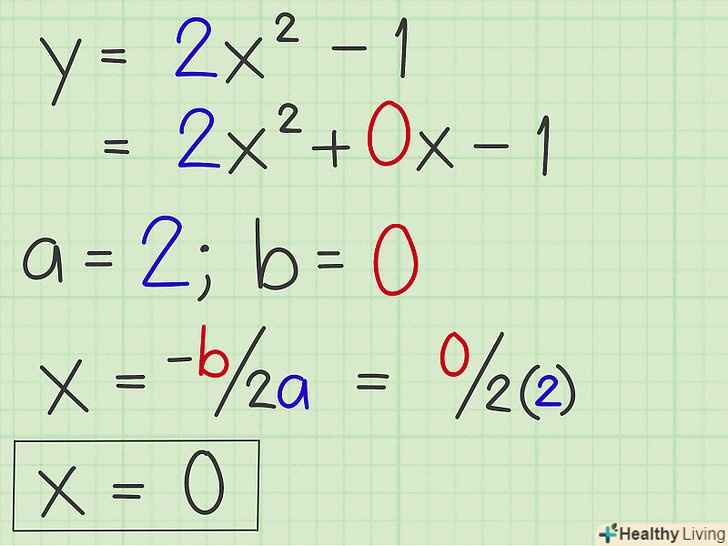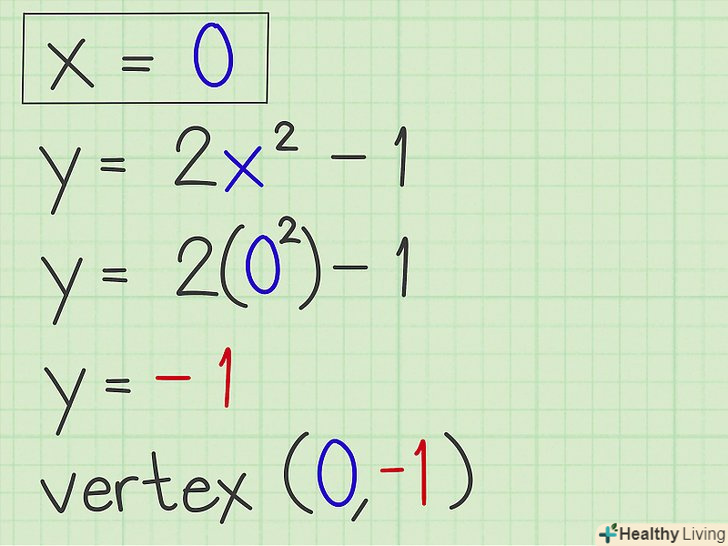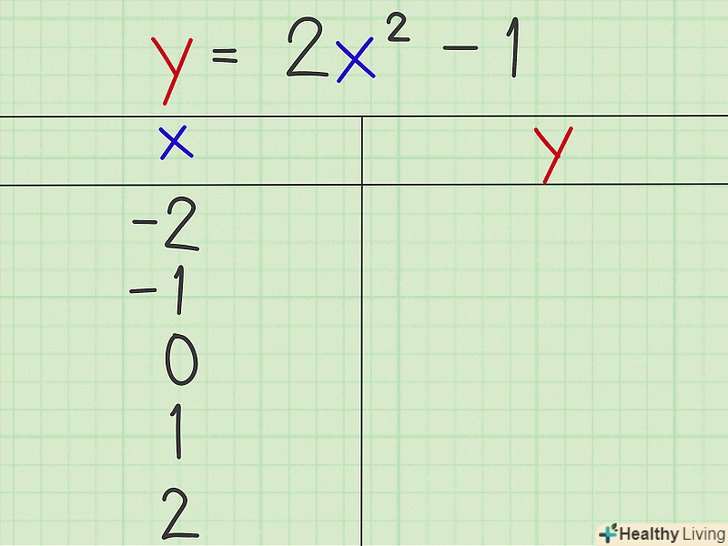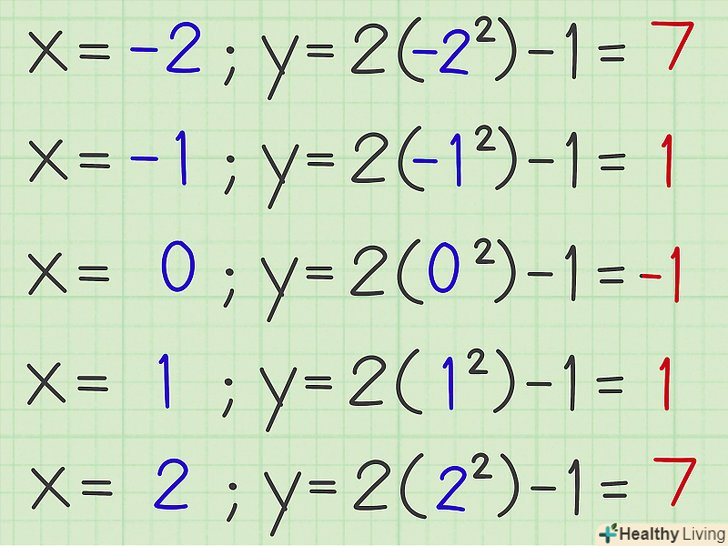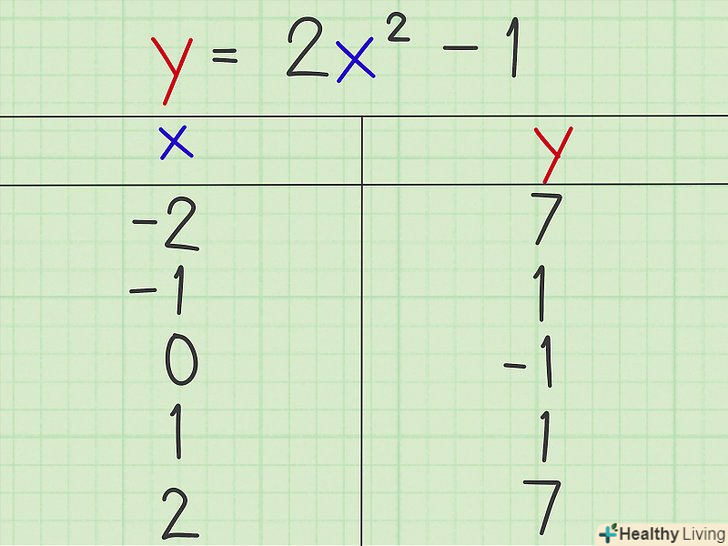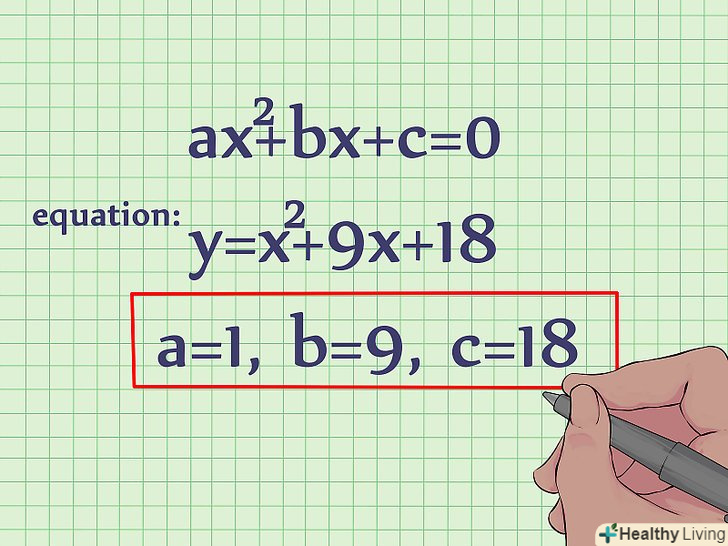Парабола являє собою геометричне місце точок, рівновіддалених від даної прямої (директриси) і даної точки (фокуса). Це двовимірна, дзеркально-симетрична крива. Для побудови параболи необхідно знайти її вершину і кілька точок по обидва боки від вершини.
Кроки
Частина1 З 2:
Побудова параболи
Частина1 З 2:
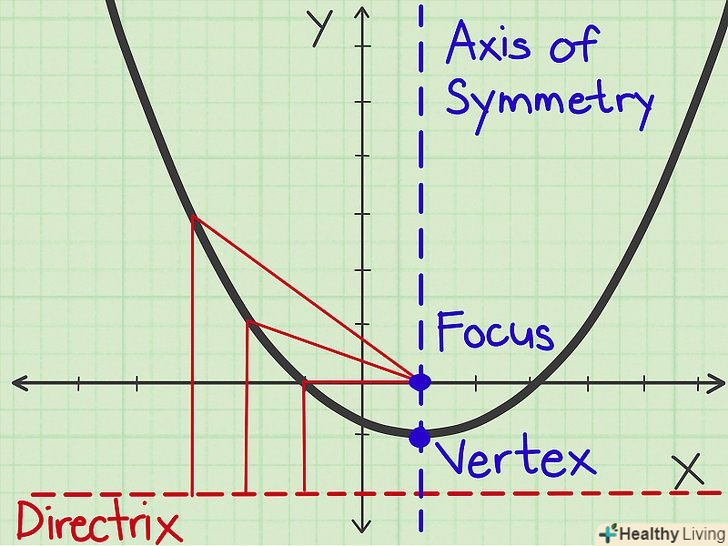
 Термінологія.знання термінології допоможе вам при побудові параболи.[1]
Термінологія.знання термінології допоможе вам при побудові параболи.[1]- Фокус параболи - це точка, від якої рівновіддалені всі точки, що лежать на параболі.
- Директриса параболи - це пряма, від якої рівновіддалені всі точки, що лежать на параболі.
- вісь симетрії параболи - це вертикальна лінія, що проходить через фокус і вершину параболи перпендикулярно її директрисі.
- Вершина параболи - точка перетину параболи і осі симетрії. Якщо парабола спрямована вгору, то вершина є найнижчою точкою параболи; якщо парабола спрямована вниз, то вершина є найвищою точкою параболи.
 Рівняння параболи.рівняння параболи має вигляд: y=ax2+bx+c. Рівняння параболи також можна записати у вигляді y = a (x – h)2 + k.
Рівняння параболи.рівняння параболи має вигляд: y=ax2+bx+c. Рівняння параболи також можна записати у вигляді y = a (x – h)2 + k.- Якщо коефіцієнт «а «позитивний, то парабола спрямована вгору, а якщо коефіцієнт» а " негативний, то парабола спрямована вниз. Для запам'ятовування цього правила: при позитивному (позитивному) коефіцієнті парабола «посміхається» (спрямована вгору) і навпаки при негативному (негативному) коефіцієнті.
- Наприклад:y = 2x 2-1. Парабола цього рівняння спрямована вгору, так як а = 2 (позитивний коефіцієнт).
- Якщо в рівнянні в квадрат зводиться «у«, а не» х«, то парабола» лежить на боці " і спрямована вправо або вліво. Наприклад, парабола y2 = x + 3 спрямована вправо.
 Знайдіть вісь симетрії.вісь симетрії параболи-це вертикальна лінія, що проходить через вершину параболи. Вісь симетрії задається функцією х = n, де n-координата " х " вершини параболи. Для обчислення осі симетрії скористайтеся формулою x = - b/2a.[2]
Знайдіть вісь симетрії.вісь симетрії параболи-це вертикальна лінія, що проходить через вершину параболи. Вісь симетрії задається функцією х = n, де n-координата " х " вершини параболи. Для обчислення осі симетрії скористайтеся формулою x = - b/2a.[2]- У нашому прикладі а = 2, b = 0. Підставте ці значення в формулу: х = -0/(2 х 2) = 0.
- Вісь симетрії х = 0.
 Знайдіть вершину.обчисливши вісь симетрії, Ви знайшли координату " х " вершини параболи. Підставте знайдене значення в початкове рівняння, щоб знайти «у». Ці дві координати і є координати вершини параболи. У нашому прикладі підставте х = 0 в у = 2x2 -1 і отримаєте у = -1. Вершина параболи має координати (0, -1). Більш того, це точка перетину параболи з віссю Y (так як х = 0).[3]
Знайдіть вершину.обчисливши вісь симетрії, Ви знайшли координату " х " вершини параболи. Підставте знайдене значення в початкове рівняння, щоб знайти «у». Ці дві координати і є координати вершини параболи. У нашому прикладі підставте х = 0 в у = 2x2 -1 і отримаєте у = -1. Вершина параболи має координати (0, -1). Більш того, це точка перетину параболи з віссю Y (так як х = 0).[3]- Іноді координати вершини позначаються як (h,k). У нашому прикладі h = 0, k = -1. Якщо квадратне рівняння дано у виглядіy = a (x – h)2 + k, то можна з легкістю знайти координати вершини безпосередньо з рівняння (без обчислень).
 Намалюйте таблицю з двома стовпцями. у першому стовпці будуть розташовані значення "х«, а в другому — значення»у". Це будуть координати точок, що лежать на параболі.
Намалюйте таблицю з двома стовпцями. у першому стовпці будуть розташовані значення "х«, а в другому — значення»у". Це будуть координати точок, що лежать на параболі.- «середнім "значенням" х "виберіть координату" х " вершини параболи.
- Вище і нижче «середнього "значення" х «напишіть по два значення» х " (для симетрії).
- У нашому прикладі запишіть х = 0 в середині таблиці.
 Обчисліть значення "у".для цього підставте значення "х «з таблиці в дане вам рівняння, а потім запишіть отримані значення» у" в таблицю.
Обчисліть значення "у".для цього підставте значення "х «з таблиці в дане вам рівняння, а потім запишіть отримані значення» у" в таблицю.- x = -2, y = 2 x (-2)2 - 1 = 8 - 1 = 7
- x = -1, y = 2 x (-1)2 - 1 = 2 - 1 = 1
- x = 0, y = 2 x (0)2 - 1 = 0 - 1 = -1
- x = 1, y = 2 x (1)2 - 1 = 2 - 1 = 1
- x = 2, y = 2 x (2)2 - 1 = 8 - 1 = 7
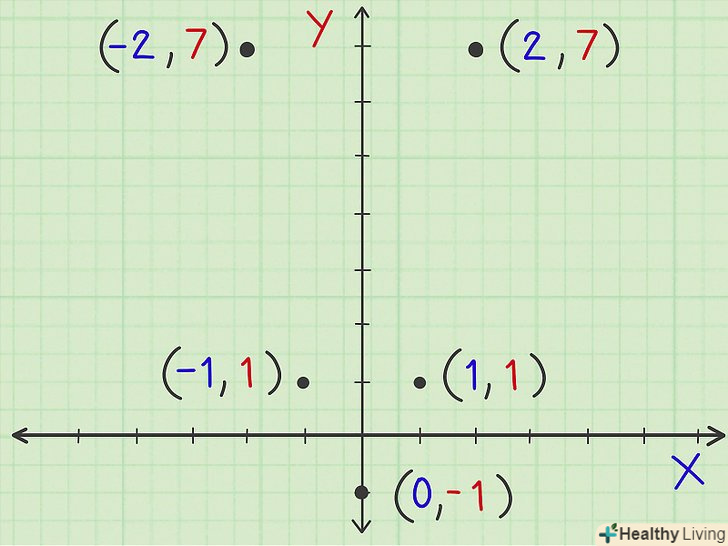
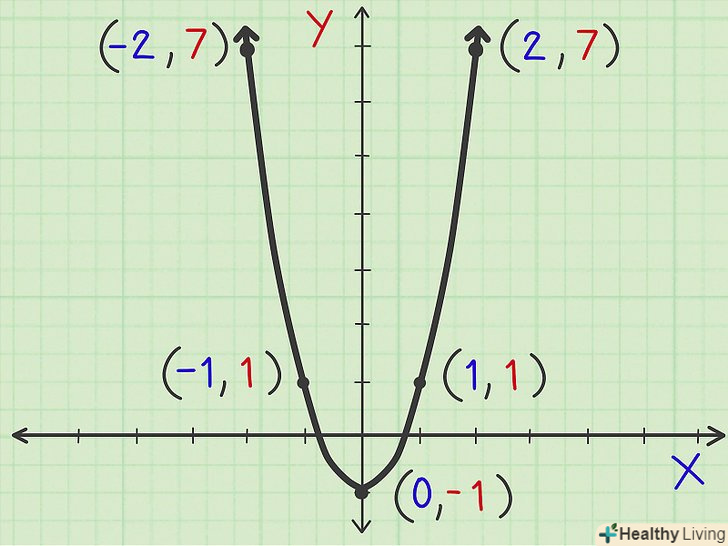
 Тепер, коли Ви знайшли координати п'яти точок, ви можете побудувати графік. Ви знайшли п'ять точок з координатами (-2,7), (-1,1), (0,-1), (1,1), (2,7). Зверніть увагу, що при симетричних (щодо осі симетрії) значеннях «х» значення «у» збігаються, тобто, наприклад, при х = -2 і х = 2 у = 7.
Тепер, коли Ви знайшли координати п'яти точок, ви можете побудувати графік. Ви знайшли п'ять точок з координатами (-2,7), (-1,1), (0,-1), (1,1), (2,7). Зверніть увагу, що при симетричних (щодо осі симетрії) значеннях «х» значення «у» збігаються, тобто, наприклад, при х = -2 і х = 2 у = 7. Нанесіть знайдені точки на координатній площині. кожен рядок таблиці-це координати (х,у) однієї точки.
Нанесіть знайдені точки на координатній площині. кожен рядок таблиці-це координати (х,у) однієї точки.- Вісь Х йде вліво і вправо; вісь Y йде вгору і вниз.
- Позитивні значення по осі Y відкладаються вгору від точки (0,0), а негативні — вниз від точки (0,0).
- Позитивні значення по осі Х відкладаються вправо від точки (0,0), а негативні — вліво від точки (0,0).
 З'єднайте точки U-подібної кривої, і ви отримаєте параболу.З'єднуйте точки плавною кривою, а не ламаною лінією, щоб отримати правильну параболу. За бажанням можете намалювати стрілки на кінцях параболи, спрямовані в сторону від вершини. Це послужить ознакою того, що парабола нескінченна.[4]
З'єднайте точки U-подібної кривої, і ви отримаєте параболу.З'єднуйте точки плавною кривою, а не ламаною лінією, щоб отримати правильну параболу. За бажанням можете намалювати стрілки на кінцях параболи, спрямовані в сторону від вершини. Це послужить ознакою того, що парабола нескінченна.[4]
Частина2 З 2:
Зсув параболи
Частина2 З 2:
Якщо ви хочете зрушити параболу на координатній площині без обчислення її вершини і додаткових точок, то вам потрібно навчитися «читати» рівняння параболи. Почніть з найпростішого рівняння параболи:у = x2. Її вершина має координати (0,0), а сама парабола спрямована вгору. Точки, що лежать на цій параболі, мають координати (-1,1), (1,1), (2,4), (2,4) (і так далі). Тепер ми покажемо вам, як зрушити цю параболу.[5]
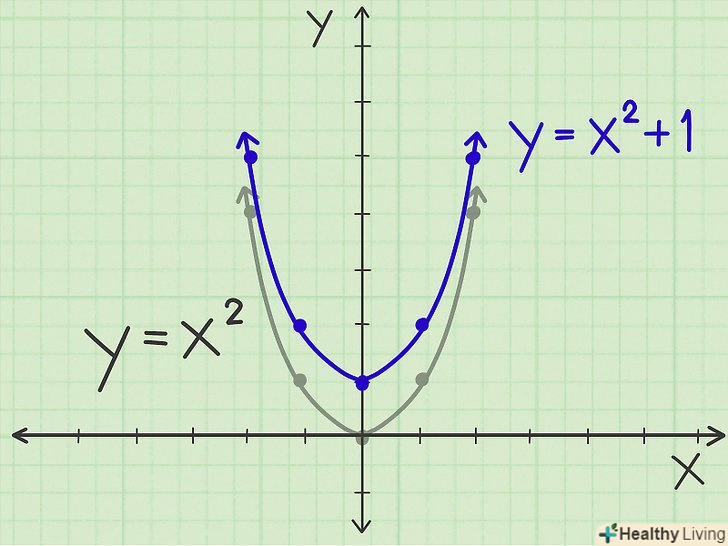
 Зсув вгору.перепишіть рівняння так: y = x2 +1, тобто парабола зрушиться вгору на 1 одиницю (вершина нової параболи має координати (0, 1)). Нова парабола матиме таку ж форму, як і вихідна, але координата «у» кожної точки збільшиться на 1 одиницю. Таким чином, замість точок (-1, 1) і (1, 1) Ви отримаєте точки (-1, 2) і (1, 2) (і так далі).
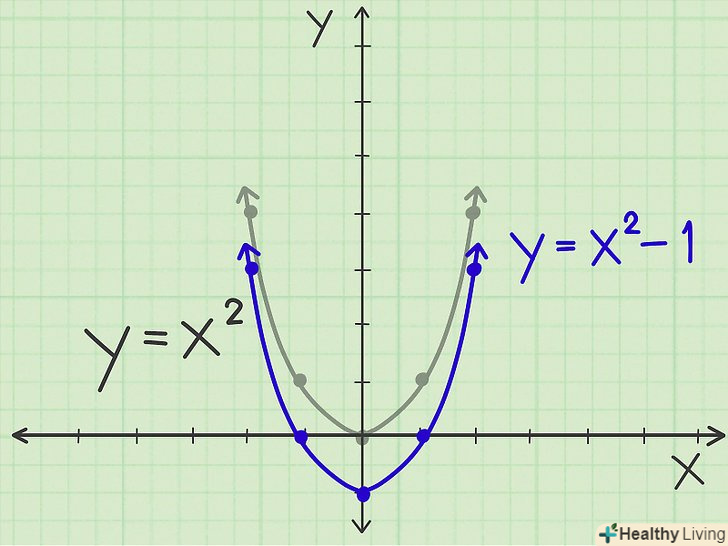
Зсув вгору.перепишіть рівняння так: y = x2 +1, тобто парабола зрушиться вгору на 1 одиницю (вершина нової параболи має координати (0, 1)). Нова парабола матиме таку ж форму, як і вихідна, але координата «у» кожної точки збільшиться на 1 одиницю. Таким чином, замість точок (-1, 1) і (1, 1) Ви отримаєте точки (-1, 2) і (1, 2) (і так далі). Зсув вниз. перепишіть рівняння так:y = x2 -1 , тобто парабола зрушиться вниз на 1 одиницю (вершина нової параболи має координати (0, -1)). Нова парабола матиме таку ж форму, як і вихідна, але координата «у» кожної точки зменшиться на 1 одиницю. Таким чином, замість точок (-1, 1) і (1, 1) Ви отримаєте точки (-1, 0) і (1, 0) (і так далі).
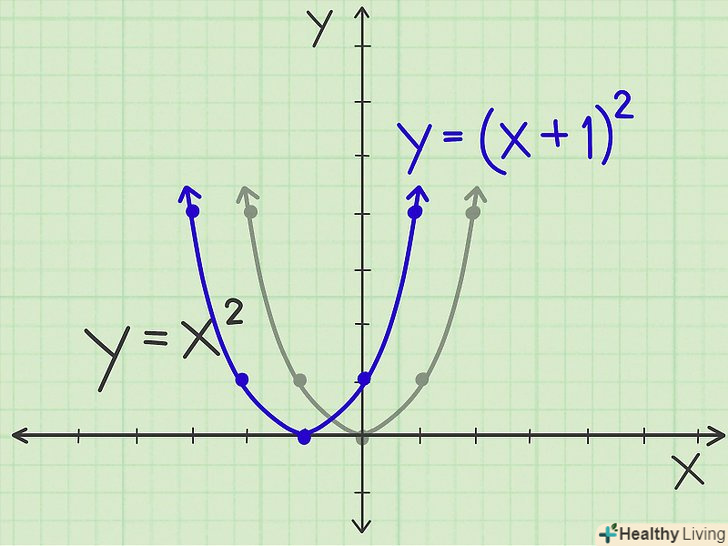
Зсув вниз. перепишіть рівняння так:y = x2 -1 , тобто парабола зрушиться вниз на 1 одиницю (вершина нової параболи має координати (0, -1)). Нова парабола матиме таку ж форму, як і вихідна, але координата «у» кожної точки зменшиться на 1 одиницю. Таким чином, замість точок (-1, 1) і (1, 1) Ви отримаєте точки (-1, 0) і (1, 0) (і так далі). Зсув вліво. перепишіть рівняння так: y = (x+1)2, тобто парабола зрушиться вліво на 1 одиницю (вершина нової параболи має координати (-1,0)). Нова парабола матиме таку ж форму, як і вихідна, але координата «х» кожної точки зменшиться на 1 одиницю. Таким чином, замість точок (-1, 1) і (1, 1) Ви отримаєте точки (-2, 1) і (0, 1) (і так далі).
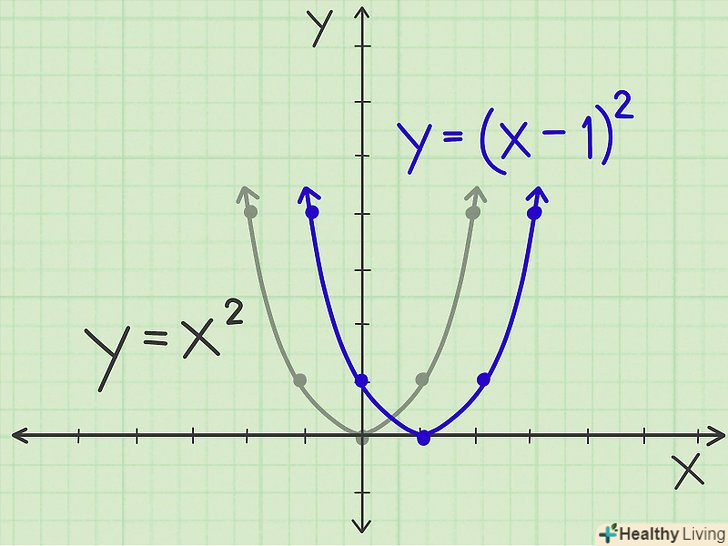
Зсув вліво. перепишіть рівняння так: y = (x+1)2, тобто парабола зрушиться вліво на 1 одиницю (вершина нової параболи має координати (-1,0)). Нова парабола матиме таку ж форму, як і вихідна, але координата «х» кожної точки зменшиться на 1 одиницю. Таким чином, замість точок (-1, 1) і (1, 1) Ви отримаєте точки (-2, 1) і (0, 1) (і так далі). Зрушення вправо. перепишіть рівняння так: y = (x-1)2, тобто парабола зрушиться вправо на 1 одиницю (вершина нової параболи має координати (1,0)). Нова парабола матиме таку ж форму, як і вихідна, але координата «х» кожної точки збільшиться на 1 одиницю. Таким чином, замість точок (-1, 1) і (1, 1) Ви отримаєте точки (0, 1) і (2, 1) (і так далі).
Зрушення вправо. перепишіть рівняння так: y = (x-1)2, тобто парабола зрушиться вправо на 1 одиницю (вершина нової параболи має координати (1,0)). Нова парабола матиме таку ж форму, як і вихідна, але координата «х» кожної точки збільшиться на 1 одиницю. Таким чином, замість точок (-1, 1) і (1, 1) Ви отримаєте точки (0, 1) і (2, 1) (і так далі).
Джерела
- Http://www.mathsisfun.com/definitions/parabola.html
- Http://www.sparknotes.com/math/algebra1/quadratics/section1.rhtml
- Http://www.purplemath.com/modules/grphquad.htm
- Http://www.mathsisfun.com/geometry/parabola.html
- ↑ Http://www.mathsisfun.com/definitions/parabola.html
- ↑ Http://www.purplemath.com/modules/grphquad.htm
- ↑ Http://www.purplemath.com/modules/grphquad.htm
- ↑ Http://www.purplemath.com/modules/grphquad.htm
- ↑ Http://www.sparknotes.com/math/algebra1/quadratics/section1.rhtml