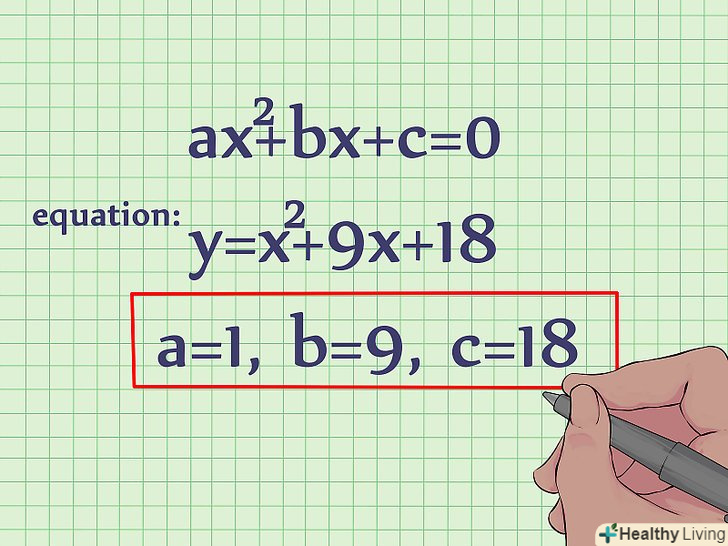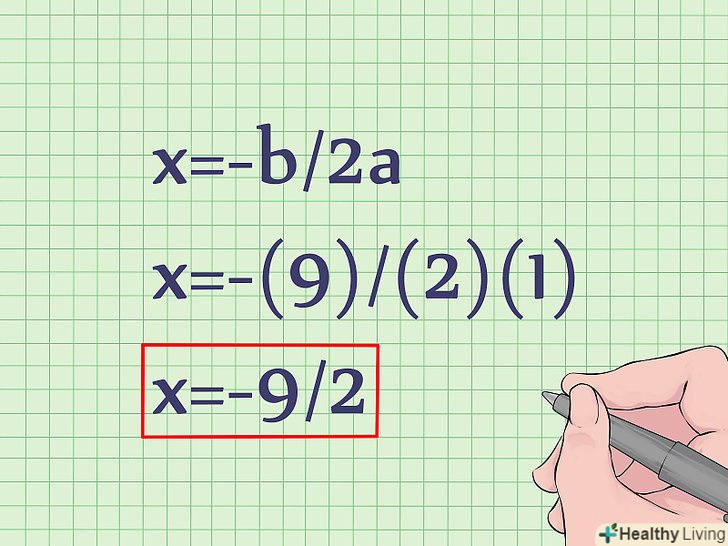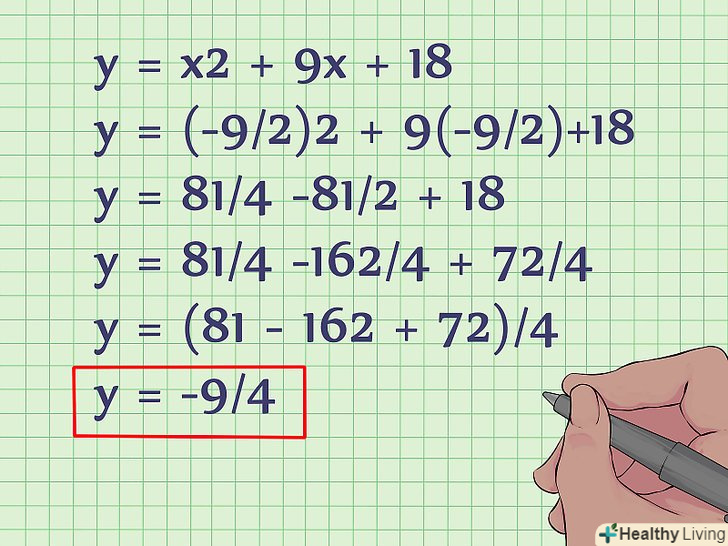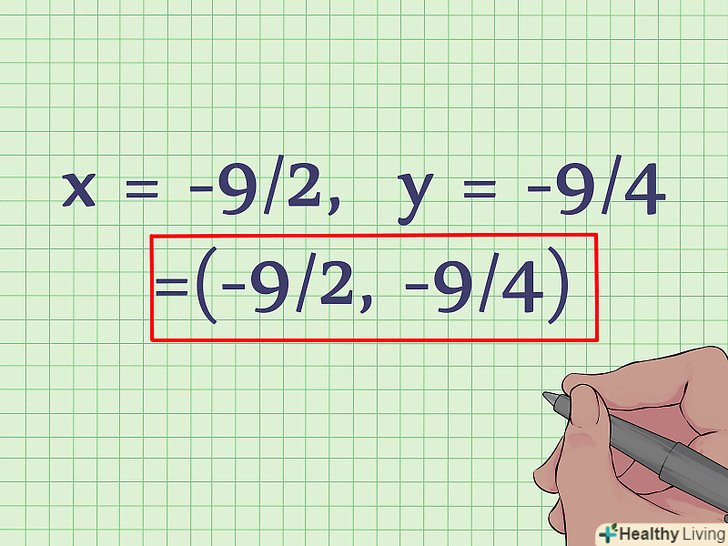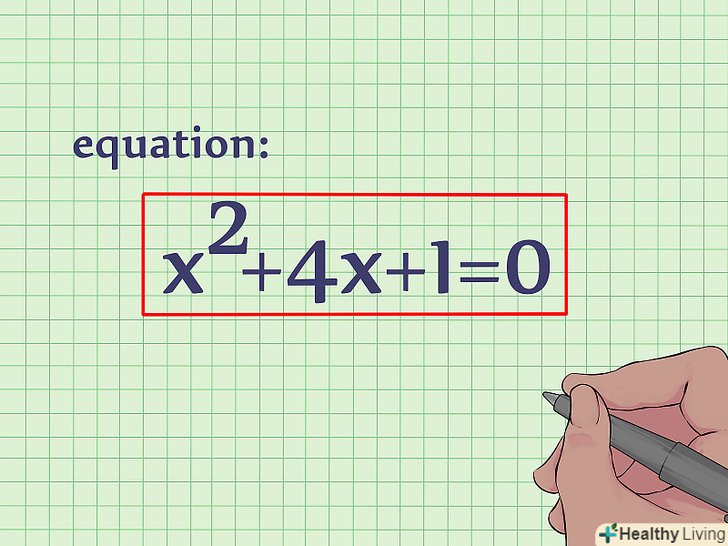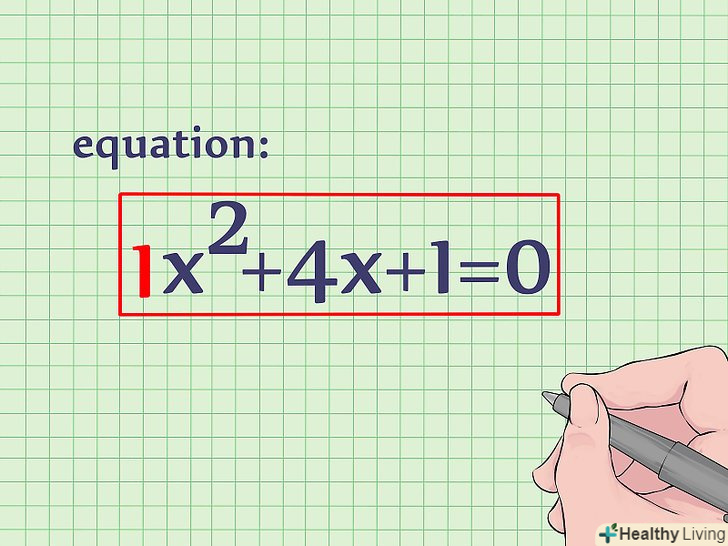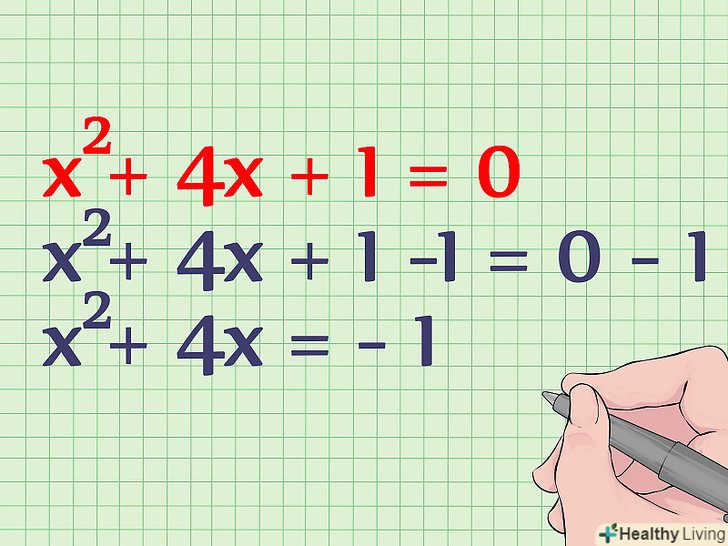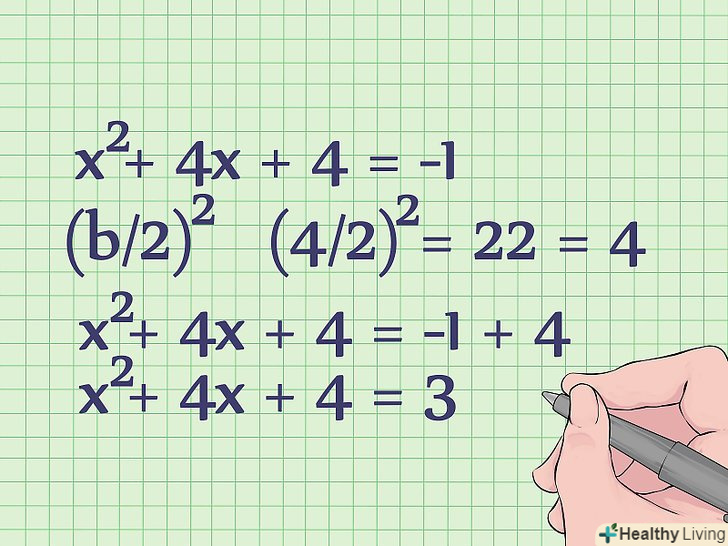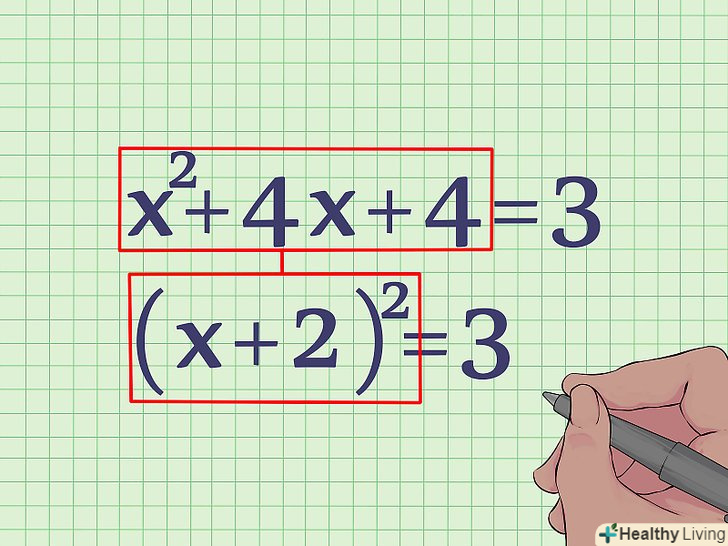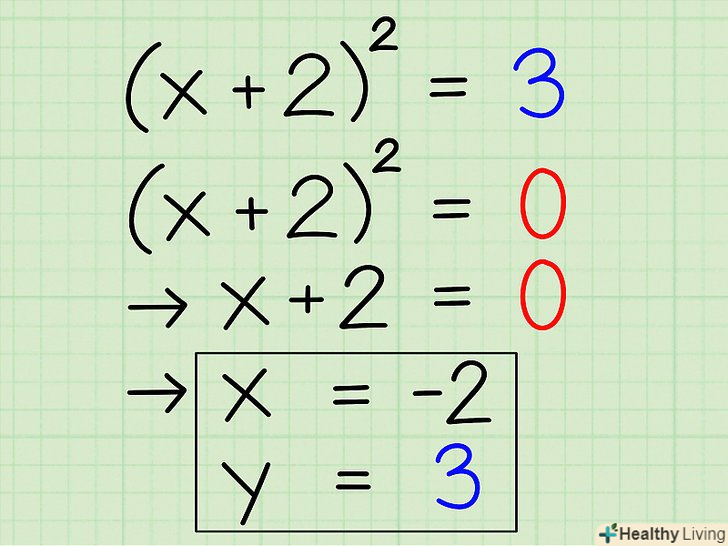Вершина параболиквадратного рівняння - це найвища або найнижча її точка. Щоб знайти вершину параболи, ви можете скористатися спеціальною формулою або методом Доповнення до повного квадрата. Нижче описано, як це зробити.
Кроки
Метод1 З 2:
Формула для знаходження вершини
Метод1 З 2:
 Знайдіть величини a, b, і c. у квадратному рівнянні коефіцієнт приx2 = a, приx = b, постійна (коефіцієнт без змінної) = c. наприклад, візьмемо рівняння:y = x2 + 9x + 18. тут a = 1, b = 9, and c = 18.[1]
Знайдіть величини a, b, і c. у квадратному рівнянні коефіцієнт приx2 = a, приx = b, постійна (коефіцієнт без змінної) = c. наприклад, візьмемо рівняння:y = x2 + 9x + 18. тут a = 1, b = 9, and c = 18.[1] Скористайтеся формулою для обчислення значення координати x вершини. Вершина також є точкою симетрії параболи. Формула для знаходження координати x параболи: x = -b/2a.підставте в неї відповідні значення для обчислення x.
Скористайтеся формулою для обчислення значення координати x вершини. Вершина також є точкою симетрії параболи. Формула для знаходження координати x параболи: x = -b/2a.підставте в неї відповідні значення для обчислення x.- X=-b/2a
- X=-(9)/(2)(1)
- X=-9/2
 Підставте знайдене значення x у вихідне рівняння для обчислення значення y. Тепер, коли вам відомо значення x, просто підставте його у вихідне рівняння для знаходження y. Таким чином, формулу для знаходження вершини параболи можна записати у вигляді функції: (x, y) = [(-b/2A), f(-b/2a)]. Це означає, що для знаходження y необхідно спочатку знайти x за формулою, а потім підставити значення x у вихідне рівняння. Ось, як це робиться:
Підставте знайдене значення x у вихідне рівняння для обчислення значення y. Тепер, коли вам відомо значення x, просто підставте його у вихідне рівняння для знаходження y. Таким чином, формулу для знаходження вершини параболи можна записати у вигляді функції: (x, y) = [(-b/2A), f(-b/2a)]. Це означає, що для знаходження y необхідно спочатку знайти x за формулою, а потім підставити значення x у вихідне рівняння. Ось, як це робиться:- Y = x2 + 9x + 18
- Y = (-9/2)2 + 9(-9/2) +18
- Y = 81/4 -81/2 + 18
- Y = 81/4 -162/4 + 72/4
- Y = (81 - 162 + 72)/4
- Y = -9/4
 Запишіть значення x і y у вигляді пари координат.тепер, коли вам відомо, що x = -9/2, А y = -9/4, запишіть їх як координати у вигляді: (-9/2, -9/4). Вершина параболи знаходиться за координатами (-9/2, -9/4). Якщо вам потрібно намалювати цю параболу, то її вершина лежить в нижній точці, так як коефіцієнт при x2 позитивний.
Запишіть значення x і y у вигляді пари координат.тепер, коли вам відомо, що x = -9/2, А y = -9/4, запишіть їх як координати у вигляді: (-9/2, -9/4). Вершина параболи знаходиться за координатами (-9/2, -9/4). Якщо вам потрібно намалювати цю параболу, то її вершина лежить в нижній точці, так як коефіцієнт при x2 позитивний.
Метод2 З 2:
Доповнення до повного квадрата
Метод2 З 2:
 Запишіть рівняння.Доповнення до повного квадрата-ще один спосіб знайти вершину параболи. Застосувавши цей метод, ви знайдете координати x і y відразу, без необхідності підставляти x в вихідне рівняння. Наприклад, дано рівняння: x 2 + 4x + 1 = 0.[2]
Запишіть рівняння.Доповнення до повного квадрата-ще один спосіб знайти вершину параболи. Застосувавши цей метод, ви знайдете координати x і y відразу, без необхідності підставляти x в вихідне рівняння. Наприклад, дано рівняння: x 2 + 4x + 1 = 0.[2] Розділіть кожен коефіцієнт на коефіцієнт при x2. у нашому випадку коефіцієнт при x2 дорівнює 1, тому ми можемо пропустити цей крок. Поділ на 1 нічого не змінить.
Розділіть кожен коефіцієнт на коефіцієнт при x2. у нашому випадку коефіцієнт при x2 дорівнює 1, тому ми можемо пропустити цей крок. Поділ на 1 нічого не змінить. Перенесіть постійну в праву частину рівняння. постійна-коефіцієнт без змінної. Тут це 1. Перенесіть 1 вправо шляхом віднімання 1 з обох частин рівняння. Ось, як це зробити:[3]
Перенесіть постійну в праву частину рівняння. постійна-коефіцієнт без змінної. Тут це 1. Перенесіть 1 вправо шляхом віднімання 1 з обох частин рівняння. Ось, як це зробити:[3]- X2 + 4x + 1 = 0
- X2 + 4x + 1 -1 = 0 - 1
- X2 + 4x = - 1
 Доповніть до повного квадрата ліву частину рівняння. для цього просто знайдіть (b/2)2 і додайте результат до обох частин рівняння. Підставте 4 замість b , так як 4X — це коефіцієнт B нашого рівняння.
Доповніть до повного квадрата ліву частину рівняння. для цього просто знайдіть (b/2)2 і додайте результат до обох частин рівняння. Підставте 4 замість b , так як 4X — це коефіцієнт B нашого рівняння.- (4/2)2 = 22 = 4. Тепер додайте 4 до обох частин рівняння і отримаєте:
- X2 + 4x + 4 = -1 + 4
- X2 + 4x + 4 = 3
- (4/2)2 = 22 = 4. Тепер додайте 4 до обох частин рівняння і отримаєте:
 Спрощуємо ліву частину рівняння. ми бачимо, що x2 + 4x + 4 — повний квадрат. Він може бути записаний у вигляді: (x + 2)2 = 3
Спрощуємо ліву частину рівняння. ми бачимо, що x2 + 4x + 4 — повний квадрат. Він може бути записаний у вигляді: (x + 2)2 = 3 Використовуйте його для знаходження координат x і y. ви можете знайти x, просто прирівнявши (x + 2)2 до 0. Тепер, коли (x + 2)2 = 0, обчислюємо x: x =-2. Координата y-це постійна в правій частині повного квадрата. Отже, y = 3. Вершина параболи рівняння x2 + 4x + 1 = (-2, 3)
Використовуйте його для знаходження координат x і y. ви можете знайти x, просто прирівнявши (x + 2)2 до 0. Тепер, коли (x + 2)2 = 0, обчислюємо x: x =-2. Координата y-це постійна в правій частині повного квадрата. Отже, y = 3. Вершина параболи рівняння x2 + 4x + 1 = (-2, 3)
Поради
- Правильно визначайте a, b, і C.
- Записуйте попередні обчислення. Це не тільки допоможе в процесі роботи, але і дозволить побачити, де зроблені помилки.
- Не порушуйте порядок обчислень.
Попередження
- Перевірте вашу відповідь!
- Переконайтеся, що Ви знаєте, як визначити коефіцієнта a, b, і C. Якщо ви не знаєте, відповідь буде неправильною.
- Непанікуйте - вирішення таких завдань вимагає практики.
Що вам знадобиться
- папір або комп'ютер
- Калькулятор