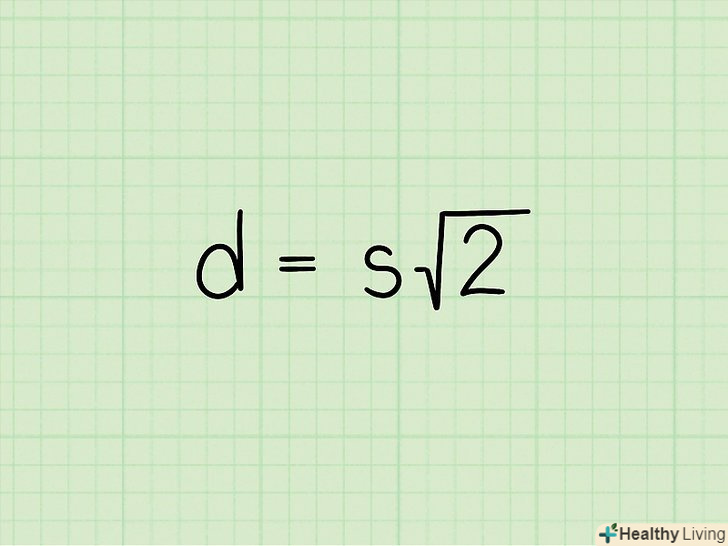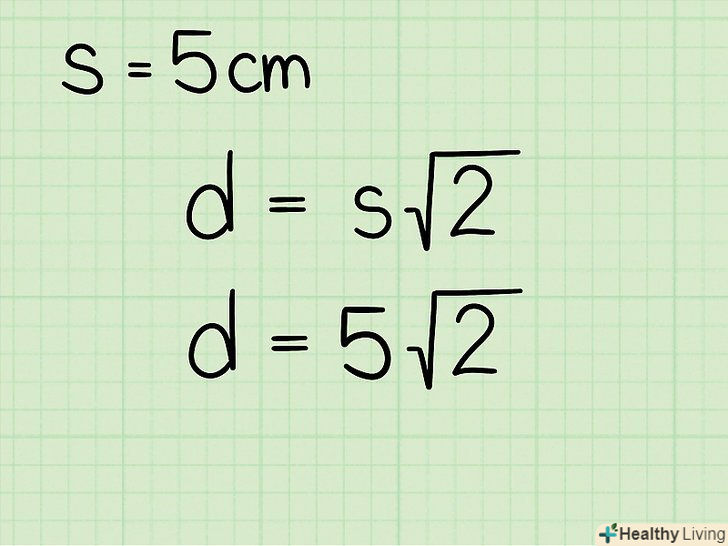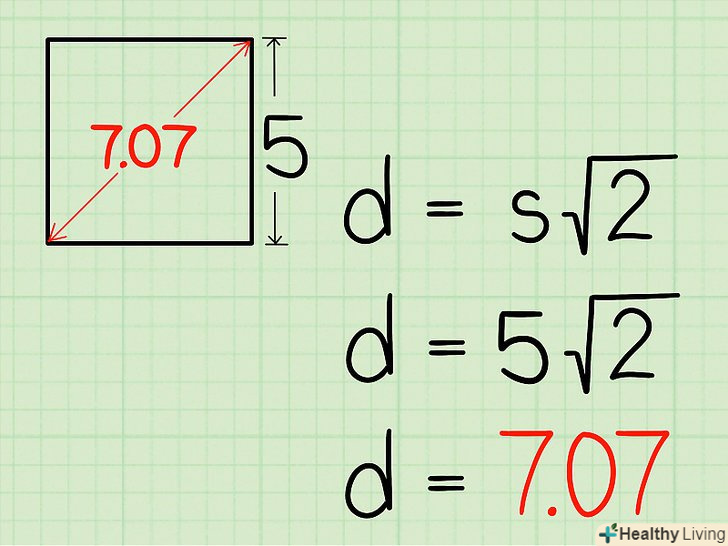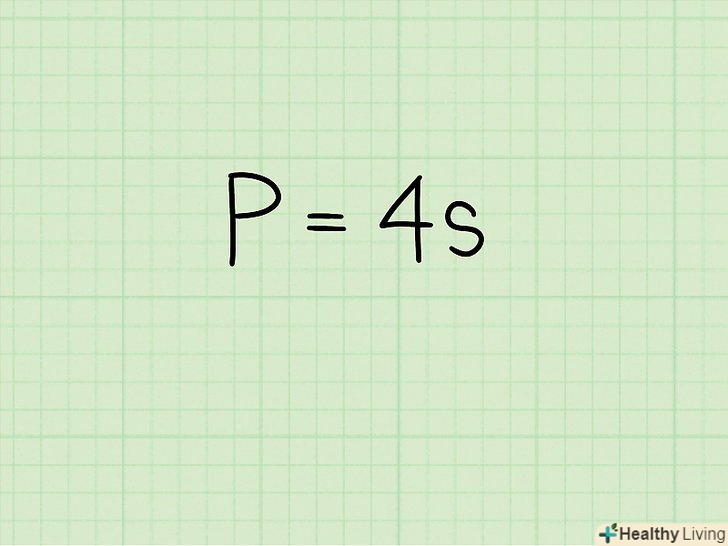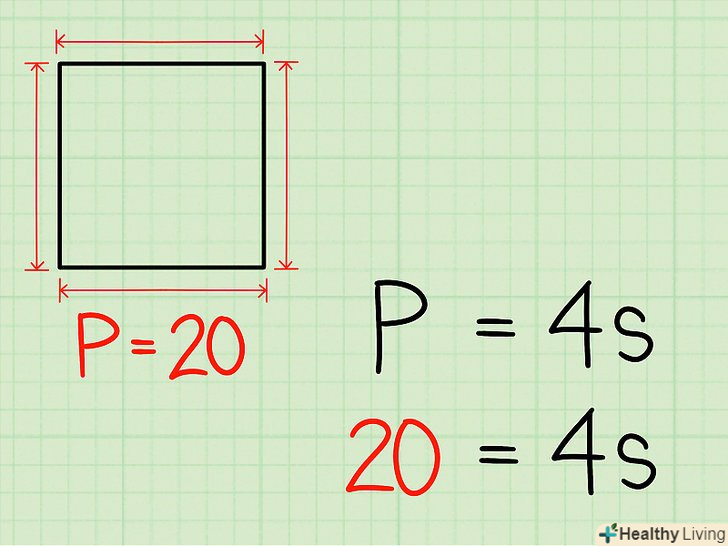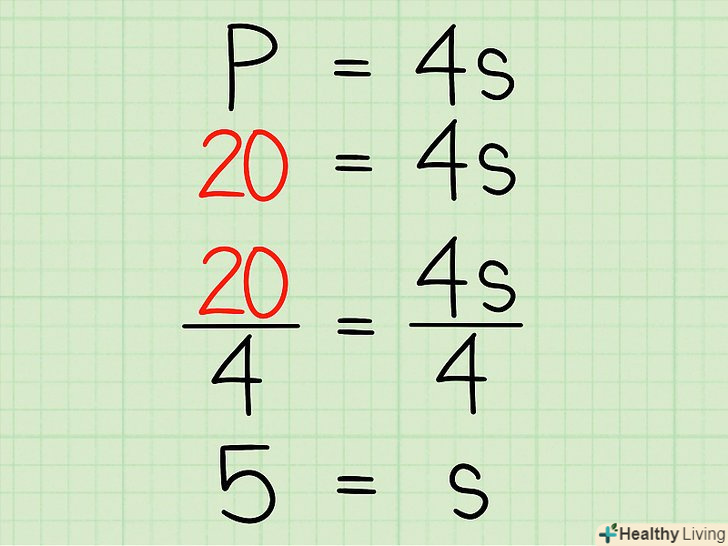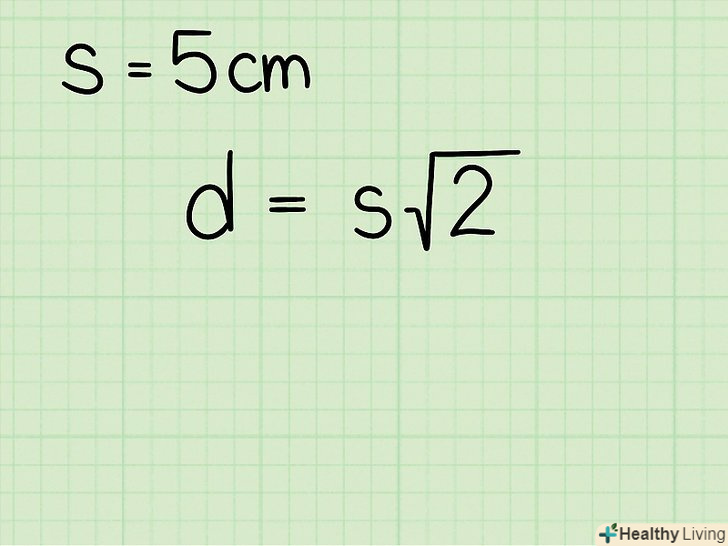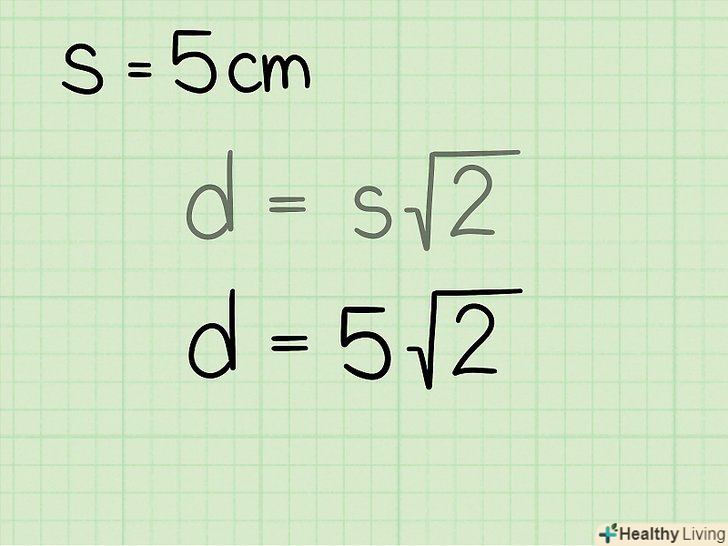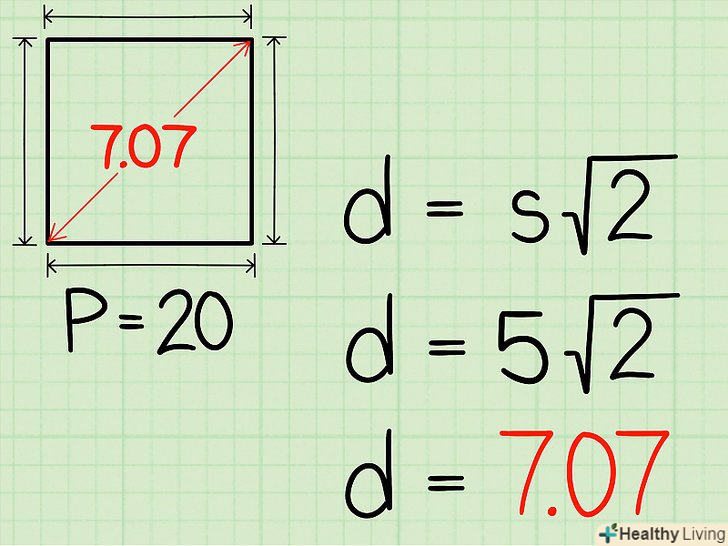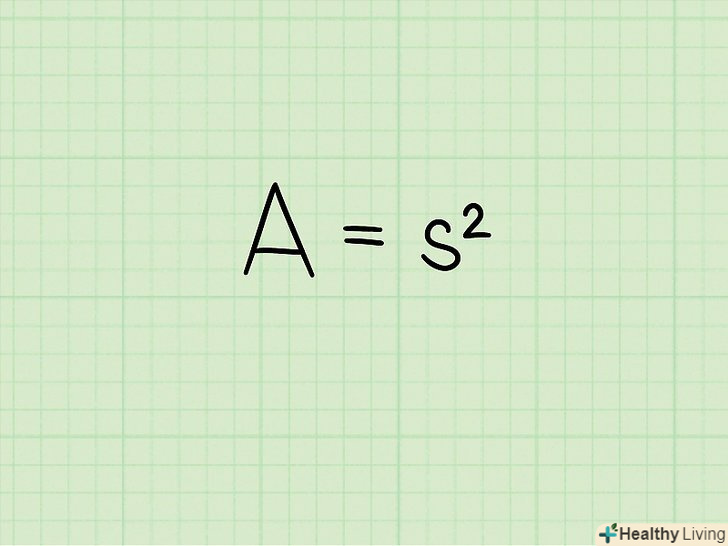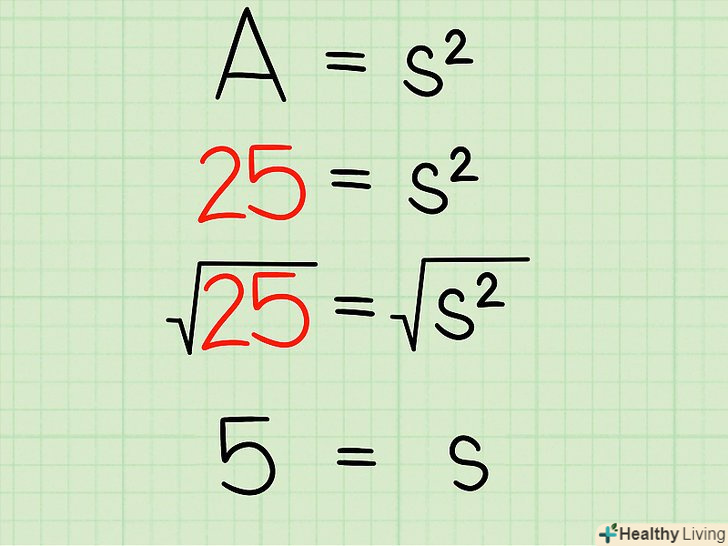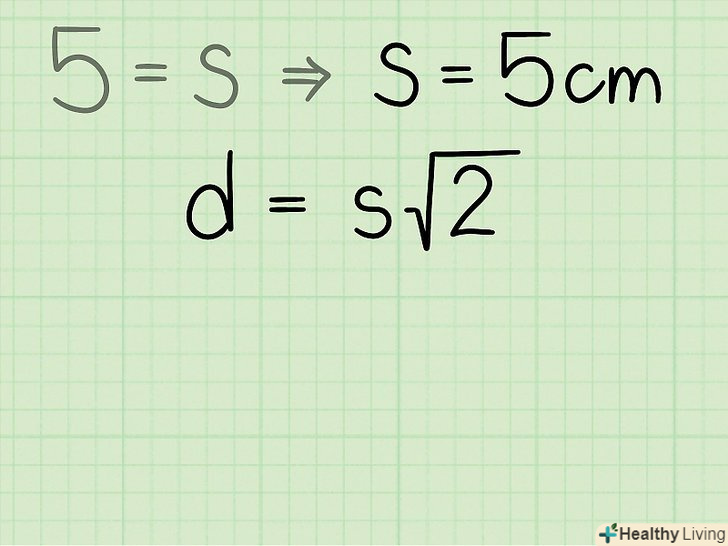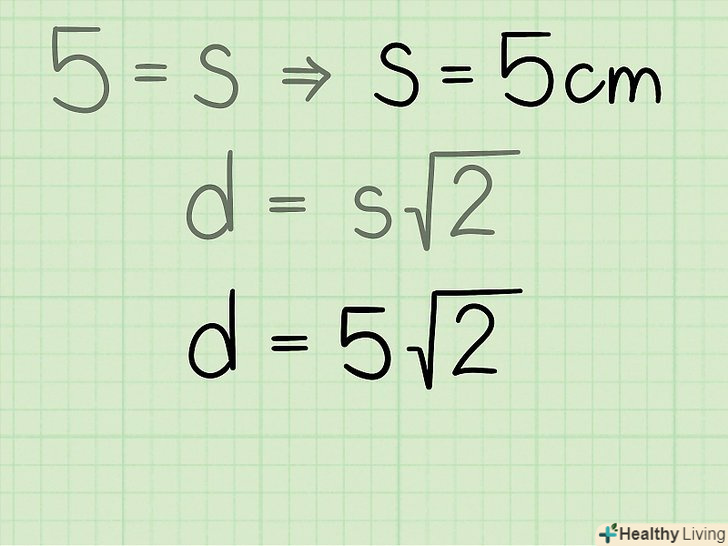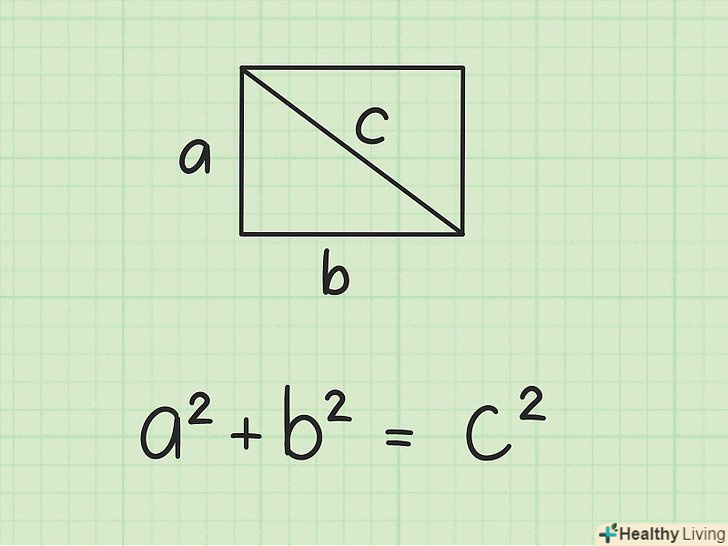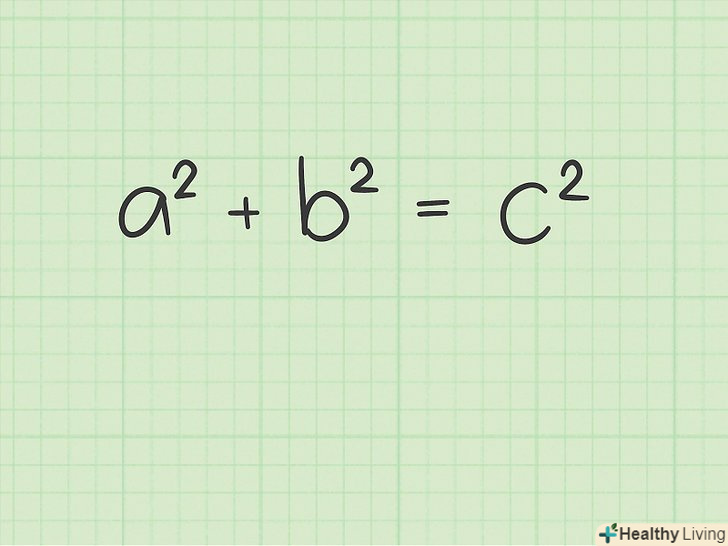Діагональ квадрата - це відрізок, який з'єднує протилежні кути квадрата і проходить через його центр. Щоб обчислити діагональ квадрата, скористайтеся формулою, де
— сторона квадрата. У завданнях потрібно знайти діагональ квадрата за даним значенням іншої величини, наприклад, периметра або площі. У цих випадках необхідно використовувати інші формули, щоб спочатку обчислити сторону квадрата, а потім – його діагональ.
Кроки
Метод1З 3:
Обчислення діагоналі по відомій стороні квадрата
Метод1З 3:
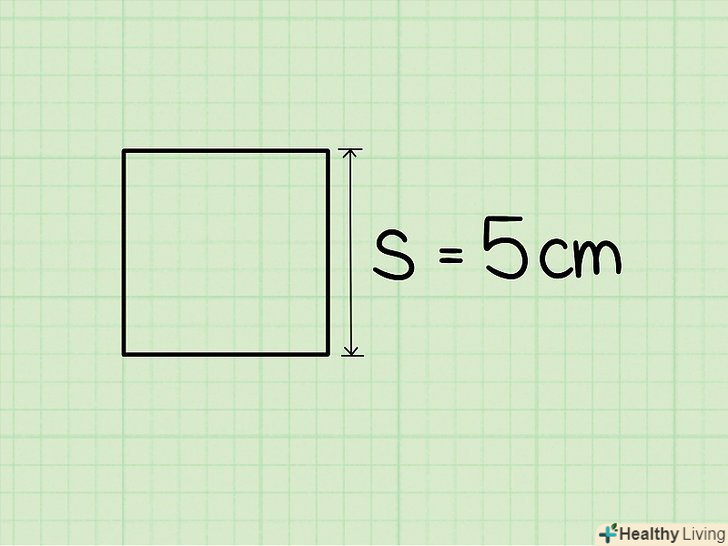
 Знайдіть довжину сторони квадрата.швидше за все, значення довжини сторони квадрата буде дано в умові завдання. Якщо ж ви працюєте з реальним предметом, виміряйте його сторону за допомогою лінійки або рулетки. Так як у квадрата всі сторони рівні, виміряйте або знайдіть довжину будь-якої сторони. Якщо довжина сторони квадрата невідома, цим методом користуватися не можна.
Знайдіть довжину сторони квадрата.швидше за все, значення довжини сторони квадрата буде дано в умові завдання. Якщо ж ви працюєте з реальним предметом, виміряйте його сторону за допомогою лінійки або рулетки. Так як у квадрата всі сторони рівні, виміряйте або знайдіть довжину будь-якої сторони. Якщо довжина сторони квадрата невідома, цим методом користуватися не можна.- Наприклад, дано квадрат зі стороною 5 см.
 Запишіть формулу
Запишіть формулу. у цій формулою
— діагональ квадрата,
— сторона квадрата.[1]&#gt;
- Ця формула виводиться з теореми Піфагора (
. Діагональ ділить квадрат на два рівних прямокутних трикутника, тобто сторони квадрата можна використовувати для обчислення діагоналі квадрата, яка являє собою гіпотенузу прямокутного трикутника.
- Ця формула виводиться з теореми Піфагора (
 Підставте в формулу значення довжини сторони квадрата. тобто дане значення потрібно підставити замість
Підставте в формулу значення довжини сторони квадрата. тобто дане значення потрібно підставити замість.
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула запишеться так:
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула запишеться так:
 Помножте сторону квадрата на
Помножте сторону квадрата на, щоб знайти діагональ квадрата.обчислення краще виконати на калькуляторі, щоб отримати точну відповідь. Якщо калькулятора немає, округлите
до 1,414.
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула записується у вигляді
Таким чином, діагональ квадрата дорівнює 7,07 см.
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула записується у вигляді
Метод2 З 3:
Обчислення діагоналі по відомому периметру квадрата
Метод2 З 3:
 Запишіть формулу для обчислення периметра квадрата. Формула:
Запишіть формулу для обчислення периметра квадрата. Формула:, де
— периметр квадрата,
— сторона квадрата.[2]
- Цей спосіб застосовується тільки в тому випадку, коли дано периметр квадрата.
- Щоб знайти діагональ квадрата, спочатку потрібно обчислити сторону квадрата
— для цього скористайтеся формулою для обчислення периметра квадрата.
 Підставте в формулу значення периметра квадрата. тобто дане значення потрібно підставити замість
Підставте в формулу значення периметра квадрата. тобто дане значення потрібно підставити замість.
- Наприклад, периметр квадрата дорівнює 20 см. Запишіть формулу так:
- Наприклад, периметр квадрата дорівнює 20 см. Запишіть формулу так:
 Знайдіть
Знайдіть.для цього розділіть кожну сторону рівняння на 4. В результаті буде обчислена сторона квадрата.
- У нашому прикладі:
- У нашому прикладі:
 Запишіть формулу
Запишіть формулу. у цій формулою
— діагональ квадрата,
— сторона квадрата.[3]
- Ця формула виводиться з теореми Піфагора (
. Діагональ ділить квадрат на два рівних прямокутних трикутника, тобто сторони квадрата можна використовувати для обчислення діагоналі квадрата, яка являє собою гіпотенузу прямокутного трикутника.
- Ця формула виводиться з теореми Піфагора (
 Підставте в формулу значення довжини сторони квадрата. тобто дане значення потрібно підставити замість
Підставте в формулу значення довжини сторони квадрата. тобто дане значення потрібно підставити замість.
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула запишеться так:
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула запишеться так:
 Помножте сторону квадрата на
Помножте сторону квадрата на, щоб знайти діагональ квадрата.обчислення краще виконати на калькуляторі, щоб отримати точну відповідь. Якщо калькулятора немає, округлите
до 1,414.
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула записується у вигляді
Таким чином, діагональ квадрата дорівнює 7,07 см.
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула записується у вигляді
Метод3 З 3:
Обчислення діагоналі по відомій площі квадрата
Метод3 З 3:
 Запишіть формулу для обчислення площі квадрата. Формула:
Запишіть формулу для обчислення площі квадрата. Формула:, де
— площа квадрата,
— сторона квадрата.[4]
- Цей спосіб застосовується тільки в тому випадку, коли дана площа квадрата.
- Щоб знайти діагональ квадрата, спочатку потрібно обчислити сторону квадрата
— для цього скористайтеся формулою для обчислення площі квадрата.
 У формулу підставте значення площі квадрата. тобто дане значення потрібно підставити замість
У формулу підставте значення площі квадрата. тобто дане значення потрібно підставити замість.
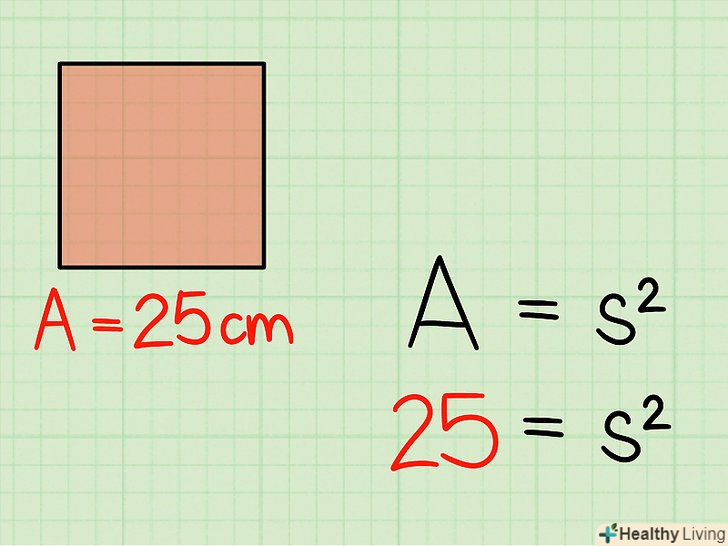
- Наприклад, площа квадрата дорівнює 25 см2. Запишіть формулу так:
.
- Наприклад, площа квадрата дорівнює 25 см2. Запишіть формулу так:
 Знайдіть
Знайдіть.для цього витягніть квадратний корінь із значення площі квадрата. В результаті буде обчислена сторона квадрата. Скористайтеся калькулятором, щоб витягти квадратний корінь. Якщо квадратний корінь потрібно витягти вручну, прочитайте цю статтю.
- У нашому прикладі:
- У нашому прикладі:
 Запишіть формулу
Запишіть формулу. у цій формулою
— діагональ квадрата,
— сторона квадрата.[5]
- Ця формула виводиться з теореми Піфагора (
. Діагональ ділить квадрат на два рівних прямокутних трикутника, тобто сторони квадрата можна використовувати для обчислення діагоналі квадрата, яка являє собою гіпотенузу прямокутного трикутника.
- Ця формула виводиться з теореми Піфагора (
 Підставте в формулу значення довжини сторони квадрата. тобто дане значення потрібно підставити замість
Підставте в формулу значення довжини сторони квадрата. тобто дане значення потрібно підставити замість.
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула запишеться так:
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула запишеться так:
 Помножте сторону квадрата на
Помножте сторону квадрата на, щоб знайти діагональ квадрата.обчислення краще виконати на калькуляторі, щоб отримати точну відповідь. Якщо калькулятора немає, округлите
до 1,414.
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула записується у вигляді
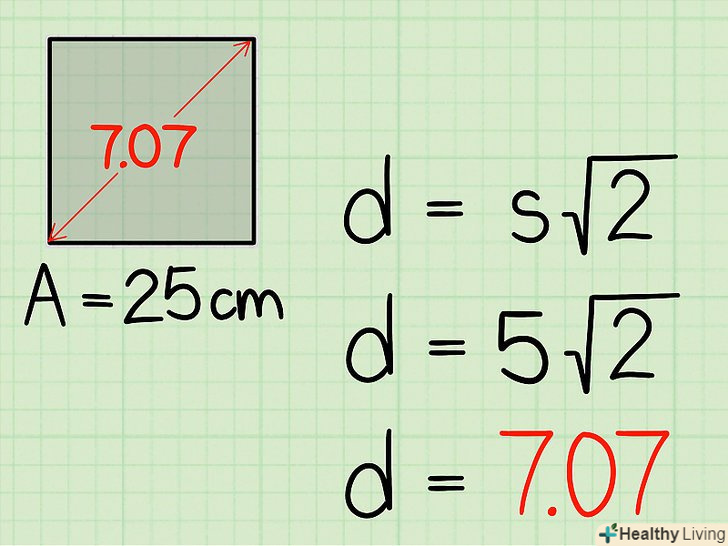
Таким чином, діагональ квадрата дорівнює 7,07 см.
- Наприклад, якщо сторона квадрата дорівнює 5 см, формула записується у вигляді
Що вам знадобиться
- Калькулятор