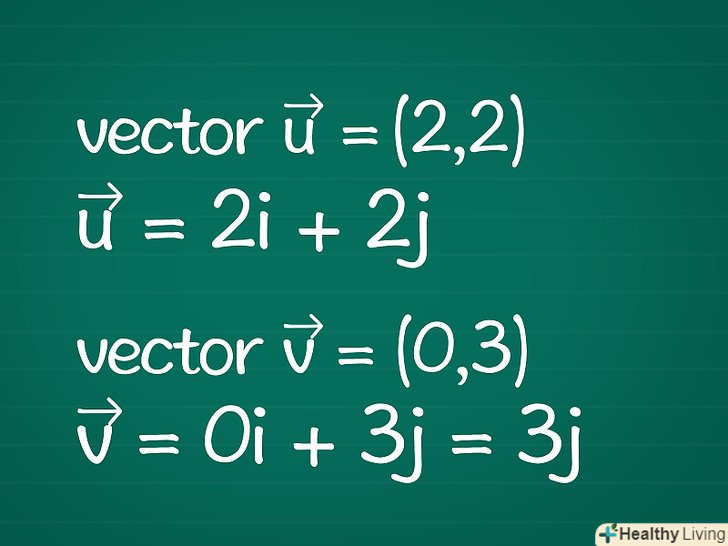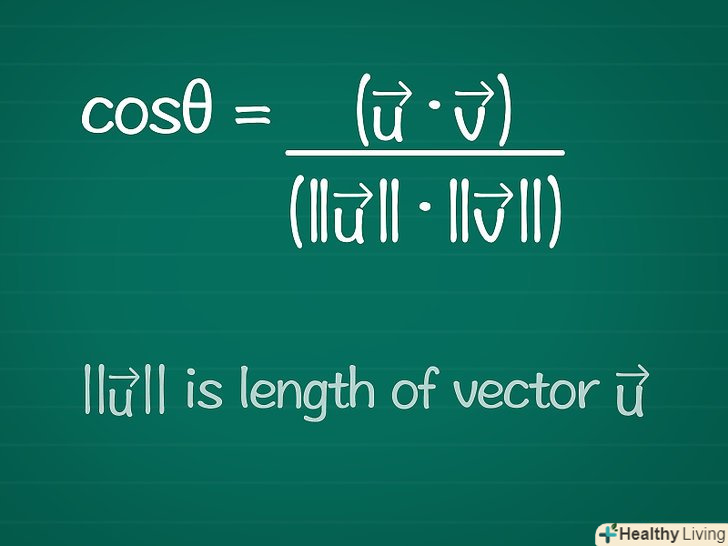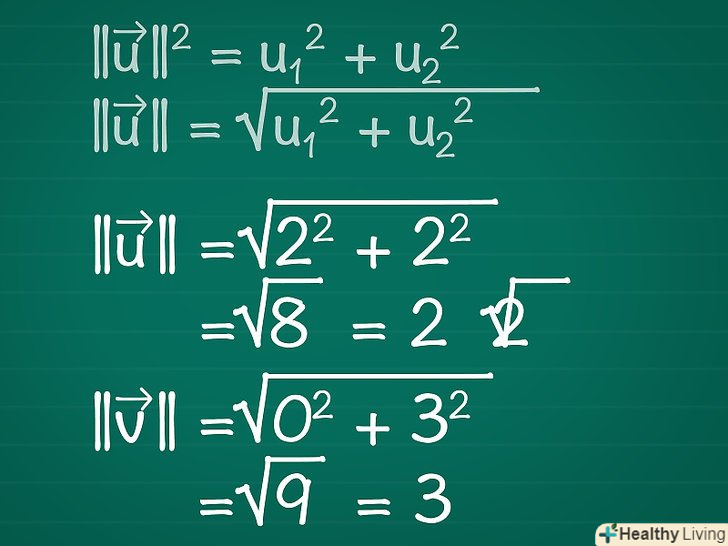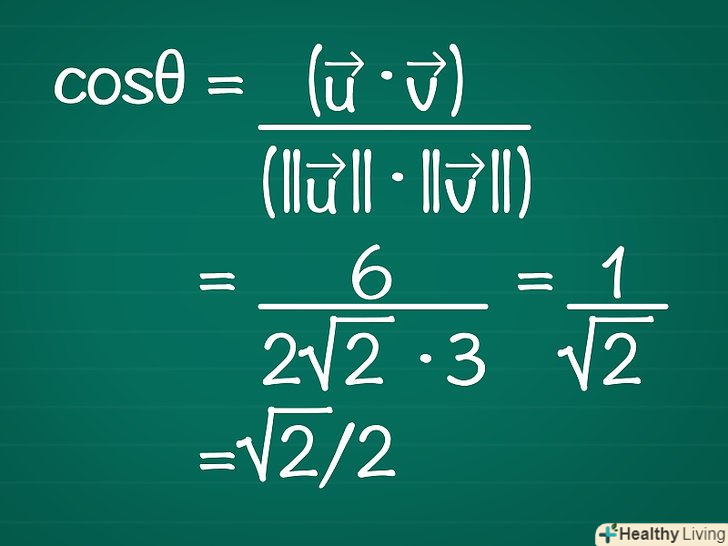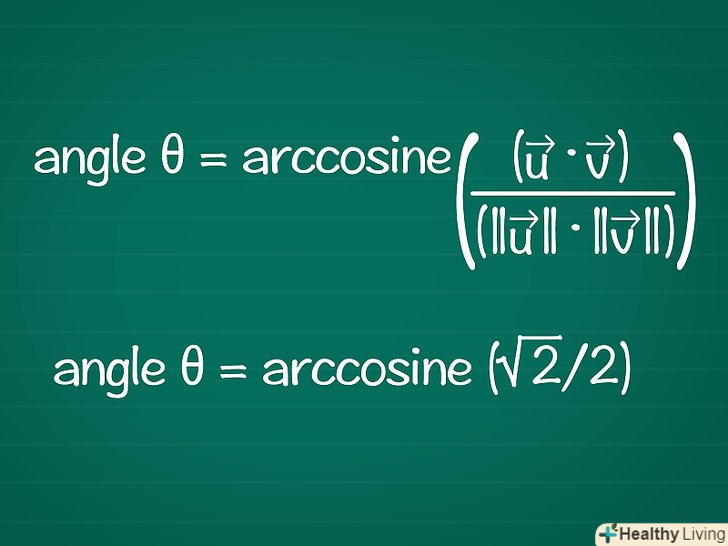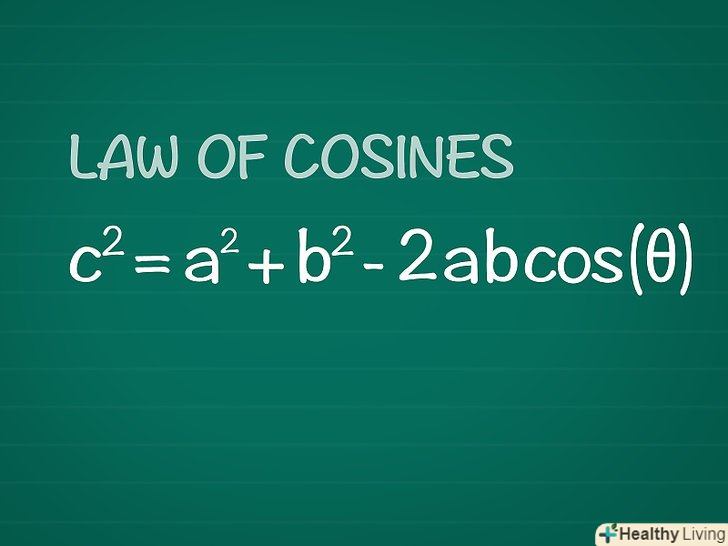Математики та фізики часто обчислюють кут між двома даними векторами. Для обчислення такого кута застосовують формулу, яка заснована на скалярному добутку векторів. Формула може застосовуватися для векторів як у двовимірному, так і в багатовимірному просторах.
Кроки
Частина1 З 2:
Знаходження кута між двома векторами
Частина1 З 2:
 Запишіть інформацію про два вектори.у цій статті ми будемо розглядати вектори в двовимірному просторі.[1] якщо довжини векторів вам дані, пропустіть деякі з наступних кроків.
Запишіть інформацію про два вектори.у цій статті ми будемо розглядати вектори в двовимірному просторі.[1] якщо довжини векторів вам дані, пропустіть деякі з наступних кроків.- Приклад. Дано вектори
= (2,2) і
= (0,3). Ці вектори також можна записати у вигляді
= 2i + 2j
= 0i + 3j = 3j.
- Наш приклад розглядає двовимірні вектори, але описані нижче інструкції можна застосовувати і до багатовимірних векторів.
- Приклад. Дано вектори
 Запишіть формулу.щоб знайти кут θ між двома векторами, почніть з знаходження косинуса цього кута. (Про цю формулу ми розповімо в наступному розділі.) [2]
Запишіть формулу.щоб знайти кут θ між двома векторами, почніть з знаходження косинуса цього кута. (Про цю формулу ми розповімо в наступному розділі.) [2]- Cosθ = (
•
) / (||
|| ||
||)
- ||
|| – це довжина вектора
.
•
– це скалярний добуток двох векторів.
- Cosθ = (
 Обчисліть скалярний добуток двох векторів. [3] для цього перемножте відповідні компоненти двох векторів і складіть отримані значення.[4]
Обчисліть скалярний добуток двох векторів. [3] для цього перемножте відповідні компоненти двох векторів і складіть отримані значення.[4]•
= u1v1 + u2v2, де u = (u1, u2). Якщо ваші вектори мають більше двох компонент, просто продовжуйте додавати твори їх компонентів: + u3v3 + u4v4...
- Таким чином, у двомірному векторі,||u|| = √(u12 + u22).
- У нашому прикладі:
•
= u1v1 + u2v2 = (2)(0) + (2)(3) = 0 + 6 = 6.
 Обчисліть довжину кожного вектора. намалюйте прямокутний трикутник, сторонами якого буде сам вектор (гіпотенуза), його х-компонента і його у-компонента (катети). Тепер знайдіть довжину вектора за допомогою теореми Піфагора (її можна застосовувати до багатокомпонентних векторів).[5]
Обчисліть довжину кожного вектора. намалюйте прямокутний трикутник, сторонами якого буде сам вектор (гіпотенуза), його х-компонента і його у-компонента (катети). Тепер знайдіть довжину вектора за допомогою теореми Піфагора (її можна застосовувати до багатокомпонентних векторів).[5]- ||u||2 = u12 + u22. Якщо ваші вектори мають більше двох компонент, просто продовжуйте додавати: + u32 + u42 + ...
- Таким чином, для двовимірного вектора:/ / u / / = √(u12 + u22).
- У нашому прикладі: ||
|| = √(22 + 22) = √(8) = 2√2. ||
|| = √(02 + 32) = √(9) = 3.
 Підставте знайдені значення (довжину векторів і їх скалярний добуток) у формулу cosθ = (
Підставте знайдені значення (довжину векторів і їх скалярний добуток) у формулу cosθ = (•
) / (||
|| ||
||).
- У нашому прикладі: cosθ =6 / (2√2 * 3) = 1 / √2 = √2 / 2.
 Знайдіть кут по його косинусу. ви можете використовувати кнопку Arccos або Cos-1 на калькуляторі, щоб знайти кут θ за відомим значенням cosθ. У деяких випадках ви можете знайти Кут, користуючись одиничною окружністю.
Знайдіть кут по його косинусу. ви можете використовувати кнопку Arccos або Cos-1 на калькуляторі, щоб знайти кут θ за відомим значенням cosθ. У деяких випадках ви можете знайти Кут, користуючись одиничною окружністю.- У нашому прикладі, cosθ = √2/2. На одиничному колі це значення відповідає куту 'θ = π / 4 або 45º
- Поєднуючи все, отримуємо формулу: кут θ = arccosin ((
•
) / (||
|| ||
||))
'.
Частина2 З 2:
Формула для обчислення кута
Частина2 З 2:
 Ця формула була виведена для визначення скалярного добутку двох векторів і кута між ними.[6] але цю формулу не взяли»зі стелі". Вона була виведена, грунтуючись на геометричних принципах.
Ця формула була виведена для визначення скалярного добутку двох векторів і кута між ними.[6] але цю формулу не взяли»зі стелі". Вона була виведена, грунтуючись на геометричних принципах.- Наведені нижче приклади розглядають двовимірні вектори (тому що з ними простіше працювати). Вектори з трьома або більше компонентами мають властивості, що визначаються аналогічною формулою.
 Теорема косинусів. розгляньте довільний трикутник з кутом θ між сторонами а і b і протилежною йому стороною С.Теорема косинусів говорить: c2 = a2 + b2 -2ABcos(θ).[7]
Теорема косинусів. розгляньте довільний трикутник з кутом θ між сторонами а і b і протилежною йому стороною С.Теорема косинусів говорить: c2 = a2 + b2 -2ABcos(θ).[7] З'єднайте два вектори так, щоб отримати трикутник. намалюйте два двовимірні вектори
З'єднайте два вектори так, щоб отримати трикутник. намалюйте два двовимірні векториі
з кутом θ між ними. Проведіть третій вектор так, щоб вийшов трикутник. Іншими словами, намалюйте вектор
так, щоб
+
=
. Таким чином,
=
-
.[8]
 Запишіть теорему косинусів для отриманого трикутника:
Запишіть теорему косинусів для отриманого трикутника:- ||(a - b)||2 = ||a||2 + ||b||2 - 2||a|| ||b||cos(θ)
 Перепишіть отримане рівняння через скалярний добуток двох векторів.Скалярний добуток-це множення довжини вектора "x «на проекцію вектора» y «на вектор»x". Але скалярний добуток вектора на самого себе не вимагає будь-яких проекцій.[9] Це означає, що
Перепишіть отримане рівняння через скалярний добуток двох векторів.Скалярний добуток-це множення довжини вектора "x «на проекцію вектора» y «на вектор»x". Але скалярний добуток вектора на самого себе не вимагає будь-яких проекцій.[9] Це означає, що•
= ||a||2/. Використовуйте цей факт, щоб переписати рівняння у вигляді:
- (
-
) • (
-
) =
•
+
•
- 2||a|| ||b||cos(θ)
- (
 Розкрийте дужки в лівій частині рівняння і спростіть його.
Розкрийте дужки в лівій частині рівняння і спростіть його.•
-
•
-
•
+
•
=
•
+
•
- 2||a|| ||b||cos(θ)
- -
•
-
•
= -2||a|| ||b||cos(θ)
- -2(
•
) = -2||a|| ||b||cos(θ)
•
= ||a|| ||b||cos(θ)
Поради
- Для прискорення рішення Використовуйте наступну формулу для будь-якої пари двовимірних векторів: cosθ = (u1 • v1 + u2 • v2) / (√(u12 • u22) • √(v12 • v22)).
- Якщо ви працюєте на комп'ютері в графічній програмі, вам, швидше за все потрібно тільки напрямок вектора, а не Довжина. Використовуйте