Знаходження периметра фігури-часом непросте завдання. Ця стаття навчить вас знаходити периметри наступних основних фігур: прямокутника, квадрата, кола, прямокутного трикутника, трикутника і правильного багатокутника.
Кроки
Метод1З 6:
Прямоугольник
Метод1З 6:
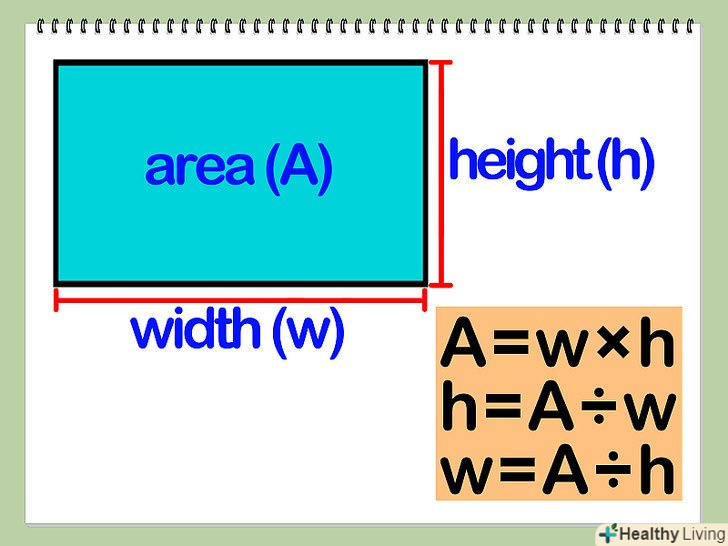
 Знайдіть довжини двох суміжних сторін: ширини і висоти. Прямокутник-фігура з чотирма сторонами, які перетинаються під прямим кутом, а дві протилежні сторони паралельні і рівні. Таким чином, дві суміжні сторони мають різну довжину (ширина і висота; якщо ширина дорівнює висоті, то така фігура – квадрат).
Знайдіть довжини двох суміжних сторін: ширини і висоти. Прямокутник-фігура з чотирма сторонами, які перетинаються під прямим кутом, а дві протилежні сторони паралельні і рівні. Таким чином, дві суміжні сторони мають різну довжину (ширина і висота; якщо ширина дорівнює висоті, то така фігура – квадрат).- Якщо дано лише одну сторону та площу прямокутника, ви можете знайти іншу сторону за формулою: A=wh, тобто h=A/w або w=A / h. Отже, якщо дано Висоту та площу, просто розділіть площу на висоту, щоб знайти ширину. Ви також можете розділити площу на ширину, щоб знайти висоту.
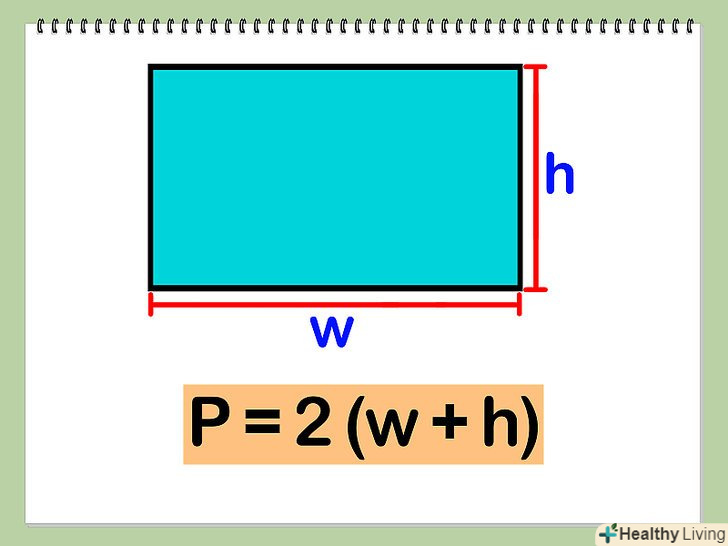
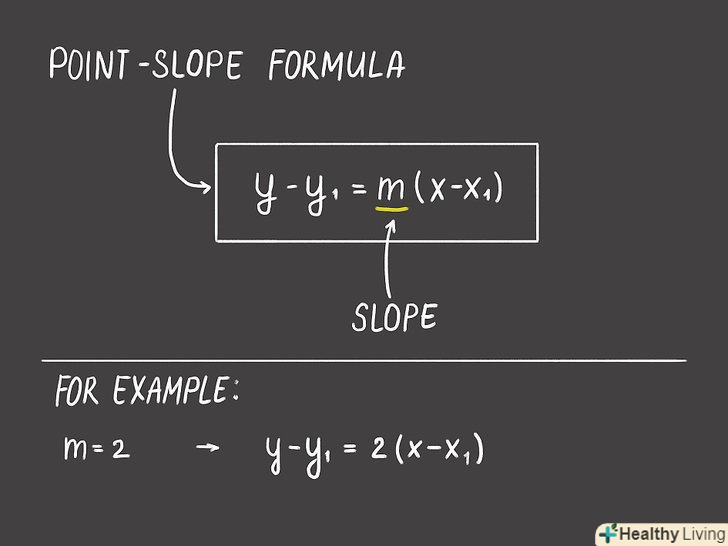
 Складіть довжини двох суміжних сторін і помножте отримане значення на 2.якщо W-ширина і H-висота, периметр прямокутника: P=2( w + h)
Складіть довжини двох суміжних сторін і помножте отримане значення на 2.якщо W-ширина і H-висота, периметр прямокутника: P=2( w + h)
Метод2З 6:
Квадрат
Метод2З 6:
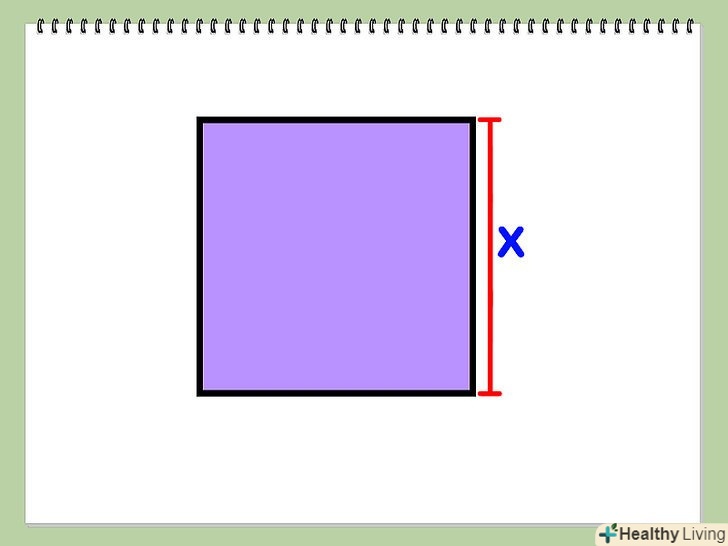
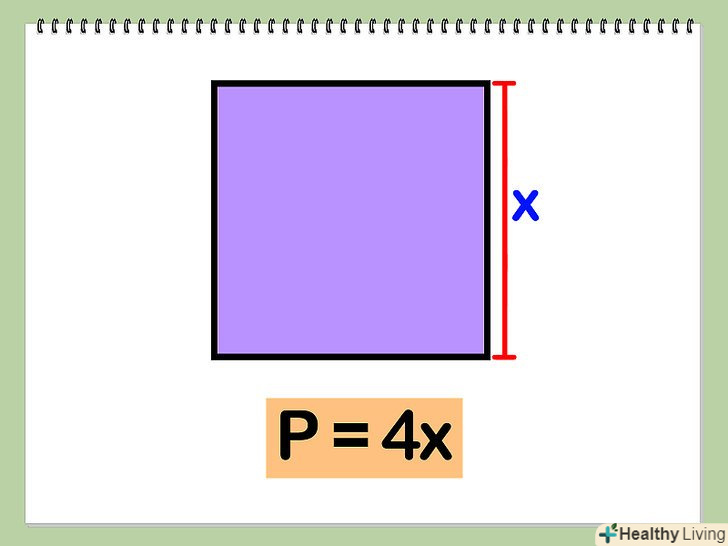
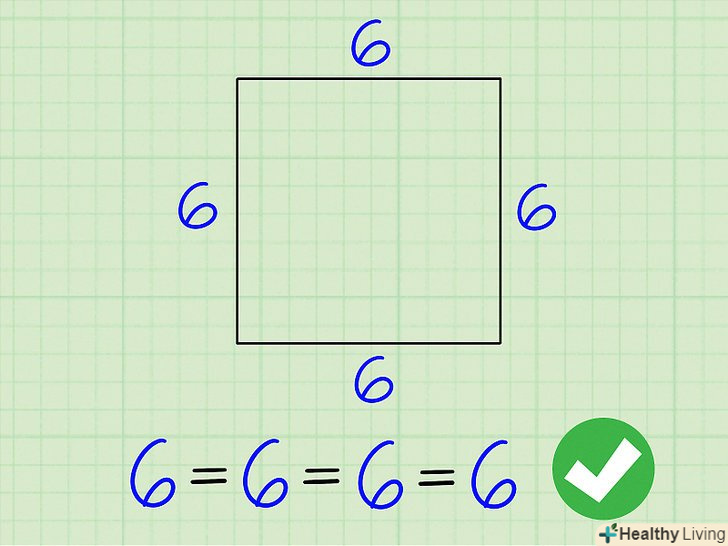
 Знайдіть довжину сторони квадрата (назвемо її х). Квадрат-фігура, у якій всі сторони рівні і присікаються під прямим кутом.
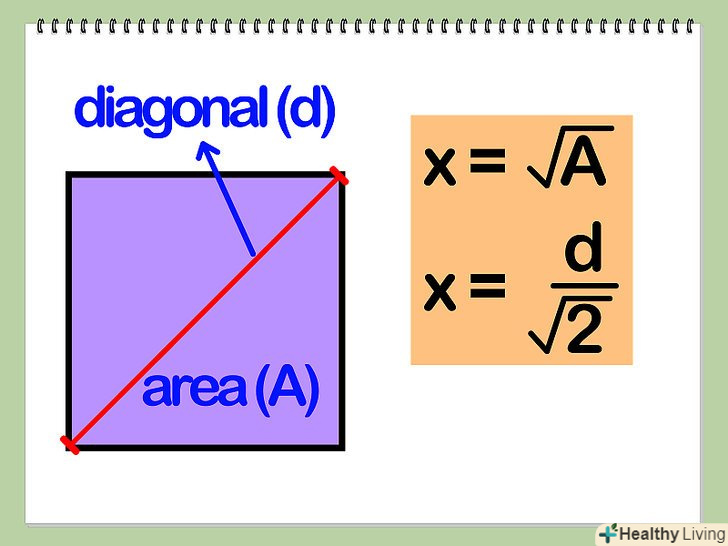
Знайдіть довжину сторони квадрата (назвемо її х). Квадрат-фігура, у якій всі сторони рівні і присікаються під прямим кутом. Якщо дана площа (A) квадрата, ви можете знайти довжину сторони, взявши квадратний корінь з площі: х = √ (A).
Якщо дана площа (A) квадрата, ви можете знайти довжину сторони, взявши квадратний корінь з площі: х = √ (A).- Якщо дана діагональ (d) квадрата, ви можете знайти довжину сторони, розділивши діагональ на квадратний корінь з 2: х = D/√2
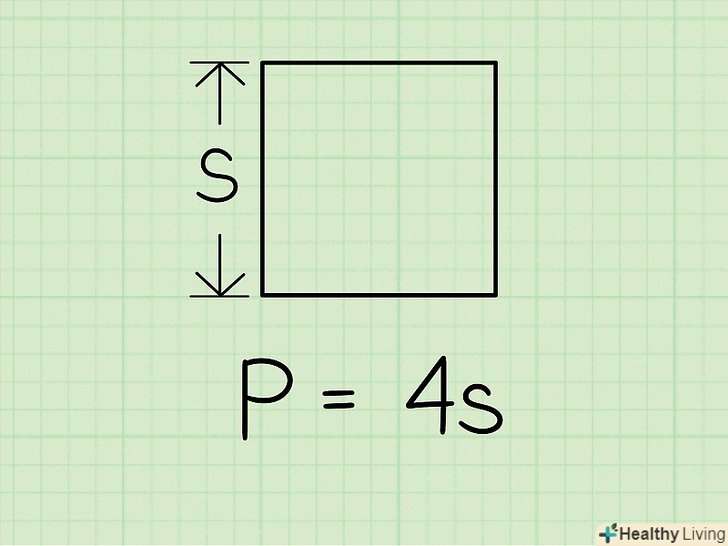
 Помножте довжину сторони на чотири.оскільки всі чотири сторони мають однакову довжину, периметр квадрата дорівнює учетверенной довжині однієї сторони: Р = 4x.
Помножте довжину сторони на чотири.оскільки всі чотири сторони мають однакову довжину, периметр квадрата дорівнює учетверенной довжині однієї сторони: Р = 4x.
Метод3З 6:
Коло
Метод3З 6:
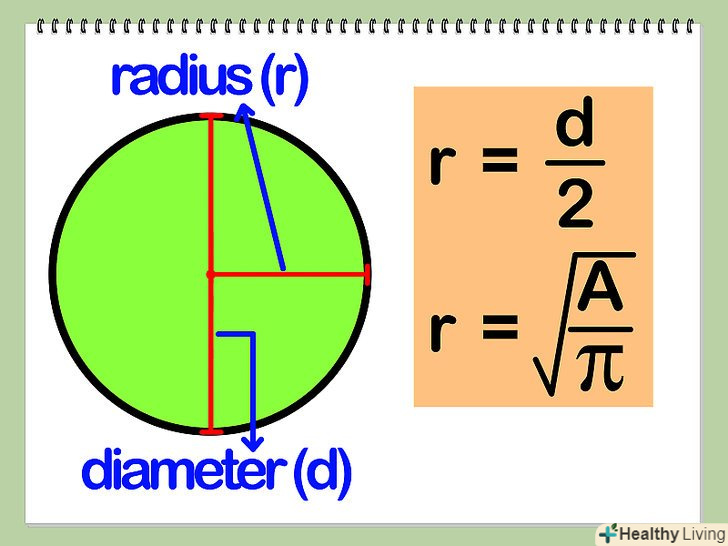
 Знайдіть довжину радіуса (r).радіус є відстанню від центру кола до будь-якої точки на окружності.
Знайдіть довжину радіуса (r).радіус є відстанню від центру кола до будь-якої точки на окружності.- Якщо дано діаметр (d) кола, ви можете знайти радіус, розділивши діаметр на два: г = D/2
- Якщо дано площу (A) кола, ви можете знайти радіус, розділивши площу на π, а потім взявши квадратний корінь з отриманого значення: г = √(A/π)
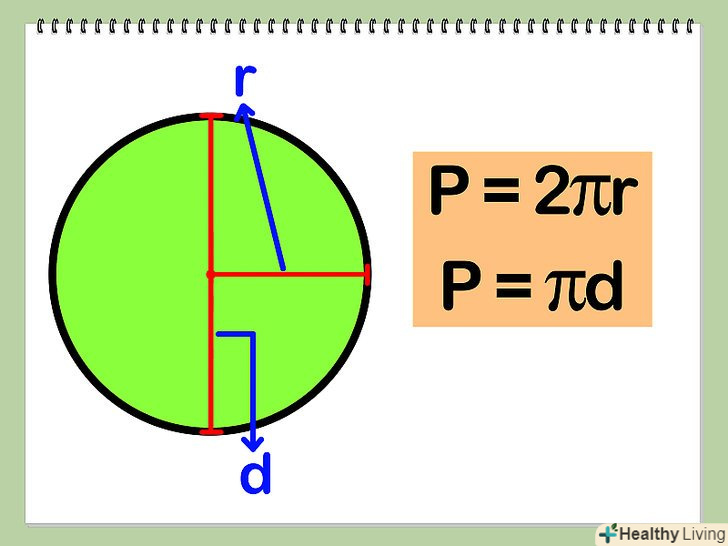
 Знайдіть периметр, помноживши радіус на 2π: Р = 2πR.
Знайдіть периметр, помноживши радіус на 2π: Р = 2πR.- Так як діаметр-це подвоєний радіус, периметр може бути знайдений за формулою: P = πd.
Метод4З 6:
Прямокутний трикутник
Метод4З 6:
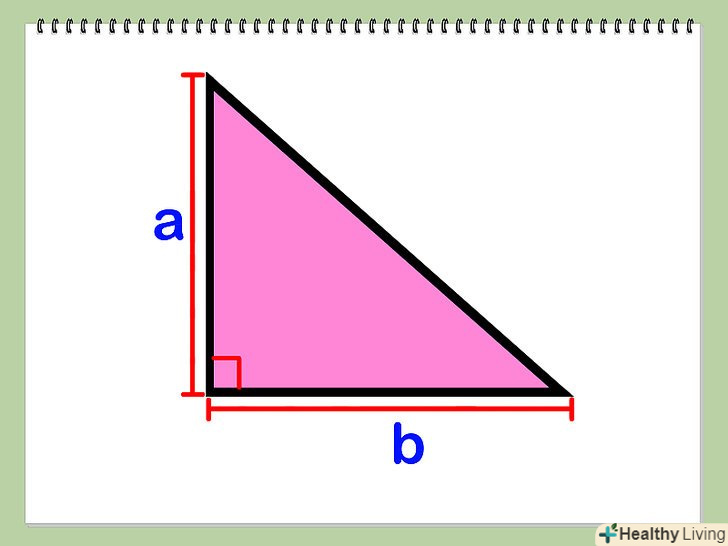
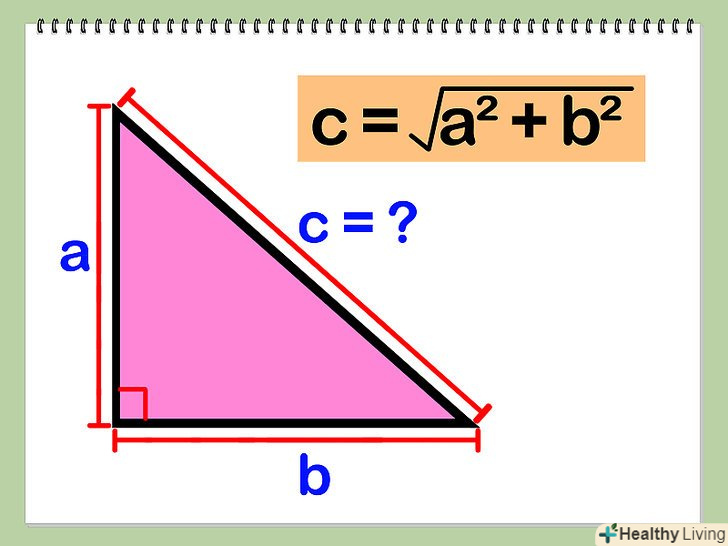
 Знайдіть довжини двох сторін трикутника (А і b), що перетинаються під прямим кутом.
Знайдіть довжини двох сторін трикутника (А і b), що перетинаються під прямим кутом. Знайдіть суму квадратів а і b, а потім витягніть квадратний корінь з отриманої суми: √(а^2 + b^2). За теоремою Піфагора, а^2 + b^2 = с^2, де с - довжина гіпотенузи, тобто сторони, що лежить навпроти прямого кута.
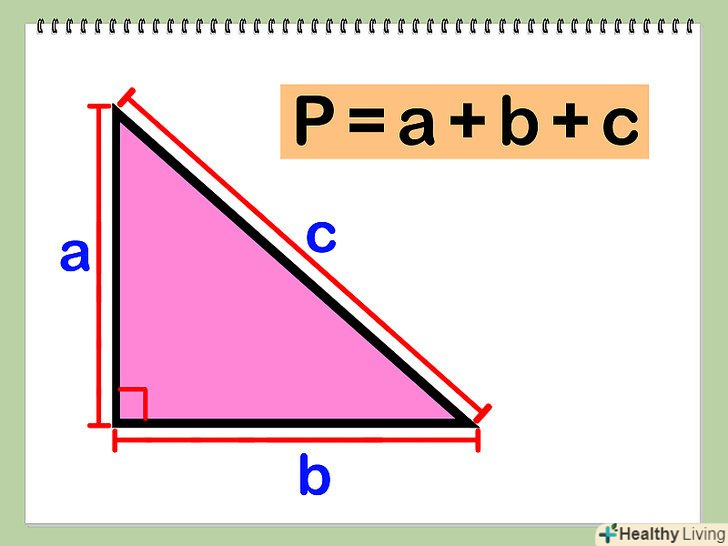
Знайдіть суму квадратів а і b, а потім витягніть квадратний корінь з отриманої суми: √(а^2 + b^2). За теоремою Піфагора, а^2 + b^2 = с^2, де с - довжина гіпотенузи, тобто сторони, що лежить навпроти прямого кута. Тепер, коли у вас є а, b і с (всі три сторони трикутника), просто складіть їх для знаходження периметра: P = а+b+с.
Тепер, коли у вас є а, b і с (всі три сторони трикутника), просто складіть їх для знаходження периметра: P = а+b+с.
Метод5З 6:
Трикутник
Метод5З 6:
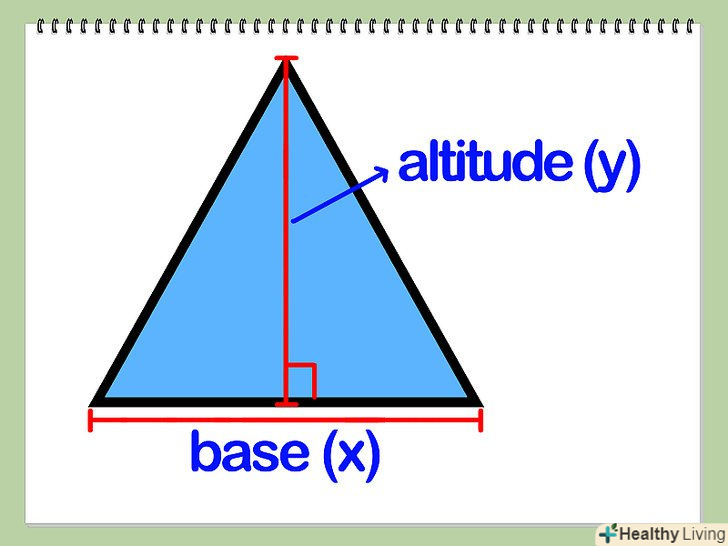
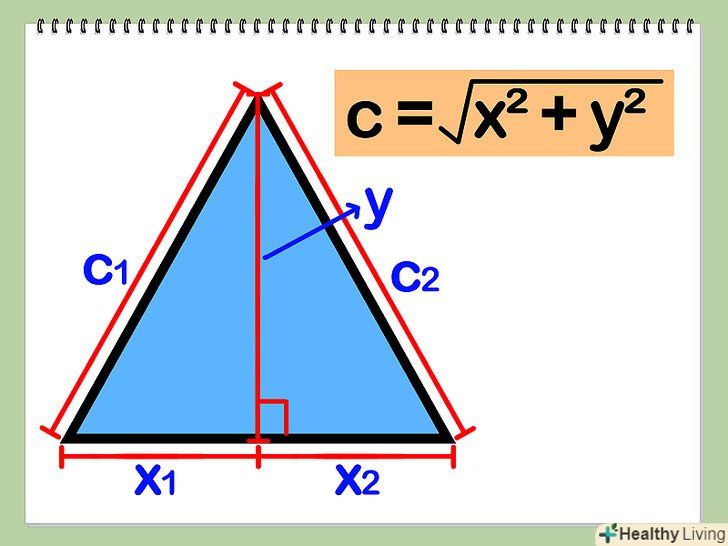
 Знайдіть висоту трикутника (у) і його підставу (х) (сторона, до якої проведений перпендикуляр – висота).
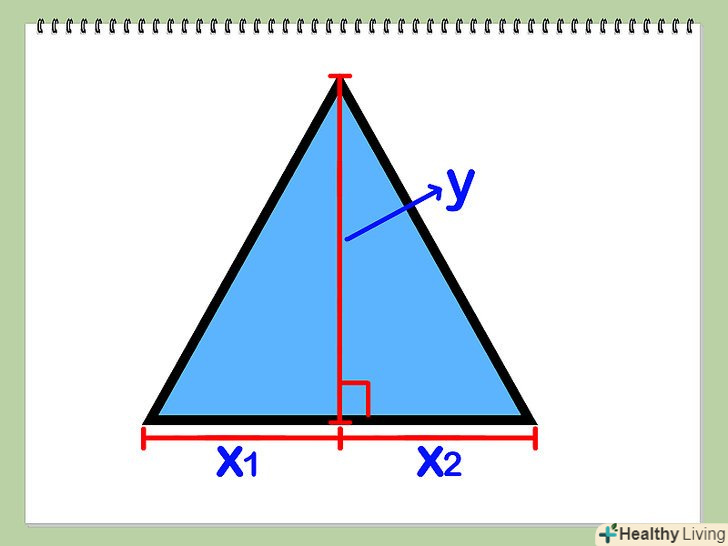
Знайдіть висоту трикутника (у) і його підставу (х) (сторона, до якої проведений перпендикуляр – висота). Знайдіть довжини відрізків х1 і х2, на які висота ділить підставу (тобто Х = х1 + х2). Висота ділить трикутник на два прямокутних трикутника (один з катетами х1 і у, інший з катетами х2 і у), і необхідно знайти довжини гіпотенуз цих трикутників с1 і с2.
Знайдіть довжини відрізків х1 і х2, на які висота ділить підставу (тобто Х = х1 + х2). Висота ділить трикутник на два прямокутних трикутника (один з катетами х1 і у, інший з катетами х2 і у), і необхідно знайти довжини гіпотенуз цих трикутників с1 і с2. Знайдіть с1 і с2.для цього використовуйте теорему Піфагора: а^2 + b^2 = с^2, і підставте x1 замість a, y замість b, c1 замість C. повторіть для х2, у, і с2.
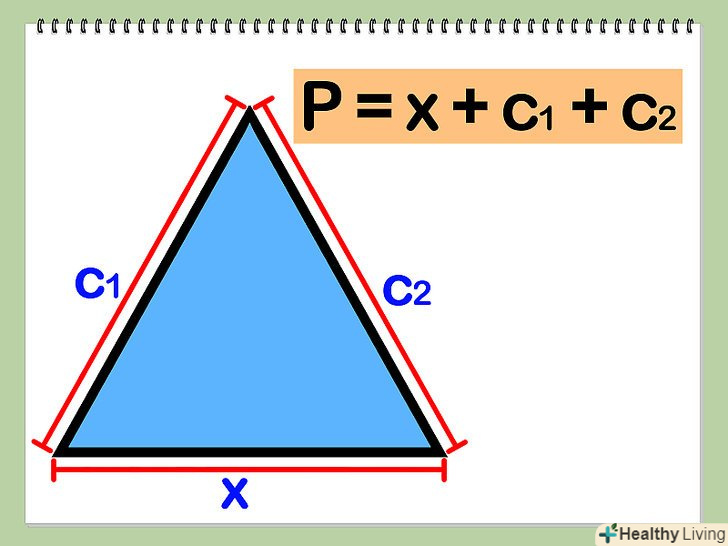
Знайдіть с1 і с2.для цього використовуйте теорему Піфагора: а^2 + b^2 = с^2, і підставте x1 замість a, y замість b, c1 замість C. повторіть для х2, у, і с2. Складіть х, с1 і с2, які є трьома сторонами вихідного трикутника.
Складіть х, с1 і с2, які є трьома сторонами вихідного трикутника.
Метод6З 6:
Правильний багатокутник
Метод6З 6:
 Знайдіть довжину однієї сторони правильного багатокутника. за визначенням, правильний багатокутник-це фігура з рівними сторонами і кутами.
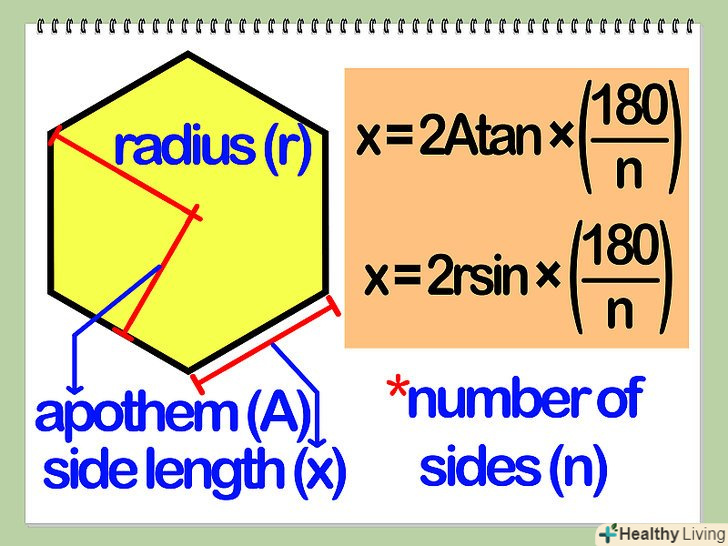
Знайдіть довжину однієї сторони правильного багатокутника. за визначенням, правильний багатокутник-це фігура з рівними сторонами і кутами.- Якщо дана апофема (перпендикуляр, опущений з центру багатокутника до однієї з його сторін), Ви можете знайти довжину сторони. Якщо n-число сторін багатокутника, а-довжина апофеми, довжина сторони: x=2(180/n).
- Якщо дано радіус (відстань між центром і будь-якою вершиною), ви можете знайти довжину сторони: x=2rsin(180/n), де r – радіус, n – число сторін багатокутника.
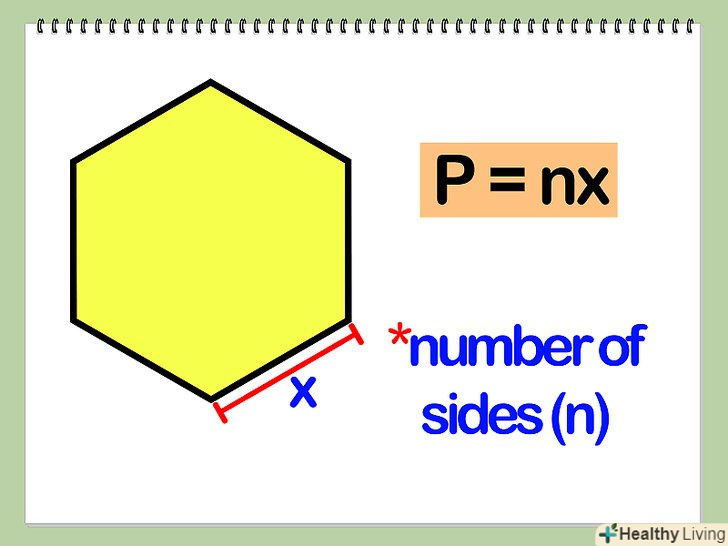
 Помножте довжину однієї сторони багатокутника на число його сторін.таким чином, P=nx, де n – число сторін багатокутника, х – довжина однієї сторони багатокутника.
Помножте довжину однієї сторони багатокутника на число його сторін.таким чином, P=nx, де n – число сторін багатокутника, х – довжина однієї сторони багатокутника.