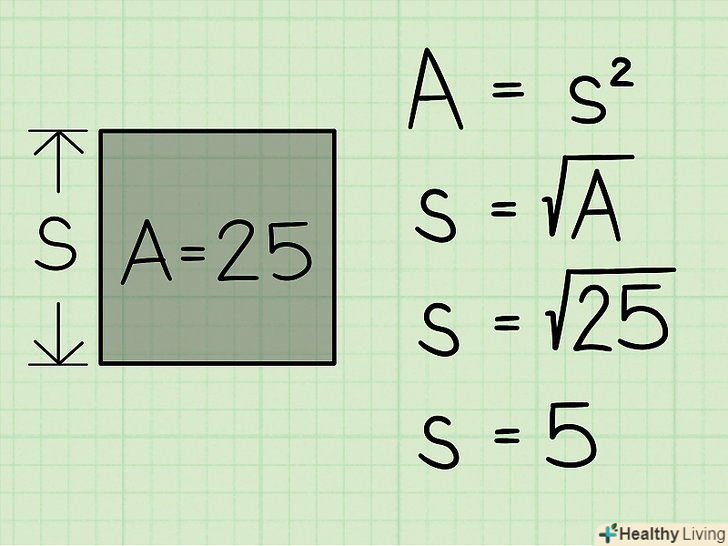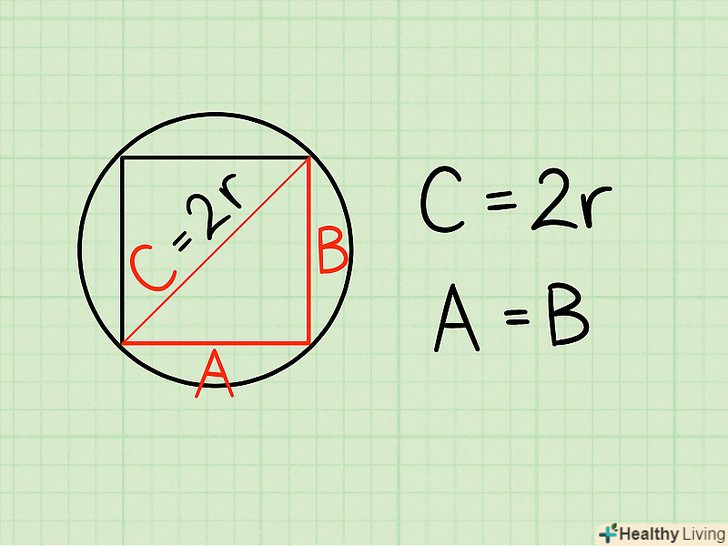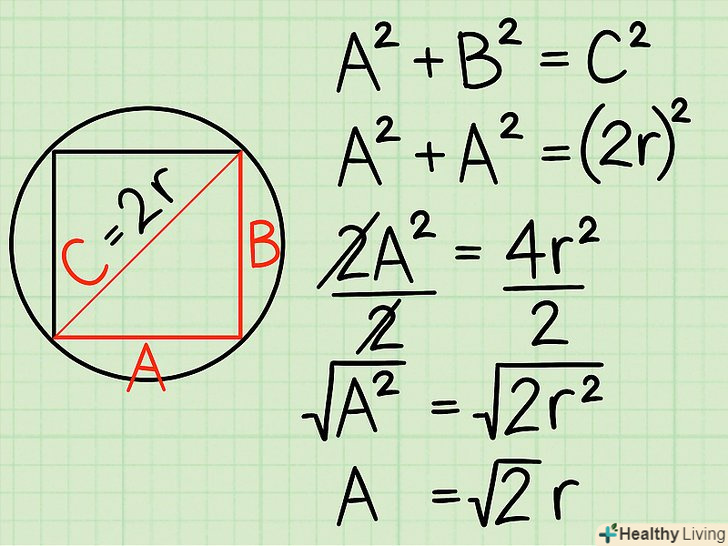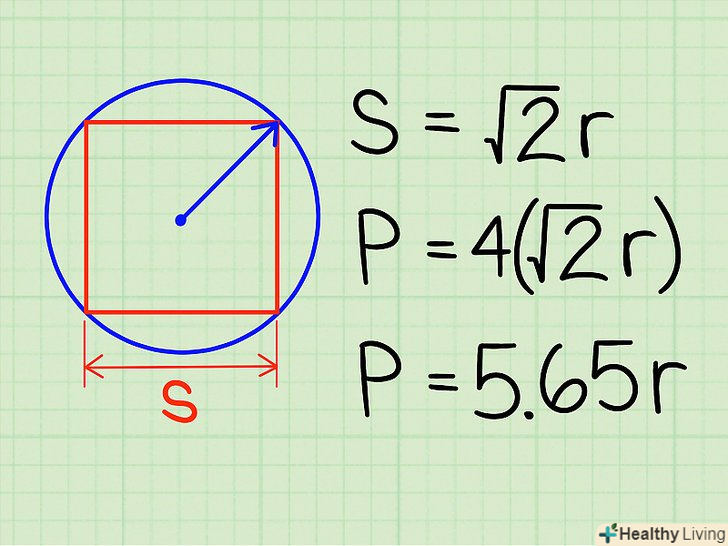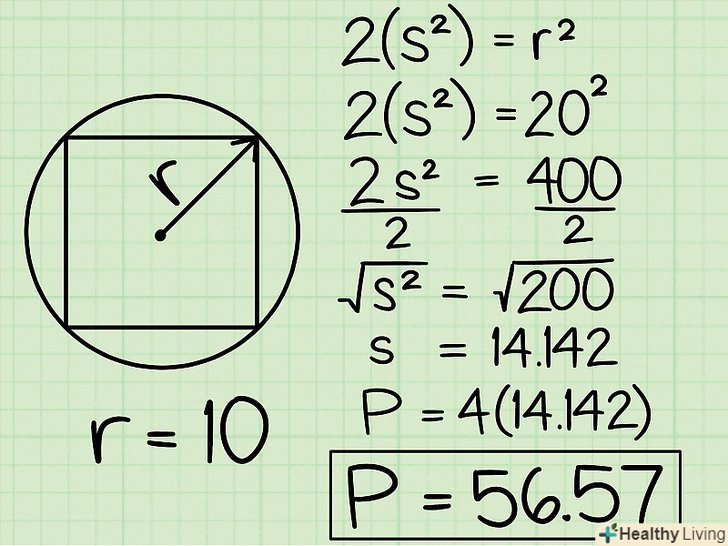Периметр двовимірної фігури-це загальна довжина її кордону, рівна сумі довжин сторін фігури.[1] Квадрат-це фігура з чотирма сторонами однакової довжини, які перетинаються під кутом 90°.[2] Так як в квадраті всі сторони мають однакову довжину, то обчислити його периметр дуже легко. Ця стаття розповість вам, як обчислити периметр квадрата по одній даній стороні, по даній площі і по даному радіусу кола, описаної навколо квадрата.
Кроки
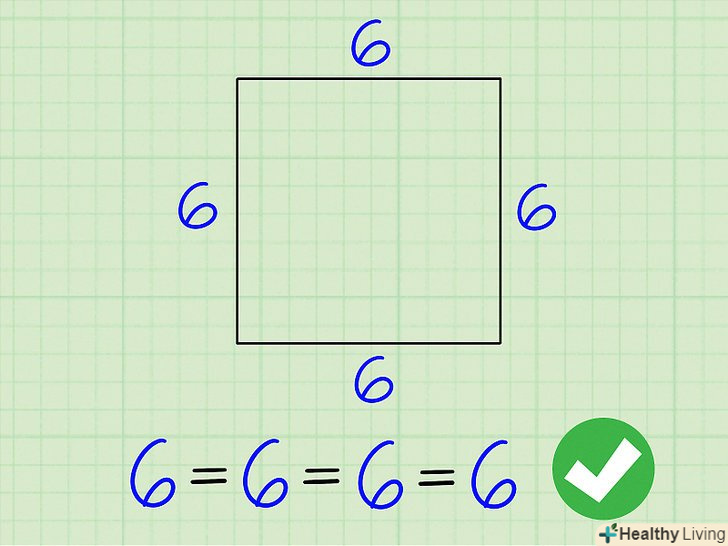
Метод1З 3:
Обчислення периметра по даній стороні
Метод1З 3:
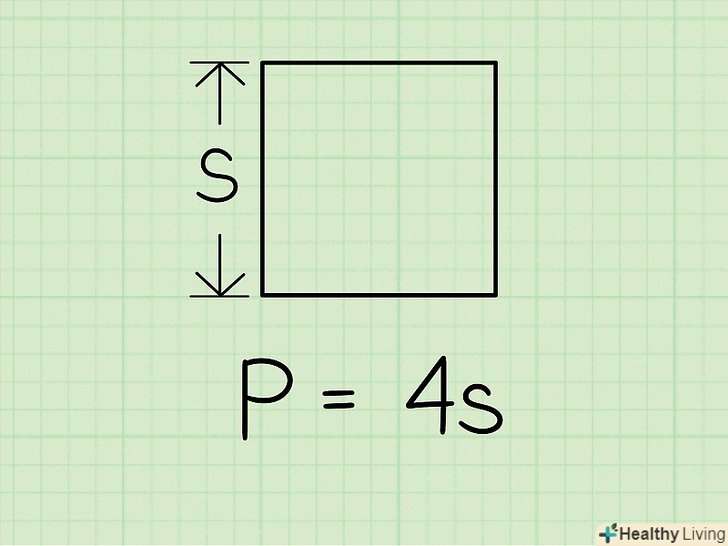
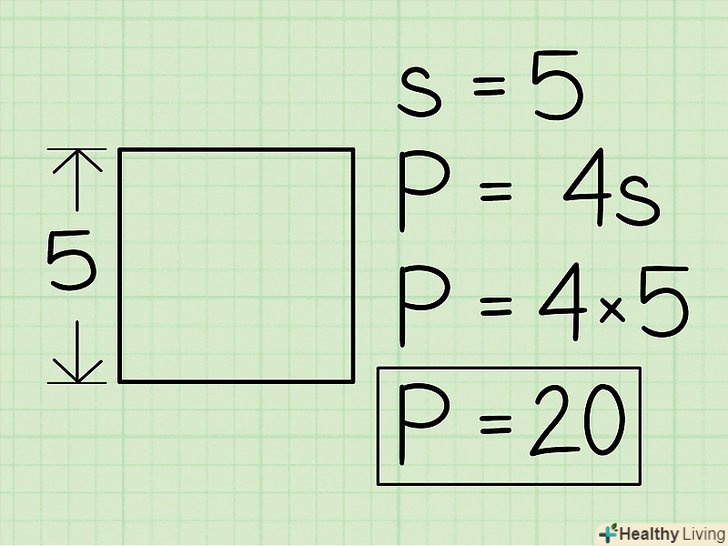
 Формула для обчислення периметра квадрата:P = 4S, деS – довжина сторони квадрата.
Формула для обчислення периметра квадрата:P = 4S, деS – довжина сторони квадрата. Визначте довжину однієї сторони квадрата і помножте її на 4, щоб знайти периметр. щоб визначити довжину сторони, виміряйте її лінійкою або подивіться її значення в підручнику (задачі). Ось деякі приклади обчислення периметра:
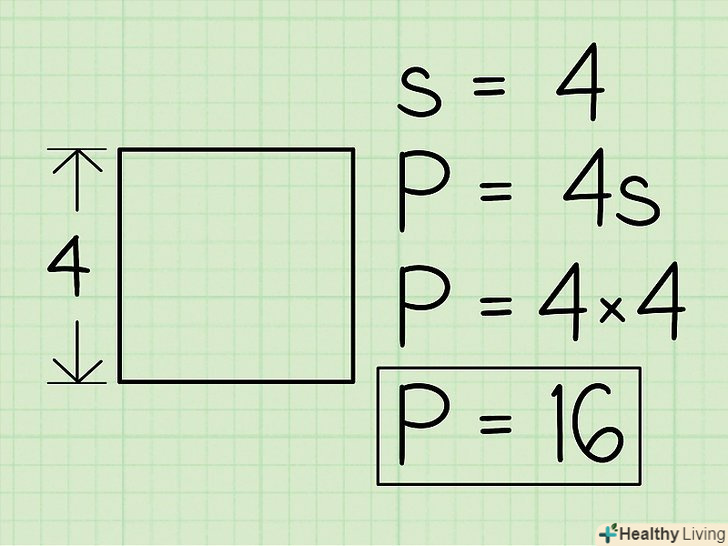
Визначте довжину однієї сторони квадрата і помножте її на 4, щоб знайти периметр. щоб визначити довжину сторони, виміряйте її лінійкою або подивіться її значення в підручнику (задачі). Ось деякі приклади обчислення периметра:- Якщо сторона квадрата дорівнює 4, тоP = 4 * 4 = 16.
- Якщо сторона квадрата дорівнює 6, тоP = 4 * 6 = 36.
Метод2 З 3:
Обчислення периметра по даній площі
Метод2 З 3:
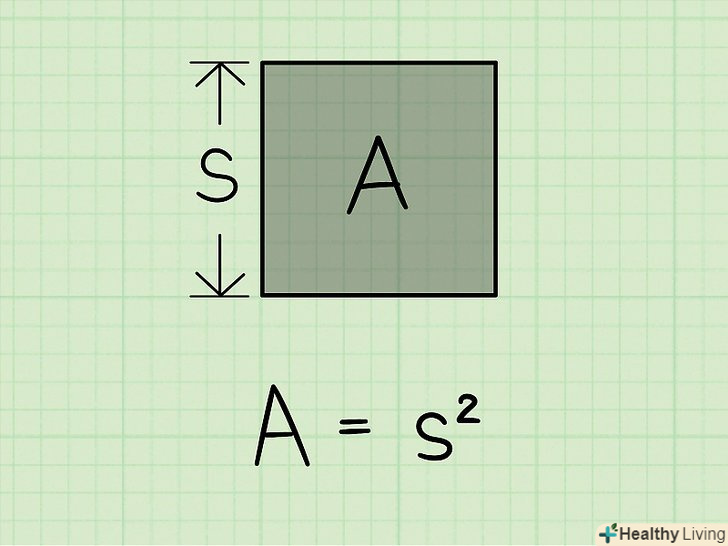
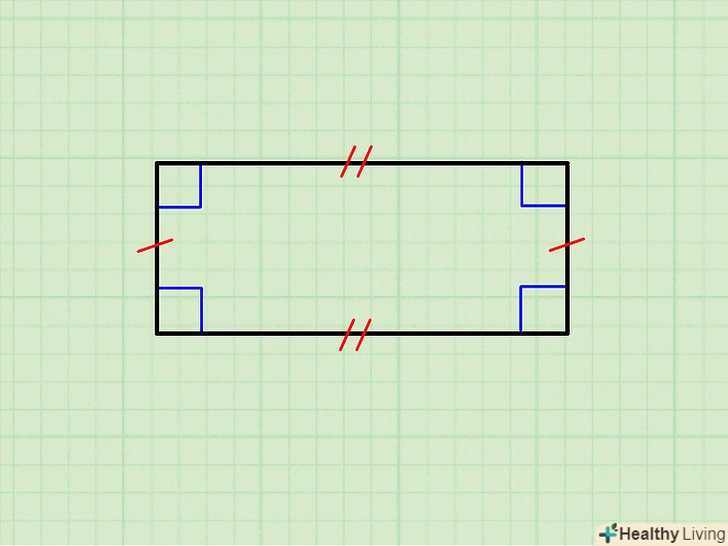
 Формула для обчислення площі квадрата. Площа будь-якого прямокутника (а квадрат – це окремий випадок прямокутника) дорівнює добутку його довжини на його ширину.[3] оскільки довжина і ширина квадрата рівні, то його площа обчислюється за формулою: A = s * S = s2, де S – довжина сторони квадрата.
Формула для обчислення площі квадрата. Площа будь-якого прямокутника (а квадрат – це окремий випадок прямокутника) дорівнює добутку його довжини на його ширину.[3] оскільки довжина і ширина квадрата рівні, то його площа обчислюється за формулою: A = s * S = s2, де S – довжина сторони квадрата. Витягніть квадратний корінь із значення площі, щоб знайти сторону квадрата.для цього в більшості випадків скористайтеся калькулятором (введіть значення площі і натисніть клавішу"√"). Ви також можете обчислити квадратний корінь вручну.
Витягніть квадратний корінь із значення площі, щоб знайти сторону квадрата.для цього в більшості випадків скористайтеся калькулятором (введіть значення площі і натисніть клавішу"√"). Ви також можете обчислити квадратний корінь вручну.- Якщо площа квадрата дорівнює 20, то його сторона дорівнює:S = √20 = 4,472.
- Якщо площа квадрата дорівнює 25, тоS = √25 = 5.
 Помножте знайдену сторону на 4, щоб знайти периметр. обчислене значення сторони підставте в формулу для знаходження периметра:P = 4S. Ви знайдете периметр квадрата.
Помножте знайдену сторону на 4, щоб знайти периметр. обчислене значення сторони підставте в формулу для знаходження периметра:P = 4S. Ви знайдете периметр квадрата.- У нашому першому прикладі:P = 4 * 4,472 = 17,888.
- Периметр квадрата, площа якого дорівнює 25, а сторона дорівнює 5, дорівнюєР = 4 * 5 = 20.
Метод3 З 3:
Обчислення периметра з даного радіуса кола, описаної навколо квадрата
Метод3 З 3:
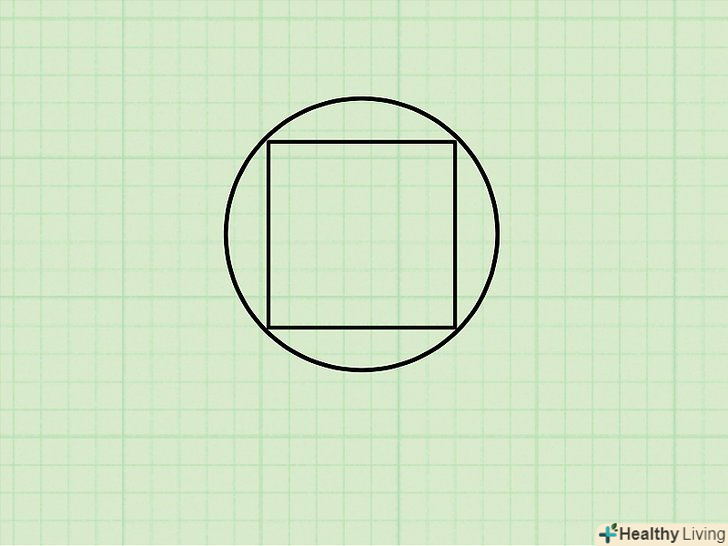
 Вписаний квадрат-це квадрат, вершини якого лежать на окружності.[4]
Вписаний квадрат-це квадрат, вершини якого лежать на окружності.[4] Відношення між радіусом кола і довжиною сторони квадрата.відстань від центру описаного кола до вершини вписаного в неї квадрата дорівнює радіусу кола. Щоб знайти сторону квадрата ,необхідно діагоналлю розділити квадрат на 2 прямокутних трикутника. Кожен з цих трикутників матиме рівні сторони A іB і загальну гіпотенузуЗ, рівну подвоєному радіусу описаного кола (2r).
Відношення між радіусом кола і довжиною сторони квадрата.відстань від центру описаного кола до вершини вписаного в неї квадрата дорівнює радіусу кола. Щоб знайти сторону квадрата ,необхідно діагоналлю розділити квадрат на 2 прямокутних трикутника. Кожен з цих трикутників матиме рівні сторони A іB і загальну гіпотенузуЗ, рівну подвоєному радіусу описаного кола (2r). Скористайтеся теоремою Піфагора, щоб знайти сторону квадрата. Теорема Піфагора говорить, що в будь-якому прямокутному трикутнику з катетамиА іB і гіпотенузоюЗ:A2 + b2 = c2 .[5] Так як в нашому випадкуА = B (Не забувайте, що ми розглядаємо квадрат!), і ми знаємо, що З = 2r, то ми можемо переписати і спростити це рівняння:
Скористайтеся теоремою Піфагора, щоб знайти сторону квадрата. Теорема Піфагора говорить, що в будь-якому прямокутному трикутнику з катетамиА іB і гіпотенузоюЗ:A2 + b2 = c2 .[5] Так як в нашому випадкуА = B (Не забувайте, що ми розглядаємо квадрат!), і ми знаємо, що З = 2r, то ми можемо переписати і спростити це рівняння:- A2 + a2 = (2R)2"'; тепер спростимо це рівняння:
- 2a2 = 4 (r)2; Тепер розділимо обидві сторони рівняння на 2:
- (a2) = 2 (r)2; Тепер витягнемо квадратний корінь з обох сторін рівняння:
- A = √(2r). Таким чином, s = √(2r).
 Помножте знайдену сторону квадрата на 4, щоб знайти його периметр.у цьому випадку периметр квадрата: P = 4√(2r). Цю формулу можна переписати так: Р = 4√2 * 4√r = 5,657 r, де r – радіус описаного кола.[6]
Помножте знайдену сторону квадрата на 4, щоб знайти його периметр.у цьому випадку периметр квадрата: P = 4√(2r). Цю формулу можна переписати так: Р = 4√2 * 4√r = 5,657 r, де r – радіус описаного кола.[6] Приклад.розглянемо квадрат, вписаний в коло радіусом 10. Це означає, що діагональ квадрата дорівнює 2 * 10 = 20. Використовуючи теорему Піфагора, ми отримаємо: 2 (a 2) = 202, тобто 2a 2 = 400. Тепер розділимо обидві сторони рівняння на 2 і отримаємо: A2 = 200.тепер витягнемо квадратний корінь з обох сторін рівняння і отримаємо: А = 14,142. Помножимо це значення на 4 і обчислимо периметр квадрата: P = 56,57.
Приклад.розглянемо квадрат, вписаний в коло радіусом 10. Це означає, що діагональ квадрата дорівнює 2 * 10 = 20. Використовуючи теорему Піфагора, ми отримаємо: 2 (a 2) = 202, тобто 2a 2 = 400. Тепер розділимо обидві сторони рівняння на 2 і отримаємо: A2 = 200.тепер витягнемо квадратний корінь з обох сторін рівняння і отримаємо: А = 14,142. Помножимо це значення на 4 і обчислимо периметр квадрата: P = 56,57.- Зверніть увагу, що Ви могли б отримати той же результат, просто помноживши радіус (10) на 5,657:10 * 5,567 = 56,57; але такий метод важко запам'ятати, тому краще користуватися процесом обчислення, описаним вище.
Джерела
- ↑ https://www.mathsisfun.com/definitions/perimeter.html
- ↑ Http://www.merriam-webster.com/dictionary/square
- ↑ Http://www.math.com/tables/geometry/areas.htm
- ↑ Http://www.mathopenref.com/squareinscribed.html
- ↑ Http://www.mathsisfun.com/pythagoras.html
- ↑ Http://mathinsight.org/exponentiation_basic_rules