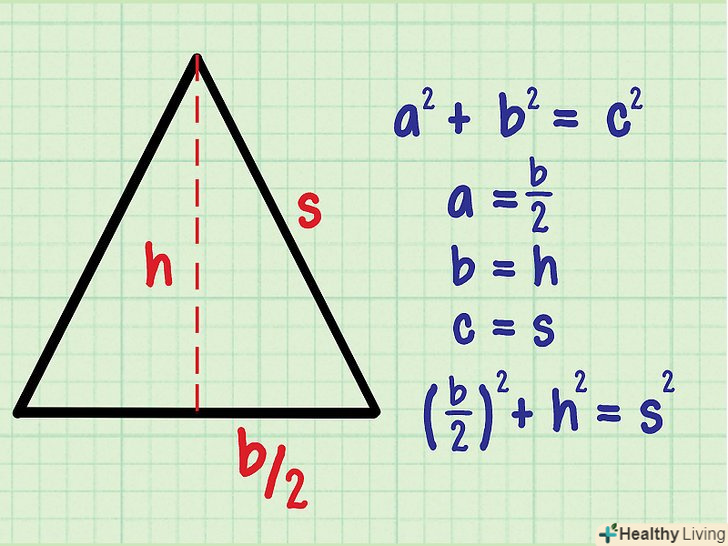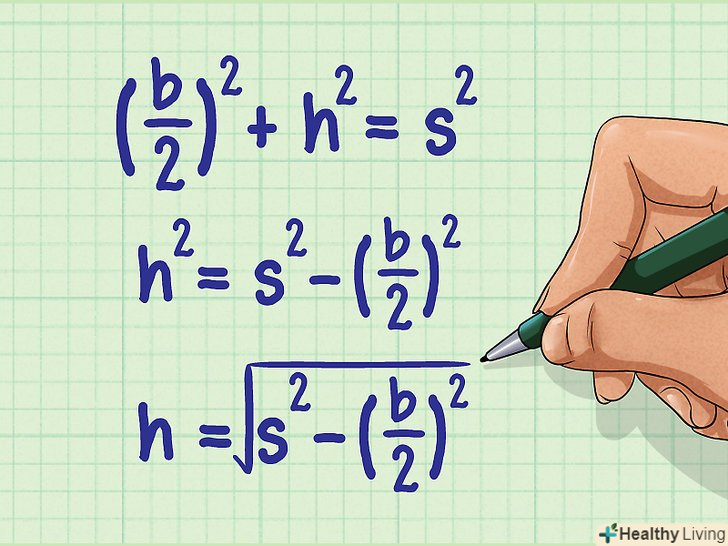Рівнобедрений трикутник-це трикутник, у якого дві сторони рівні. Рівні (бічні) сторони перетинають третю сторону (підстава) під одним кутом, а точка перетину рівних сторін знаходиться над серединою підстави. У цьому можна переконатися за допомогою лінійки і двох олівців однакової довжини: якщо нахилити трикутник в одну або іншу сторону, кінчики олівців не з'єднаються. Такі властивості рівнобедреного трикутника дозволяють обчислити його площа всього лише за кількома відомим величинам.
Кроки
Метод1 З 2:
Як обчислити площу по бічних сторонах
Метод1 З 2:
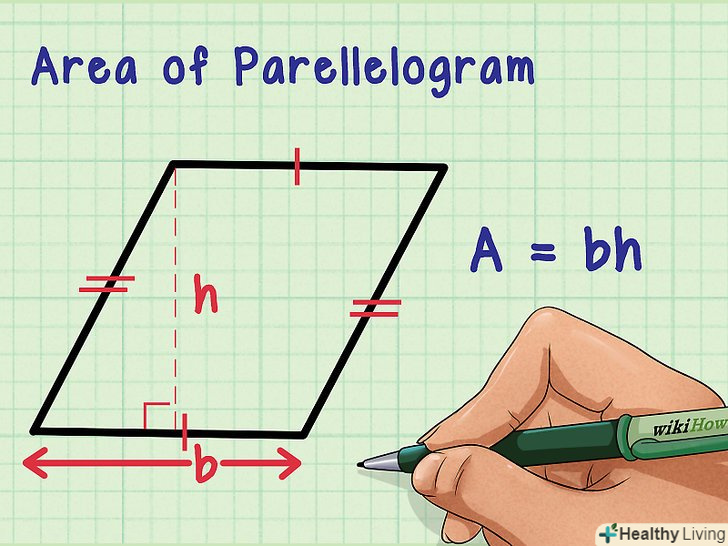
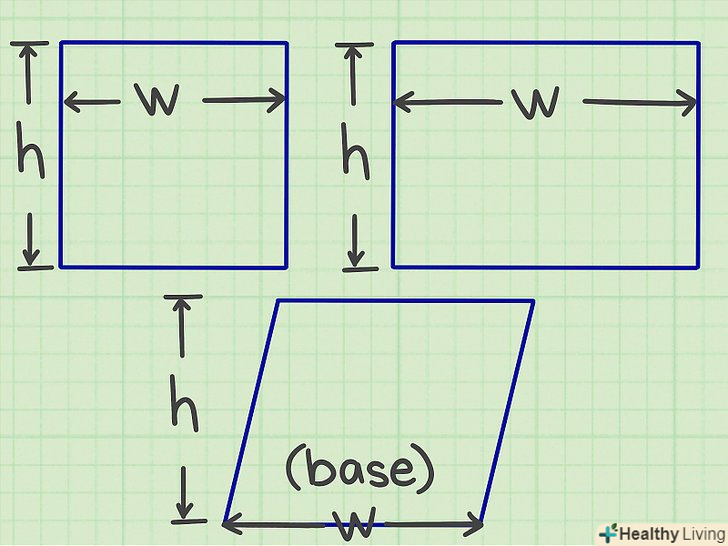
 З'ясуйте, як знайти площу паралелограма.квадрати і прямокутники є паралелограмами, як і будь-яка інша чотиристороння фігура, у якій протилежні сторони паралельні. Площа паралелограма обчислюється за формулою: S = BH,[1] де «b» – підстава (нижня сторона паралелограма), «h» – висота (відстань від верхньої до нижньої сторони; висота завжди перетинає підставу під кутом 90°).
З'ясуйте, як знайти площу паралелограма.квадрати і прямокутники є паралелограмами, як і будь-яка інша чотиристороння фігура, у якій протилежні сторони паралельні. Площа паралелограма обчислюється за формулою: S = BH,[1] де «b» – підстава (нижня сторона паралелограма), «h» – висота (відстань від верхньої до нижньої сторони; висота завжди перетинає підставу під кутом 90°).- У квадратах і прямокутниках висота дорівнює бічній стороні, так як бічні сторони перетинають верхню і нижню сторони під прямим кутом.
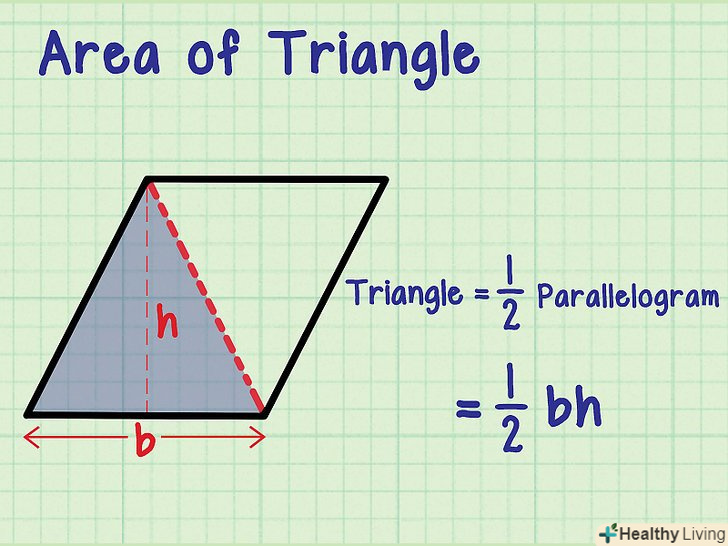
 Порівняйте трикутники і паралелограми. Між цими фігурами існує проста зв'язок. Якщо будь-який паралелограм розрізати по діагоналі, вийдуть два рівних трикутника. Аналогічно, якщо скласти два рівних трикутника, вийде паралелограм. Тому Площа будь-якого трикутника обчислюється за формулою: S =½, що становить половину площі паралелограма.
Порівняйте трикутники і паралелограми. Між цими фігурами існує проста зв'язок. Якщо будь-який паралелограм розрізати по діагоналі, вийдуть два рівних трикутника. Аналогічно, якщо скласти два рівних трикутника, вийде паралелограм. Тому Площа будь-якого трикутника обчислюється за формулою: S =½, що становить половину площі паралелограма. Знайдіть основу рівнобедреного трикутника.тепер ви знаєте формулу для обчислення площі трикутника; залишилося з'ясувати, що таке «підстава» і «висота». Підстава (позначається як «b») – Це сторона, яка не дорівнює двом іншим (рівним) сторонам.
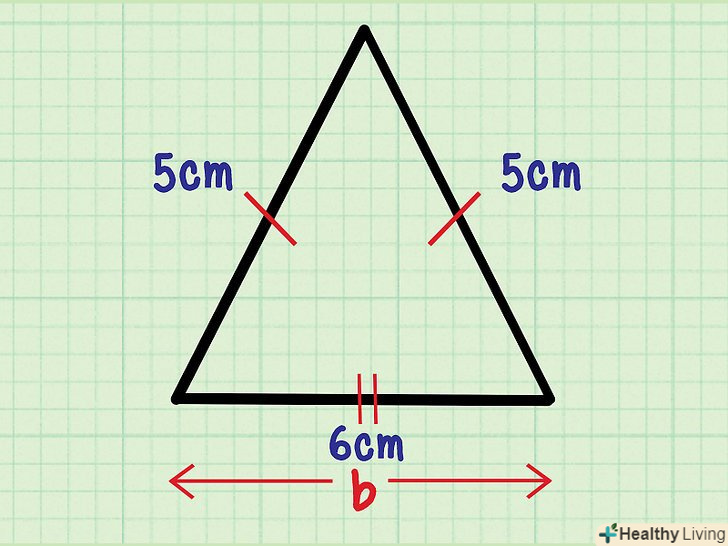
Знайдіть основу рівнобедреного трикутника.тепер ви знаєте формулу для обчислення площі трикутника; залишилося з'ясувати, що таке «підстава» і «висота». Підстава (позначається як «b») – Це сторона, яка не дорівнює двом іншим (рівним) сторонам.- Наприклад, якщо сторони рівнобедреного трикутника рівні 5 см, 5 см, 6 см, в якості підстави виберіть сторону, яка дорівнює 6 см.
- Якщо всі сторони трикутника рівні (рівносторонній трикутник), в якості підстави Виберіть будь-яку сторону. Рівносторонній трикутник є окремим випадком рівнобедреного трикутника, але його площа обчислюється так само.[2]
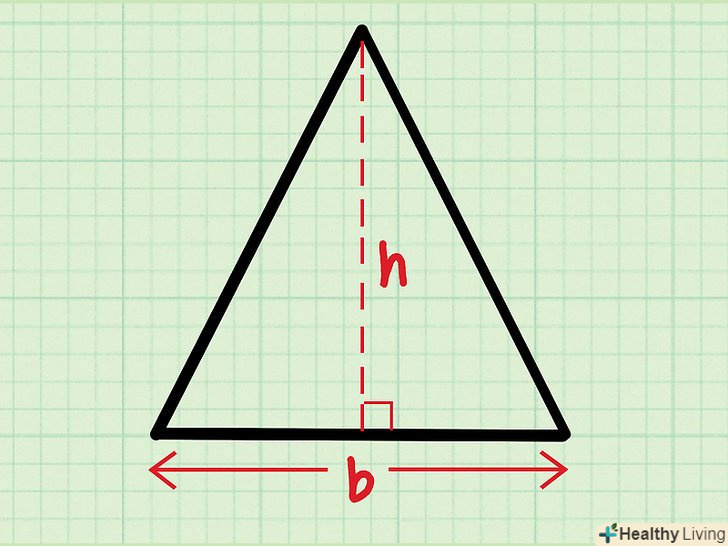
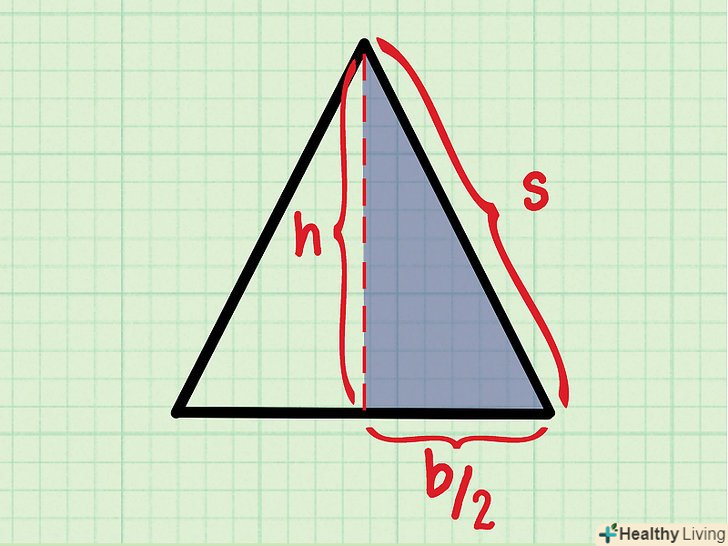
 Опустіть перпендикуляр на підставу.зробіть це з вершини трикутника, Яка протилежна підставі. Пам'ятайте, що перпендикуляр перетинає підставу під прямим кутом. Такий перпендикуляр є висотою трикутника (позначається як «h»). Як тільки ви знайдете значення "h", ви зможете обчислити площу трикутника.
Опустіть перпендикуляр на підставу.зробіть це з вершини трикутника, Яка протилежна підставі. Пам'ятайте, що перпендикуляр перетинає підставу під прямим кутом. Такий перпендикуляр є висотою трикутника (позначається як «h»). Як тільки ви знайдете значення "h", ви зможете обчислити площу трикутника.- У рівнобедреному трикутнику висота перетинає підставу точно посередині.
 Подивіться на половину рівнобедреного трикутника.зверніть увагу, що висота розділила рівнобедрений трикутник на два рівних прямокутних трикутника. Подивіться на один з них і знайдіть його сторони:
Подивіться на половину рівнобедреного трикутника.зверніть увагу, що висота розділила рівнобедрений трикутник на два рівних прямокутних трикутника. Подивіться на один з них і знайдіть його сторони:- Коротка сторона дорівнює половині підстави:
.
- Друга сторона-це висота "h".
- Гіпотенуза прямокутного трикутника є бічною стороною рівнобедреного трикутника; позначимо її як «s».
- Коротка сторона дорівнює половині підстави:
 Скористайтеся теоремою Піфагора . якщо відомі дві сторони прямокутного трикутника, його третю сторону можна обчислити за теоремою Піфагора: (сторона 1)2 + (сторона 2)2 = (гіпотенуза)2. У нашому прикладі теорема Піфагора запишеться так:
Скористайтеся теоремою Піфагора . якщо відомі дві сторони прямокутного трикутника, його третю сторону можна обчислити за теоремою Піфагора: (сторона 1)2 + (сторона 2)2 = (гіпотенуза)2. У нашому прикладі теорема Піфагора запишеться так:.
- Швидше за все, теорема Піфагора вам відома в такому записі:
. Ми вживаємо слова "сторона 1», «сторона 2» і "гіпотенуза", щоб запобігти плутанині зі змінними з прикладу.
- Швидше за все, теорема Піфагора вам відома в такому записі:
 Обчисліть значення "h".Пам'ятайте, що у формулі для обчислення площі трикутника є змінні " b " і "h", але значення «h» невідомо. Перепишіть формулу, щоб обчислити " h»:
Обчисліть значення "h".Пам'ятайте, що у формулі для обчислення площі трикутника є змінні " b " і "h", але значення «h» невідомо. Перепишіть формулу, щоб обчислити " h»:.

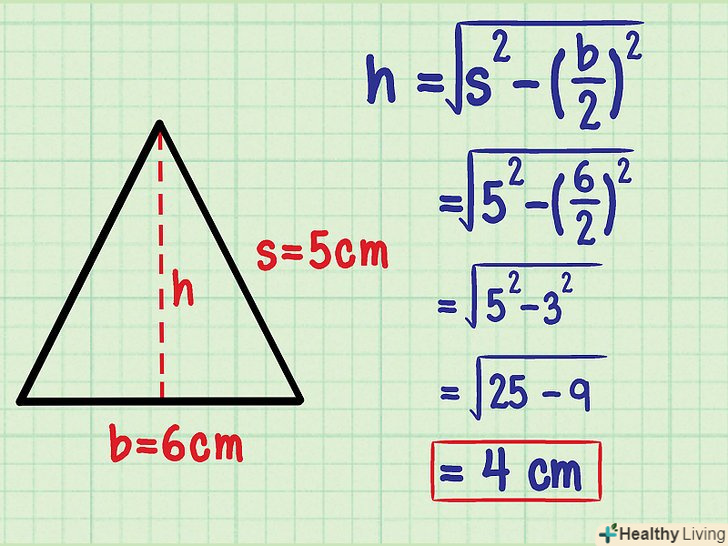
- У нашому прикладі: b = 6 см; s = 5 см.
- Підставте значення у формулу:
див.
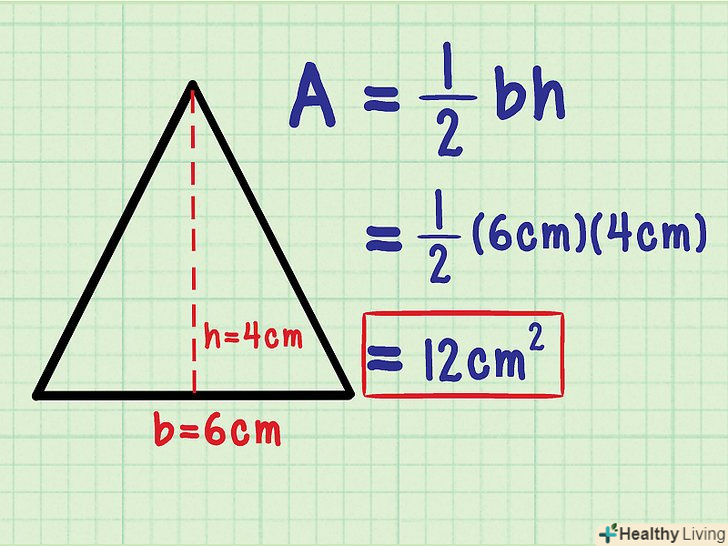
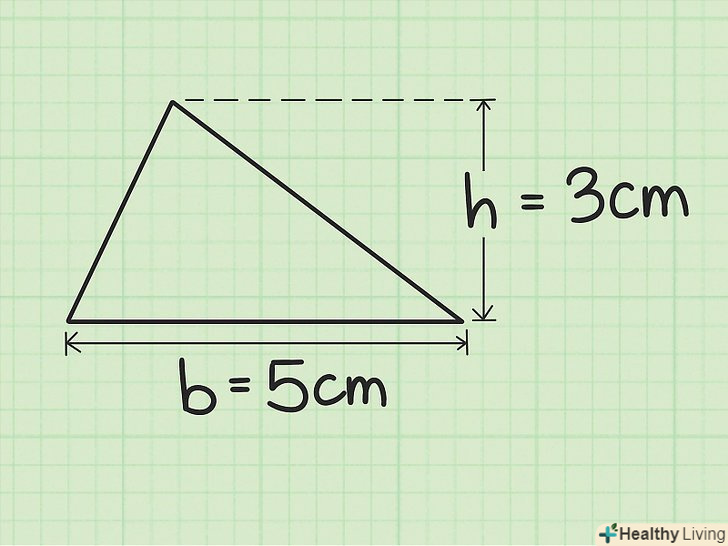
 Підставте значення підстави і висоти в формулу для обчислення площі трикутника. Формула: S = ½bh; підставте в неї значення» b «і» h " і обчисліть площу. У відповіді не забудьте написати квадратні одиниці виміру.
Підставте значення підстави і висоти в формулу для обчислення площі трикутника. Формула: S = ½bh; підставте в неї значення» b «і» h " і обчисліть площу. У відповіді не забудьте написати квадратні одиниці виміру.- У нашому прикладі підстава дорівнює 6 см, а висота дорівнює 4 см.
- S = ½bh
s = ½(6 см)(4 см)
S = 12 см2.
 Розглянемо більш складний приклад.у більшості випадків вам буде дана більш важке завдання, ніж розглянута в нашому прикладі. Щоб обчислити висоту, потрібно витягти квадратний корінь, який, як правило, не витягується. У цьому випадку запишіть значення висоти у вигляді спрощеного квадратного кореня. Ось новий приклад:
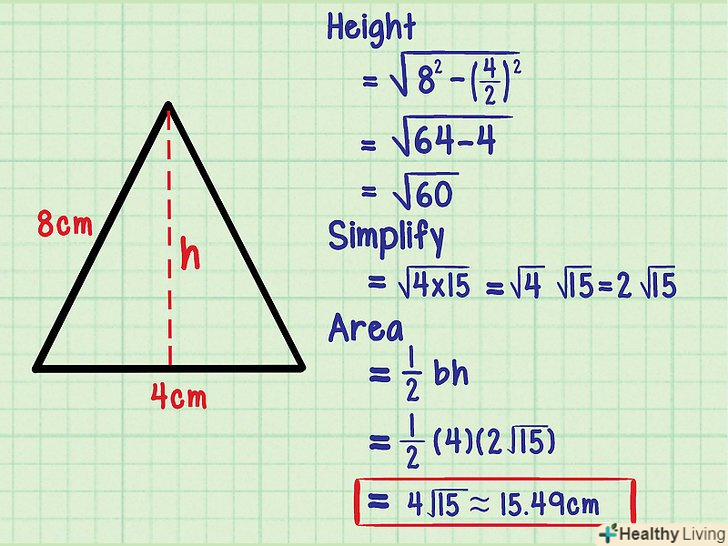
Розглянемо більш складний приклад.у більшості випадків вам буде дана більш важке завдання, ніж розглянута в нашому прикладі. Щоб обчислити висоту, потрібно витягти квадратний корінь, який, як правило, не витягується. У цьому випадку запишіть значення висоти у вигляді спрощеного квадратного кореня. Ось новий приклад:- Обчисліть площу рівнобедреного трикутника, сторони якого рівні 8 см, 8 см, 4 см.
- В якості підстави «b» виберіть сторону, яка дорівнює 4 см.
- Висота:
- Спростіть квадратний корінь за допомогою множників:
- S
- Відповідь можна записати з коренем або витягти корінь на калькуляторі і записати відповідь у вигляді десяткового дробу (S ≈ 15,49 см2).
Метод2 З 2:
Як обчислити площу з допомогою тригонометричних функцій
Метод2 З 2:
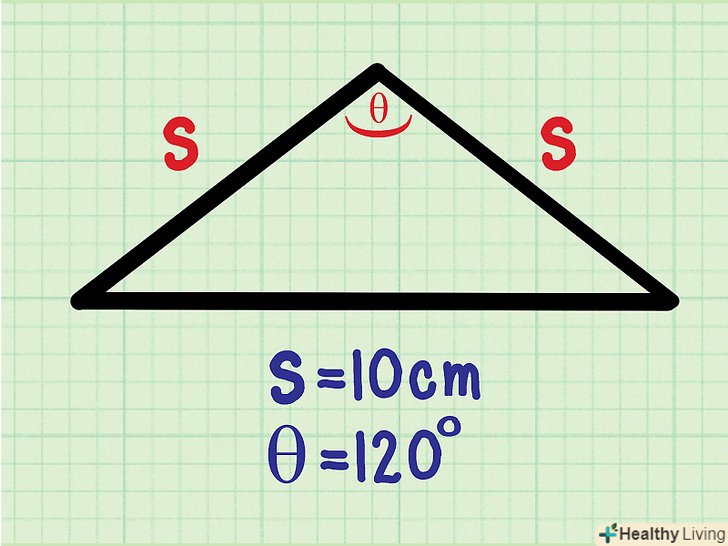
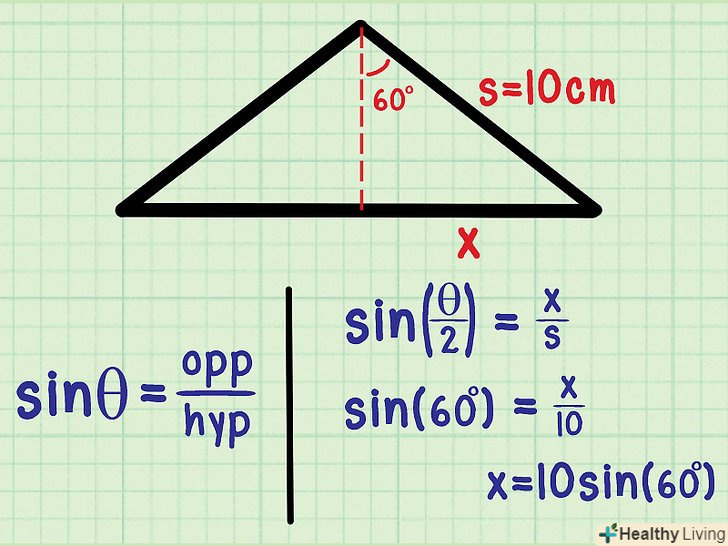
 Обчисліть площу по бічній стороні і прилеглому кутку. якщо Ви знайомі з тригонометричними функціями, площа рівнобедреного трикутника можна обчислити по бічній стороні і прилеглому кутку. Наприклад: [3]
Обчисліть площу по бічній стороні і прилеглому кутку. якщо Ви знайомі з тригонометричними функціями, площа рівнобедреного трикутника можна обчислити по бічній стороні і прилеглому кутку. Наприклад: [3]- Бічна сторона рівнобедреного трикутника дорівнює 10 см.
- Кут θ між двома рівними сторонами дорівнює 120°.
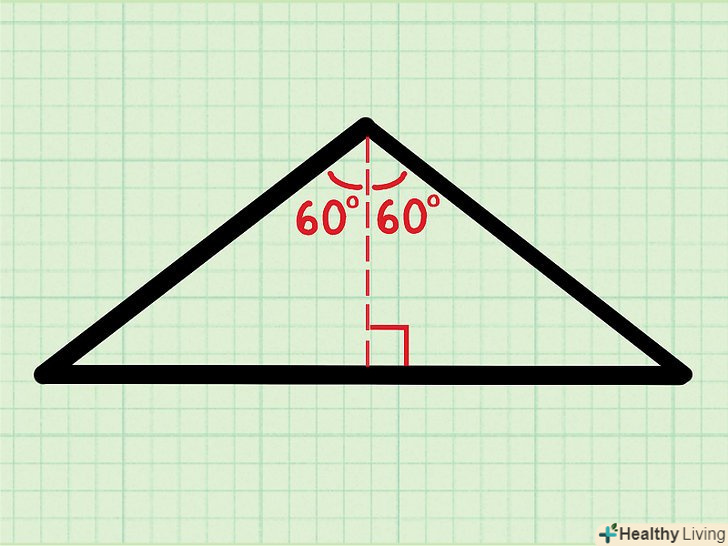
 Розділіть рівнобедрений трикутник на два рівних прямокутних трикутника.для цього опустіть перпендикуляр (висоту) з вершини трикутника, Яка утворена двома рівними сторонами, на підставу.
Розділіть рівнобедрений трикутник на два рівних прямокутних трикутника.для цього опустіть перпендикуляр (висоту) з вершини трикутника, Яка утворена двома рівними сторонами, на підставу.- Висота ділить кут θ рівно навпіл. Таким чином, один з кутів прямокутного трикутника дорівнює ½θ, а в нашому прикладі ( ½ ) (120) = 60°.
 Обчисліть висоту " h " за допомогою тригонометричних функцій.до прямокутного трикутника можна застосувати наступні тригонометричні функції: sin (синус), cos (косинус) і tg (тангенс). У нашому прикладі відома гіпотенуза "s«; потрібно знайти» h", тобто катет, прилеглий до відомого кутку. Згадайте, що косинус = прилеглий катет / гіпотенуза.
Обчисліть висоту " h " за допомогою тригонометричних функцій.до прямокутного трикутника можна застосувати наступні тригонометричні функції: sin (синус), cos (косинус) і tg (тангенс). У нашому прикладі відома гіпотенуза "s«; потрібно знайти» h", тобто катет, прилеглий до відомого кутку. Згадайте, що косинус = прилеглий катет / гіпотенуза.- Cos(θ/2) = h/s
- Cos(60°) = h/10
- H = 10cos(60º)
 Обчисліть значення другого катета.тепер ми не знаємо значення другого катета прямокутного трикутника; позначимо його як «x». Згадайте, що синус = протилежний катет / гіпотенуза.
Обчисліть значення другого катета.тепер ми не знаємо значення другого катета прямокутного трикутника; позначимо його як «x». Згадайте, що синус = протилежний катет / гіпотенуза.- Sin(θ/2) = x/s
- Sin(60º) = x/10
- X = 10sin(60°)
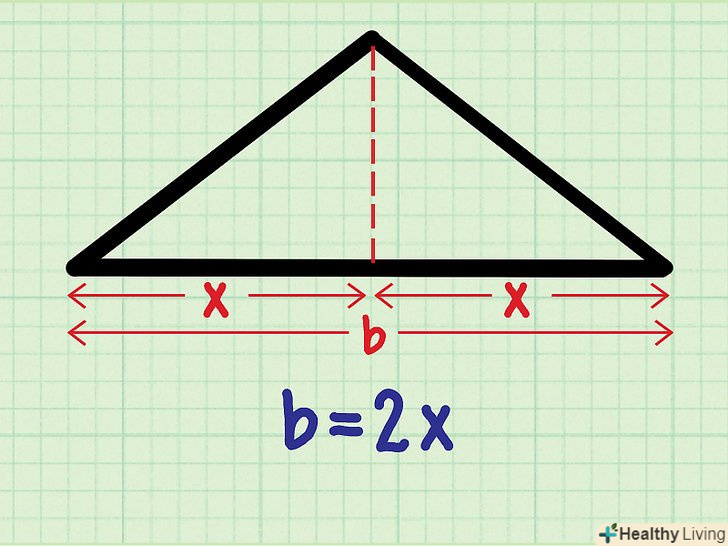
 Зверніть увагу, що другий катет прямокутного трикутника дорівнює половині підстави рівнобедреного трикутника. тобто b = 2x, тому що висота (перший катет) розділила підставу навпіл (на два катети, кожен з яких дорівнює значенню «x»).
Зверніть увагу, що другий катет прямокутного трикутника дорівнює половині підстави рівнобедреного трикутника. тобто b = 2x, тому що висота (перший катет) розділила підставу навпіл (на два катети, кожен з яких дорівнює значенню «x»). Підставте значення " h "і» b" в формулу для обчислення площі.тепер, коли ви знаєте основу і висоту, підставте їх у формулу S = ½:
Підставте значення " h "і» b" в формулу для обчислення площі.тепер, коли ви знаєте основу і висоту, підставте їх у формулу S = ½:- Якщо обчислити синус і косинус на калькуляторі, ви знайдете, що S ≈ 43,3 см2. Якщо хочете, скористайтеся властивостями тригонометричних функцій, спростіть відповідь і запишіть його так: S = 50sin(120°).
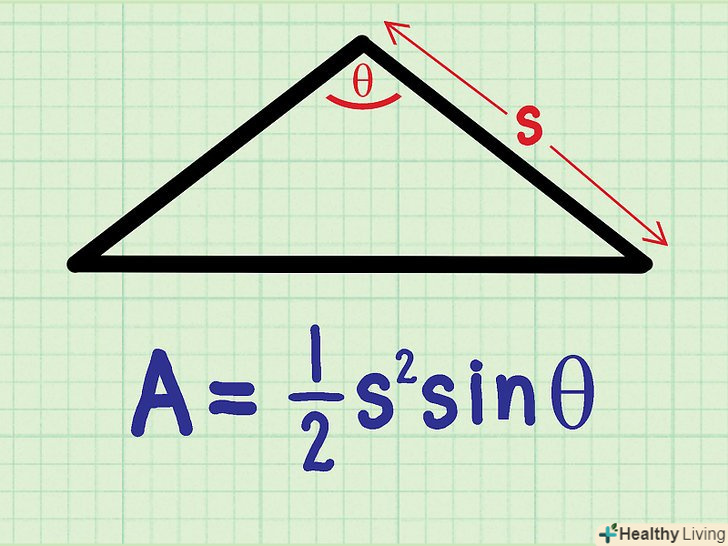
 Запишіть універсальну формулу.тепер, коли ви познайомилися з повним процесом обчислення площі рівнобедреного трикутника, можна користуватися універсальною формулою, яка дозволить скоротити цей процес. Якщо ви повторите описаний процес без числових значень і спростите ряд виразів, ви отримаєте наступну універсальну формулу:[4]
Запишіть універсальну формулу.тепер, коли ви познайомилися з повним процесом обчислення площі рівнобедреного трикутника, можна користуватися універсальною формулою, яка дозволить скоротити цей процес. Якщо ви повторите описаний процес без числових значень і спростите ряд виразів, ви отримаєте наступну універсальну формулу:[4]- S-одна з двох бічних (рівних) сторін.
- Θ-кут між двома бічними (рівними) сторонами.
Поради
- Якщо дано рівнобедрений прямокутний трикутник (з двома рівними катетами і прямим кутом), обчислити його площа дуже просто. Один катет буде підставою, а другий – висотою, тому формула S = ½bh запишеться так: S=½s2, де s – катет.
- З квадратного кореня можна витягти два значення-позитивне і негативне, але в геометричних задачах негативним значенням можна знехтувати. Наприклад, висота трикутника не може бути негативною.
- У деяких завданнях будуть дані інші величини, наприклад, підстава і один кут рівнобедреного трикутника. В цьому випадку дійте так само: розділіть рівнобедрений трикутник на два рівних прямокутних трикутника, а потім знайдіть висоту за допомогою тригонометричних функцій.