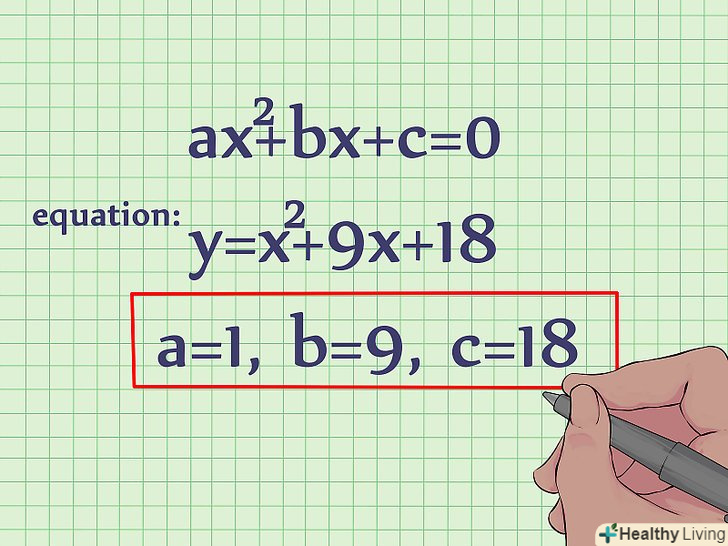Окружність-двовимірна фігура, всі точки якої рівновіддалені від деякої точки (центру кола).
Кроки
Частина1 З 2:
Математичні властивості кола
Частина1 З 2:
- Центр кола-це точка, що лежить всередині кола і рівновіддалена від усіх точок, що лежать на окружності.
- Радіус кола-це відрізок, що з'єднує центр кола і будь-яку точку, що лежить на ній.
- Діаметр кола-це відрізок, що з'єднує будь-які дві точки, що лежать на окружності, і проходить через центр кола.
- Діаметр завжди дорівнює двом радіусам. Якщо ви знаєте радіус, помножте його на 2, щоб отримати діаметр; якщо ви знаєте діаметр, розділіть його на 2, щоб отримати радіус.
- Запам'ятайте, що відрізок, що з'єднує будь-які дві точки, що лежать на окружності, але не проходить через центр кола, не є діаметром. Він називається хордою, яка завжди менше діаметра.
- Позначення кола.окружність позначається символом у вигляді гуртка з крапкою посередині. Для позначення центру кола намалюйте її символ і поруч запишіть букву, що позначає центр кола.
- Окружність з центром в точці О позначається наступним чином: ⊙о.
Частина2 З 2:
Побудова кола
Частина2 З 2:
- Рівняння кола має вигляд: (x – a)2 + (y-b) 2 = r2, де «a» і «b» - координати центру кола (по осі Х і осі Y, відповідно); " r " - радіус кола.
- Як приклад розглянемо рівняння x2 + y2 = 16.
- Знайдіть центр кола.у рівнянні кола центр задається постійними» a «і»b". Якщо вони відсутні (як у нашому прикладі), то вони дорівнюють 0.
- Рівняння в нашому прикладі можна переписати так: (х - 0)2 + (у - 0)2 = 16. Так як а = 0 і b = 0, то центр кола знаходиться в точці (0,0) (на початку координат).
- Знайдіть радіус кола.для цього витягніть корінь з числа, що стоїть за знаком рівності.
- У нашому прикладі R = кв. корінь (16) = 4.
- Нанесіть радіус на координатну площину.позначте точки з координатами (0, r); (0,-r); (r,0); (- r,0), де R – значення радіуса.
- У нашому прикладі нанесіть точки з координатами (0,4); (0,-4); (4,0); (-4,0).
- З'єднайте точки плавної кривої.