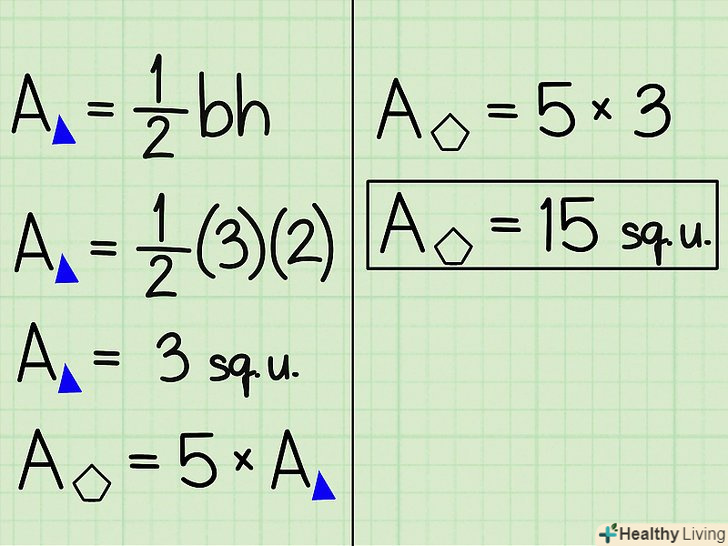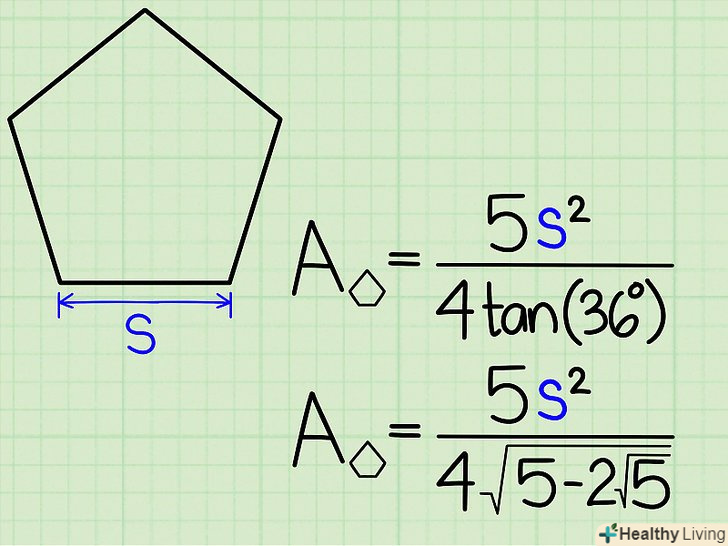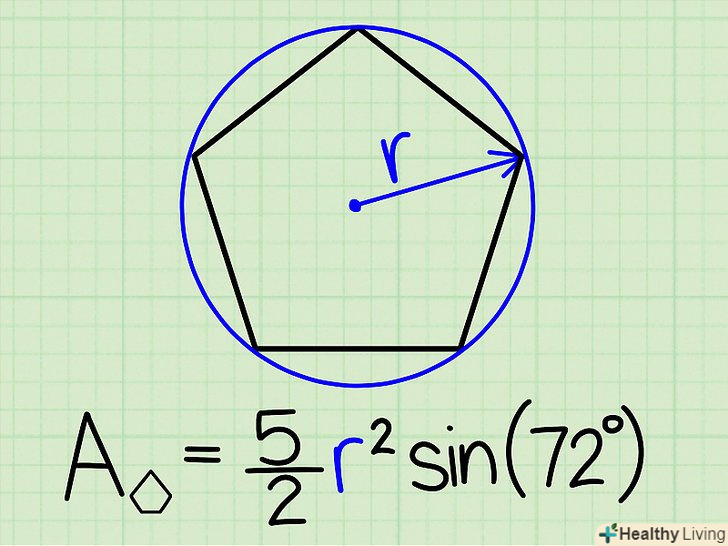П'ятикутник-це багатокутник, у якого п'ять кутів. У переважній більшості завдань ви зіткнетеся з правильним п'ятикутником, у якого всі сторони рівні. Є два основних способи знайти площу п'ятикутника (в залежності від відомих вам величин).
Кроки
Метод1З 3:
Обчислення площі по відомій стороні і апофемі
Метод1З 3:
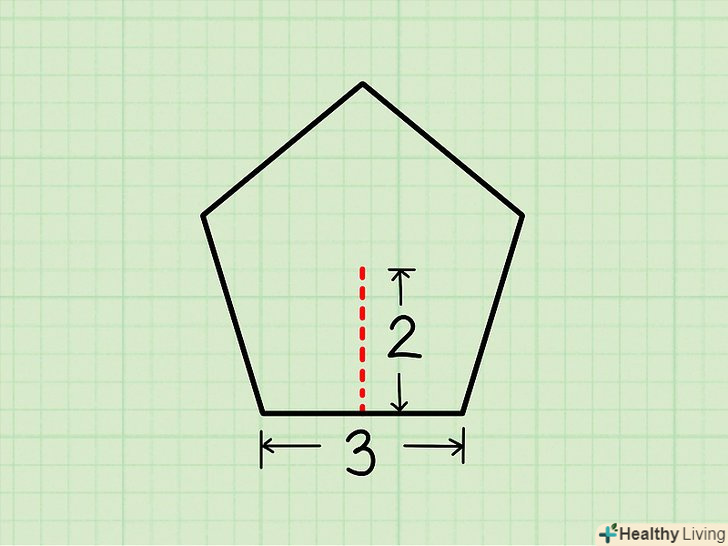
 Дані сторона і апофема.цей метод застосуємо до правильних п'ятикутників, у яких всі сторони рівні. Апофема-це відрізок, що з'єднує центр п'ятикутника і середину будь-якої з його сторін; апофема завжди перпендикулярна стороні п'ятикутника.
Дані сторона і апофема.цей метод застосуємо до правильних п'ятикутників, у яких всі сторони рівні. Апофема-це відрізок, що з'єднує центр п'ятикутника і середину будь-якої з його сторін; апофема завжди перпендикулярна стороні п'ятикутника.- Не плутайте апофему з радіусом описаного кола. Такий радіус-це відрізок, що з'єднує центр п'ятикутника з його вершиною (а не серединою боку). Якщо вам дана сторона і радіус описаного кола, перейдіть до наступного розділу.
- Наприклад, дано п'ятикутник зі стороною3 см і апофемою 2 см.
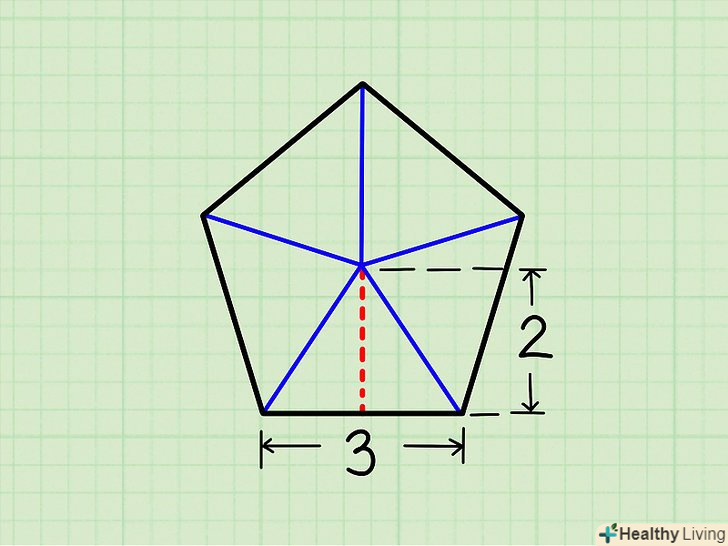
 Розділіть п'ятикутник на п'ять рівних трикутників.для цього з'єднайте центр п'ятикутника з кожною з його вершин.
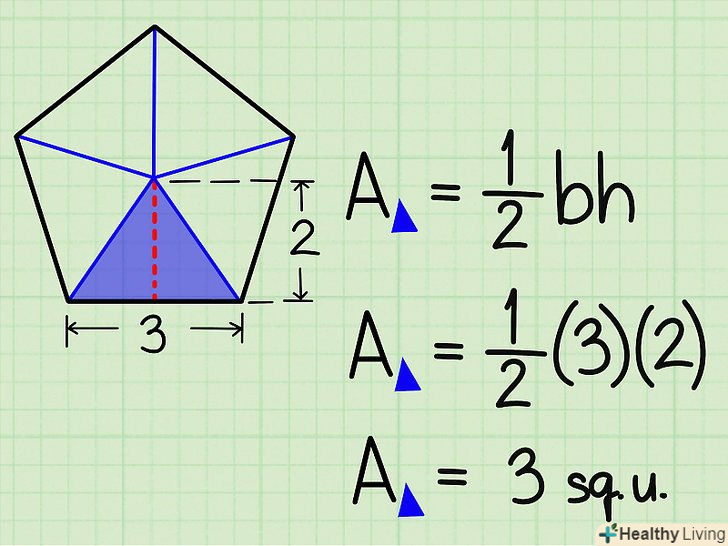
Розділіть п'ятикутник на п'ять рівних трикутників.для цього з'єднайте центр п'ятикутника з кожною з його вершин. Обчисліть площу трикутника.основа кожного трикутника-це сторона п'ятикутника, а висота кожного трикутника — це апофема п'ятикутника. Для обчислення площі трикутника перемножте половину підстави і висоту, тобто площа = ½ х підстава х висоту.
Обчисліть площу трикутника.основа кожного трикутника-це сторона п'ятикутника, а висота кожного трикутника — це апофема п'ятикутника. Для обчислення площі трикутника перемножте половину підстави і висоту, тобто площа = ½ х підстава х висоту.- У нашому прикладі площа трикутника = ½ х 3 х 2 =3 квадратних сантиметри.
 Помножте знайдену площу трикутника на 5, щоб обчислити площу п'ятикутника.це вірно, оскільки ми розділили п'ятикутник на п'ять рівних трикутників.
Помножте знайдену площу трикутника на 5, щоб обчислити площу п'ятикутника.це вірно, оскільки ми розділили п'ятикутник на п'ять рівних трикутників.- У нашому прикладі площа п'ятикутника = 5 х площа трикутника = 5 х 3 = 15 квадратних сантиметрів.
Метод2 З 3:
Обчислення площі по відомій стороні
Метод2 З 3:
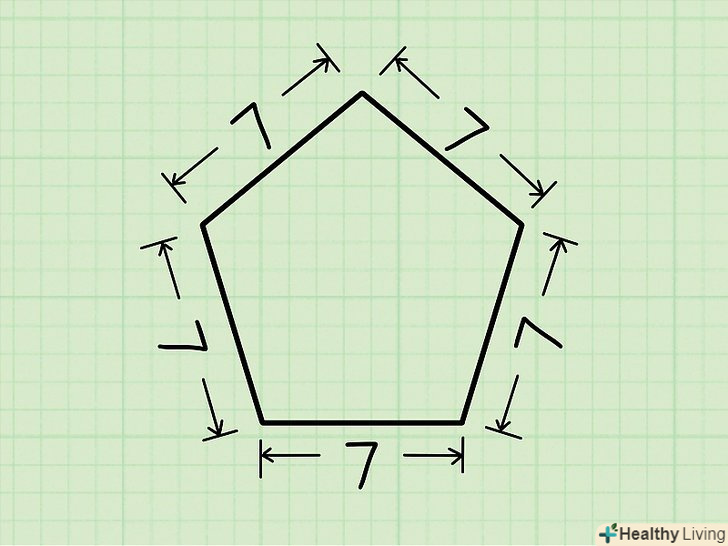
 Якщо дана сторона.цей метод застосуємо до правильних п'ятикутників, у яких всі сторони рівні.
Якщо дана сторона.цей метод застосуємо до правильних п'ятикутників, у яких всі сторони рівні.- Наприклад, дано п'ятикутник зі стороною7 див.
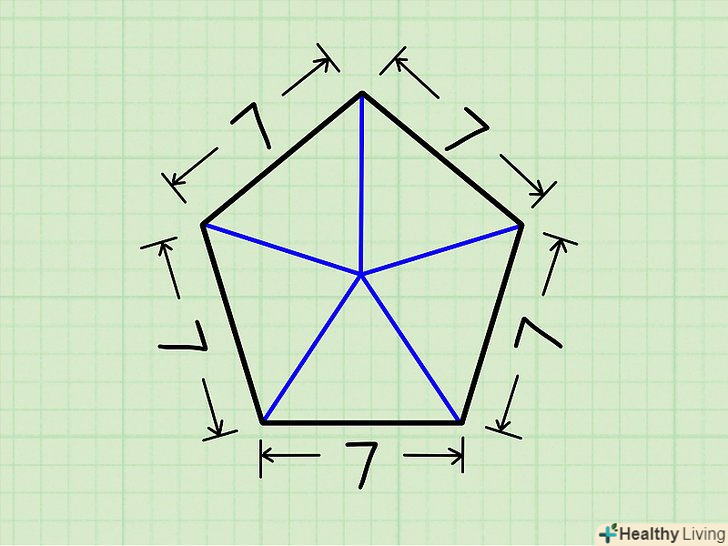
 Розділіть п'ятикутник на п'ять рівних трикутників.для цього з'єднайте центр п'ятикутника з кожною з його вершин.
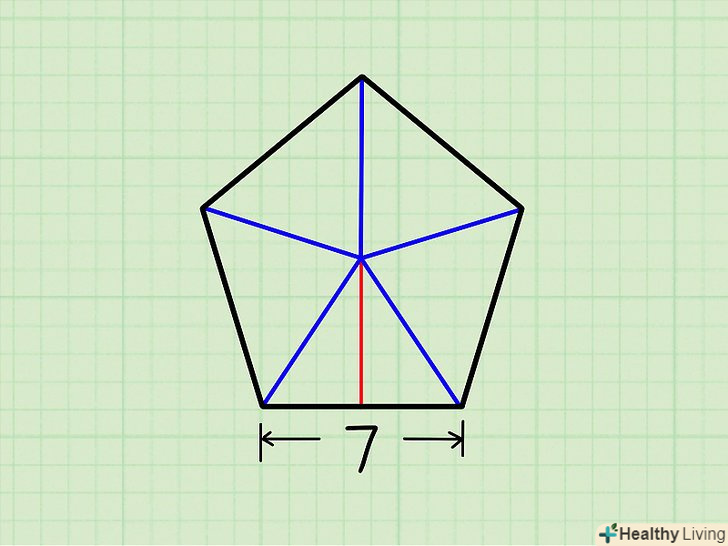
Розділіть п'ятикутник на п'ять рівних трикутників.для цього з'єднайте центр п'ятикутника з кожною з його вершин. Розділіть трикутник навпіл.для цього з вершини трикутника, Яка лежить в центрі п'ятикутника, опустіть перпендикуляр до протилежної сторони трикутника, Яка дорівнює стороні п'ятикутника. Ви отримаєте два рівних прямокутних трикутника.
Розділіть трикутник навпіл.для цього з вершини трикутника, Яка лежить в центрі п'ятикутника, опустіть перпендикуляр до протилежної сторони трикутника, Яка дорівнює стороні п'ятикутника. Ви отримаєте два рівних прямокутних трикутника. Дайте позначення одному з прямокутних трикутників.
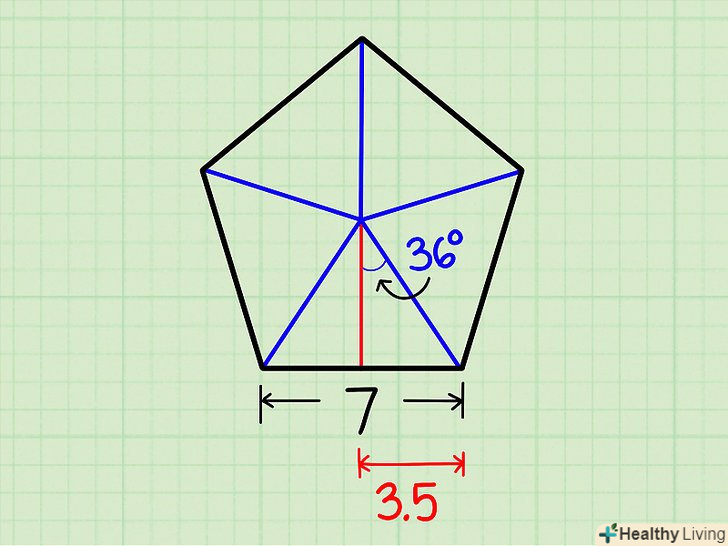
Дайте позначення одному з прямокутних трикутників.- Основа прямокутного трикутника-це половина сторони п'ятикутника. У нашому прикладі підстава дорівнює ½ х 7 = 3,5 см.
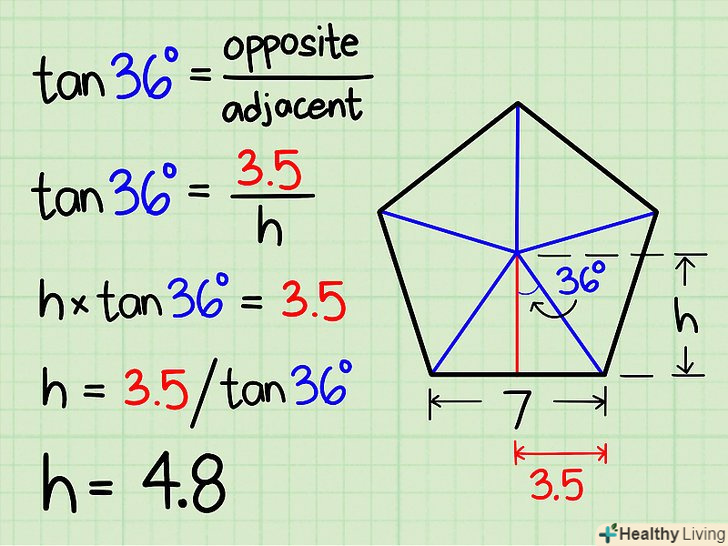
- Кут навколо центру п'ятикутника дорівнює 360. Розділивши п'ятикутник на п'ять рівних трикутників, а потім розділивши кожен трикутник навпіл, ви поділите кут навколо центру п'ятикутника на 10 рівних частин, тобто кут прямокутного трикутника, протилежний основи, дорівнює 360°/10 = 36.
 Обчисліть висоту трикутника. Висота прямокутного трикутника дорівнює його катету, відмінному від основи. Використовуйтетригонометричні функції, щоб знайти висоту трикутника.[1]
Обчисліть висоту трикутника. Висота прямокутного трикутника дорівнює його катету, відмінному від основи. Використовуйтетригонометричні функції, щоб знайти висоту трикутника.[1]- У прямокутному трикутникуТангенс кута дорівнює відношенню протилежної сторони до прилеглої стороні.
- У нашому прикладі для кута в 36 протилежної стороною є підстава, а прилеглої — висота.
- Tg 36 = протилежна сторона / прилегла сторона
- У нашому прикладі tg 36 = 3,5 / висота
- Висота х tg 36 = 3,5
- Висота = 3,5 / tg 36
- Висота =4,8 см (приблизно)
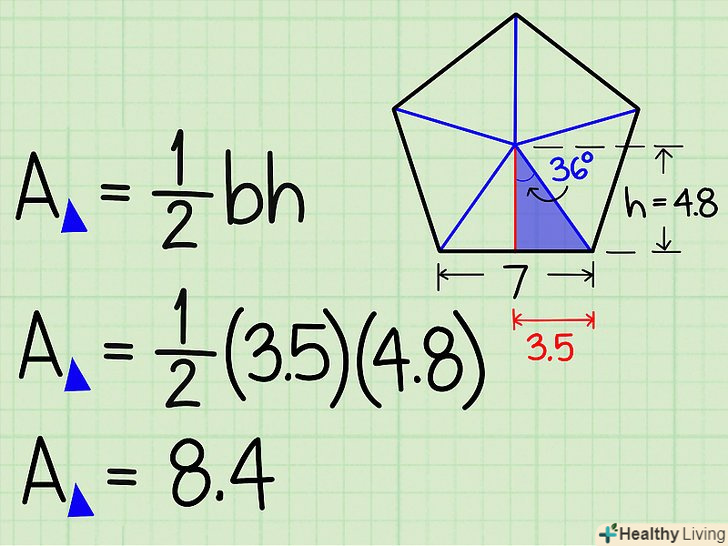
 Знайдіть площу трикутника. площа трикутника = ½ х підстава х Висота (а=½). Знаючи основу і висоту, ви можете знайти площу прямокутного трикутника.
Знайдіть площу трикутника. площа трикутника = ½ х підстава х Висота (а=½). Знаючи основу і висоту, ви можете знайти площу прямокутного трикутника.- У нашому прикладі площа прямокутного трикутника = ½ (3,5) (4,8) = 8,4 квадратних сантиметрів.
 Помножте знайдену площу прямокутного трикутника на 10, щоб обчислити площу п'ятикутника.це вірно, оскільки ми розділили п'ятикутник на десять рівних прямокутних трикутників.
Помножте знайдену площу прямокутного трикутника на 10, щоб обчислити площу п'ятикутника.це вірно, оскільки ми розділили п'ятикутник на десять рівних прямокутних трикутників.- У нашому прикладі площа п'ятикутника дорівнює 8,4 х 10 =84 квадратних сантиметра.
Метод3 З 3:
Формули
Метод3 З 3:
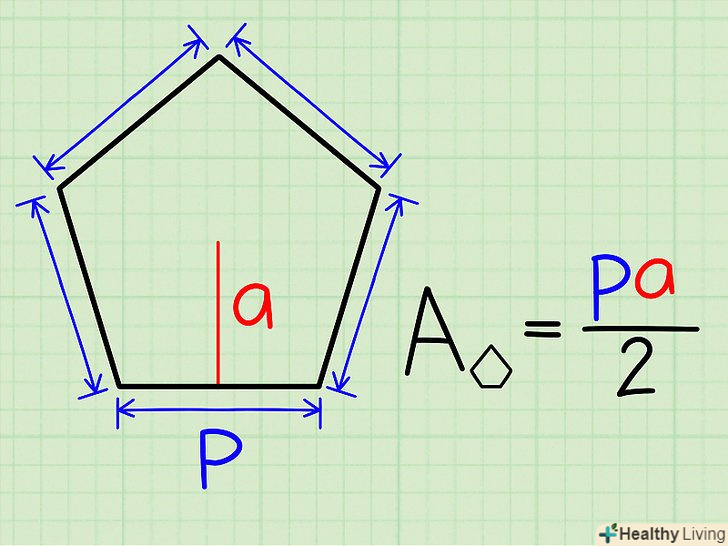
 Дані периметр і апофема.Апофема-це відрізок, що з'єднує центр п'ятикутника і середину будь-якої з його сторін; апофема завжди перпендикулярна стороні п'ятикутника.
Дані периметр і апофема.Апофема-це відрізок, що з'єднує центр п'ятикутника і середину будь-якої з його сторін; апофема завжди перпендикулярна стороні п'ятикутника.- A = ра/2, де р — периметр, А — апофема. [2]
- Якщо дана сторона, обчисліть периметр правильного п'ятикутника за формулою: p = 5s, де s — сторона п'ятикутника.

 Дано радіус описаного кола. У цьому випадку для обчислення площі п'ятикутника використовуйте наступну формулу:[5]
Дано радіус описаного кола. У цьому випадку для обчислення площі п'ятикутника використовуйте наступну формулу:[5]- A = (5/2)r2sin72, де r — радіус описаного кола.
Поради
- Складніше працювати з неправильним п'ятикутником (це п'ятикутник, сторони якого мають різну довжину). В цьому випадку розділіть п'ятикутник на трикутники, знайдіть їх площі і складіть значення площ. Ви також можете змалювати п'ятикутник правильною фігурою, обчислити її площу, а потім відняти площу додаткового простору.
- Формули, отримані геометричним шляхом, аналогічні формулам, які описані в цій статті. Подумайте, чи зможете ви вивести ці формули. Формулу, що включає радіус описаного кола, вивести важче (натяк: розглядайте подвоєний кут при Центрі п'ятикутника).
- У наведених у цій статті прикладах використовуються округлені значення, щоб спростити обчислення. Якщо ви працюєте з реальним багатокутником, то ви отримаєте інші результати для інших довжин і площ.
- Якщо можливо, обчисліть площу п'ятикутника, використовуючи обидва описаних методу. Потім порівняйте результати, щоб підтвердити правильність відповіді.
Джерела
- ↑ Https://www.mathsisfun.com/geometry/regular-polygons.html
- ↑ Https://www.mathsisfun.com/geometry/regular-polygons.html
- ↑ Http://www.mathopenref.com/polygonregulararea.html
- ↑ Http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/simpleTrig.html
- ↑ Http://www.mathopenref.com/polygonregularareaderive.html