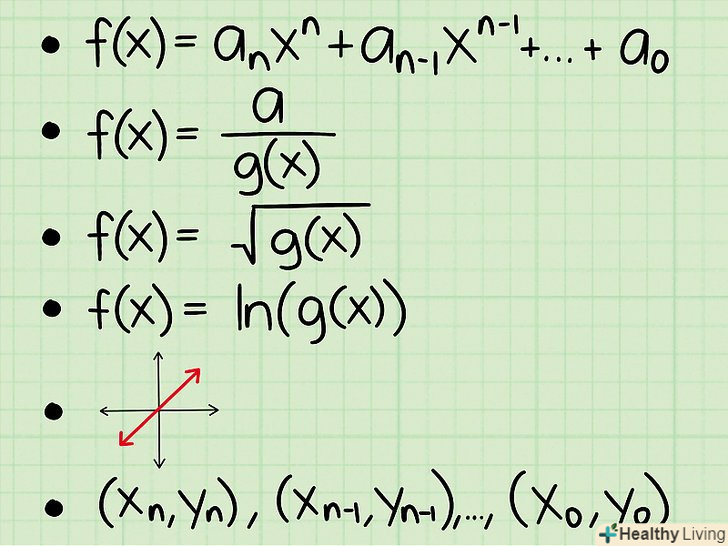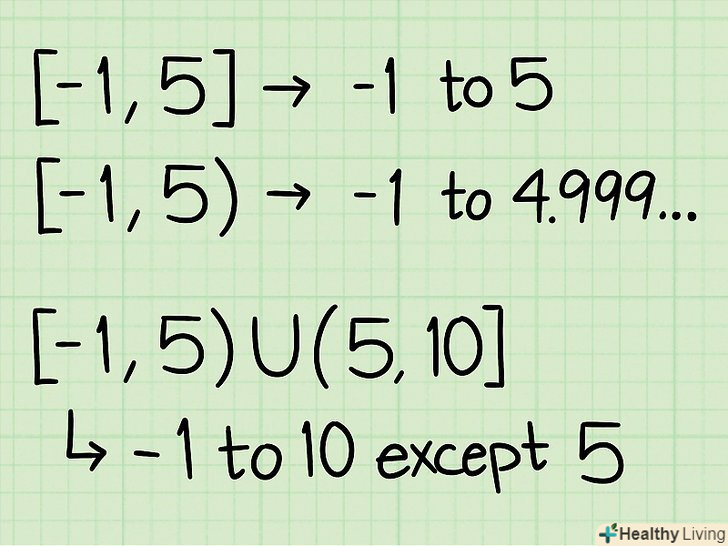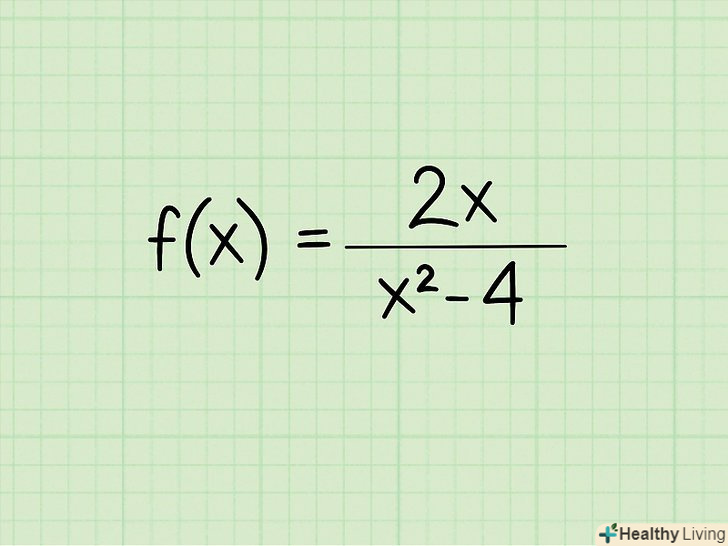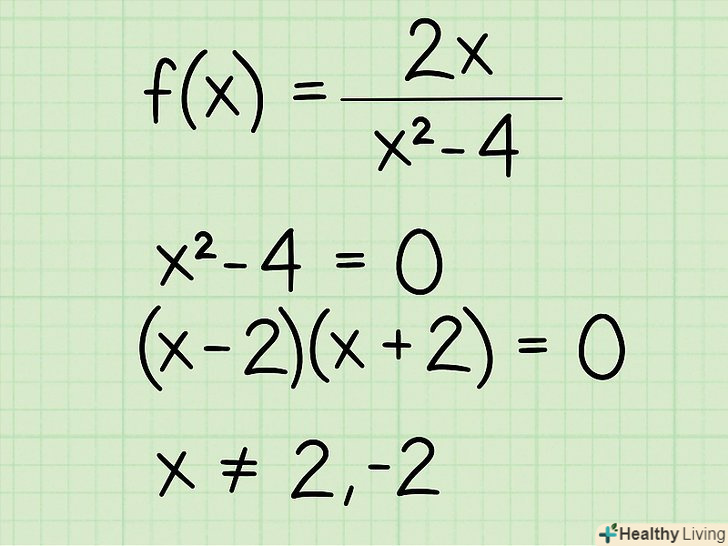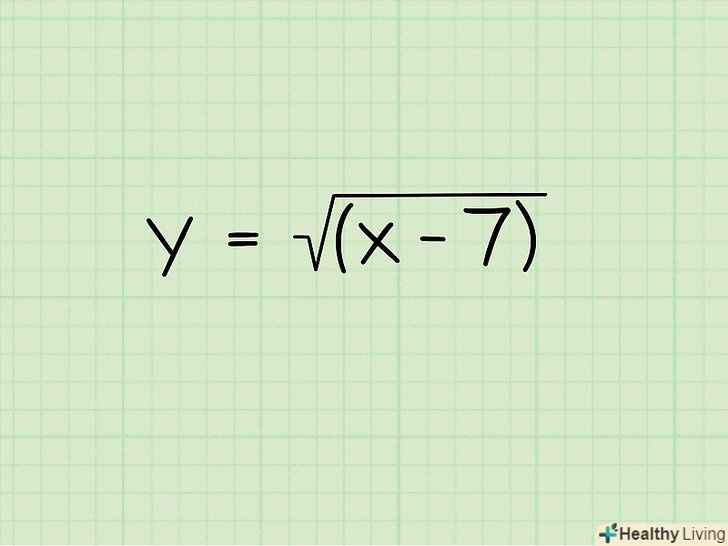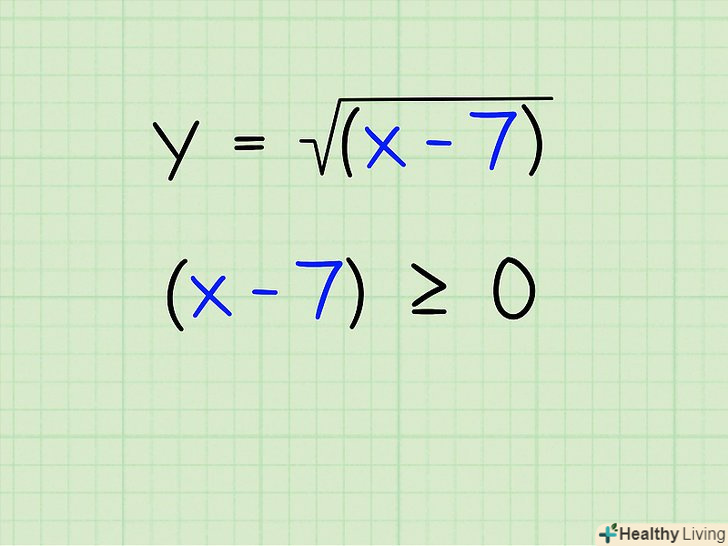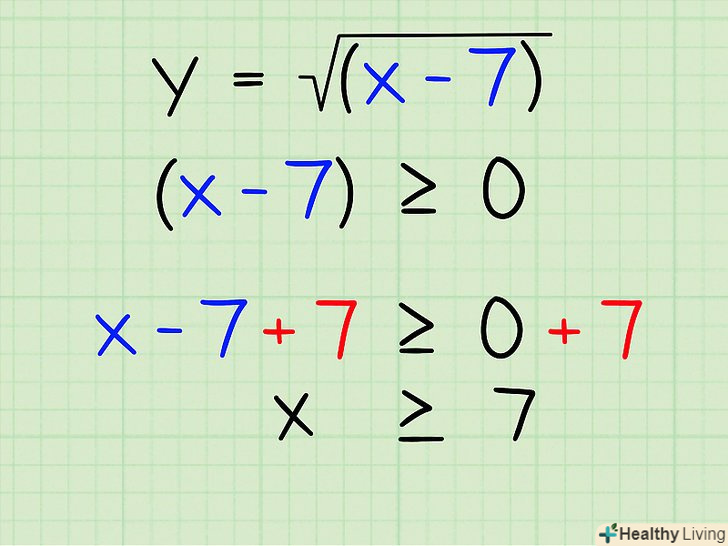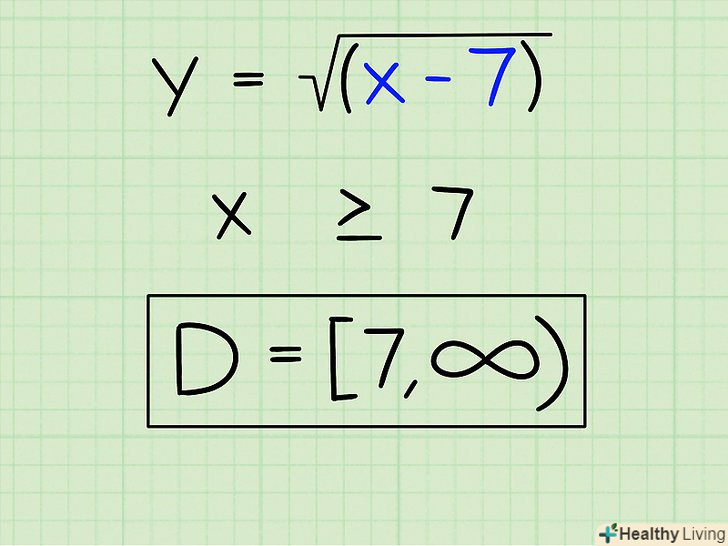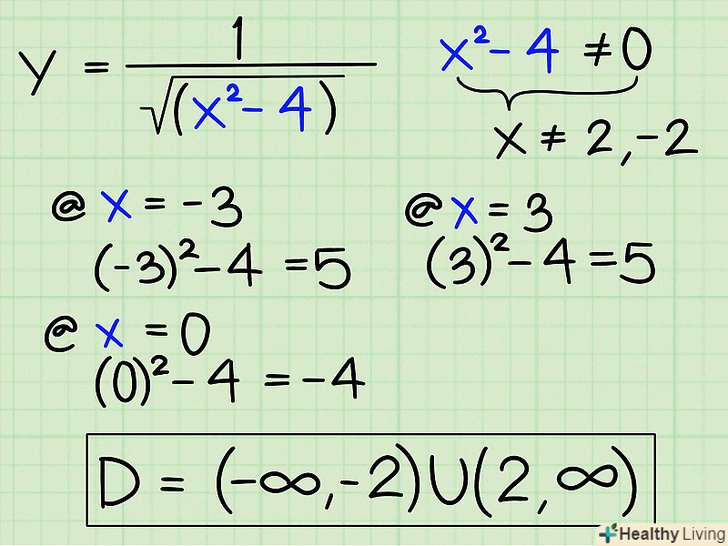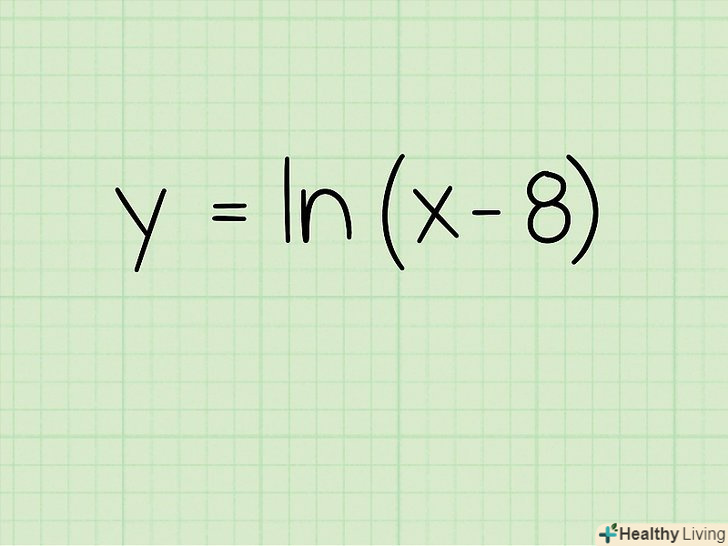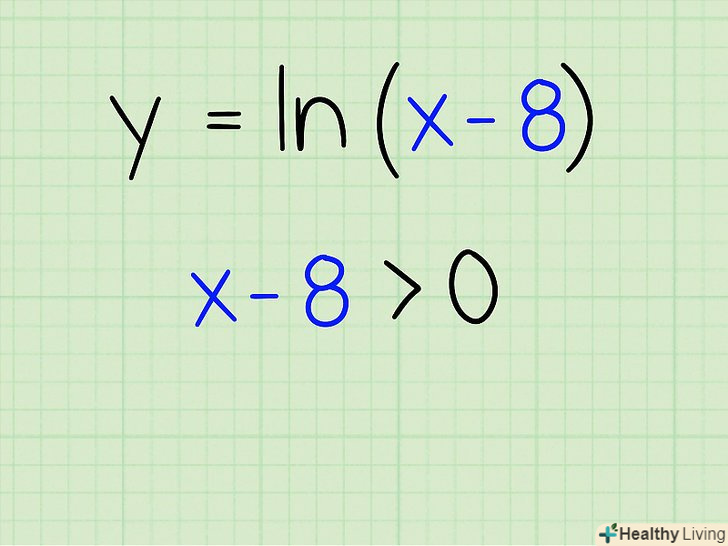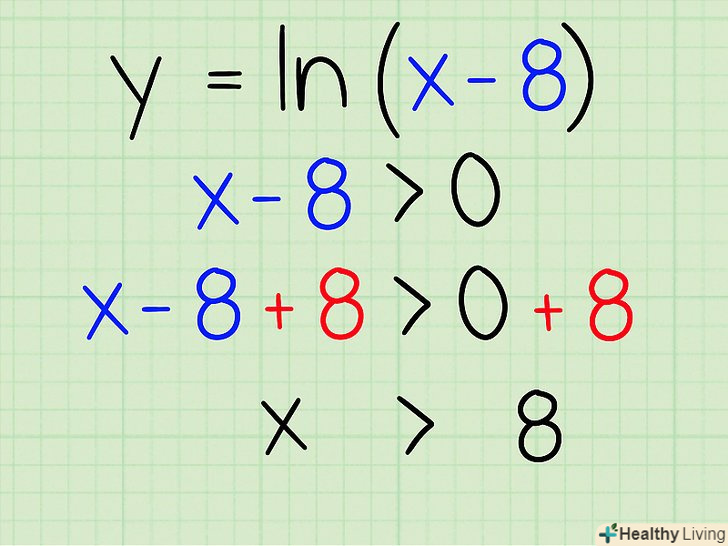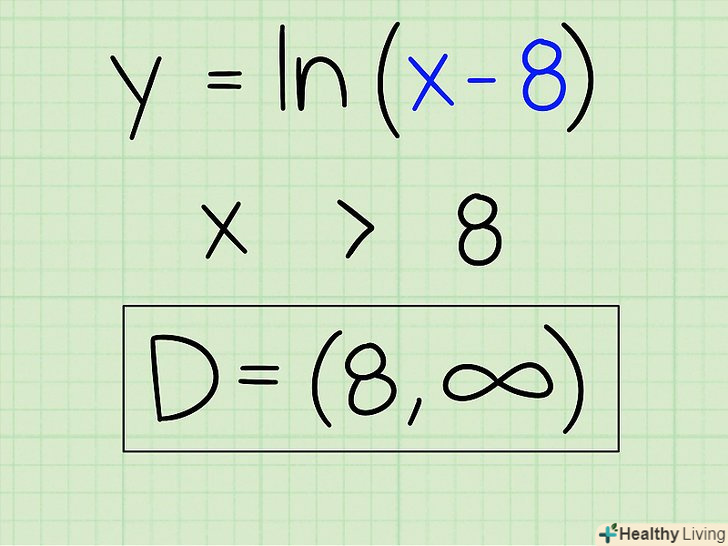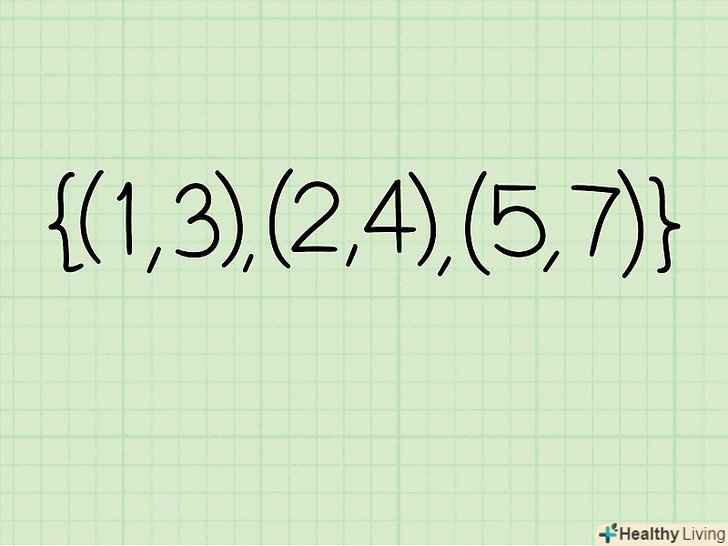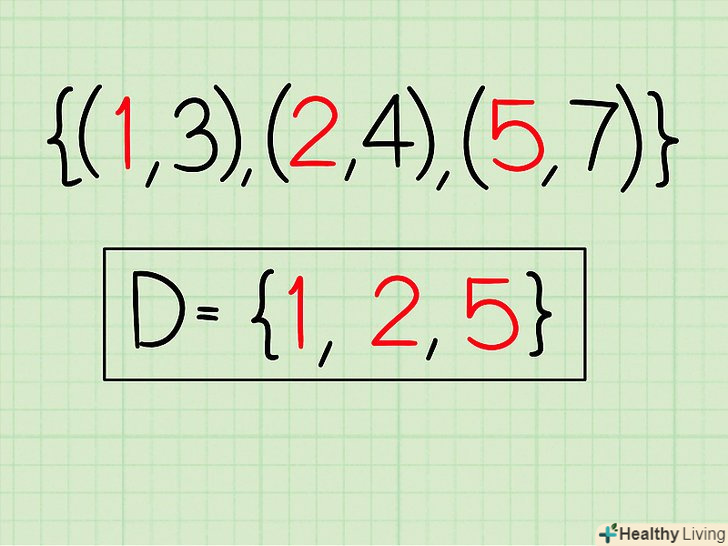Область визначення функції-це множина чисел, на якій задається функція. Іншими словами, це ті значення х, які можна підставити в дане рівняння. Можливі значення у називаються областю значень функції. Якщо ви хочете знайти область визначення функції в різних ситуаціях, виконайте наступні дії.
Кроки
Метод1З 6:
Основи
Метод1З 6:
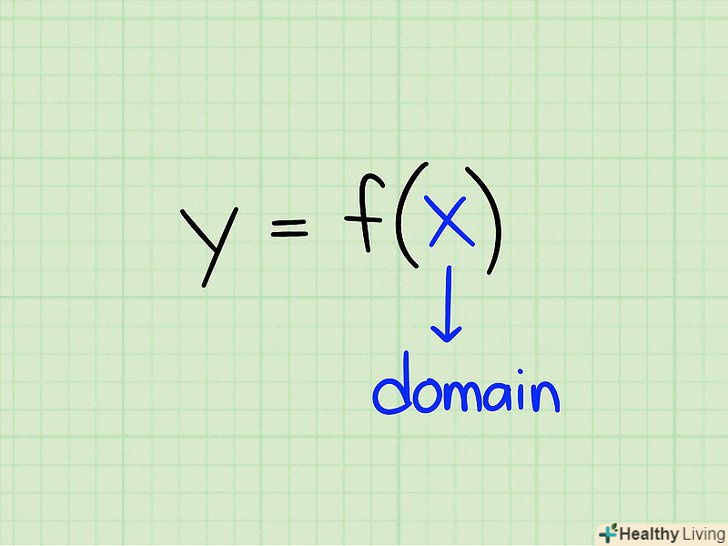
 Запам'ятайте, що таке область визначення.Область визначення-це безліч значень х, при підставленні яких в рівняння ми отримуємо область значень у.
Запам'ятайте, що таке область визначення.Область визначення-це безліч значень х, при підставленні яких в рівняння ми отримуємо область значень у. Навчіться знаходити область визначення різних функцій.тип функції визначає метод знаходження області визначення. Ось основні моменти, які ви повинні знати про кожен тип функції, про які піде мова в наступному розділі:
Навчіться знаходити область визначення різних функцій.тип функції визначає метод знаходження області визначення. Ось основні моменти, які ви повинні знати про кожен тип функції, про які піде мова в наступному розділі:- Поліноміальна функція без коренів або змінних у знаменнику.для цього типу функції областю визначення є всі дійсні числа.
- Дробова функція зі змінною в знаменнику. щоб знайти область визначення даного типу функції, знаменник прирівняйте до нуля і виключіть знайдені значення х.
- Функція зі змінною всередині кореня. щоб знайти область визначення даного типу функції, задайте підкорене вираз більше або дорівнює 0 і знайдіть значення х.
- Функція з натуральним логарифмом (ln). Задайте вираз під логарифмом &#gt; 0 і вирішіть.
- Графік. намалюйте графік для знаходження х.
- Безліч. це буде список координат х і у. Область визначення — список координат х.
 Правильно позначайте область визначення. легко навчитися правильному позначенню області визначення, але важливо, щоб ви правильно записували відповідь і отримували високу оцінку. Ось кілька речей, які ви повинні знати про написання області визначення:
Правильно позначайте область визначення. легко навчитися правильному позначенню області визначення, але важливо, щоб ви правильно записували відповідь і отримували високу оцінку. Ось кілька речей, які ви повинні знати про написання області визначення:- Один з форматів написання області визначення: квадратна дужка, 2 кінцевих значення області, кругла дужка.
- Наприклад, [-1; 5). Це означає область визначення від -1 до 5.
- Використовуйте квадратні дужки [ і ] , щоб вказати, що значення належить області визначення.
- Таким чином, у прикладі [-1; 5) область включає -1.
- Використовуйте круглі дужки ( і ) , щоб вказати, що значення не належить області визначення.
- Таким чином, у прикладі [-1; 5) 5 не належить області. Область включає тільки значення, нескінченно близькі до 5, тобто 4,999 (9).
- Використовуйте знак U для об'єднання областей, розділених проміжком.
- Наприклад, [-1; 5 ) U (5; 10]. Це означає, Що область проходить від -1 до 10 включно, але не включає 5. Це може бути у функції, де в знаменнику стоїть "х - 5".
- Ви можете використовувати кілька U, якщо потрібно, якщо область має кілька розривів / проміжків.
- Використовуйте знаки "плюс нескінченність" і "мінус нескінченність", щоб висловити, що область нескінченна в будь-якому напрямку.
- Зі знаком нескінченності завжди використовуйте (), а не [ ].
- Один з форматів написання області визначення: квадратна дужка, 2 кінцевих значення області, кругла дужка.
Метод2З 6:
Область визначення дробових функцій
Метод2З 6:
 Запишіть приклад.наприклад, вам дана наступна функція:
Запишіть приклад.наприклад, вам дана наступна функція:- F(x) = 2x/(x2 - 4)
 Для дробових функцій зі змінною в знаменнику треба прирівняти знаменник до нуля.при знаходженні області визначення дробової функції необхідно виключити всі значення х, при яких знаменник дорівнює нулю, тому що не можна ділити на нуль. Запишіть знаменник як рівняння і прирівняйте його до 0. Ось як це робиться:
Для дробових функцій зі змінною в знаменнику треба прирівняти знаменник до нуля.при знаходженні області визначення дробової функції необхідно виключити всі значення х, при яких знаменник дорівнює нулю, тому що не можна ділити на нуль. Запишіть знаменник як рівняння і прирівняйте його до 0. Ось як це робиться:- F(x) = 2x/(x2 - 4)
- X2 - 4 = 0
- (x - 2 )(x + 2) = 0
- X ≠ 2; - 2
 Запишіть область визначення:
Запишіть область визначення:- Х = всі дійсні числа, крім 2 і -2
Метод3З 6:
Область визначення функції з коренем
Метод3З 6:
 Запишіть приклад.Дана функція y =√(x-7)
Запишіть приклад.Дана функція y =√(x-7) Задайте підкорене вираз більше або рівним 0. ви не можете витягти квадратний корінь з негативного числа, хоча ви можете витягти квадратний корінь 0. Таким чином, задайте підкорене вираз більше або рівним 0. Зауважимо, що це відноситься не тільки до квадратним коріння, але і до всіх коренів з парною ступенем. Тим не менш, це не стосується коріння з непарним ступенем, так як негативне число може стояти під коренем непарного ступеня.
Задайте підкорене вираз більше або рівним 0. ви не можете витягти квадратний корінь з негативного числа, хоча ви можете витягти квадратний корінь 0. Таким чином, задайте підкорене вираз більше або рівним 0. Зауважимо, що це відноситься не тільки до квадратним коріння, але і до всіх коренів з парною ступенем. Тим не менш, це не стосується коріння з непарним ступенем, так як негативне число може стояти під коренем непарного ступеня.- Х-7 ≧ 0
 Виділіть змінну.для цього перенесіть 7 в праву частину нерівності:
Виділіть змінну.для цього перенесіть 7 в праву частину нерівності:- X ≧ 7
 Запишіть область визначення. Ось вона:
Запишіть область визначення. Ось вона:- D = [7; +∞)
 Знайдіть область визначення функції з коренем, коли є кілька рішень. Дано: y = 1/√ (x2 -4). Прирівнявши знаменник до нуля і вирішивши це рівняння, ви отримаєте х ≠ (2; -2). Ось як ви дієте далі:
Знайдіть область визначення функції з коренем, коли є кілька рішень. Дано: y = 1/√ (x2 -4). Прирівнявши знаменник до нуля і вирішивши це рівняння, ви отримаєте х ≠ (2; -2). Ось як ви дієте далі:- Перевірте область за -2 (наприклад, підставивши -3), щоб упевнитися, що підстановка в знаменник чисел менше -2 в результаті дає число більше 0. І це так:
- (-3)2 - 4 = 5
- Тепер перевірте область між -2 і +2. Підставте, наприклад, 0.
- 02 - 4 = -4, так що числа між -2 і 2 не підходять.
- Тепер спробуйте числа більше 2, наприклад 3.
- 32 - 4 = 5, так що числа більше 2 підходять.
- Запишіть область визначення. Ось як записується ця область:
- D = (-∞; -2) U (2; +∞)
- Перевірте область за -2 (наприклад, підставивши -3), щоб упевнитися, що підстановка в знаменник чисел менше -2 в результаті дає число більше 0. І це так:
Метод4З 6:
Область визначення функції з натуральним логарифмом
Метод4З 6:
 Запишіть приклад.припустимо, дана функція:
Запишіть приклад.припустимо, дана функція:- F(x) = ln(x - 8)
 Задайте вираз під логарифмом більше нуля. натуральний логарифм повинен бути позитивним числом, тому задаємо вираз всередині дужок більше нуля.
Задайте вираз під логарифмом більше нуля. натуральний логарифм повинен бути позитивним числом, тому задаємо вираз всередині дужок більше нуля.- X - 8 &#gt; 0
 Вирішіть.для цього відокремте змінну х, додавши до обох частин нерівності 8.
Вирішіть.для цього відокремте змінну х, додавши до обох частин нерівності 8.- X - 8 + 8 &#gt; 0 + 8
- X &#gt; 8
 Запишіть область визначення.Область визначення цієї функції є будь-яке число більше 8. Отак:
Запишіть область визначення.Область визначення цієї функції є будь-яке число більше 8. Отак:- D = (8; +∞)
Метод5З 6:
Пошук області визначення за допомогою графіка
Метод5З 6:
 Подивіться на графік.
Подивіться на графік. Перевірте значення х, які відображені на графіку.це може бути легше сказати, ніж зробити, але ось кілька порад:
Перевірте значення х, які відображені на графіку.це може бути легше сказати, ніж зробити, але ось кілька порад:- Лінія. Якщо на графіку ви бачите лінію, яка йде в нескінченність, товсе значення х вірні, і область визначення включає всі дійсні числа.
- Звичайна парабола. Якщо ви бачите параболу, яка дивиться вгору або вниз, то область визначення - всі дійсні числа, тому що підходять всі числа на осі х.
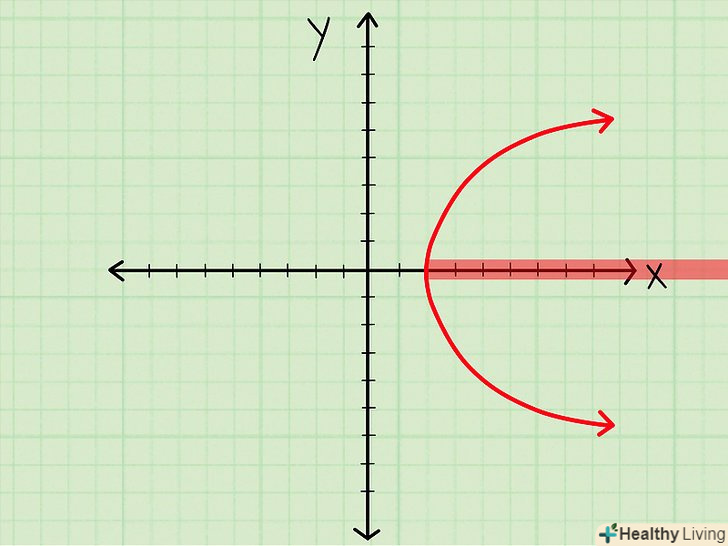
- Лежача парабола. Тепер, якщо у вас є парабола з вершиною в точці (4; 0), яка простягається нескінченно вправо, то область визначення D = [4;+∞)
 Запишіть область визначення.запишіть область визначення залежно від типу графіка, з яким ви працюєте. Якщо ви не впевнені в типі графіка і знаєте функцію, що описує його, для перевірки підставте координати х в функцію.
Запишіть область визначення.запишіть область визначення залежно від типу графіка, з яким ви працюєте. Якщо ви не впевнені в типі графіка і знаєте функцію, що описує його, для перевірки підставте координати х в функцію.
Метод6З 6:
Пошук області визначення за допомогою множини
Метод6З 6:
 Запишіть множину. множина-це набір координат х і у. Наприклад, ви працюєте з наступними координатами: {(1; 3), (2; 4), (5; 7)}
Запишіть множину. множина-це набір координат х і у. Наприклад, ви працюєте з наступними координатами: {(1; 3), (2; 4), (5; 7)} Запишіть координати х. це 1; 2; 5.
Запишіть координати х. це 1; 2; 5. Область визначення: D = {1; 2; 5}
Область визначення: D = {1; 2; 5} Переконайтеся, що множина є функцією.для цього необхідно, щоб кожен раз, коли ви підставляєте значення х, ви отримували одне і те ж значення y. наприклад, підставляючи х = 3, Ви повинні отримати у = 6, і так далі. Наведена в прикладі множина не є функцією, тому що дано два різних значення у: {(1; 4), (3; 5), (1; 5)}.
Переконайтеся, що множина є функцією.для цього необхідно, щоб кожен раз, коли ви підставляєте значення х, ви отримували одне і те ж значення y. наприклад, підставляючи х = 3, Ви повинні отримати у = 6, і так далі. Наведена в прикладі множина не є функцією, тому що дано два різних значення у: {(1; 4), (3; 5), (1; 5)}.