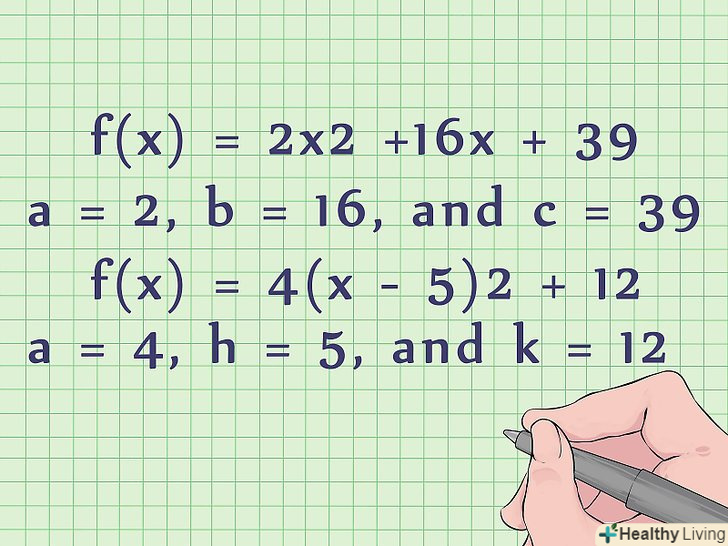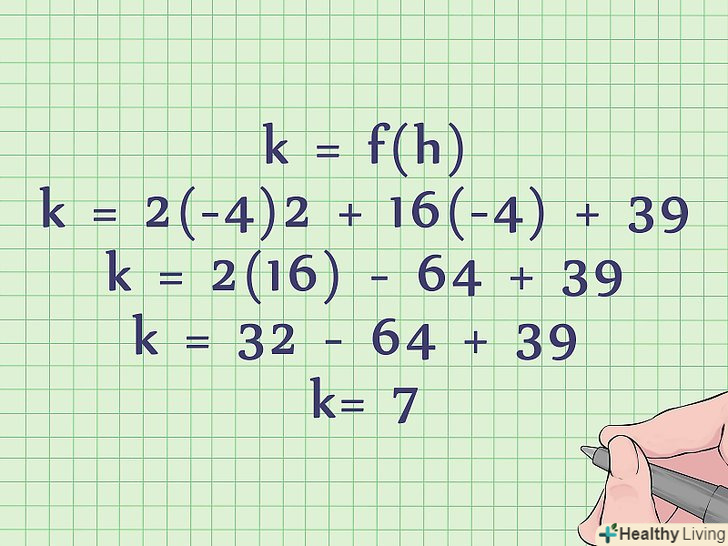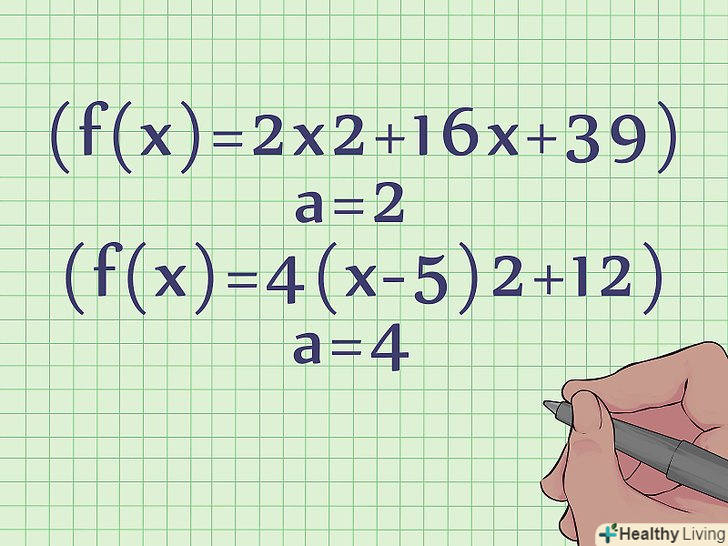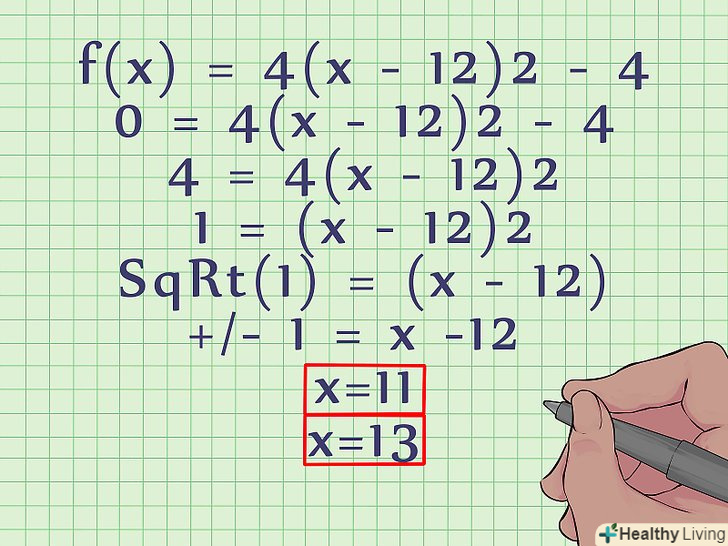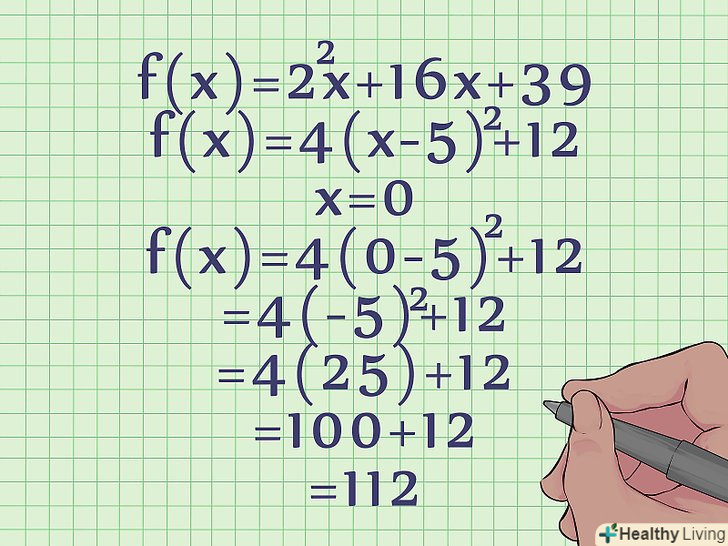1. Головна
    2. Математика
    3. Як зробити графік квадратного рівняння: 10 кроків

Як зробити графік квадратного рівняння: 10 кроків

Графік квадратного рівняння виду ax2 + bx + C або a(x - h)2 + k являє собою параболу (U-подібну криву). Для побудови графіка такого рівняння необхідно знайти вершину параболи, її напрямок і точки перетину з осями Х і Y. Якщо вам дано відносно просте квадратне рівняння, то ви можете підставити в нього різні значення «х», знайти відповідні значення «у» і побудувати графік.

Кроки

  1. Квадратне рівняння може бути записано в стандартному вигляді і в нестандартному вигляді.ви можете використовувати будь-який вид рівняння для побудови графіка квадратного рівняння (спосіб побудови трохи відрізняється). Як правило, в задачах квадратні рівняння наводяться в стандартному вигляді, але ця стаття розповість вам про обидва види запису квадратного рівняння.
    • Стандартний вигляд: f (x) = AX2 + bx + c, де A, b, c - дійсні числа і А ≈ 0.
      • Наприклад, два рівняння стандартного виду: f(x) = x2 + 2x + 1 і f (x) = 9x2 + 10x -8.
    • Нестандартний вигляд: f(x) = a (x - h)2 + k, де a, h, k - дійсні числа і А ≈ 0.
      • Наприклад, два рівняння нестандартного вигляду: f(x) = 9(x - 4)2 + 18 і -3(x - 5)2 + 1.
    • Для побудови графіка квадратного рівняння будь-якого виду спочатку потрібно знайти вершину параболи, яка має координати (h, k). Координати вершини параболи в рівняннях стандартного виду обчислюються за формулами: h = - b / 2a і k = f(h); координати вершини параболи в рівняннях нестандартного виду можна отримати безпосередньо з рівнянь.
  2. Для побудови графіка необхідно знайти чисельні значення коефіцієнтів a, b, c (або a, h, k).у більшості задач квадратні рівняння даються з чисельними значеннями коефіцієнтів.
    • Наприклад, у стандартному рівнянні f (x) = 2x2 +16x + 39 a = 2, b = 16, c = 39.
    • Наприклад, у нестандартному рівнянні f(x) = 4 (x - 5)2 + 12, a = 4, h = 5, k = 12.
  3. Обчисліть h в стандартному рівнянні (в нестандартному воно вже дано) за формулою: h = -b/2a.
    • У нашому прикладі стандартного рівняння f(x) = 2x2 +16x + 39 h = - b/2A = -16/2(2) = -4.
    • У нашому прикладі нестандартного рівняння f(x) = 4 (x - 5)2 + 12 h = 5.
  4. Обчисліть k в стандартному рівнянні (в нестандартному воно вже дано).Пам'ятайте, що k = f (h), тобто ви можете знайти k, підставивши у вихідне рівняння знайдене значення h замість «х».
    • Ви знайшли, що h = -4 (для стандартного рівняння). Для обчислення k підставте це значення замість " х»:
      • K = 2(-4)2 + 16(-4) + 39.
      • K = 2(16) - 64 + 39.
      • K = 32 - 64 + 39 =7
    • У нестандартному рівнянні k = 12.
  5. Нанесіть вершину з координатами (h, k) на координатній площині. H відкладається по осі X, а k - по осі Y. Вершина параболи є або найнижчою точкою (якщо парабола спрямована вгору), або найвищою точкою (якщо парабола спрямована вниз).
    • У нашому прикладі стандартного рівняння вершина має координати (-4, 7). Нанесіть цю точку на координатній площині.
    • У нашому прикладі нестандартного рівняння вершина має координати (5, 12). Нанесіть цю точку на координатній площині.
  6. Проведіть вісь симетрії параболи (не обов'язково).вісь симетрії проходить через вершину параболи паралельно осі Y (тобто строго вертикально). Вісь симетрії ділить параболу навпіл (тобто парабола дзеркально симетрична щодо цієї осі).
    • У нашому прикладі стандартного рівняння вісь симетрії є прямою, паралельною осі Y і проходить через точку (-4, 7). Хоча ця пряма і не є частиною самої параболи, вона дає уявлення про симетричність параболи.
  7. Визначте напрямок параболи-вгору або вниз.це дуже легко зробити. Якщо коефіцієнт "а «позитивний, то парабола спрямована вгору, а якщо коефіцієнт» а" негативний, то парабола спрямована вниз.
    • У нашому прикладі стандартного рівняння f (x) = 2x2 +16x + 39 парабола спрямована вгору, так як а = 2 (позитивний коефіцієнт).
    • У нашому прикладі нестандартного рівняння f(x) = 4 (x - 5)2 + 12 парабола також спрямована вгору, так як А = 4 (позитивний коефіцієнт).
  8. Якщо потрібно, знайдіть і нанесіть точки перетину з віссю х. ці точки дуже допоможуть вам при побудові параболи. Їх може бути дві, одна або жодної (якщо парабола спрямована вгору, а її вершина лежить вище осі Х, або якщо парабола спрямована вниз, а її вершина лежить нижче осі Х). Для обчислення координат точок перетину з віссю Х виконайте наступні дії:
    • Прирівняйте рівняння до нуля: f (х) = 0 і вирішіть його. Цей метод працює з простими квадратними рівняннями (особливо нестандартного вигляду), але може виявитися надзвичайно важким у випадку складних рівнянь. У нашому прикладі:
      • F(x) = 4(x - 12)2 - 4
      • 0 = 4(x - 12)2 - 4
      • 4 = 4(x - 12)2
      • 1 = (x - 12)2
      • √1 = (x - 12)
      • +/-1 = x -12. Точки перетину параболи з віссю Х мають координати (11,0) і (13,0).
    • Розкладіть квадратне рівняння стандартного виду на множники: ax2 + bx + c = (dx + e)(fx +g), де dx x fx = ax2, (dx x g + fx X e) = bx, e X G = c. потім прирівняйте кожен двучлен до 0 і знайдіть значення «х». Наприклад:
      • X2 + 2x + 1
      • = (x + 1)(x + 1)
      • У цьому випадку існує єдина точка перетину параболи з віссю Х з координатами (-1,0), тому що при х + 1= 0 х = -1.
    • Якщо ви не можете розкласти рівняння на множники, вирішіть його за допомогою формули для обчислення коренів квадратного рівняння: x = (-b +/- √(b2 - 4ac))/2a.
      • Наприклад: - 5x2 + 1x + 10.
      • X = (-1 +/- √(12 - 4(-5)(10)))/2(-5)
      • X = (-1 +/- √ (1 + 200))/-10
      • X = (-1 +/- √ (201))/-10
      • X = (-1 +/- 14,18)/-10
      • X = (13,18/-10) і (-15,18 / -10). Точки перетину параболи з віссю Х мають координати (-1,318,0) і (1,518,0).
      • У нашому прикладі рівняння стандартного вигляду 2x2 + 16x + 39:
      • X = (-16 +/- √(162 - 4(2)(39)))/2(2)
      • X = (-16 +/- √(256 - 312))/4
      • X = (-16 +/- √(-56)/-10
      • Так як витягти квадратний корінь з негативного числа не можна, то в цьому випадку парабола не перетинає вісь х.
    • Наприклад, парабола квадратного рівняння 2x2 + 16x + 39 перетинається з віссю Y в точці з координатами (0, 39), так як с = 39. Але це можна і обчислити:
      • F(x) = 2x2 + 16x + 39
      • F(x) = 2(0)2 + 16(0) + 39
      • F (x) = 39, тобто парабола даного квадратного рівняння перетинається з віссю Y в точці з координатами (0, 39).
    • У нашому прикладі рівняння нестандартного виду 4 (x - 5)2 + 12 точка перетину з віссю Y обчислюється наступним чином:
      • F(x) = 4(x - 5)2 + 12
      • F(x) = 4(0 - 5)2 + 12
      • F(x) = 4(-5)2 + 12
      • F(x) = 4(25) + 12
      • F (x) = 112, тобто парабола даного квадратного рівняння перетинається з віссю Y в точці з координатами (0, 112).
  10. Ви знайшли (і нанесли) вершину параболи, її напрямок і точки перетину з осями Х і Y. ви можете побудувати параболи по цих точках або знайти і нанести додаткові точки і тільки потім будувати параболу. Для цього підставте кілька значень "х «(по обидві сторони від вершини) у вихідне рівняння, щоб обчислити відповідні значення»у".
    • Повернемося до рівняння x2 + 2x + 1. Ви вже знаєте, то точкою перетину графіка цього рівняння з віссю Х є точка з координатами (-1,0). Якщо парабола має тільки одну точку перетину з віссю Х, то це вершина параболи, що лежить на осі Х.в цьому випадку однієї точки недостатньо для побудови правильної параболи. Тому знайдіть кілька додаткових точок.
      • Допустимо х = 0, х = 1, х = -2, х = -3.
      • Х = 0: f (x) = (0)2 + 2(0) + 1 = 1. Координати точки: (0,1).
      • Х = 1: f(x) = (1)2 + 2(1) + 1 = 4. Координати точки: (1,4).
      • Х = -2: f (x) = (-2)2 + 2(-2) + 1 = 1. Координати точки: (-2,1).
      • Х = -3: f (x) = (-3)2 + 2(-3) + 1 = 4. Координати точки: (-3,4).
      • Нанесіть ці точки на координатній площині і побудуйте параболу (з'єднайте точки U-подібної кривої). Зверніть увагу, що парабола абсолютно симетрична-будь-яку точку на одній гілці параболи можна дзеркально відобразити (щодо осі симетрії) на іншій гілці параболи. Цим Ви заощадите час, так як вам не потрібно обчислювати координати точок на обох гілках параболи.

Поради

  • Округляйте дробові числа (якщо це вимога викладача) – так ви побудуєте правильну параболу.
  • Якщо в f(x) = AX2 + bx + c коефіцієнти b або c дорівнюють нулю, то членів з цими коефіцієнтами в рівнянні немає. Наприклад, 12x2 + 0x + 6 перетворюється на 12x2 + 6, оскільки 0x дорівнює 0.

Джерела

  1. Http://jwilson.coe.uga.edu/EMT668/EMAT6680.Folders/Barron /unit/Lesson%206/6.html
  2. Http://www.analyzemath.com/quadraticg/quadraticg.htm
  3. Http://www.mathsisfun.com/algebra/quadratic-equation-graphing.html
  4. Http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut34_quadfun .htm

Ще почитати: