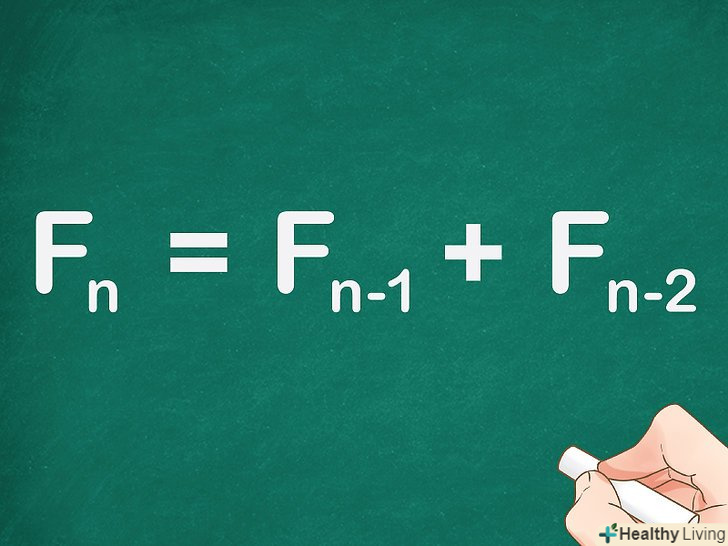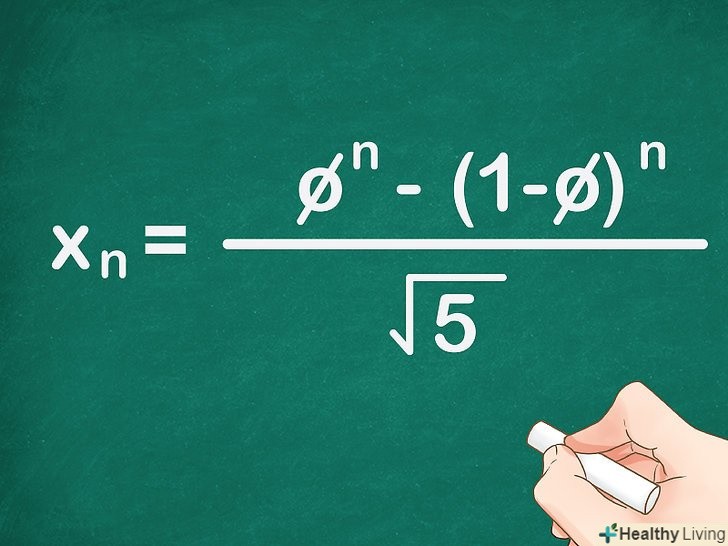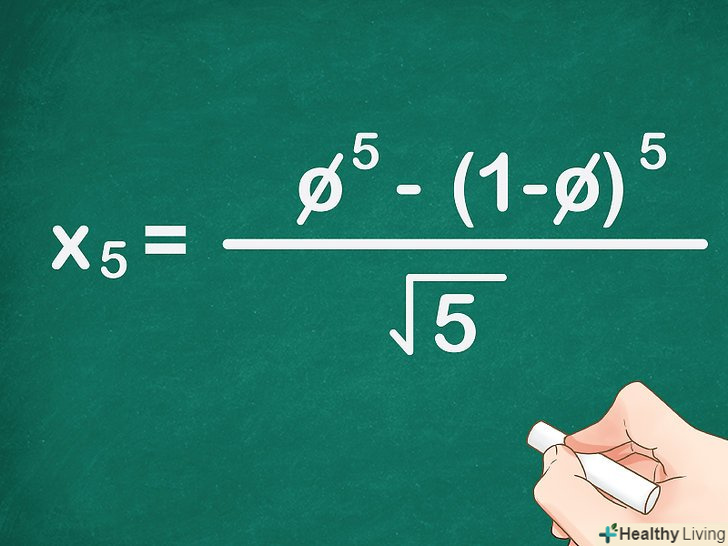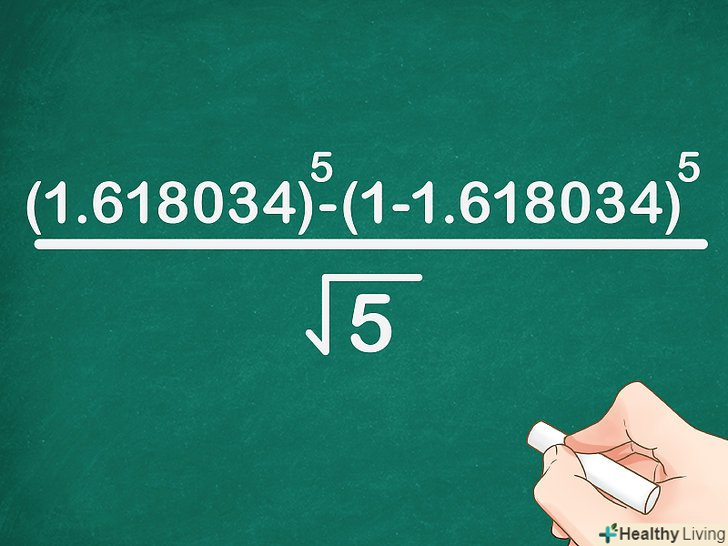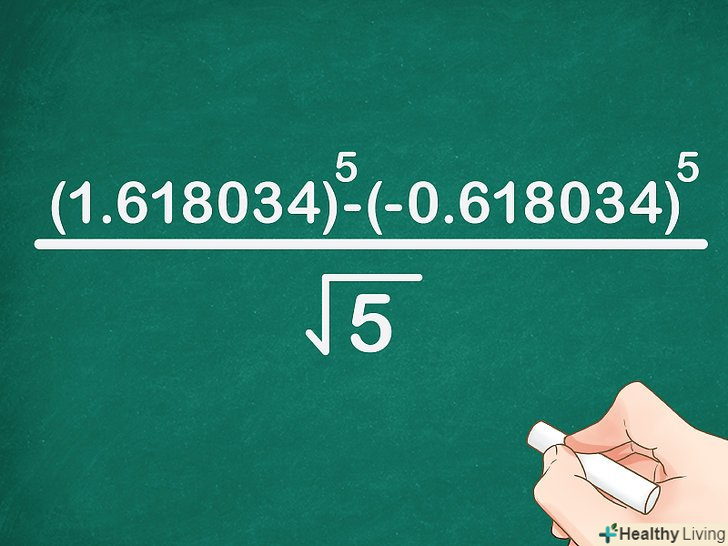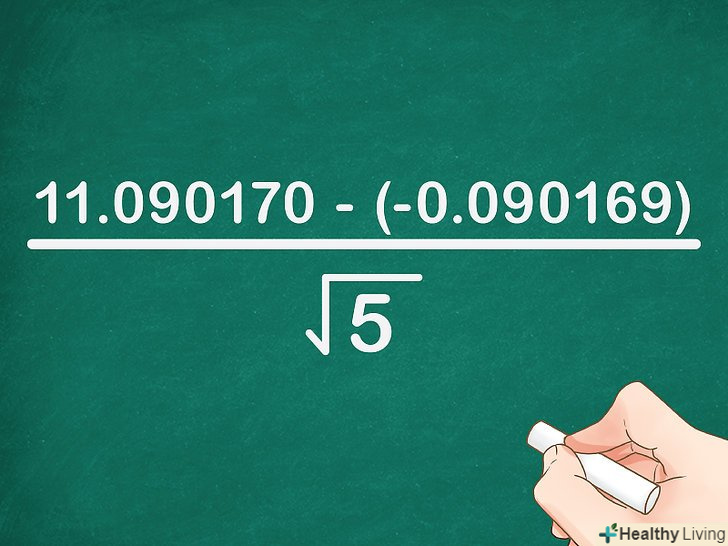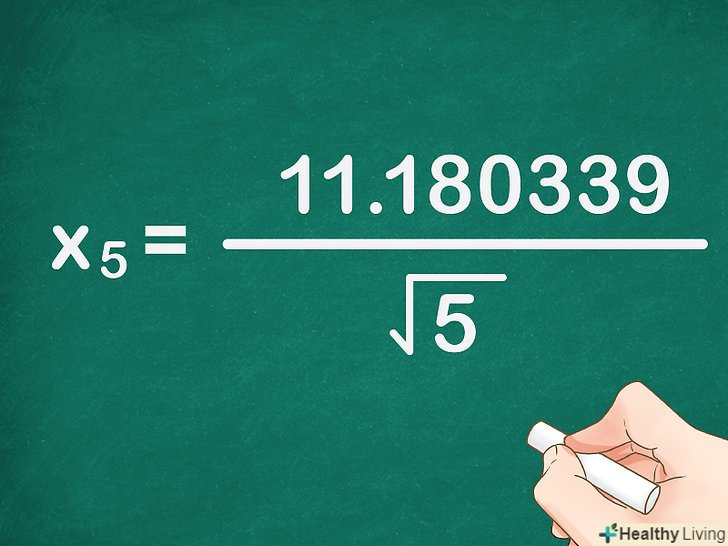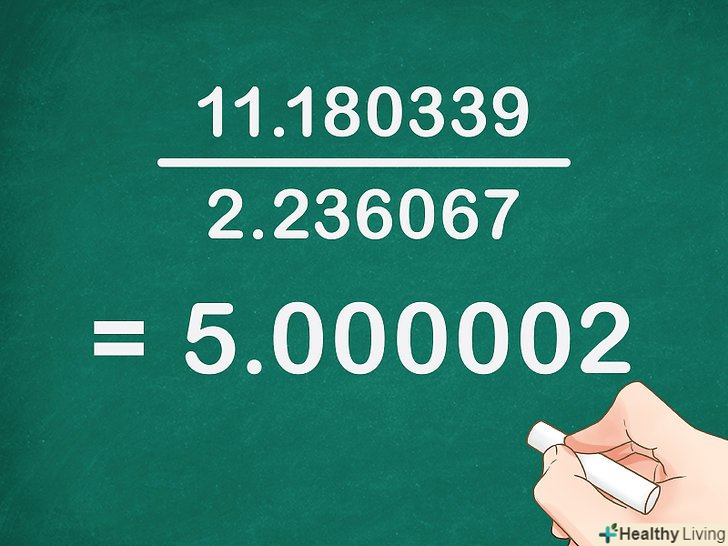1. Головна
    2. Математика
    3. Як розрахувати послідовність Фібоначчі

Як розрахувати послідовність Фібоначчі

Послідовність Фібоначчі-це ряд чисел, в якому кожне наступне число дорівнює сумі двох попередніх чисел. Числові послідовності часто зустрічаються в природі і мистецтві у вигляді спіралей і «золотого перетину». Найпростіший спосіб обчислити послідовність Фібоначчі-це створити таблицю, але такий метод не застосуємо до великих послідовностей. Наприклад, якщо потрібно визначити 100-й член послідовності, краще скористатися формулою Біне.

Метод1 З 2:
Таблиця

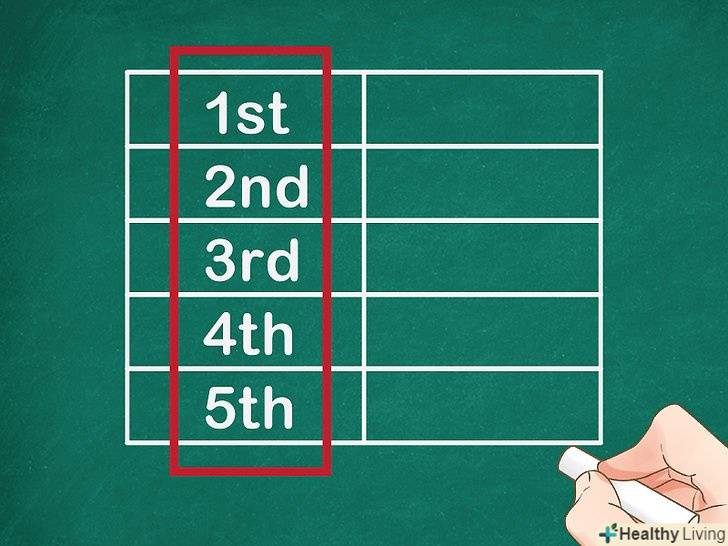
  1. Намалюйте таблицю з двома стовпцями.кількість рядків таблиці залежить від кількості чисел послідовності Фібоначчі, які потрібно знайти.
    • Наприклад, якщо потрібно знайти п'яте число послідовності, намалюйте таблицю з п'ятьма рядками.
    • Використовуючи таблицю, не можна знайти деяке випадкове число без обчислення всіх попередніх чисел. Наприклад, якщо потрібно знайти 100-е число послідовності, потрібно обчислити всі числа: від першого до 99-ого. Тому таблиця може бути застосована тільки для знаходження перших чисел послідовності.
  2. У лівому стовпці напишіть порядкові номери членів послідовності.тобто напишіть цифри по порядку, починаючи з одиниці.
    • Такі цифри визначають порядкові номери членів (чисел) послідовності Фібоначчі.
    • Наприклад, якщо потрібно знайти п'яте число послідовності, в лівій колонці напишіть наступні цифри: 1, 2, 3, 4, 5. Тобто потрібно знайти з першого по п'яте число послідовності.
  3. У першому рядку правої колонки напишіть 1.це перше число (член) послідовності Фібоначчі.
    • Майте на увазі, що послідовність Фібоначчі завжди починається з 1. Якщо послідовність починається з іншого числа, ви неправильно вирахували всі числа аж до першого.
  4. До першого члена (1) Додайте 0.вийде друге число послідовності.
    • Запам'ятайте: щоб знайти будь-яке число послідовності Фібоначчі, просто складіть два попередніх числа.
    • Щоб створити послідовність, не забудьте про 0, який стоїть перед 1 (першим членом), тому 1 + 0 = 1.
  5. Складіть перший (1) і другий (1) члени.вийде третє число послідовності.
    • 1 + 1 = 2. Третій член дорівнює 2.
  6. Складіть другий (1) і третій (2) члени, щоб отримати четверте число послідовності.
    • 1 + 2 = 3. Четвертий член дорівнює 3.
  7. Складіть третій (2) і четвертий (3) члени.вийде п'яте число послідовності.
    • 2 + 3 = 5. П'ятий член дорівнює 5.
  8. Складіть два попередніх числа, щоб знайти будь-яке число послідовності Фібоначчі. цей метод заснований на формулі: Fn=Fn−1+Fn−2{\displaystyle F_{n}=F_{n-1}+F_{n-2}}.[1] ця формула не є замкнутою, тому за допомогою цієї формули не можна знайти будь-який член послідовності без обчислення всіх попередніх чисел.

Метод2 З 2:
Формула Біне і золотий перетин

  1. Запишіть формулу: Xn{\displaystyle x_{n}}=. У цій формулі Xn{\displaystyle x_{n}} – шуканий член послідовності, – порядковий номер члена, – золотий переріз.[2]
    • Це замкнута формула, тому по ній можна знайти будь-який член послідовності без обчислення всіх попередніх чисел.
    • Це спрощена формула, отримана з формули Біне для чисел Фібоначчі.[3]
    • У формулі присутній золотий перетин (), тому що відношення будь-яких двох послідовних чисел послідовності Фібоначчі дуже схоже на золоте відношення.[4]
  2. У формулу підставте порядковий номер числа (замістьN{\displaystyle n}). – це порядковий номер будь-якого потрібного члена послідовності.
    • Наприклад, якщо потрібно знайти п'яте число послідовності, в формулу підставте 5. Формула запишеться так:X5{\displaystyle x_{5}}=.
  3. У формулу підставте золотий перетин. Золотий Перетин приблизно дорівнює 1,618034; підставте в формулу це число.[5]
    • Наприклад, якщо потрібно знайти п'яте число послідовності, формула запишеться так:X5{\displaystyle x_{5}}=.
  4. Обчисліть вираз у дужках. не забувайте про правильний порядок виконання математичних операцій, в якому вираз в дужках обчислюється в першу чергу:1−1,618034=−0,618034{\displaystyle 1-1,618034=-0,618034}.
    • У нашому прикладі формула запишеться так:X5{\displaystyle x_{5}}=.
  5. Зведіть числа в ступені.зведіть у відповідні ступені два числа, які знаходяться в чисельнику.
    • У нашому прикладі:1,6180345=11,090170{\displaystyle 1,618034^{5}=11,090170}; . Формула запишеться так: X5=11,090170−(−0,090169)5{\displaystyle x_{5}={\frac {11,090170-(-0,090169)}{\sqrt {5}}}}.
  6. Відніміть два числа. Перед тим як приступити до поділу, відніміть числа, які знаходяться в чисельнику.
    • У нашому прикладі:11,090170−(−0,090169)=11,180339{\displaystyle 11,090170-(-0,090169)=11,180339}. Формула запишеться так: X5{\displaystyle x_{5}}=.
  7. Отриманий результат розділіть на квадратний корінь з 5. квадратний корінь з 5 приблизно дорівнює 2,236067.
    • У нашому прикладі:11,1803392,236067=5,000002{\displaystyle {\frac {11,180339}{2,236067}}=5,000002}.
  8. Отриманий результат округлите до найближчого цілого числа.останній результат буде десятковим дробом, який близький до цілого числа. Таке ціле число являє собою число послідовності Фібоначчі.
    • Якщо в обчисленнях використовувати неокруглені числа, Ви отримаєте ціле число. Працювати з округленими числами набагато легше, але в цьому випадку ви отримаєте десятковий дріб.[6]
    • У нашому прикладі ви отримали десятковий дріб 5,000002. Округліть її до найближчого цілого числа і отримаєте п'яте число послідовності Фібоначчі, яке дорівнює 5.

Джерела

  1. ↑ Http://mathworld.wolfram.com/FibonacciNumber.html
  2. ↑ Https://www.mathsisfun.com/numbers/fibonacci-sequence.html
  3. ↑ Http://mathworld.wolfram.com/FibonacciNumber.html
  4. ↑ Https://www.mathsisfun.com/numbers/fibonacci-sequence.html
  5. ↑ Https://www.mathsisfun.com/numbers/fibonacci-sequence.html
  6. ↑ Https://www.mathsisfun.com/numbers/fibonacci-sequence.html

Ще почитати: