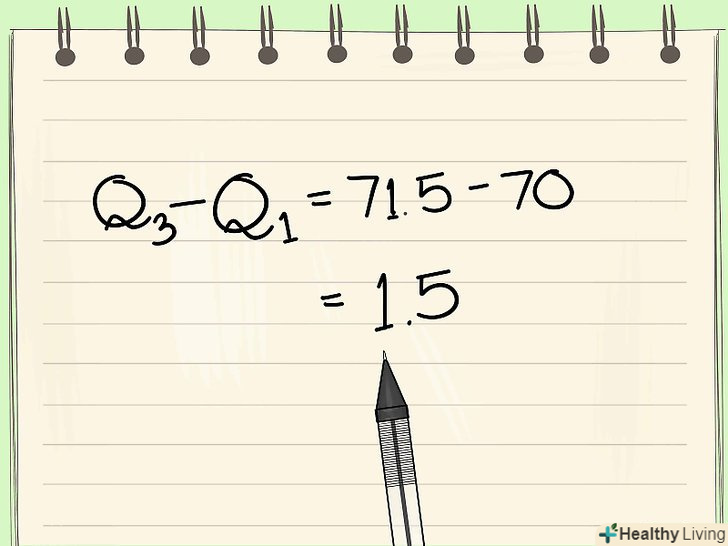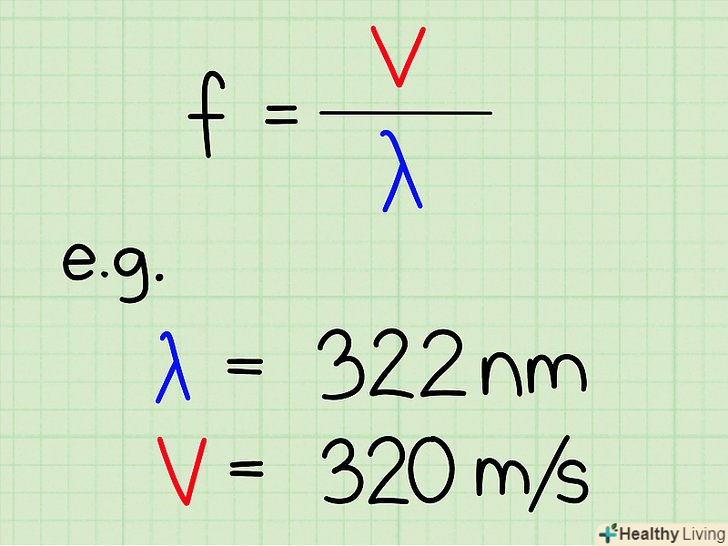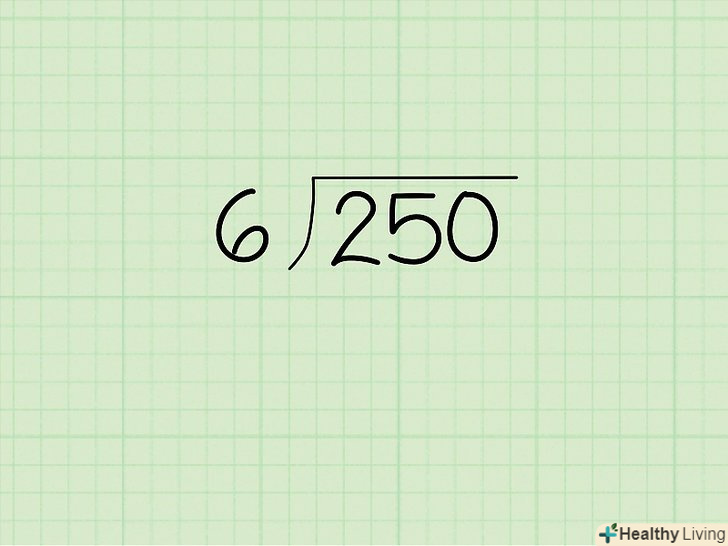Як обчислити викиди: 10 кроків (з ілюстраціями)

Навчіться розпізнавати потенційний викид. перед тим, як виключати виділяються значення з набору даних, слід визначити потенційні викиди. Викиди є значеннями, які сильно відрізняються від більшості значень у наборі даних; іншими словами, викиди лежать поза тенденцією більшості значень. Це легко виявити в таблицях значень або (особливо) на графіках. Якщо значення в наборі даних нанести на графік, то викиди будуть лежати далеко від більшості інших значень. Якщо, наприклад, більшість значень лягають на пряму, то викиди лежать по обидва боки від такої прямої.

• Наприклад, розглянемо набір даних, що представляє температури 12 різних об'єктів в кімнаті. Якщо 11 об'єктів мають температуру приблизно 70 градусів, але дванадцятий об'єкт (можливо, піч) має температуру 300 градусів, то швидкий перегляд значень може показати, що піч є ймовірним викидом.

Упорядкуйте дані по зростанню.перший крок при визначенні викидів-це обчислення медіани набору даних. Це завдання значно спрощується, якщо значення в наборі даних розташовані за зростанням (від меншого до більшого).

• Продовжуючи наведений вище приклад, розглянемо наступний набір даних, що представляє температури декількох об'єктів: {71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}. Цей набір повинен бути впорядкований наступним чином: {69, 69, 70, 70, 70, 70, 71, 71, 71, 72, 73, 300}.

Обчисліть медіану набору даних. медіана набору даних-це величина, що знаходиться в середині набору даних. Якщо набір даних містить непарну кількість значень, то медіана-це значення, до якого і після якого розташована однакова кількість значень в наборі даних. Але якщо набір даних містить парне число значень, то потрібно знайти середнє арифметичне двох середніх значень. Зверніть увагу, що при обчисленні викидів медіана, як правило, позначається як Q2, так як вона лежить між Q1 і Q3 – нижнім і верхнім квартилями, які ми визначимо пізніше.

• Не бійтеся працювати з наборами даних, в яких парна кількість значень-середнім арифметичним двох середніх значень буде число, якого немає в наборі даних; це нормально. Але якщо два середні значення - це одне і те ж число, то середнє арифметичне дорівнює цьому числу; це теж в порядку речей.
• У наведеному вище прикладі середні 2 значення-це 70 і 71, так що медіана дорівнює ((70+71)/2) = 70,5.

Обчисліть нижній квартиль. ця величина, що позначається як Q1, нижче якої лежить 25% значень з набору даних. Іншими словами, це половина значень, розташованих до медіани. Якщо до медіани лежить парна кількість значень з набору даних, потрібно знайти середнє арифметичне двох середніх значень, щоб обчислити Q1 (це аналогічно обчисленню медіани).

• У нашому прикладі 6 значень розташовані після медіани і 6 значень – до неї. Це означає, що для обчислення нижнього квартиля нам потрібно знайти середнє арифметичне двох середніх значень з шести значень, що лежать до медіани. Тут середні значення рівні 70 і 70. Таким чином, Q1 = ((70 + 70)/2) = 70.

Обчисліть верхній квартиль. ця величина, що позначається як Q3, вище якої лежить 25% значень з набору даних. Процес обчислення Q3 аналогічний процесу обчислення Q1, але тут розглядаються значення, розташовані після медіани.

• У наведеному вище прикладі два середніх значення з шести значень, що лежать після медіани, рівні 71 і 72. Таким чином, Q3 = ((71 + 72)/2) = 71,5.

Обчисліть міжквартильний діапазон.обчисливши Q1 і Q3, необхідно знайти відстань між цими величинами. Для цього відніміть Q1 з Q3. Значення міжквартильного діапазону вкрай важливо для визначення меж значень, які не є викидами.

• У нашому прикладі Q1 = 70, а Q3 = 71,5. Міжквартильний діапазон дорівнює 71,5 - 70 = 1,5.
• Зверніть увагу, що це може бути застосовано і до негативних значень Q1 і Q3. Наприклад, якщо Q1 = -70, то міжквартильний діапазон дорівнює 71,5 - (-70) = 141,5.

Знайдіть "внутрішні межі" значень у наборі даних.викиди визначаються через аналіз значень-чи потрапляють вони чи ні в межі так званих "внутрішніх кордонів»і "зовнішніх кордонів". Значення, що лежить поза "внутрішніми кордонами«, класифікується як» незначний викид«, в той час як значення, що знаходиться за» зовнішніми кордонами«, класифікується як»значний викид". Щоб знайти внутрішні межі, необхідно помножити міжквартильний діапазон на 1,5; результат потрібно додати до Q3 і відняти з Q1. Два знайдених числа є внутрішніми межами набору даних.

• У нашому прикладі міжквартильний діапазон дорівнює (71,5-70) = 1,5. Далі: 1,5 * 1,5 = 2,25. Це число потрібно додати до Q3 і відняти його з Q1, щоб знайти внутрішні кордони:
  • 71,5 + 2,25 = 73,75
  • 70 - 2,25 = 67,75
  • Таким чином, внутрішні межі рівні 67,75 і 73,75.
• У нашому прикладі тільки температура печі-300 градусів-лежить поза цими межами і може вважатися незначним викидом. Але не поспішайте з висновками-нам належить визначити, чи є ця температура значним викидом.
  

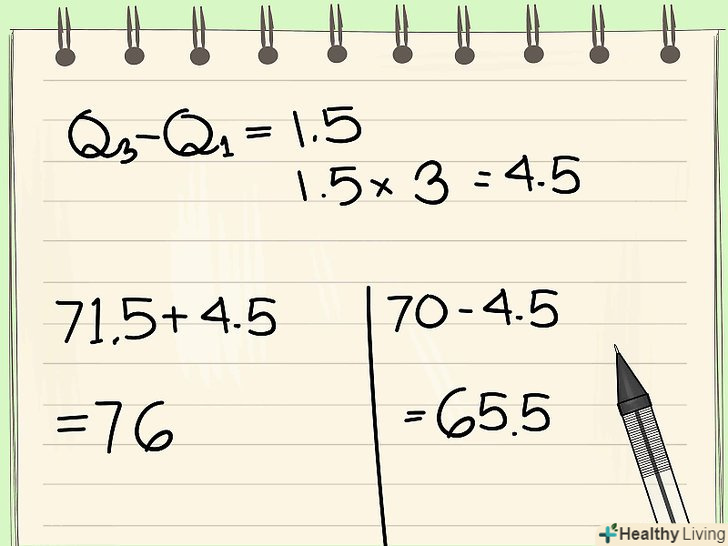
Знайдіть "зовнішні межі" набору даних. це робиться таким же чином, як для внутрішніх кордонів, за винятком того, що міжквартильний діапазон множиться на 3, а не на 1,5. Результат потрібно додати до Q3 і відняти з Q1. Два знайдених числа є зовнішніми межами набору даних.

• У нашому прикладі помножте міжквартильний діапазон на 3: 1,5 * 3 = 4,5. Обчисліть зовнішні межі:
  • 71,5 + 4,5 = 76
  • 70 - 4,5 = 65,5
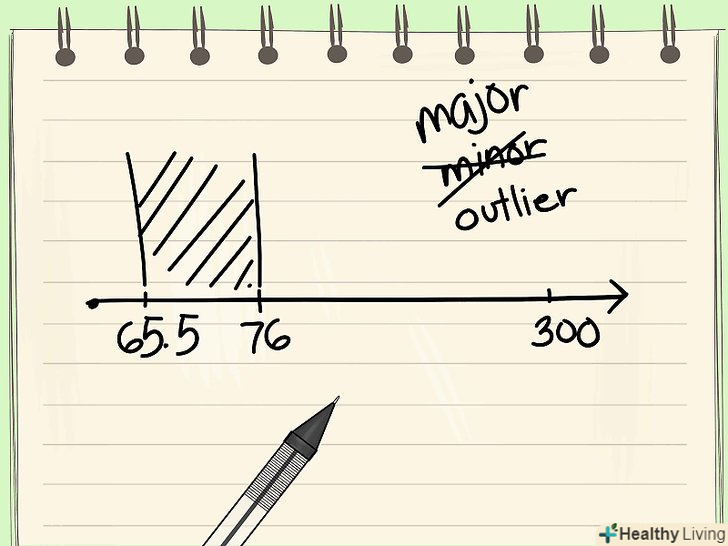
  • Таким чином, зовнішні межі рівні 65,5 і 76.
• Будь-які значення, які лежать за межами зовнішніх кордонів, вважаються значними викидами. У нашому прикладі температура печі - 300 градусів-вважається значним викидом.
  

Скористайтеся якісною оцінкою для визначення того, чи потрібно виключати викиди з набору даних.метод, описаний вище, дозволяє визначити, чи є деякі значення викидами (незначними або значними). Тим не менш, не помиляйтеся – значення, яке класифікується як викид, є тільки «кандидатом» на виключення, тобто ви не зобов'язані його виключати. Причина виникнення викиду-це основний фактор, що впливає на рішення про виключення викиду. Як правило, викиди, які виникають через помилку (у вимірах, записах і так далі), виключаються. З іншого боку, викиди, пов'язані не з помилками, а з новою інформацією або тенденцією, як правило, залишають в наборі даних.

• Не менш важливо оцінити вплив викидів на медіану набору даних (чи спотворюють вони її чи ні). Це особливо важливо в тому випадку, коли ви робите висновки на основі медіани набору даних.
• У нашому прикладі вкрай малоймовірно, що піч нагріється до температури 300 градусів (якщо тільки не враховувати природні аномалії). Тому можна зробити висновок (з високою часткою впевненості), що така температура – це помилка вимірювань, яку потрібно виключити з набору даних. Більш того, якщо ви не виключите викид, медіана набору даних буде дорівнює (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73 + 300)/12 = 89,67 градусів, але якщо ви виключите викид, медіана буде дорівнює (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73)/11 = 70,55 градусів.
  • Викиди – це, як правило, результат людських помилок, тому викиди необхідно виключати з наборів даних.