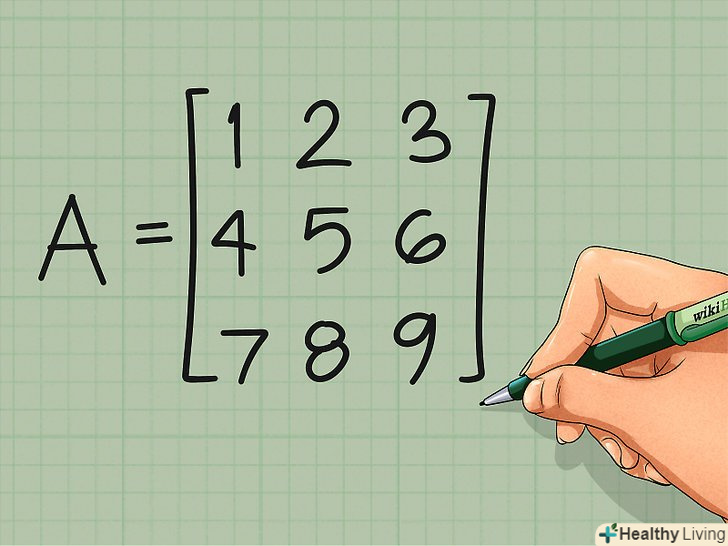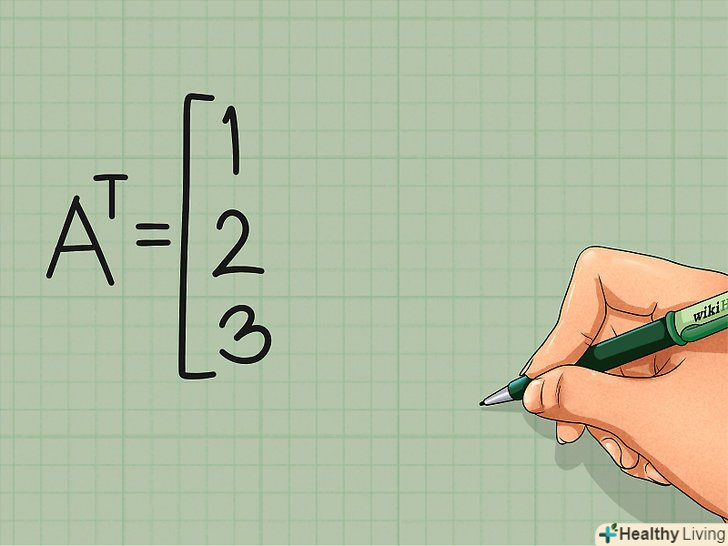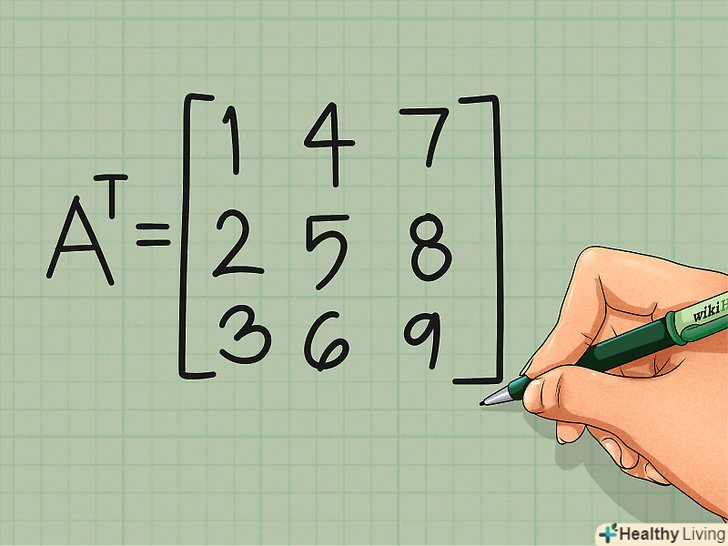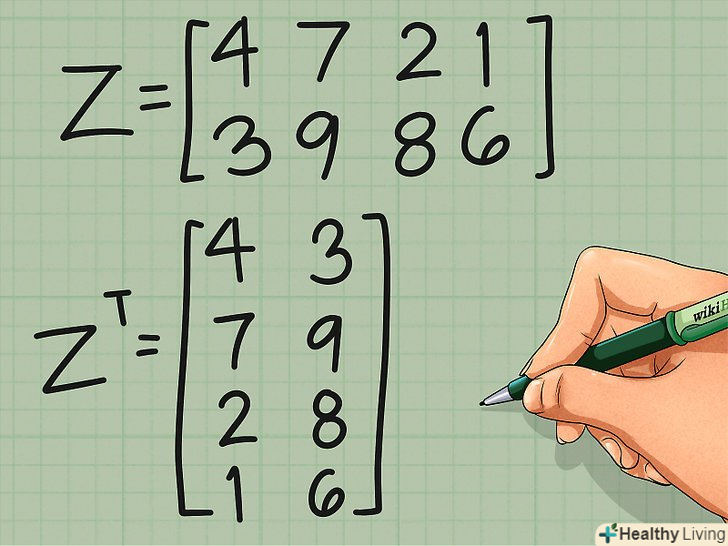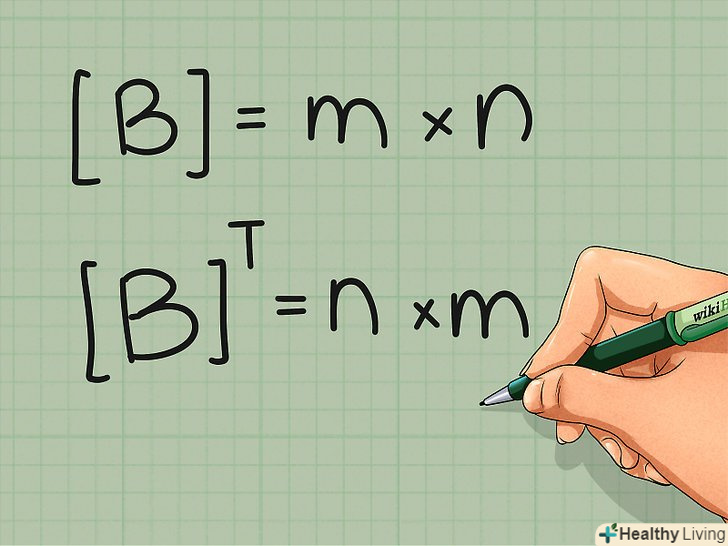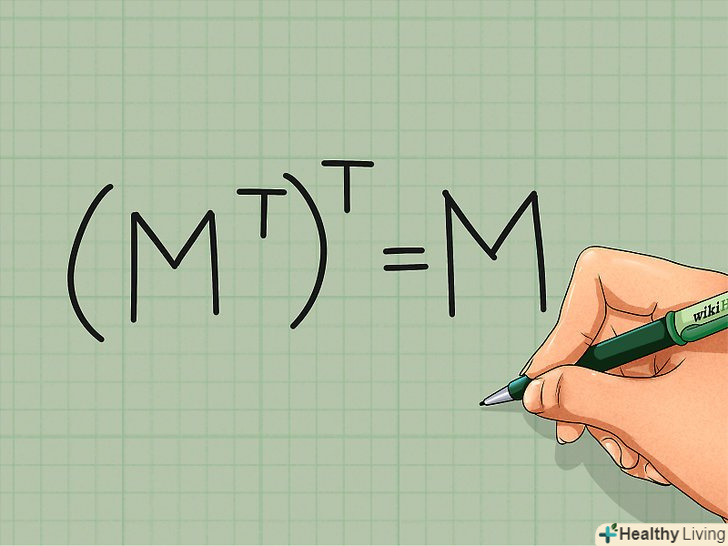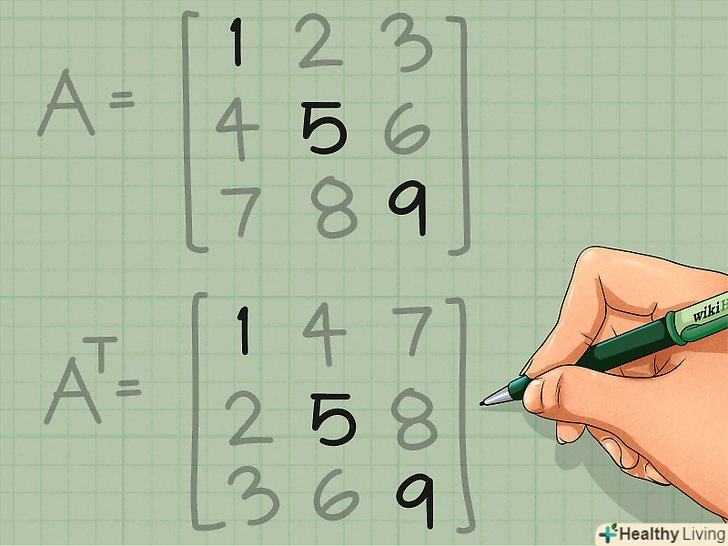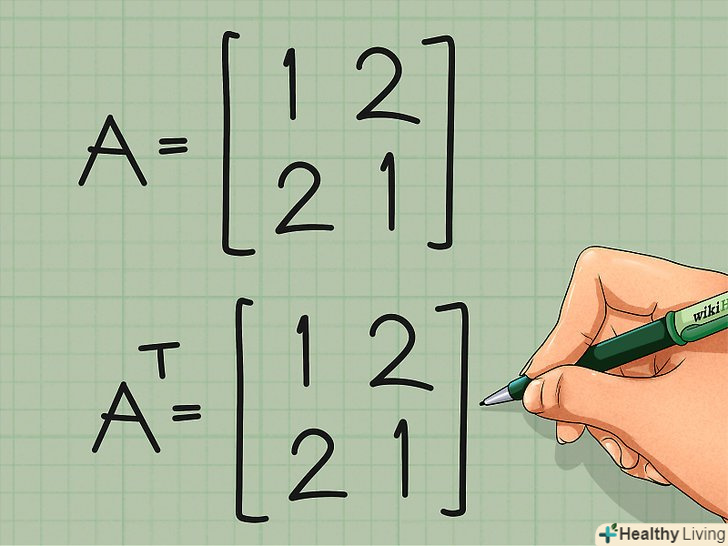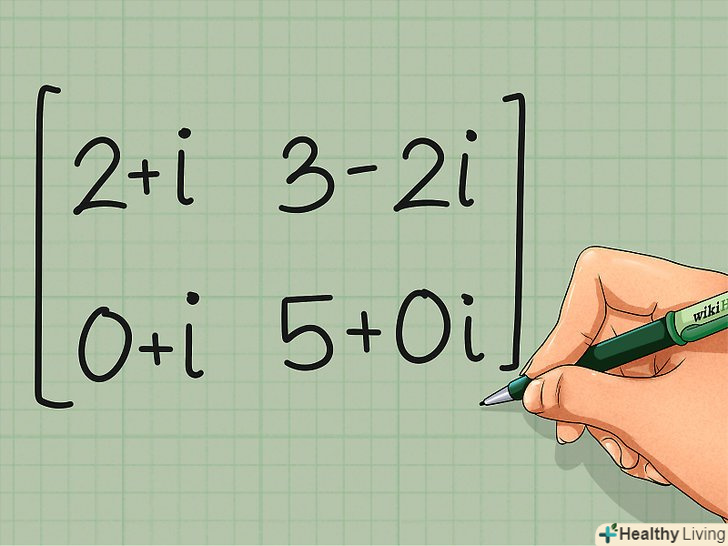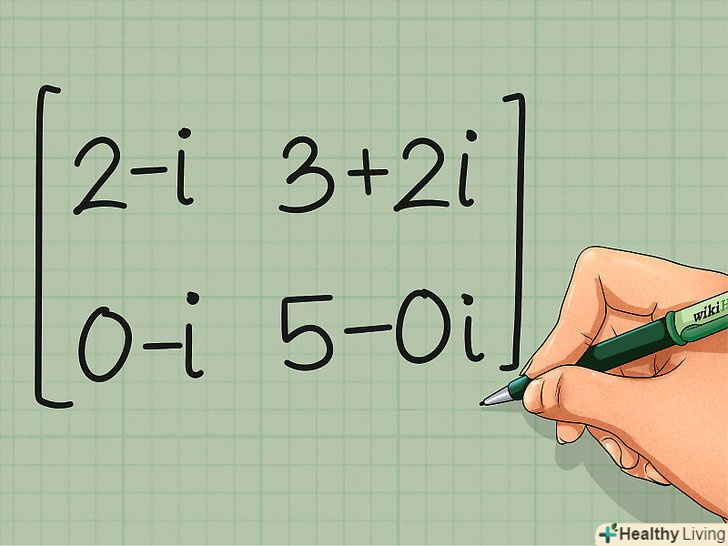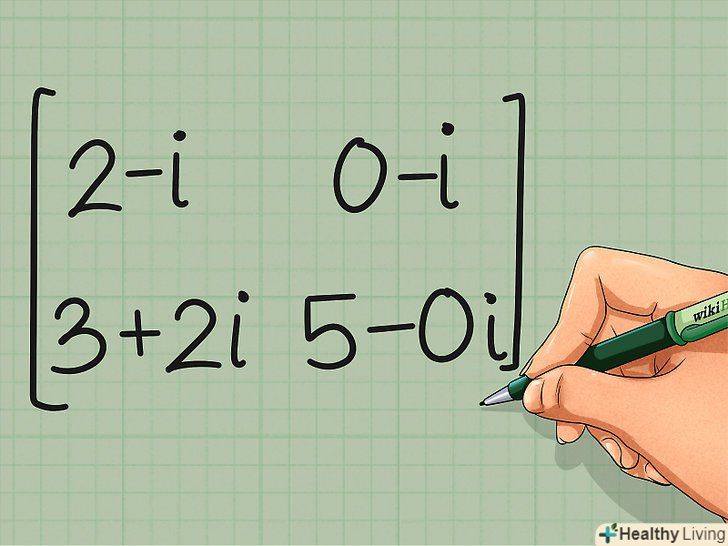Якщо ви навчитеся транспонувати матриці, то краще зрозумієте їх структуру. Можливо, ви вже знаєте про квадратних матрицях і про їх симетрії, що допоможе вам освоїти транспонування. Крім іншого, транспонування допомагає переводити вектори в матричну форму і знаходити векторні твори.[1] при роботі з комплексними матрицями ермітово-пов'язані (сполучено-транспоновані) матриці допомагають вирішити найрізноманітніші завдання.
Кроки
Частина1З 3:
Транспонування матриці
Частина1З 3:
 Візьміть будь-яку матрицю. можна транспонувати будь-яку матрицю, незалежно від кількості рядків і стовпців. Найбільш часто доводиться транспонувати квадратні матриці, які мають однакову кількість рядків і стовпців, тому для простоти розглянемо як приклад таку матрицю:[2]
Візьміть будь-яку матрицю. можна транспонувати будь-яку матрицю, незалежно від кількості рядків і стовпців. Найбільш часто доводиться транспонувати квадратні матриці, які мають однакову кількість рядків і стовпців, тому для простоти розглянемо як приклад таку матрицю:[2]- МатрицяA =
1 2 3
4 5 6
7 8 9
- МатрицяA =
 Уявіть перший рядок прямої матриці у вигляді першого стовпця транспонованої матриці. просто запишіть перший рядок у вигляді стовпця:
Уявіть перший рядок прямої матриці у вигляді першого стовпця транспонованої матриці. просто запишіть перший рядок у вигляді стовпця:- Транспонована матриця = at
- Перший стовпець матриці At:
1
2
3
 Виконайте те ж саме з іншими рядками.другий рядок вихідної матриці стане другим стовпцем транспонованої матриці. Переведіть всі рядки в стовпці:
Виконайте те ж саме з іншими рядками.другий рядок вихідної матриці стане другим стовпцем транспонованої матриці. Переведіть всі рядки в стовпці:- AT =
1 4 7
2 5 8
3 6 9
- AT =
 Спробуйте транспонувати неквадратну матрицю.точно таким же чином можна транспонувати будь-яку прямокутну матрицю. Просто запишіть перший рядок у вигляді першого стовпця, другий рядок — у вигляді другого стовпця, і так далі. У наведеному нижче прикладі кожен рядок вихідної матриці позначена своїм кольором, щоб було зрозуміліше, як вона перетворюється при транспонуванні:
Спробуйте транспонувати неквадратну матрицю.точно таким же чином можна транспонувати будь-яку прямокутну матрицю. Просто запишіть перший рядок у вигляді першого стовпця, другий рядок — у вигляді другого стовпця, і так далі. У наведеному нижче прикладі кожен рядок вихідної матриці позначена своїм кольором, щоб було зрозуміліше, як вона перетворюється при транспонуванні:- МатрицяZ =
4 7 2 1
3 9 8 6 - МатрицяZt =
4 3
7 9
2 8
1 6
- МатрицяZ =
 Висловимо транспонування у вигляді математичного запису.хоча ідея транспонування дуже проста, краще все ж записати її у вигляді суворої формули. При матричної записи не потрібні будь-які спеціальні терміни:
Висловимо транспонування у вигляді математичного запису.хоча ідея транспонування дуже проста, краще все ж записати її у вигляді суворої формули. При матричної записи не потрібні будь-які спеціальні терміни:- Припустимо, дана матриця B, що складається зm x n елементів (m рядків і n стовпців), тоді транспонована матриця BT являє собою набір з n x m елементів (n рядків і m стовпців).[3]
- Для кожного елемента bxy (рядок x і стовпець y) матриці B в матриці BT існує еквівалентний йому елемент byx (рядок y і стовпець x).
Частина2З 3:
Властивості транспонування
Частина2З 3:
 (MT)T = M. після подвійного транспонування виходить вихідна матриця.[4] це досить очевидно, так як при повторному транспонуванні ви знову міняєте рядки і стовпці, в результаті чого виходить первісна матриця.
(MT)T = M. після подвійного транспонування виходить вихідна матриця.[4] це досить очевидно, так як при повторному транспонуванні ви знову міняєте рядки і стовпці, в результаті чого виходить первісна матриця. Дзеркально відобразіть матрицю відносно головної діагоналі.квадратні матриці можна "перевертати" щодо головної діагоналі. При цьому елементи уздовж головної діагоналі (від a11 до нижнього правого кута матриці) залишаються на місці, а інші елементи переміщаються по інший бік цієї діагоналі і залишаються на тій же відстані від неї.
Дзеркально відобразіть матрицю відносно головної діагоналі.квадратні матриці можна "перевертати" щодо головної діагоналі. При цьому елементи уздовж головної діагоналі (від a11 до нижнього правого кута матриці) залишаються на місці, а інші елементи переміщаються по інший бік цієї діагоналі і залишаються на тій же відстані від неї.- Якщо вам складно уявити даний метод, візьміть аркуш паперу і намалюйте матрицю 4x4. Потім переставте її бічні елементи щодо головної діагоналі. Простежте при цьому за елементами a14 і a41. При транспонуванні вони повинні помінятися місцями, як і інші пари бічних елементів.
 Транспонуйте симетричну матрицю. елементи такої матриці симетричні щодо головної діагоналі. Якщо виконати описану вище операцію і" перевернути " симетричну матрицю, вона не зміниться. Всі елементи поміняються на аналогічні.[5] фактично, це стандартний спосіб визначити, чи симетрична та чи інша матриця. Якщо виконується рівність A = At, значить, матриця A симетрична.
Транспонуйте симетричну матрицю. елементи такої матриці симетричні щодо головної діагоналі. Якщо виконати описану вище операцію і" перевернути " симетричну матрицю, вона не зміниться. Всі елементи поміняються на аналогічні.[5] фактично, це стандартний спосіб визначити, чи симетрична та чи інша матриця. Якщо виконується рівність A = At, значить, матриця A симетрична.
Частина3З 3:
Эрмитово- сполучена матриця з комплексними елементами
Частина3З 3:
 Розглянемо комплексну матрицю. елементи комплексної матриці складаються з дійсної і уявної частини. Таку матрицю також можна транспонувати, хоча в більшості практичних застосувань використовують сполучено-транспоновані, або ермітово-пов'язані матриці.[6]
Розглянемо комплексну матрицю. елементи комплексної матриці складаються з дійсної і уявної частини. Таку матрицю також можна транспонувати, хоча в більшості практичних застосувань використовують сполучено-транспоновані, або ермітово-пов'язані матриці.[6]- Нехай дана матриця c =
2+i 3-2i
0 + i 5 + 0i
- Нехай дана матриця c =
 Замінимо елементи комплексно-Сполученими числами. При операції комплексного сполучення дійсна частина залишається такою ж, а уявна частина змінює свій знак на зворотний. Виконаємо цю операцію з усіма чотирма елементами матриці.
Замінимо елементи комплексно-Сполученими числами. При операції комплексного сполучення дійсна частина залишається такою ж, а уявна частина змінює свій знак на зворотний. Виконаємо цю операцію з усіма чотирма елементами матриці.- Знайдемо комплексно-сполучену матрицю c* =
2-i 3 + 2i
0 - i 5-0i
- Знайдемо комплексно-сполучену матрицю c* =
 Транспонуємо отриману матрицю.візьмемо знайдену комплексно-сполучену матрицю і просто транспонуємо її. В результаті у нас вийде сполучено-транспонована (ермітово-сполучена) матриця.
Транспонуємо отриману матрицю.візьмемо знайдену комплексно-сполучену матрицю і просто транспонуємо її. В результаті у нас вийде сполучено-транспонована (ермітово-сполучена) матриця.- Сполучено-транспонована матриця cH =
2 - i 0 - i
3 + 2i 5-0i
- Сполучено-транспонована матриця cH =
Поради
- У цій статті транспонована матриця щодо матриці А позначається як at. Зустрічається також позначення A' або Ã.[7]
- У даній статті ермітово-сполучена матриця щодо матриці А позначається як ah - це загальноприйняте позначення в лінійній алгебрі. У квантовій механіці часто використовують позначення a†. Іноді ермітово-сполучену матрицю записують у вигляді A*, проте такого позначення краще уникати, так як воно використовується також для запису комплексно-сполученої матриці.[8]
Джерела
- ↑ Http://mathforum.org/library/drmath/view/71949.html
- ↑ Https://chortle.ccsu.edu/VectorLessons/vmch13/vmch13_14.html
- ↑ Http://www.mathcentre.ac.uk/resources/uploaded/sigma-matrices2-2009-1.pdf
- ↑ Https://www.khanacademy.org/math/linear-algebra/matrix_transformations/matrix_transpose/v/linear-algebra-transpose-of-a-matrix
- ↑ Http://www.mathcentre.ac.uk/resources/uploaded/sigma-matrices2-2009-1.pdf
- ↑ Http://mathworld.wolfram.com/ConjugateTranspose.html
- ↑ Http://mathworld.wolfram.com/Transpose.html
- ↑ Http://mathworld.wolfram.com/ConjugateTranspose.html