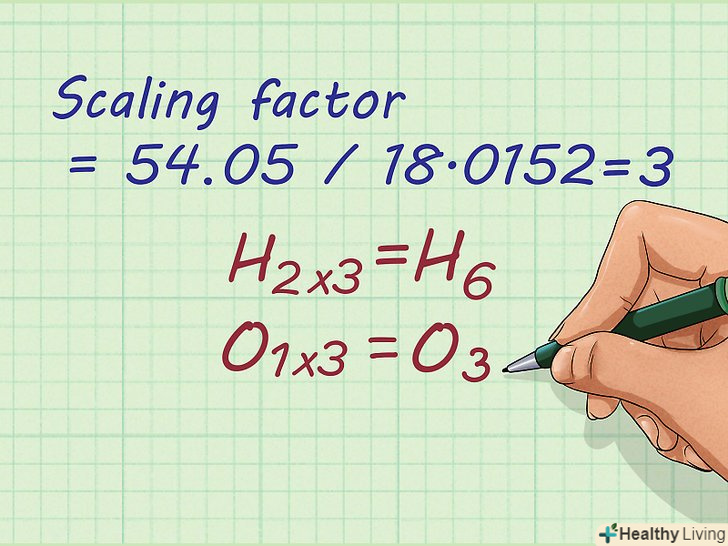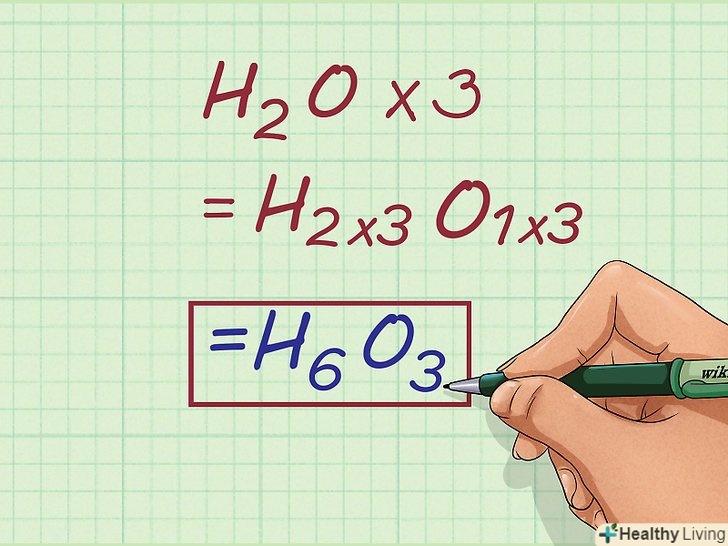Коефіцієнт пропорційності (лінійний коефіцієнт пропорційності) дорівнює відношенню двох відповідних сторін подібних фігур. Подібні фігури - це фігури однакової форми, але різних розмірів. Коефіцієнт пропорційності використовується для вирішення основних геометричних задач. Коефіцієнт пропорційності можна використовувати для обчислення довжин невідомих сторін. З іншого боку, за відповідними сторонами можна обчислити коефіцієнт пропорційності. Такі обчислення пов'язані з операцією множення або зі спрощенням дробів.
Кроки
Метод1З 4:
Обчислення коефіцієнта пропорційності подібних фігур
Метод1З 4:
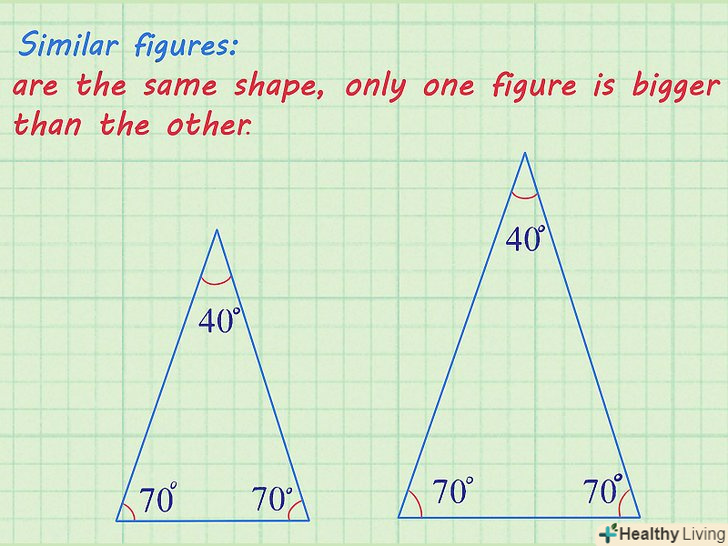
 Переконайтеся, що фігури подібні.у таких фігур всі кути рівні, а сторони співвідносяться в якійсь пропорції. Подібні фігури мають однакову форму, але одна фігура більше іншої.[1]
Переконайтеся, що фігури подібні.у таких фігур всі кути рівні, а сторони співвідносяться в якійсь пропорції. Подібні фігури мають однакову форму, але одна фігура більше іншої.[1]- У завданні повинно бути сказано, що фігури подібні, або що у них рівні кути, або що сторони пропорційні, або що одна фігура пропорційна інший.
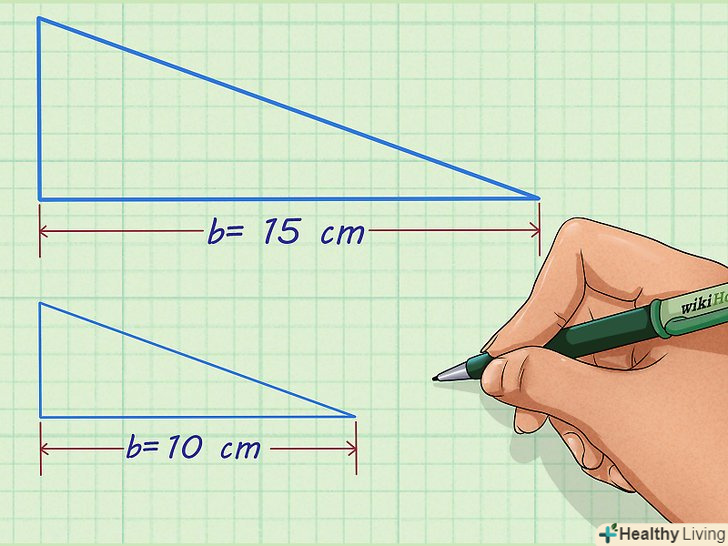
 Знайдіть відповідні сторони обох фігур.можливо, знадобиться повернути або дзеркально відобразити одну з фігур, щоб вирівняти обидві фігури і визначити відповідні сторони. Як правило, в завданнях даються довжини відповідних сторін; в іншому випадку виміряйте їх.[2] якщо не знати значень хоча б пари відповідних сторін, не можна знайти коефіцієнт пропорційності.
Знайдіть відповідні сторони обох фігур.можливо, знадобиться повернути або дзеркально відобразити одну з фігур, щоб вирівняти обидві фігури і визначити відповідні сторони. Як правило, в завданнях даються довжини відповідних сторін; в іншому випадку виміряйте їх.[2] якщо не знати значень хоча б пари відповідних сторін, не можна знайти коефіцієнт пропорційності.- Наприклад, дано трикутник, підстава якого дорівнює 15 см, і подібний трикутник з підставою, рівним 10 см.
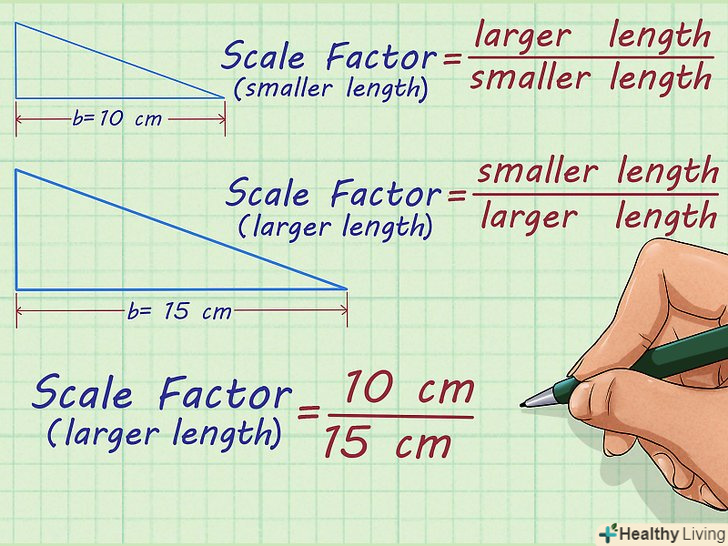
 Запишіть відношення.у кожної пари подібних фігур є два коефіцієнти пропорційності: один використовується при збільшенні розміру, а інший – при зменшенні. Якщо розмір меншої фігури збільшується до розміру більшої фігури, використовуйте відношення: коефіцієнт пропорційності = (сторона більшої фігури)/(сторона меншої фігури). Якщо розмір більшої фігури зменшується до розміру меншої фігури, використовуйте відношення: коефіцієнт пропорційності = (сторона меншої фігури)/(сторона більшої фігури).[3]
Запишіть відношення.у кожної пари подібних фігур є два коефіцієнти пропорційності: один використовується при збільшенні розміру, а інший – при зменшенні. Якщо розмір меншої фігури збільшується до розміру більшої фігури, використовуйте відношення: коефіцієнт пропорційності = (сторона більшої фігури)/(сторона меншої фігури). Якщо розмір більшої фігури зменшується до розміру меншої фігури, використовуйте відношення: коефіцієнт пропорційності = (сторона меншої фігури)/(сторона більшої фігури).[3]- Наприклад, якщо трикутник з основою 15 см зменшується до трикутника з підставою 10 см, використовуйте відношення: коефіцієнт пропорційності = (сторона меншої фігури)/(сторона більшої фігури).
підставивши відповідні значення, Ви отримаєте: коефіцієнт пропорційності =.
- Наприклад, якщо трикутник з основою 15 см зменшується до трикутника з підставою 10 см, використовуйте відношення: коефіцієнт пропорційності = (сторона меншої фігури)/(сторона більшої фігури).
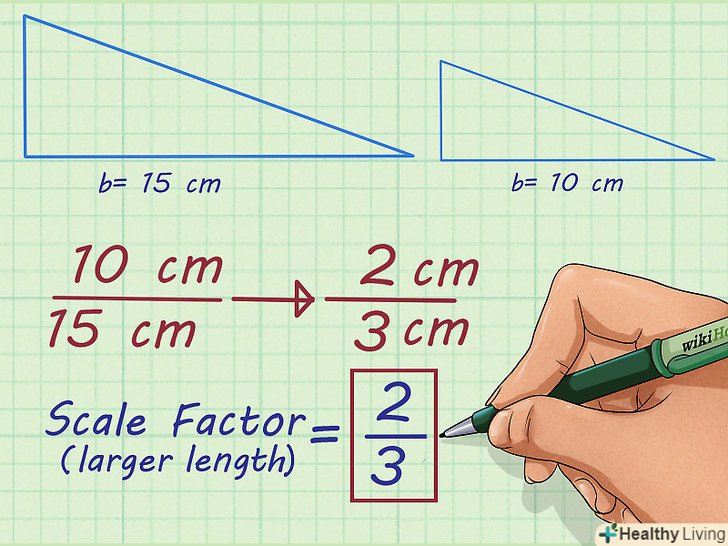
 Спростіть ставлення. спрощене відношення (дріб) є коефіцієнтом пропорційності. При зменшенні розміру коефіцієнт пропорційності являє собою правильну дріб.[4] при збільшенні розміру коефіцієнт пропорційності являє собою ціле число або неправильну дріб, яку можна перетворити в десяткову дріб.
Спростіть ставлення. спрощене відношення (дріб) є коефіцієнтом пропорційності. При зменшенні розміру коефіцієнт пропорційності являє собою правильну дріб.[4] при збільшенні розміру коефіцієнт пропорційності являє собою ціле число або неправильну дріб, яку можна перетворити в десяткову дріб.- Наприклад, відношення
спрощується до
. Таким чином, коефіцієнт пропорційності двох трикутників з підставами 15 см і 10 см дорівнює
.
- Наприклад, відношення
Метод2З 4:
Обчислення сторін за коефіцієнтом пропорційності
Метод2З 4:
 Знайдіть значення сторін фігури.значення сторін однієї з подібних фігур будуть дані; в іншому випадку виміряйте їх. Якщо сторони однієї з подібних фігур невідомі, не можна обчислити сторони другої фігури.
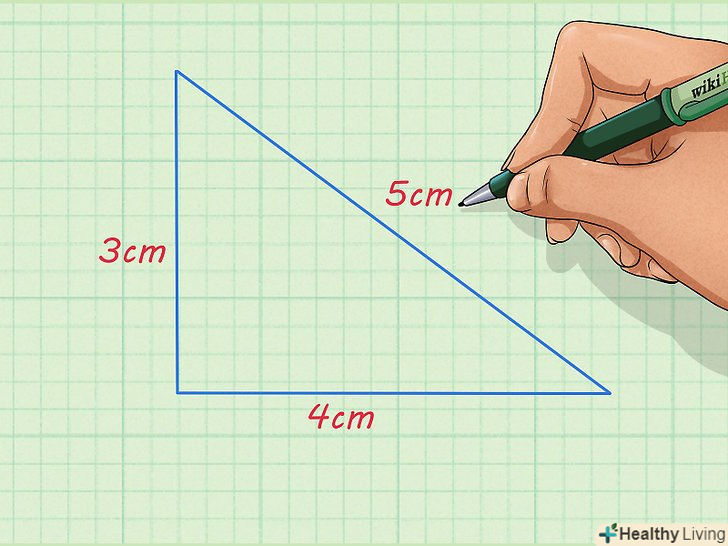
Знайдіть значення сторін фігури.значення сторін однієї з подібних фігур будуть дані; в іншому випадку виміряйте їх. Якщо сторони однієї з подібних фігур невідомі, не можна обчислити сторони другої фігури.- Наприклад, дано прямокутний трикутник, катети якого рівні 4 см і 3 см, а гіпотенуза дорівнює 5 см.
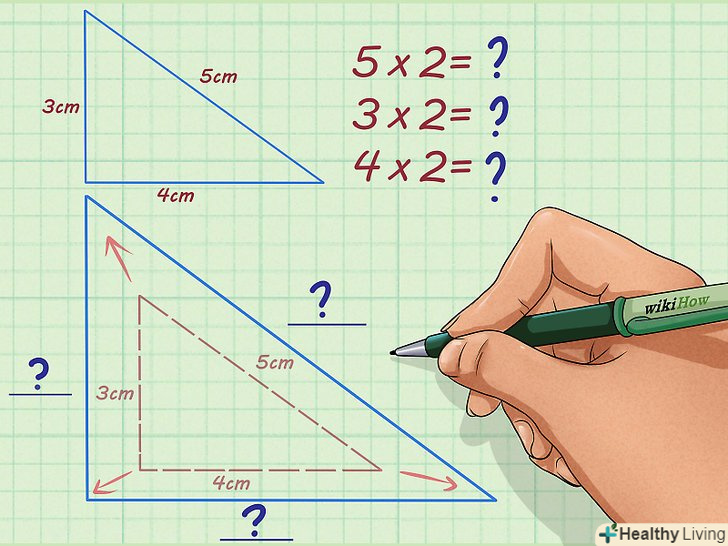
 З'ясуйте, чи буде подібна фігура більше або менше даної. якщо більше, сторони будуть більше, а коефіцієнт пропорційності являє собою ціле число, неправильну або десяткову дріб. Якщо подібна фігура менше даної, сторони будуть менше, а коефіцієнт пропорційності являє собою правильну дріб.
З'ясуйте, чи буде подібна фігура більше або менше даної. якщо більше, сторони будуть більше, а коефіцієнт пропорційності являє собою ціле число, неправильну або десяткову дріб. Якщо подібна фігура менше даної, сторони будуть менше, а коефіцієнт пропорційності являє собою правильну дріб.- Наприклад, якщо коефіцієнт пропорційності дорівнює 2, подібна фігура більше даної.
 Помножте значення однієї сторони на коефіцієнт пропорційності. коефіцієнт пропорційності повинен бути даний. Якщо помножити сторону на коефіцієнт пропорційності, можна знайти значення відповідної сторони подібної фігури.[5]
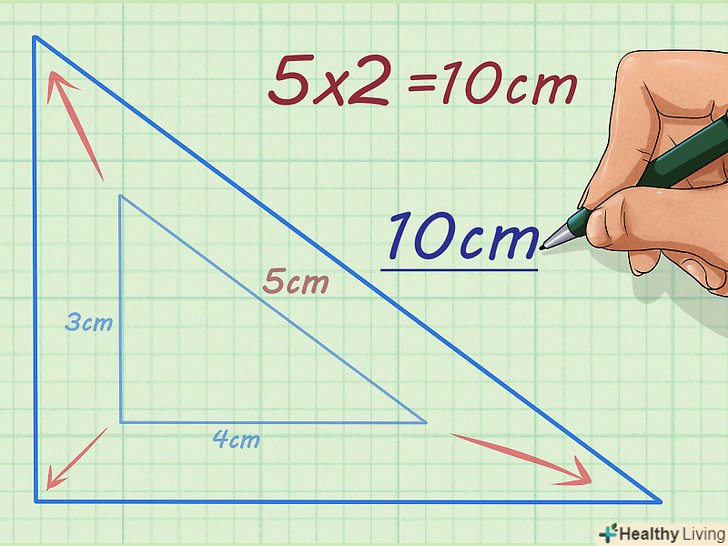
Помножте значення однієї сторони на коефіцієнт пропорційності. коефіцієнт пропорційності повинен бути даний. Якщо помножити сторону на коефіцієнт пропорційності, можна знайти значення відповідної сторони подібної фігури.[5]- Наприклад, якщо гіпотенуза прямокутного трикутника дорівнює 5 см, а коефіцієнт пропорційності дорівнює 2, гіпотенуза подібного трикутника обчислюється так:
. Таким чином, гіпотенуза подібного трикутника дорівнює 10 см.
- Наприклад, якщо гіпотенуза прямокутного трикутника дорівнює 5 см, а коефіцієнт пропорційності дорівнює 2, гіпотенуза подібного трикутника обчислюється так:
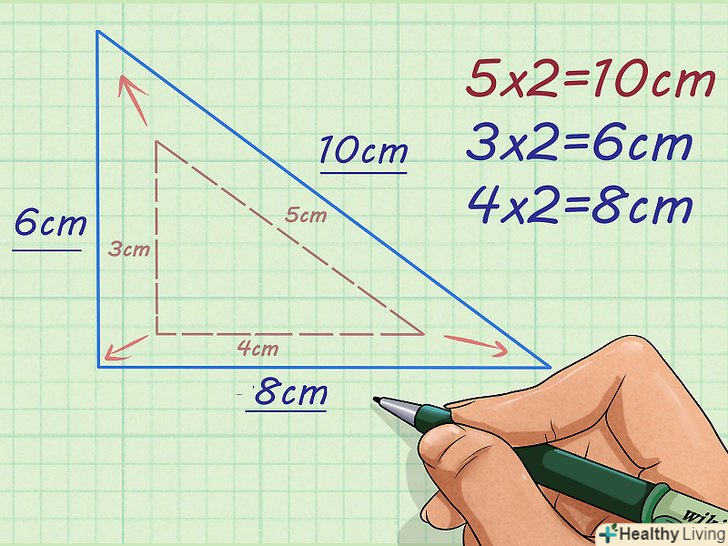
 Знайдіть значення інших сторін подібної фігури.для цього помножте відомі значення сторін на коефіцієнт пропорційності. Ви отримаєте значення відповідних сторін подібної фігури.
Знайдіть значення інших сторін подібної фігури.для цього помножте відомі значення сторін на коефіцієнт пропорційності. Ви отримаєте значення відповідних сторін подібної фігури.- Наприклад, якщо підстава прямокутного трикутника дорівнює 4 см, а коефіцієнт пропорційності дорівнює 2, підстава подібного трикутника обчислюється так:
. Таким чином, підстава подібного трикутника дорівнює 8 см. Якщо катет прямокутного трикутника дорівнює 3 см, а коефіцієнт пропорційності дорівнює 2, катет подібного трикутника обчислюється так:
. Таким чином, катет подібного трикутника дорівнює 6 см.
- Наприклад, якщо підстава прямокутного трикутника дорівнює 4 см, а коефіцієнт пропорційності дорівнює 2, підстава подібного трикутника обчислюється так:
Метод3З 4:
Приклади розв'язання задач
Метод3З 4:
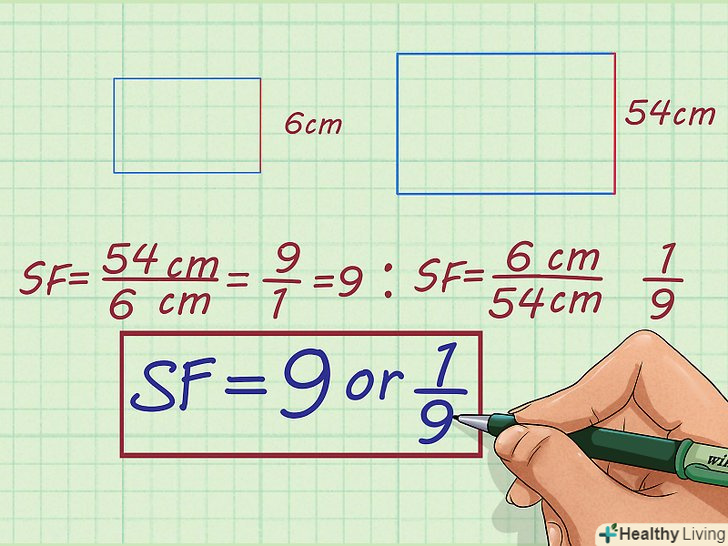
 Завдання 1. знайдіть коефіцієнт пропорційності наступних подібних фігур: прямокутник з шириною 6 см і прямокутник з шириною 54 см.
Завдання 1. знайдіть коефіцієнт пропорційності наступних подібних фігур: прямокутник з шириною 6 см і прямокутник з шириною 54 см.- Запишіть відношення на основі двох значень ширини. При збільшенні розміру відношення запишеться так: коефіцієнт пропорційності =
. При зменшенні розміру відношення запишеться так: коефіцієнт пропорційності =
.
- Спростіть ставлення. Відношення
спрощується до
. Відношення
спрощується до
. Таким чином, коефіцієнт пропорційності двох прямокутників дорівнює
або
.
- Запишіть відношення на основі двох значень ширини. При збільшенні розміру відношення запишеться так: коефіцієнт пропорційності =
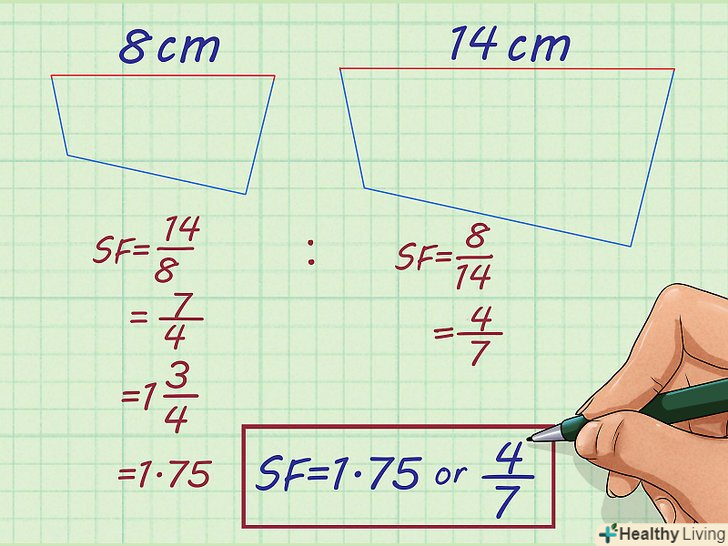
 Задача 2. Сторона неправильного багатокутника дорівнює 14 см.Сторона подібного багатокутника дорівнює 8 см. знайдіть коефіцієнт пропорційності.
Задача 2. Сторона неправильного багатокутника дорівнює 14 см.Сторона подібного багатокутника дорівнює 8 см. знайдіть коефіцієнт пропорційності.- Неправильні фігури подібні, якщо всі їхні сторони пропорційні. Таким чином, коефіцієнт пропорційності можна обчислити за будь-яким відомим значенням.[6]
- Так як відповідні сторони багатокутників відомі, можна записати відношення. При збільшенні розміру відношення запишеться так: коефіцієнт пропорційності =
. При зменшенні розміру відношення запишеться так: коефіцієнт пропорційності =
.
- Спростіть ставлення. Відношення
спрощується до
. Відношення
спрощується до
. Таким чином, коефіцієнт пропорційності двох неправильних багатокутників дорівнює
або
.
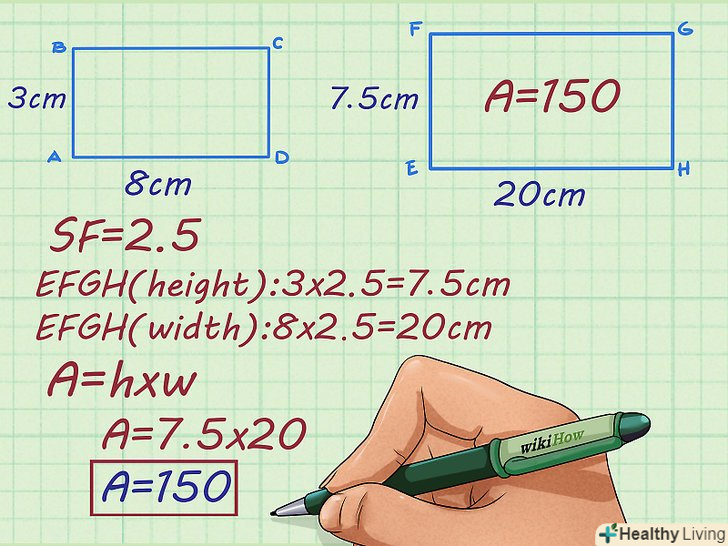
 Завдання 3.сторони прямокутника ABCD рівні 8 см і 3 см.прямокутник EFGH є великим і подібним прямокутником. Знайдіть площу прямокутника EFGH, якщо коефіцієнт пропорційності дорівнює 2,5.
Завдання 3.сторони прямокутника ABCD рівні 8 см і 3 см.прямокутник EFGH є великим і подібним прямокутником. Знайдіть площу прямокутника EFGH, якщо коефіцієнт пропорційності дорівнює 2,5.- Помножте ширину прямокутника ABCD на коефіцієнт пропорційності. Ви знайдете ширину прямокутника EFGH:
.
- Помножте довжину прямокутника ABCD на коефіцієнт пропорційності. Ви знайдете довжину прямокутника EFGH:
.
- Перемножте довжину і ширину прямокутника EFGH, щоб знайти його площа:
. Таким чином, площа прямокутника efgh дорівнює 150 квадратних сантиметрів.
- Помножте ширину прямокутника ABCD на коефіцієнт пропорційності. Ви знайдете ширину прямокутника EFGH:
Метод4З 4:
Обчислення коефіцієнта пропорційності в хімії
Метод4З 4:
 Молярну масу з'єднання розділіть на молярну масу по емпіричній формулі.якщо емпірична формула хімічної сполуки відома і потрібно знайти молекулярну формулу того ж хімічного з'єднання, коефіцієнт пропорційності дорівнює відношенню молярної маси з'єднання до молярної маси за емпіричною формулою.
Молярну масу з'єднання розділіть на молярну масу по емпіричній формулі.якщо емпірична формула хімічної сполуки відома і потрібно знайти молекулярну формулу того ж хімічного з'єднання, коефіцієнт пропорційності дорівнює відношенню молярної маси з'єднання до молярної маси за емпіричною формулою.- Наприклад, знайдіть молярну масу сполуки H2O, молекулярна маса якого дорівнює 54,05 г / моль.
- Молярна маса Н2О дорівнює 18,0152 г/моль.
- Молярну масу з'єднання розділіть на молярну масу за емпіричною формулою:
- Коефіцієнт пропорційності дорівнює 54,05/18,0152 = 3
- Наприклад, знайдіть молярну масу сполуки H2O, молекулярна маса якого дорівнює 54,05 г / моль.
 Емпіричну формулу помножте на коефіцієнт пропорційності.в емпіричній формулі індекси елементів помножте на обчислений коефіцієнт пропорційності. Ви знайдете молекулярну формулу хімічної сполуки, даної в задачі.
Емпіричну формулу помножте на коефіцієнт пропорційності.в емпіричній формулі індекси елементів помножте на обчислений коефіцієнт пропорційності. Ви знайдете молекулярну формулу хімічної сполуки, даної в задачі.- Наприклад, щоб знайти молекулярну формулу даної сполуки, помножте індекси з'єднання Н20 на коефіцієнт пропорційності, рівний 3.
- H2O * 3 = H6O3
- Наприклад, щоб знайти молекулярну формулу даної сполуки, помножте індекси з'єднання Н20 на коефіцієнт пропорційності, рівний 3.
 Напишіть відповідь. знайдені емпірична і молекулярна формули хімічної сполуки, яка дана в задачі.
Напишіть відповідь. знайдені емпірична і молекулярна формули хімічної сполуки, яка дана в задачі.- Наприклад, коефіцієнт пропорційності дорівнює 3. Молекулярна формула сполуки: H6O3.
Джерела
- ↑ Http://www.mathsisfun.com/geometry/similar.html
- ↑ Http://www.virtualnerd.com/pre-algebra/ratios-proportions/similar-figures-indirect-measurement/similar-figures/find-scale-factor-similar-figures
- ↑ Http://www.bbc.co.uk/education/guides/zpwycdm/revision/2
- ↑ Http://www.virtualnerd.com/pre-algebra/ratios-proportions/similar-figures-indirect-measurement/similar-figures/find-scale-factor-similar-figures
- ↑ Http://www.virtualnerd.com/pre-algebra/ratios-proportions/missing-measurements-similar-figures-scale-factor.php
- ↑ Http://www.vias.org/physics/bk1_03_02b.html