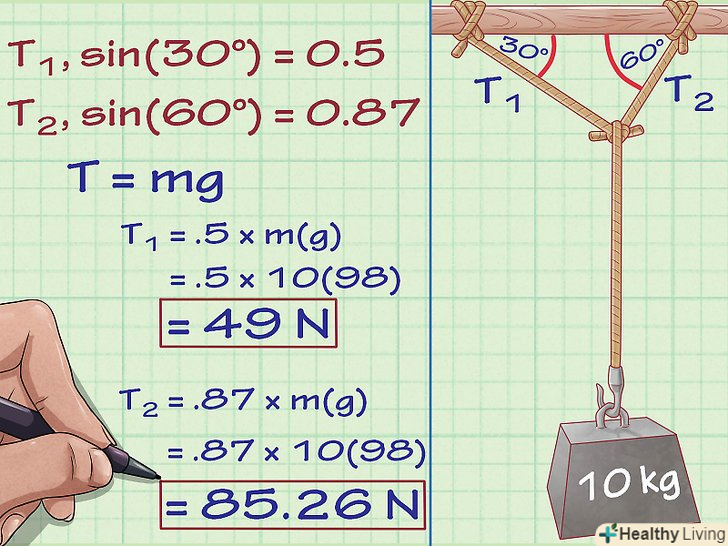1. Головна
    2. Фізика
    3. Як розрахувати силу натягу у фізиці: 8 кроків

Як розрахувати силу натягу у фізиці: 8 кроків

У фізиці, сила натягу-це сила, що діє на мотузку, шнур, кабель або схожий об'єкт або групу об'єктів. Все, що натягнуто, підвішене, підтримується або гойдається на мотузці, шнурі, кабелі і так далі, є об'єктом сили натягу. Подібно всім силам, натяг може прискорювати об'єкти або ставати причиною їх деформації. Уміння розраховувати силу натягу є важливим навиком не тільки для студентів фізичного факультету, а й для інженерів, архітекторів; ті, хто будує стійкі будинки, повинні знати, чи витримає певна мотузка або кабель силу натягу від ваги об'єкта так, щоб вони не просідали і не руйнувалися. Приступайте до читання статті, щоб навчитися розраховувати силу натягу в деяких фізичних системах.

Метод1 З 2:
Визначення сили натягу на одній нитці

  1. Визначте сили на кожному з кінців нитки. Сила натягу даної нитки, мотузки є результатом сил, що натягують мотузку з кожного кінця. Нагадуємо, що сила = маса. Припускаючи, що мотузка натягнута туго, будь-яка зміна прискорення або маси об'єкта, підвішеного на мотузці, призведе до зміни сили натягу в самій мотузці. Не забувайте про постійне прискорення сили тяжіння-навіть якщо система знаходиться в спокої, її складові є об'єктами дії сили тяжіння. Ми можемо припустити, що сила натягу даної мотузки T = (m × g) + (m × a), де «g» — це прискорення сили тяжіння будь-якого з об'єктів, підтримуваних мотузкою, і «а» — це будь-яке інше прискорення, що діє на об'єкти.
    • Для вирішення безлічі фізичних завдань, ми припускаємоідеальну мотузку - іншими словами, наша мотузка тонка, не володіє масою і не може розтягуватися або рватися.
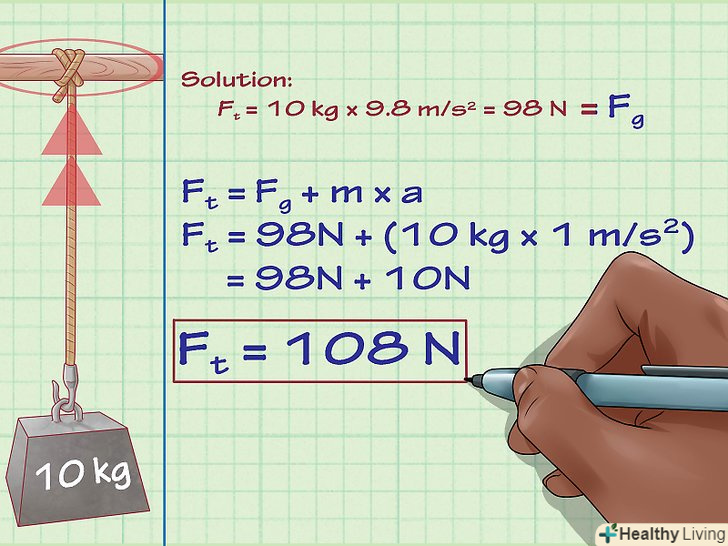
    • Для прикладу, давайте розглянемо систему, в якій вантаж підвішений до дерев'яної балки за допомогою однієї мотузки (дивіться на зображення). Ні сам вантаж, ні мотузка не рухаються-система знаходиться в спокої. Внаслідок цього, нам відомо, щоб вантаж знаходився в рівновазі, сила натягу повинна бути дорівнює силі тяжіння. Іншими словами, Сила натягу (Ft) = Сила тяжіння (Fg) = m × g.
      • Припустимо, що вантаж має масу 10 кг, отже, сила натягу дорівнює 10 кг х 9,8 м/с2 = 98 Ньютонів.
  2. Враховуйте прискорення. Сила тяжіння — не єдина сила, що може впливати на силу натягу мотузки-таку ж дію виробляє будь-яка сила, прикладена до об'єкта на мотузці з прискоренням. Якщо, наприклад, підвішений на мотузці або кабелі об'єкт прискорюється під дією сили, то сила прискорення (маса прискорення) додається до сили натягу, утвореної вагою цього об'єкта.
    • Припустимо, що в нашому прикладі на мотузку підвішений вантаж 10 кг, і замість того, щоб бути прикріпленим до дерев'яної балки, його тягнуть вгору з прискоренням 1 м/с2. В цьому випадку, нам необхідно врахувати прискорення вантажу, також як і прискорення сили тяжіння, наступним чином:
      • Ft = Fg + m × a
      • Ft = 98 + 10 кг × 1 м/с2
      • F t = 108 Ньютонів.
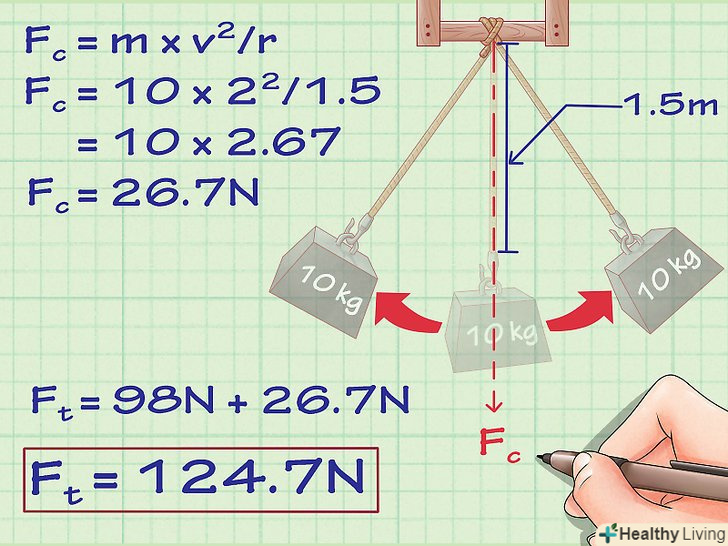
  3. Враховуйте кутове прискорення.об'єкт на мотузці, що обертається навколо точки, яка вважається центром (як маятник), надає натяг на мотузку за допомогою відцентрової сили. Відцентрова сила-додаткова сила натягу, яку викликає мотузка « "штовхаючи" її всередину так, щоб вантаж продовжував рухатися по дузі, а не по прямій. Чим швидше рухається об'єкт, тим більше відцентрова сила. Відцентрова сила (Fc) дорівнює MX v2/r де «m»– це маса, «v» — це швидкість, і «r» — радіус кола, по якій рухається вантаж.
    • Так як напрямок і значення відцентрової сили змінюються в залежності від того, як об'єкт рухається і змінює свою швидкість, то повне натяг мотузки завжди паралельно мотузці в центральній точці. Запам'ятайте, що сила тяжіння постійно діє на об'єкт і тягне його вниз. Так що, якщо об'єкт розгойдується вертикально, повне натягнайсильніше в нижній точці дуги (для маятника це називається точкою рівноваги), коли об'єкт досягає максимальної швидкості, і найслабше у верхній точці дуги, коли об'єкт сповільнюється.
    • Давайте припустимо, що в нашому прикладі об'єкт більше не прискорюється вгору, а розгойдується як маятник. Нехай наша мотузка буде довжиною 1,5 м, а наш вантаж рухається зі швидкістю 2 м/с, при проходженні через нижню точку розмаху. Якщо нам потрібно розрахувати силу натягу в нижній точці дуги, коли вона найбільша, то спочатку треба з'ясувати Рівне чи тиск сили тяжіння відчуває вантаж в цій точці, як і при стані спокою — 98 Ньютонів. Щоб знайти додаткову відцентрову силу, нам необхідно вирішити наступне:
      • Fc = m × v2/r
      • Fc = 10 × 22/1.5
      • Fc =10 × 2,67 = 26,7 Ньютонів.
      • Таким чином, повний натяг буде 98 + 26,7 =124,7 Ньютона.
  4. Врахуйте, що сила натягу завдяки силі тяжіння змінюється в міру проходження вантажу по дузі.як було зазначено вище, напрямок і величина відцентрової сили змінюються в міру того, як гойдається об'єкт. У будь-якому випадку, хоча сила тяжіння і залишається постійною,результуюча сила натягу в результаті тяжкості теж змінюється. Коли гойдається об'єкт знаходиться не в нижній точці дуги (точці рівноваги), сила тяжіння тягне його вниз, але сила натягу тягне його вгору під кутом. З цієї причини сила натягу повинна протидіяти частині сили тяжіння, а не всій її повноті.
    • Поділ сили гравітації на два вектори зможе допомогти вам візуально зобразити цей стан. У будь-якій точці дуги вертикально розгойдується об'єкта, мотузка становить кут «θ» з лінією, що проходить через точку рівноваги і центр обертання. Як тільки маятник починає розгойдуватися, сила гравітації(MX g) розбивається на 2 вектора — mgsin(θ), діючи по дотичній до дуги в напрямку точки рівноваги і mgcos (θ), діючи паралельно силі натягу, але в протилежному напрямку. Натяг може тільки протистояти mgcos — θ) — силі, спрямованої проти неї-не всій силі тяжіння (виключаючи точку рівноваги, де всі сили однакові).
    • Давайте припустимо, що, коли маятник відхиляється на кут 15 градусів від вертикалі, він рухається зі швидкістю 1,5 м / с. ми знайдемо силу натягу наступними діями:
      • Відношення сили натягу до сили тяжіння (Tg) = 98cos(15) = 98(0,96) = 94,08 Ньютона
      • Відцентрова сила (Fc) = 10 × 1,52/1,5 = 10 × 1,5 = 15 Ньютонів
      • Повне натяг = Tg + F c = 94,08 + 15 = 109,08 Ньютонів.
  5. Розрахуйте тертя.будь-який об'єкт, який тягнеться мотузкою і відчуває силу «гальмування» від тертя іншого об'єкта (або рідини), передає цей вплив натягу в мотузці. Сила тертя між двома об'єктами розраховується також, як і в будь — якій іншій ситуації — за наступним рівнянням: Сила тертя (зазвичай пишеться як Fr) = (mu)N, де mu — це коефіцієнт сили тертя між об'єктами і N-звичайна сила взаємодії між об'єктами, або та сила, з якою вони тиснуть один на одного. Відзначимо, що тертя спокою — це тертя, яке виникає в результаті спроби привести об'єкт, що знаходиться в спокої, в рух — відрізняється від тертя руху — тертя, що виникає в результаті спроби змусити рухомий об'єкт продовжувати рух.
    • Давайте припустимо, що наш вантаж в 10 кг більше не розгойдується, тепер його буксирують по горизонтальній площині за допомогою мотузки. Припустимо, що коефіцієнт тертя руху Землі дорівнює 0,5 і наш вантаж рухається з постійною швидкістю, але нам потрібно надати йому прискорення 1м/с2. Ця проблема представляє дві важливі зміни-перше, нам більше не потрібно розраховувати силу натягу по відношенню до сили тяжіння, так як наша мотузка не утримує вантаж на вазі. Друге, нам доведеться розрахувати натяг, обумовлене тертям, також як і викликане прискоренням маси вантажу. Нам потрібно вирішити наступне:
      • Звичайна сила (N) = 10 кг &#amp; x 9,8 (прискорення сили тяжіння) = 98 N
      • Сила тертя руху (Fr) = 0,5 x 98 N = 49 Ньютонів
      • Сила прискорення (Fa) = 10 kg x 1 м / с2 = 10 Ньютонів
      • Загальний натяг = F r + F a = 49 + 10 = 59 Ньютонів.

Метод2 З 2:
Розрахунок сили натягу на декількох нитках

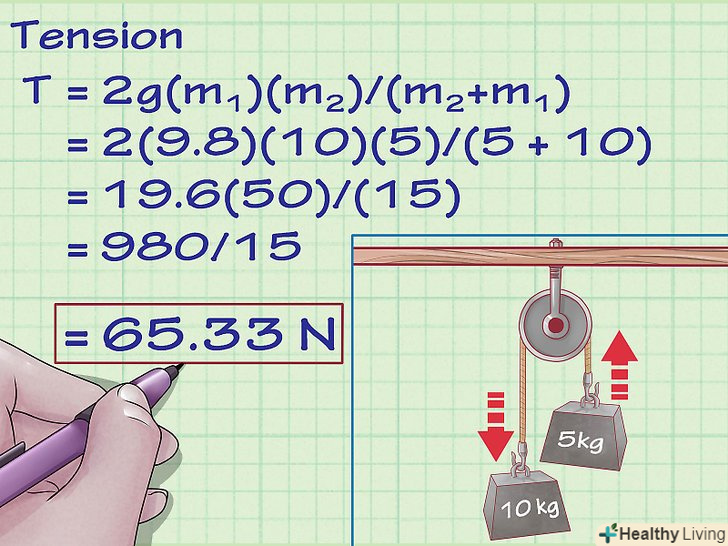
  1. Підніміть вертикальні паралельні вантажі за допомогою блоку. Блоки-це прості механізми, що складаються з підвісного диска, що дозволяє змінювати напрямок сили натягу мотузки. У простій конфігурації блоку, мотузка або кабель йде від підвішеного вантажу вгору до блоку, потім вниз до іншого вантажу, створюючи тим самим дві ділянки мотузки або кабелю. У будь-якому випадку натяг в кожній з ділянок буде однаковим, навіть якщо обидва кінці будуть натягуватися силами різних величин. Для системи двох мас, підвішених вертикально в блоці, сила натягу дорівнює 2G(m1) (m2)/(m2+m1), де «g» — прискорення сили тяжіння, «m1» — маса першого об'єкта, «m2»– маса другого об'єкта.
    • Відзначимо наступне, фізичні завдання припускають, щоблоки ідеальні - не мають маси, тертя, вони не ламаються, не деформуються і не відокремлюються від мотузки, яка їх підтримує.
    • Давайте припустимо, що у нас є два вертикально підвішених на паралельних кінцях мотузки вантажу. У одного вантажу Маса 10 кг, а у другого — 5 кг. у цьому випадку, нам необхідно розрахувати наступне:
      • T = 2g(m1)(m2)/(m2+m1)
      • T = 2(9,8)(10)(5)/(5 + 10)
      • T = 19,6(50)/(15)
      • T = 980/15
      • T =65,33 Ньютонів.
    • Відзначимо, що, так як один вантаж важче, всі інші елементи рівні, ця система почне прискорюватися, отже, вантаж 10 кг буде рухатися вниз, змушуючи другий вантаж йти вгору.
  2. Підвісьте вантажі, використовуючи блоки з не паралельними вертикальними нитками.блоки часто використовуються для того, щоб направляти силу натягу в напрямку, відмінному від напрямку вниз або вгору. Якщо, наприклад, вантаж підвішений вертикально до одного кінця мотузки, а інший кінець тримає вантаж в діагональній площині, то непаралельна система блоків приймає форму трикутника з кутами в точках з перших вантажем, другим і самим блоком. В цьому випадку натяг в мотузці залежить як від сили тяжіння, так і від складової сили натягу, яка паралельна до діагональної частини мотузки.
    • Давайте припустимо, що у нас є система з вантажем в 10 кг (m1 ), підвішеним вертикально, з'єднаний з вантажем в 5 кг (m2), розташованим на похилій площині в 60 градусів (вважається, що цей ухил не дає тертя). Щоб знайти натяг в мотузці, найлегшим шляхом буде спочатку скласти рівняння для сил, що прискорюють вантажі. Далі діємо так:
      • Підвішений вантаж важче, тут немає тертя, так що ми знаємо, що він прискорюється вниз. Натяг в мотузці тягне вгору, так що він прискорюється по відношенню до рівнодіючої силі F = m1(g) - T, або 10( 9,8) - T = 98-T.
      • Ми знаємо, що вантаж на похилій площині прискорюється вгору. Так як вона не має тертя, ми знаємо, що натяг тягне вантаж вгору по площині, а вниз його тягнеТільки свою власну вагу. Складова сили, що тягне вниз по похилій, обчислюється як mgsin(θ), так що в нашому випадку ми можемо зробити висновок, що він прискорюється по відношенню до рівнодіючої силі F = T - m2(g)sin(60) = T - 5(9,8) (0,87) = T — 42,14.
      • Якщо ми прирівняємо ці два рівняння, то вийде 98 - T = T - 42,14. Знаходимо Т і отримуємо 2t = 140,14, або T = 70,07 Ньютонів.
  3. Використовуйте кілька ниток, щоб підвісити об'єкт.на закінчення, давайте уявимо, що об'єкт підвішений на «Y-образної» системі мотузок — дві мотузки закріплені на стелі і зустрічаються в центральній точці, з якої йде третя мотузка з вантажем. Сила натягу третьої мотузки очевидна-просте натяг в результаті дії сили тяжіння або m(g). Натяги на двох інших мотузках розрізняються і повинні складати в сумі силу, рівну силі тяжіння вгору у вертикальному положенні і дорівнюють нулю в обох горизонтальних напрямках, якщо припустити, що система знаходиться в стані спокою. Натяг в мотузці залежить від маси підвішених вантажів і від кута, на який відхиляється від стелі кожна з мотузок.
    • Давайте припустимо, що в нашій Y-образній системі нижній вантаж має масу 10 кг і підвішений на двох мотузках, кут однієї з яких становить зі стелею 30 градусів, а кут другий — 60 градусів. Якщо нам потрібно знайти натяг в кожній з мотузок, нам знадобиться розрахувати горизонтальну і вертикальну складові натягу. Щоб знайти T1 (натяг в тій мотузці, нахил якої 30 градусів) і T2 (натяг в тій мотузці, нахил якої 60 градусів), потрібно вирішити:
      • Відповідно до законів тригонометрії, відношення між T = M (g) і T1 і T2 дорівнює косинусу кута між кожною з мотузок і стелею. Для t1, cos(30) = 0,87, як для T2, cos (60) = 0,5
      • Помножте натяг у нижній мотузці (T=mg) на косинус кожного кута, щоб знайти T1 і T2.
      • T1 = 0,87 × m(g) = 0,87 × 10(9,8) = 85,26 Ньютонів.
      • T2 =0,5 x M(g) = 0,5 × 10(9,8) = 49 Ньютонів.

Джерела

  1. Http://dev.physicslab.org/Document.aspx?doctype=3&#amp;filename=OscillatoryMotion_VerticalCircles.xml
  2. Http://www.idahoforests.org/img/pdf/lessons/calibration.pdf

Ще почитати: