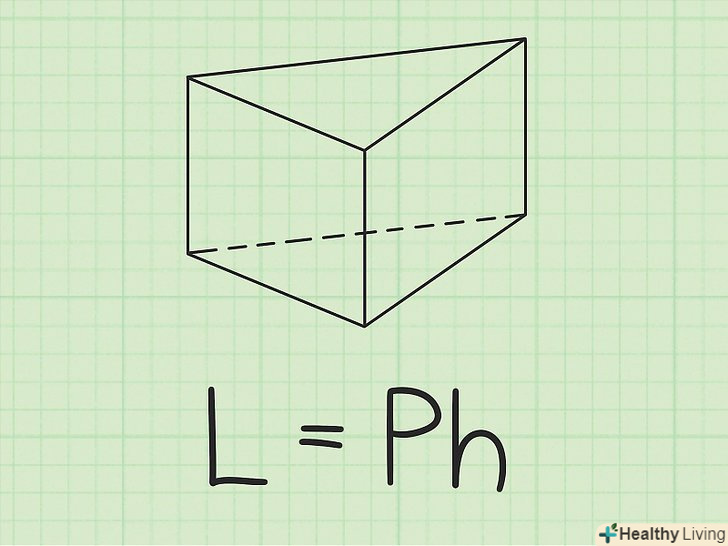
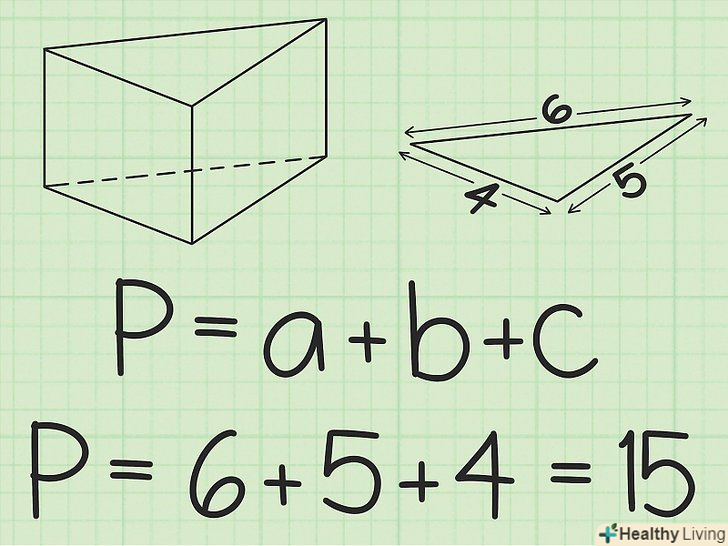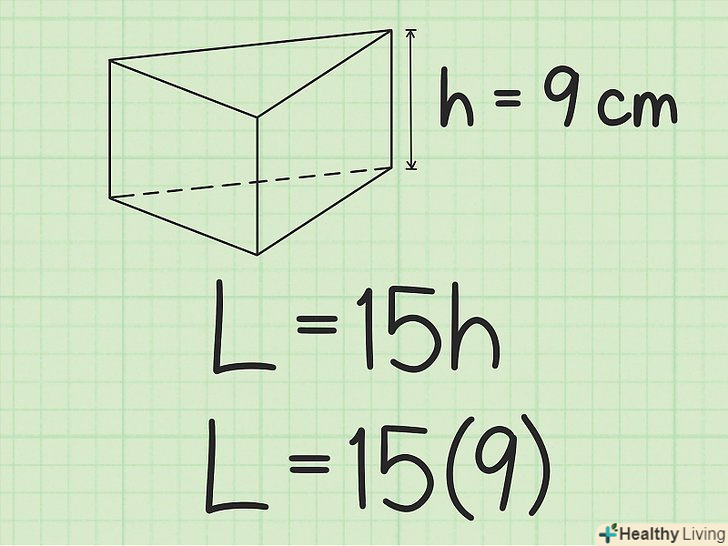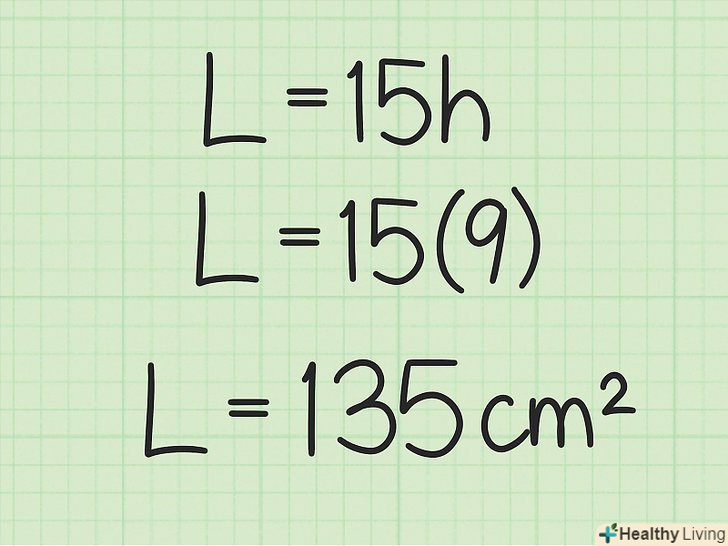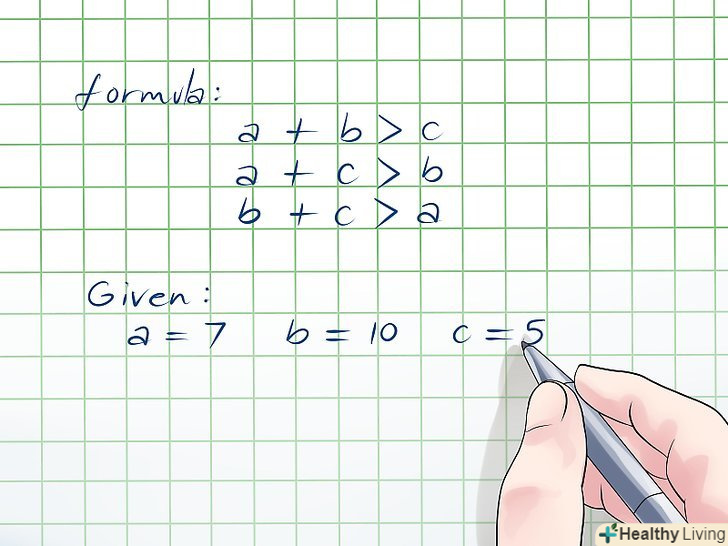Призма являє собою об'ємну (тривимірну) фігуру з двома паралельними (і рівними) гранями.[1] дві паралельні грані є трикутниками і називаються підставами. Також в трикутній призмі є три бічні грані. Щоб знайти площу поверхні трикутної призми, спочатку потрібно обчислити площу бічної поверхні, потім обчислити загальну площу підстав і, нарешті, скласти ці площі. Площа поверхні призми знаходиться за формулою: , де
– площа поверхні,
– площа бічної поверхні,
– площа однієї підстави.
Кроки
Частина1З 3:
Обчислення площі бічної поверхні
Частина1З 3:

 Обчисліть периметр однієї основи.основа являє собою трикутник, тому має три сторони. Периметра трикутника обчислюється за формулою:
Обчисліть периметр однієї основи.основа являє собою трикутник, тому має три сторони. Периметра трикутника обчислюється за формулою:, де
,
,
– сторони трикутника.[4] Не має значення, яку підставу розглядати, так як обидва підстави рівні.[5]
- Наприклад, сторони підстави рівні 6 см, 5 см і 4 см; щоб обчислити периметр, потрібно скласти три сторони:
. Таким чином, периметр однієї основи дорівнює 15 см.
- Наприклад, сторони підстави рівні 6 см, 5 см і 4 см; щоб обчислити периметр, потрібно скласти три сторони:
 Підставте периметр підстави в формулу для обчислення площі бічної поверхні призми. значення периметра підставляється замість
Підставте периметр підстави в формулу для обчислення площі бічної поверхні призми. значення периметра підставляється замість.
- Наприклад,
.
- Наприклад,
 Підставте висоту призми в формулу для обчислення площі бічної поверхні призми.Висота призми дорівнює будь-якій стороні бічної грані, яка не належить основи. Як правило (але не завжди), такою стороною є більш довга сторона бічної грані.
Підставте висоту призми в формулу для обчислення площі бічної поверхні призми.Висота призми дорівнює будь-якій стороні бічної грані, яка не належить основи. Як правило (але не завжди), такою стороною є більш довга сторона бічної грані.- Наприклад, якщо висота призми дорівнює 9 см, формула запишеться так:
.
- Наприклад, якщо висота призми дорівнює 9 см, формула запишеться так:
 Перемножте периметр однієї основи і висоту призми.вийде площа бічної поверхні призми (в квадратних одиницях). Це перше значення, необхідне для обчислення площі поверхні призми (другим значенням є площа основи).
Перемножте периметр однієї основи і висоту призми.вийде площа бічної поверхні призми (в квадратних одиницях). Це перше значення, необхідне для обчислення площі поверхні призми (другим значенням є площа основи).- Наприклад,
. Таким чином, площа бічної поверхні призми дорівнює 135 см2.
- Наприклад,
Частина2З 3:
Обчислення площі підстави
Частина2З 3:
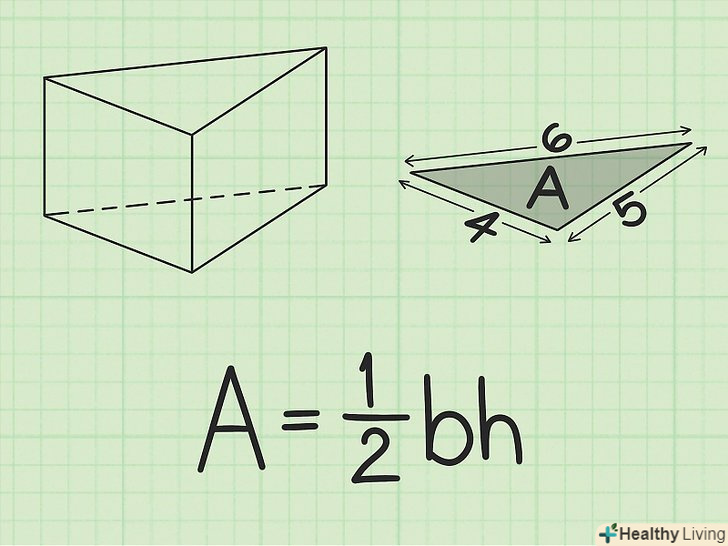
 Запишіть формулу для обчислення площі трикутника.оскільки кожна основа трикутної призми є трикутником, для обчислення площі основи скористайтеся наступною формулою:
Запишіть формулу для обчислення площі трикутника.оскільки кожна основа трикутної призми є трикутником, для обчислення площі основи скористайтеся наступною формулою:, де
– площа трикутника,
– підстава трикутника,
– висота, проведена до основи трикутника.[6]
- Це найпоширеніша формула для обчислення площі трикутника. Якщо висота трикутника не дана,обчисліть площу по трьох сторонах трикутника.
- Потрібно знайти площу тільки однієї основи, так як обидва підстави призми рівні і, отже, мають однакову площу.[7]
 Підставте підставу трикутника в формулу для обчислення площі трикутника.не переплутайте підставу з іншою стороною трикутника. Підстава - це сторона, до якої проведена висота (тобто сторона, перпендикулярна висоті).
Підставте підставу трикутника в формулу для обчислення площі трикутника.не переплутайте підставу з іншою стороною трикутника. Підстава - це сторона, до якої проведена висота (тобто сторона, перпендикулярна висоті).- Наприклад, якщо основа трикутника дорівнює 6 см, формула запишеться так:
.
- Наприклад, якщо основа трикутника дорівнює 6 см, формула запишеться так:
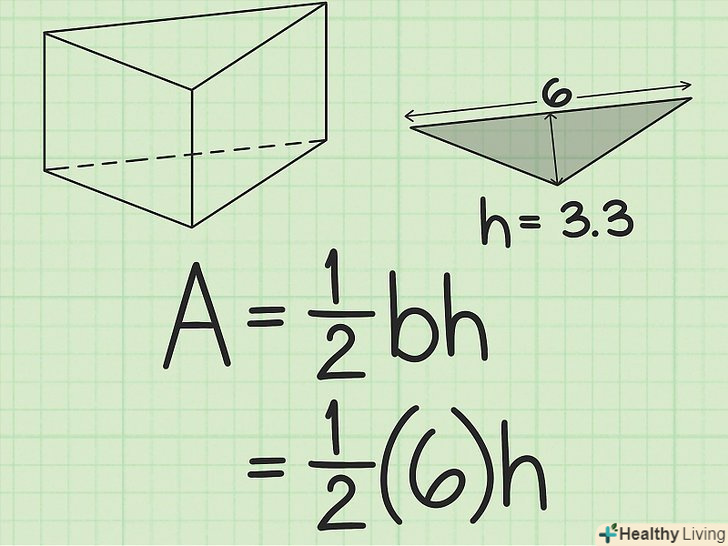
 Підставте висоту трикутника в формулу для обчислення площі трикутника.помножте підставу на висоту, а результат розділіть на 2. Вийде площа підстави (в квадратних одиницях). Це друге значення, необхідне для обчислення площі поверхні призми.
Підставте висоту трикутника в формулу для обчислення площі трикутника.помножте підставу на висоту, а результат розділіть на 2. Вийде площа підстави (в квадратних одиницях). Це друге значення, необхідне для обчислення площі поверхні призми.- Наприклад, якщо висота дорівнює 3,3 см, то розрахунки будуть виглядати наступним чином:
Таким чином, площа основи дорівнює 9,9 см2.
- Наприклад, якщо висота дорівнює 3,3 см, то розрахунки будуть виглядати наступним чином:
Частина3З 3:
Обчислення площі поверхні
Частина3З 3:
 Запишіть формулу для обчислення площі поверхні призми. Формула:
Запишіть формулу для обчислення площі поверхні призми. Формула:, де
– площа поверхні,
– площа бічної поверхні,
– площа однієї основи.[8]
 Підставте площу бічної поверхні в формулу. це загальна площа трьох бічних граней (тобто площі підстав не враховуються), яка була обчислена в першому розділі. Площа бічної поверхні підставляється замість
Підставте площу бічної поверхні в формулу. це загальна площа трьох бічних граней (тобто площі підстав не враховуються), яка була обчислена в першому розділі. Площа бічної поверхні підставляється замість.
- У нашому прикладі площа бічної поверхні дорівнює 135 см2, тому формула запишеться так:
.
- У нашому прикладі площа бічної поверхні дорівнює 135 см2, тому формула запишеться так:
 Підставте площу підстави в формулу.підставляйте площу тільки однієї підстави, а не суму площ двох підстав. Площа підстави підставляється замість
Підставте площу підстави в формулу.підставляйте площу тільки однієї підстави, а не суму площ двох підстав. Площа підстави підставляється замість.
- У нашому прикладі площа основи дорівнює 9,9 см2, тому формула запишеться так:
.
- У нашому прикладі площа основи дорівнює 9,9 см2, тому формула запишеться так:
 Проведіть обчислення.помножте площу підстави на 2, а потім до результату додайте площу бічної поверхні. Вийде площа поверхні трикутної призми (в квадратних одиницях).
Проведіть обчислення.помножте площу підстави на 2, а потім до результату додайте площу бічної поверхні. Вийде площа поверхні трикутної призми (в квадратних одиницях).- Наприклад:
Таким чином, площа поверхні трикутної призми, сторони основи якої рівні 6 см, 5 см і 4 см, а висота дорівнює 9 см, дорівнює 154,8 см2.
- Наприклад:
Джерела
- ↑ Http://www.mathopenref.com/prism.html
- ↑ Http://www.virtualnerd.com/geometry/surface-area-volume-solid/prisms-cylinders-area/triangular-prism-lateral-surface-areas
- ↑ Http://mathcentral.uregina.ca/qq/database/qq.09.06/s/crystal1.html
- ↑ Http://www.mathopenref.com/triangleperimeter.html
- ↑ Http://www.regentsprep.org/regents/math/geometry/gg2/PrismPage.htm
- ↑ Http://www.mathwarehouse.com/geometry/triangles/area/index.php
- ↑ Http://www.regentsprep.org/regents/math/geometry/gg2/PrismPage.htm
- ↑ Https://www.andrews.edu/~calkins/math/webtexts/geom10.htm