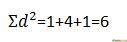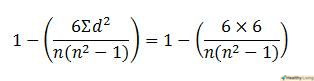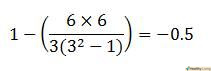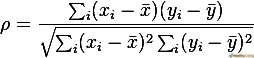Коефіцієнт кореляції рангу Спірмена дозволяє визначити, чи існує між двома змінними залежність, що виражається монотонною функцією (тобто при зростанні однієї змінної збільшується і друга, і навпаки). Наведені в статті прості кроки дозволять вам проводити розрахунки вручну, а також обчислювати коефіцієнт кореляції за допомогою програм Excel і R.
Кроки
Метод1З 3:
Обчислення вручну
Метод1З 3:
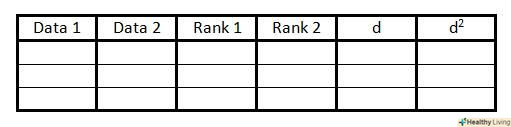
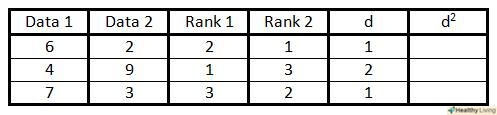
 Складіть таблицю даних.таким чином ви впорядкуєте інформацію, необхідну для розрахунку коефіцієнта кореляції рангу Спірмена. При цьому вам знадобиться:
Складіть таблицю даних.таким чином ви впорядкуєте інформацію, необхідну для розрахунку коефіцієнта кореляції рангу Спірмена. При цьому вам знадобиться:- 6 колонок, названих так, як показано вище на малюнку.
- Кількість рядків, що відповідає числу пар змінних.
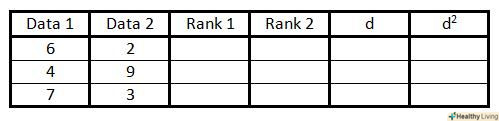
 Заповніть перші дві колонки парами змінних.
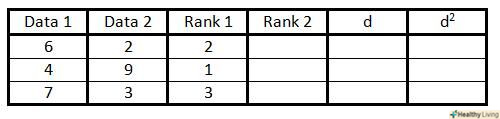
Заповніть перші дві колонки парами змінних. У третій колонці запишіть номери (ранги) пар змінних від 1 доn (загальне число пар). Присвойте номер 1 парі з найменшим значенням в першій колонці, 2 -- наступного за ним значенням , і так по зростанню величин змінної з першої колонки.
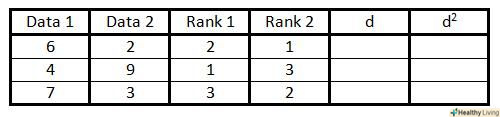
У третій колонці запишіть номери (ранги) пар змінних від 1 доn (загальне число пар). Присвойте номер 1 парі з найменшим значенням в першій колонці, 2 -- наступного за ним значенням , і так по зростанню величин змінної з першої колонки. У четвертій колонці зробіть те ж, що і в третій, але на цей раз пронумеруйте пари змінних по другій колонці таблиці.
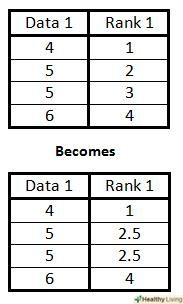
У четвертій колонці зробіть те ж, що і в третій, але на цей раз пронумеруйте пари змінних по другій колонці таблиці.- Якщо два (або більше) значення змінної в одній колонці однакові, розташуйте їх один за іншим і знайдіть середнє значення їх номерів, потім пронумеруйте їх цим середнім значенням.

у наведеному праворуч прикладі два значення змінної збігаються і дорівнюють 5; у разі нормальної нумерації ці дані отримали б ранги 2 і 3. Оскільки значення однакові, знаходимо середню величину їх рангів. Середнє 2 і 3 дорівнює 2,5, тому обом величинам присвоюємо ранг 2,5.
 У колонці "d" обчисліть різницю між двома рангами з попередніх двох колонок.наприклад, якщо ранг в третій колонці дорівнює 1, а в четвертій – 3, то різниця між ними складе 2. Знак не має значення, оскільки на наступному кроці ці числа будуть зведені в квадрат.
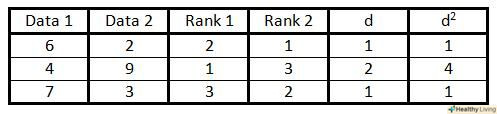
У колонці "d" обчисліть різницю між двома рангами з попередніх двох колонок.наприклад, якщо ранг в третій колонці дорівнює 1, а в четвертій – 3, то різниця між ними складе 2. Знак не має значення, оскільки на наступному кроці ці числа будуть зведені в квадрат. Зведіть кожне значення з колонки " d "в квадрат і запишіть отримані величини в колонку"d2".
Зведіть кожне значення з колонки " d "в квадрат і запишіть отримані величини в колонку"d2".- Підсумуйте всі значення з колонки "d2". ви визначите суму Σd2 .

- Скористайтеся однією з наступних формул:
- Якщо на попередніх кроках не зустрічалося однакових величин, просто підставте отриману суму спрощену формулу для розрахунку коефіцієнта рангової кореляції Спірмена:

і замість " n " підставте число пар даних, внесених Вами раніше в таблицю.
- Якщо на попередніх кроках траплялися однакові значення, скористайтеся стандартною формулою для обчислення коефіцієнта рангової кореляції Спірмена:

- Якщо на попередніх кроках не зустрічалося однакових величин, просто підставте отриману суму спрощену формулу для розрахунку коефіцієнта рангової кореляції Спірмена:
- Проаналізуйте результат. отримане значення знаходиться між -1 і 1.
- Якщо воно близьке до -1, кореляція негативна.
- Якщо близько до 0, кореляція відсутня.
- Якщо близько до 1, спостерігається позитивна кореляція.
- Не забудьте поділити на суму змінних і взяти корінь. Після цього поділіть на Σd2.

Метод2 З 3:
Обчислення в Excel
Метод2 З 3:
- Створіть нові колонки з рангами, відповідними колонкам даних.наприклад, якщо дані внесені в Колонку A2:A11,використовуйте функцію "=RANK(A2, A$2:A$11)" і занесіть результати для всіх рядків в нову колонку.
- Знайдіть ранги для однакових величин, як описано в кроках 3 і 4 методу 1.
- У новій комірці визначте кореляцію між двома колонками рангів за допомогою функції " =CORREL (C2:C11,D2: D11)".в даному випадку C і D-це колонки, що містять ранги. Таким чином, в даній комірці Ви отримаєте коефіцієнт рангової кореляції Спірмена.
Метод3 З 3:
Обчислення в R
Метод3 З 3:
- Якщо у вас ще немає програми R для обробки статистичних даних, придбайте її (див. http://www.r-project.org).
- Збережіть дані у форматі CSV, розташувавши їх у двох колонках, кореляцію між якими ви збираєтеся досліджувати.зберегти файл в даному форматі легко за допомогою опції"Зберегти як".
- Відкрийте редактор R. якщо ви ще не ввійшли в програму R, просто запустіть її. Для цього достатньо натиснути іконку R на робочому столі.
- Наберіть команди:
- D &#lt;- read.csv("NAME_OF_YOUR_CSV.csv") і натисніть клавішу введення
- Cor(rank(d[,1]),rank(d[,2]))
Поради
- Як правило, набір даних повинен складатися не менше ніж з 5 пар для того, щоб можна було достовірно встановити будь-яку кореляцію (3 пари було використано в прикладі вище для простоти).
Попередження
- Коефіцієнт рангової кореляції Спірмена дозволяє встановити лише те, чи ростуть обидві змінні або зменшуються одночасно. Якщо розкид даних занадто великий, цей коефіцієнт не дасть точного значення кореляції.
- Наведена функція дасть вірний результат при відсутності однакових значень в масиві даних. Якщо такі значення існують, як в розглянутому нами прикладі, необхідно використовувати наступне визначення: коефіцієнт кореляції, заснований на рангах.