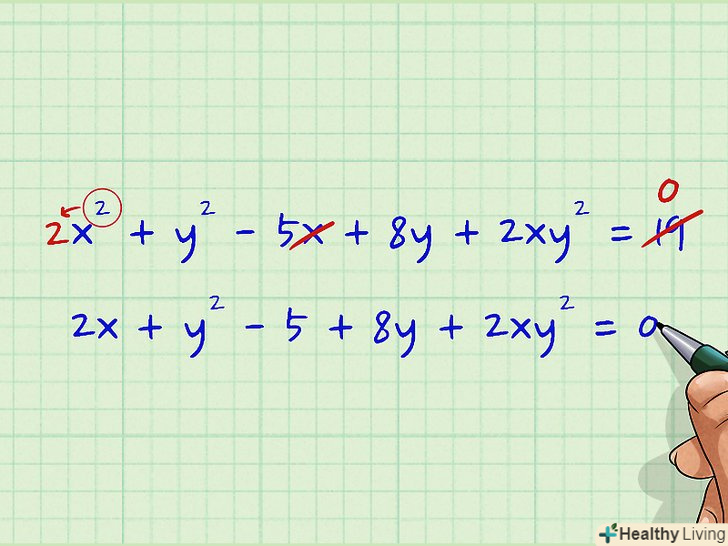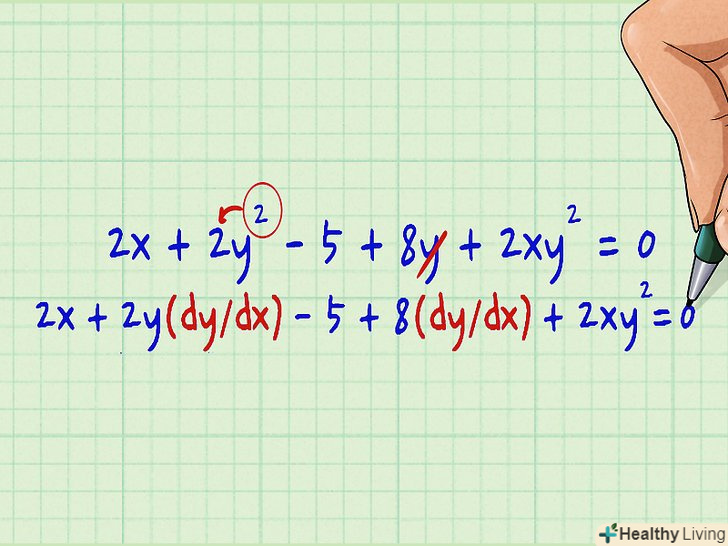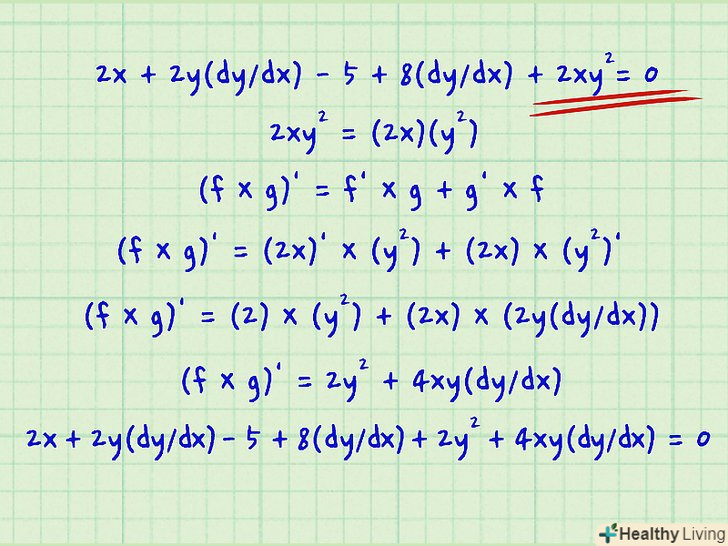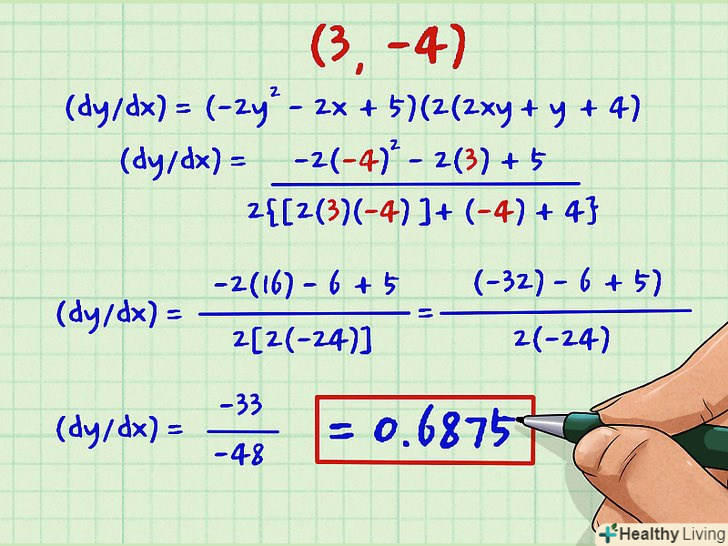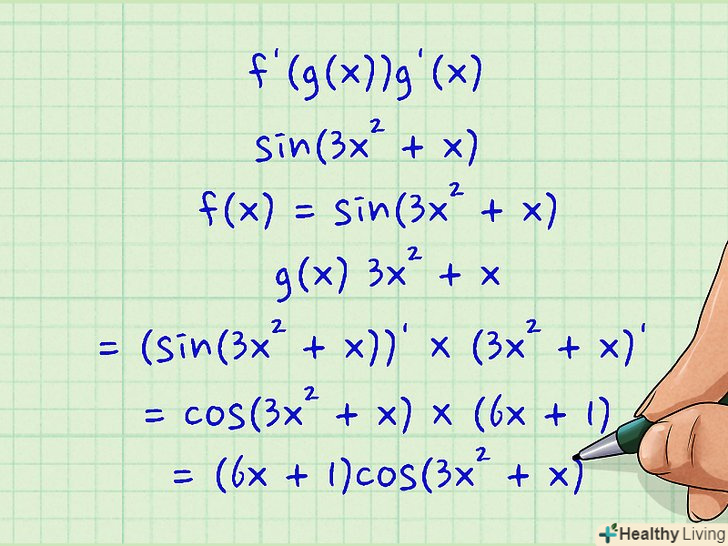1. Головна
    2. Математика
    3. Як продифференцировать неявну функцію: 7 кроків

Як продифференцировать неявну функцію: 7 кроків

Коли вам дана явна функція, у якій залежна змінна відокремлена на одній стороні від знака рівності (наприклад, y = x2 -3x), то ви запросто можете продифференцировать її (тобто знайти її похідну). Але неявні функції (наприклад, x2 + y2 - 5X + 8y + 2XY2 = 19), в яких відокремити залежну змінну не так просто, диференціюють по іншому.

Метод1 З 2:
Знаходження похідної простої функції

  1. На обох сторонах функції знайдіть (стандартним способом) похідні членів, що містять незалежну змінну «х», і похідні вільних членів. на цьому етапі члени, що містять залежну змінну «у», Поки не чіпайте. Наприклад, дана функція x2 + y2 - 5x + 8y + 2XY2 = 19.
    • У нашому прикладі x2 + y2 - 5x + 8y + 2XY2 = 19 Є два члени зі змінною «х": x2 і - 5x. знайдіть їх похідні:
      x2 + y2 - 5x + 8y + 2xy2 = 19
      (показник ступеня 2 в x2 зробіть множником, в-5x позбудьтеся від «х", а похідна 19 дорівнює 0)
      2x + y2 - 5 + 8y + 2xy2 = 0
  2. Тепер візьміть похідні від членів зі змінною " у " і припишіть до них (dy/dx).наприклад, при знаходженні похідної члена y2 запишіть її так: 2y(dy / dx). На цьому етапі члени, що містять обидві змінні (»х «і» у"), Поки не чіпайте.
    • У нашому прикладі 2x + y2 - 5 + 8y + 2XY2 = 0 продифференцируйте члени y2 і 8y:
      2x + y2 - 5 + 8y + 2xy2 = 0
      (показник ступеня 2 в у2 зробіть множником, а в 8у позбудьтеся від «у"; потім припишіть до отриманих похідних dx / dy)
      2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2xy2= 0
  3. Для знаходження похідної члена, що містить добуток двох змінних («х» та «у»), скористайтеся правилом диференціювання добутку функцій: (f × g)' = f' × g + g × f', де замість f підставте «х», а замість g – «у».[1] з іншого боку, для знаходження похідної члена, що містить ПРИВАТНЕ двох змінних («х» і «у»), скористайтеся правилом диференціювання приватного функцій: (f/g)' = (g X f' - g' X f)/g2, де замість f підставте «х», а замість g – «у» (або навпаки в залежності від даної вам функції).[2]
    • У нашому прикладі 2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2x2 = 0 є один член з обома змінними: 2XY2. Так як тут змінні перемножуються, скористайтеся правилом диференціювання добутку функцій:
      2XY2 = (2x)(y2) - нехай 2x = f і y2 = g в (f x g)' = f 'x g + g x f'
      (f × g)' = (2x)' × (y2) + (2x) × (y2)'
      (f × g)' = (2) × (y2) + (2x) × (2y(dy/dx))
      (f × g)' = 2y2 + 4xy(dy/dx)
    • Додайте ці члени до основної функції та отримайте:2x + 2Y(dy/dx) - 5 + 8(dy/dx) + 2y2 + 4xy(dy/dx) = 0
  4. Обособьте (dy/dx). майте на увазі, що будь-які два члени «а» і «b», які множаться на (dy/dx), можна записати у вигляді (a + b)(dy/dx).[3] для відокремлення (dy/dx) перенесіть всі члени без (dy/dx) на одну сторону від знака рівності, а потім розділіть їх на Члени, що стоять в дужках у (dy/dx).
    • У нашому прикладі 2x + 2Y(dy/dx) - 5 + 8(dy/dx) + 2Y2 + 4xy(dy/dx) = 0:
      2x + 2y(dy/dx) - 5 + 8(dy/dx) + 2y2 + 4xy(dy/dx) = 0
      (2y + 8 + 4xy)(dy/dx) + 2x - 5 + 2y2 = 0
      (2y + 8 + 4xy)(dy/dx) = -2y2 - 2x + 5
      (dy/dx) = (-2y2 - 2x + 5)/(2y + 8 + 4xy)
      (dy/dx) = (-2y2 - 2x + 5)/(2(2xy + y + 4)

Метод2 З 2:
Просунуті методи

  1. Підставте значення (x, y), щоб знайти (dy/dx) для будь-якої точки.відокремивши (dy/dx), Ви знайшли похідну неявної функції. Використовуючи цю похідну,ви можете знайти кутовий коефіцієнт дотичної в будь-якій точці (х, у), просто підставивши в знайдену похідну координати «х» і «у».
    • Наприклад, необхідно знайти кутовий коефіцієнт дотичної в точці А (3, -4). Для цього в похідну замість " х "підставте 3, а замість" у» підставте -4:
      (dy/dx) = (-2y2 - 2x + 5)/(2(2xy + y + 4)
      (dy/dx) = (-2(-4)2 - 2(3) + 5)/(2(2(3)(-4) + (-4) + 4)
      (dy/dx) = (-2(16) - 6 + 5)/(2(2(3)(-4))
      (dy/dx) = (-32) - 6 + 5)/(2(2(-12))
      (dy/dx) = (-33)/(2(2(-12))
      (dy/dx) = (-33)/(-48) = 3/48 = 0,6875.
  2. Скористайтеся ланцюговим правилом диференціювання складних функцій: якщо функцію F(x) можна записати у вигляді (fO g)(x), похідна F(x) дорівнюєF'(g(x))g'(x). Це означає, що похідну композиції двох і більше функцій можна обчислити на основі індивідуальних похідних.
    • Приклад: знайдіть похідну sin (3x2 + x). У цьому випадку позначимо sin(3x2 + x) як "f(x)" і 3x2 + x як "g (x)".
      f'(g(x))g'(x)
      (sin(3x2 + x))' × (3x2 + x)'
      cos(3x2 + x) × (6x + 1)
      (6x + 1)cos(3x2 + x)
  3. Якщо функція містить змінні «х», «у», «z», знайдіть (dz/dx)і (dz/dy).тобто якщо функція містить більше двох змінних, для кожної додаткової змінної необхідно знайти додаткову похідну по "х". Наприклад, якщо функція містить змінні "х», «у», "z", потрібно знайти (dz/dx) і (dz/dy). Ви можете зробити це, продифференцировав функцію по «х» двічі – в перший раз допишіть (dz/dx) у кожного продифференцированного члена з «z», а вдруге допишіть (dz/dy) при диференціюванні «z». Після цього просто відокремте (dz/dx) і (dz/dy).
    • Наприклад, знайдіть похідну x3z2 - 5XY5z = x2 + y3.
    • По-перше, продифференцируйте по " х " і допишіть (dz/dx). Не забудьте застосувати правило знаходження похідної добутку функцій.
      x3z2 - 5xy5z = x2 + y3
      3x2z2 + 2x3z(dz/dx) - 5y5z - 5xy5(dz/dx) = 2x
      3x2z2 + (2x3z - 5xy5)(dz/dx) - 5y5z = 2x
      (2x3z - 5xy5)(dz/dx) = 2x - 3x2z2 + 5y5z
      (dz/dx) = (2x - 3x2z2 + 5y5z)/(2x3z - 5xy5)
    • Тепер виконайте те ж саме для (dz / dy):
      x3z2 - 5xy5z = x2 + y3
      2x3z(dz/dy) - 25xy4z - 5xy5(dz/dy) = 3y2
      (2x3z - 5xy5)(dz/dy) = 3y2 + 25xy4z
      (dz/dy) = (3y2 + 25xy4z)/(2x3z - 5xy5)

Попередження

  • Звертайте увагу на Члени, при диференціюванні яких необхідно застосовувати правило знаходження похідної добутку або приватного функцій.

Джерела

  1. ↑ Https://www.math.hmc.edu/calculus/tutorials/prodrule/
  2. ↑ Https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/quotientruledirectory/QuotientRule.html
  3. ↑ Http://coolmath.com/prealgebra/06-properties/05-properties-distributive-01.htm

Ще почитати: