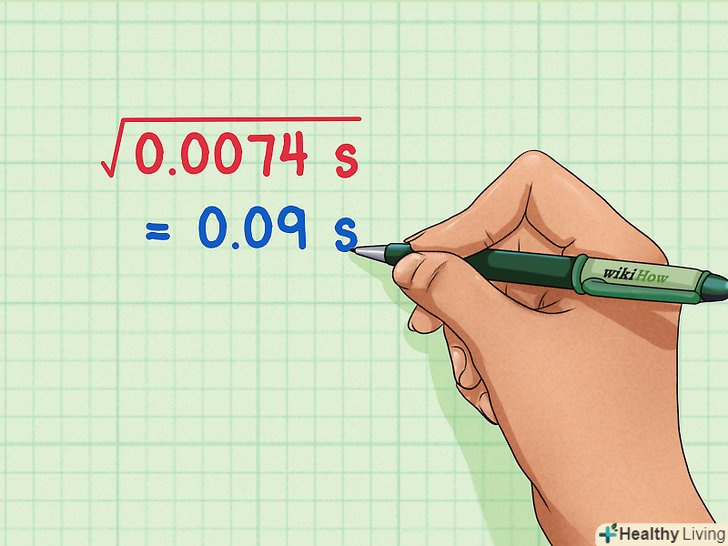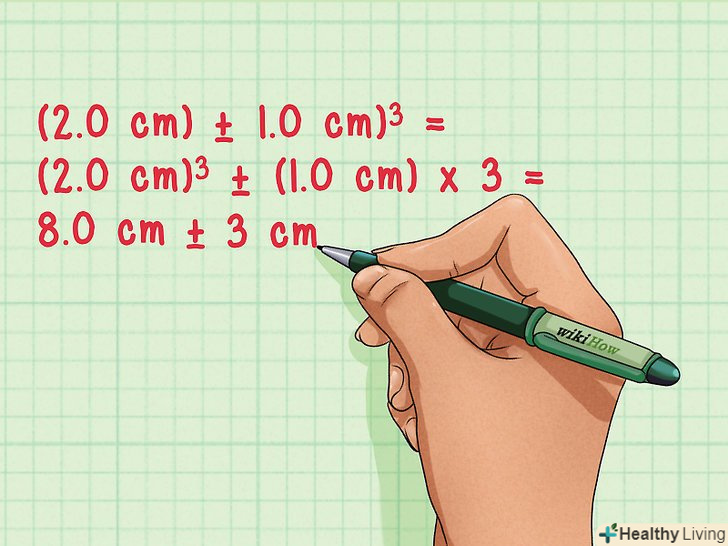1. Головна
    2. Математика
    3. Як знайти похибку-

Як знайти похибку-

При вимірюванні чого - небудь можна припустити, що є деяке "справжнє значення", яке лежить в межах діапазону значень, які ви знайшли. Для розрахунку більш точної величини потрібно взяти результат вимірювання і оцінити його при додаванні або відніманні похибки. Якщо ви хочете навчитися знаходити таку похибку, виконайте наступні дії.

Метод1З 3:
Основи

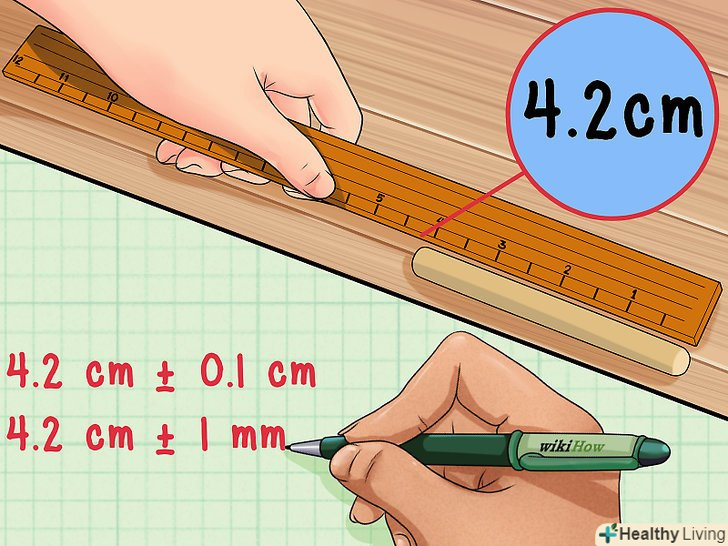
  1. Висловлюйте похибку правильно.припустимо, при вимірюванні палиці її довжина дорівнює 4,2 см плюс-мінус один міліметр. Це означає, що палиця приблизно дорівнює 4,2 см, але насправді може бути трохи менше або більше цього значення — з похибкою до одного міліметра.
    • Запишіть похибку як: 4,2 см ± 0,1 см. Ви також можете переписати це як 4,2 см ± 1 мм, так як 0,1 см = 1 мм.
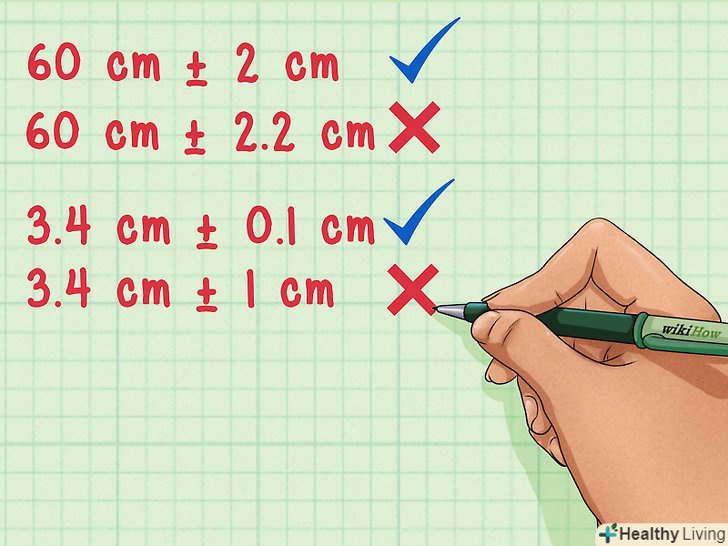
  2. Завжди округлюйте значення вимірювань до того ж знака після коми, що і в похибки.результати вимірювань, які враховують похибку, як правило, округлюються до однієї або двох значущих цифр. Найбільш важливим моментом є те, що потрібно округлити результати до того ж знака після коми, що і в похибки, щоб зберегти відповідність.
    • Якщо результат вимірювання 60 см, то і похибка слід округляти до цілого числа. Наприклад, похибка цього вимірювання може бути 60 см ± 2 см, але не 60 см ± 2,2 см.
    • Якщо результат вимірювання 3,4 см, то похибка округляється до 0,1 см. наприклад, похибка цього вимірювання може бути 3,4 см ± 0,7 см, але не 3,4 см ± 1 см.
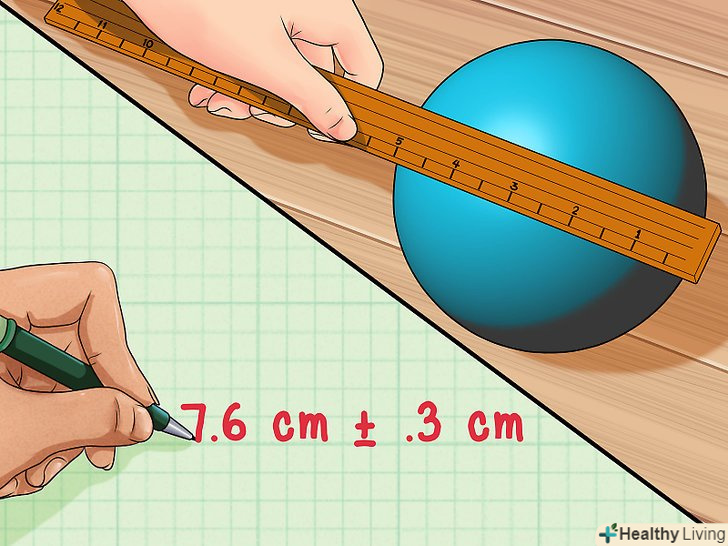
  3. Знайдіть похибку.Припустимо, ви вимірюєте лінійкою діаметр круглого кулі. Це складно, так як через кривизни кулі буде важко поміряти відстань між двома протилежними точками на його поверхні. Скажімо, лінійка може дати результат з точністю до 0,1 см, але це не означає, що ви можете виміряти діаметр з тією ж точністю.[1]
    • Вивчіть кулю і лінійку, щоб отримати уявлення про те, з якою точністю ви можете виміряти діаметр. У стандартної лінійки чітко видно розмітку по 0,5 см, але, можливо, ви зможете виміряти діаметр з більшою точністю, ніж ця. Якщо ви думаєте, що зможете виміряти діаметр з точністю до 0,3 см, то похибка в цьому випадку дорівнює 0,3 см.
    • Виміряємо діаметр кулі. Припустимо, ви отримали результат близько 7,6 см.Просто вкажіть результат вимірювання разом з похибкою. Діаметр кулі становить 7,6 см ± 0,3 см.
  4. Розрахуйте похибку вимірювання одного предмета з декількох.Скажімо, вам дано 10 компакт-дисків( CD), при цьому розміри кожного однакові. Припустимо, ви хочете знайти товщину всього одного CD. Ця величина настільки мала, що похибка практично неможливо обчислити. Проте, щоб обчислити товщину (і її похибка) одного CD, Ви можете просто розділити результат вимірювання (і його похибка) товщини всіх 10 CD, складених разом (один на іншого), на загальну кількість CD.[2]
    • Припустимо, що точність вимірювання стопки CD за допомогою лінійки 0,2 см. отже, ваша похибка ± 0,2 см.
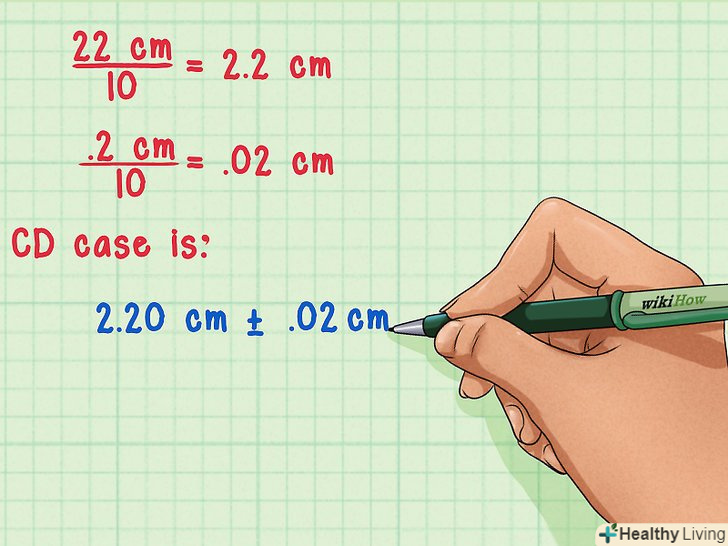
    • Припустимо, товщина всіх CD дорівнює 22 см.
    • Тепер розділимо результат вимірювання і похибка на 10 (число всіх CD). 22 см/10 = 2,2 см і 0,2 см/10 = 0,02 см. це означає, що товщина одного компакт-диска 2,20 см ± 0,02 см.
  5. Виміряйте кілька разів. для підвищення точності вимірювань, будь то вимірювання довжини або часу, заміряйте шукану величину кілька разів. Обчислення середнього значення з отриманих значень збільшить точність вимірювання і розрахунку похибки.

Метод2 З 3:
Обчислення похибки множинних вимірювань

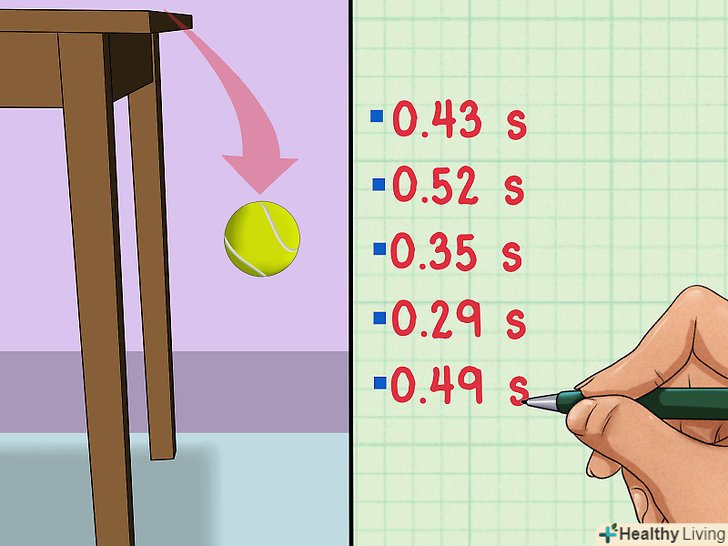
  1. Проведіть кілька вимірювань.Припустимо, ви хочете знайти, скільки часу падає м'яч з висоти столу. Щоб отримати найкращі результати, виміряйте час падіння наскільки разів, наприклад, п'ять. Потім потрібно знайти середнє значення з п'яти отриманих значень вимірювань часу, а потім для найкращого результату додати або відняти середньоквадратичне відхилення.[3]
    • Припустимо, в результаті п'яти вимірювань отримані результати: 0,43 с, 0,52 с, 0,35 с, 0,29 С і 0,49 с .
  2. Знайдіть середнє арифметичне.тепер знайдіть середнє арифметичне шляхом підсумовування п'яти різних результатів вимірювань і розділивши результат на 5 (кількість вимірювань). 0,43 + 0,52 + 0,35 + 0,29 + 0,49 = 2,08 с. 2,08 / 5 = 0,42 с. середній час 0,42 с.
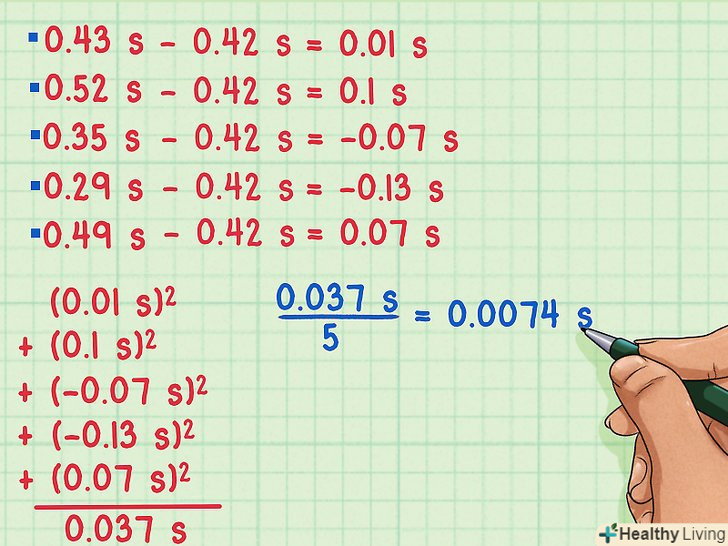
  3. Знайдіть дисперсію отриманих значень .для цього, по-перше, знайдіть різницю між кожною з п'яти величин і середнім арифметичним. Щоб зробити це, відніміть з кожного результату 0,42 с.[4]
      • 0,43 с-0,42 с = 0,01 с
      • 0,52 с-0,42 с = 0,1 с
      • 0,35 с-0,42 с = -0,07 с
      • 0,29 с-0,42 с = -0,13 с
      • 0,49 с-0,42 с = 0,07 с
      • Тепер складіть квадрати цих різниць: (0,01) 2 + (0,1) 2 +(-0,07) 2 +(-0,13) 2 + (0,07) 2 = 0,037 с.
      • Знайти середнє арифметичне цієї суми можна, розділивши її на 5: 0,037 / 5 = 0,0074 с.
  4. Знайдіть середньоквадратичне відхилення. щоб знайти середньоквадратичне відхилення, просто візьміть квадратний корінь з середнього арифметичного суми квадратів. Квадратний корінь з 0,0074 = 0,09 с, так що середньоквадратичне відхилення дорівнює 0,09 с.[5]
  5. Запишіть остаточну відповідь. щоб зробити це, запишіть середнє значення всіх вимірювань плюс-мінус середньоквадратичне відхилення. Оскільки середнє значення всіх вимірювань дорівнює 0,42 с, а середньоквадратичне відхилення 0,09 с, то остаточна відповідь 0,42 с ± 0,09 с.

Метод3 З 3:
Арифметичні дії з похибками

  1. Додавання . щоб скласти величини з похибками, складіть окремо величини і окремо похибки.[6]
    • (5 см ± 0,2 см) + (3 см ± 0,1 см) =
    • (5 см + 3 см) ± (0,2 см + 0,1 см) =
    • 8 см ± 0,3 см
  2. Віднімання. щоб відняти величини з похибками, відніміть величини і складіть похибки.[7]
    • (10 см ± 0,4 см) - (3 см ± 0,2 см) =
    • (10 см - 3 см) ± (0,4 см + 0,2 см) =
    • 7 см ± 0,6 см
  3. Множення. щоб помножити величини з похибками, перемножте величини і складіть відносні похибки (у відсотках).[8] розрахувати можна тільки відносну похибку, а не абсолютну, як і у випадку зі складанням і відніманням. Щоб дізнатися відносну похибку, розділіть абсолютну похибку на виміряне значення, потім помножте на 100, щоб висловити результат у відсотках. Наприклад:
    • (6 см ± 0,2 см) = (0,2 / 6) x 100 — додавши знак відсотка, отримуємо 3,3 %.
      отже:
    • (6 см ± 0,2 см) х (4 см ± 0,3 см) = (6 см ± 3,3%) x (4 см ± 7,5 %)
    • (6 см x 4 см) ± (3,3 + 7,5) =
    • 24 см ± 10,8% = 24 см ± 2,6 см
  4. Поділ. щоб розділити величини з похибками, розділіть величини і складіть відносні похибки.[9]
    • (10 см ± 0,6 см) ÷ (5 см ± 0,2 см) = (10 см ± 6%) ÷ (5 см ± 4%)
    • (10 см ÷ 5 см) ± (6 % + 4 %) =
    • 2 см ± 10 % = 2 см ± 0,2 см
  5. Зведення в ступінь. для того, щоб звести в ступінь величину з похибкою, зведіть величину в ступінь, а відносну похибку помножте на ступінь.[10]
    • (2,0 см ± 1,0 см)3 =
    • (2,0 см)3 ± (50 %) x 3 =
    • 8,0 см3 ± 150% або 8,0 см3 ±12 см3

Поради

  • Ви можете дати похибку як для загального результату всіх вимірювань, так і для кожного результату одного вимірювання окремо. Як правило, дані, отримані з декількох вимірювань, менш достовірні, ніж дані, отримані безпосередньо з окремих вимірювань.

Попередження

  • Точні науки ніколи не працюють з» істинними " величинами. Хоча правильне вимірювання, швидше за все, дасть величину в межах похибки, немає ніякої гарантії, що це буде так. Наукові вимірювання допускають можливість помилок.
  • Похибки, описані тут, застосовні тільки для випадків нормального розподілу (розподілу Гауса). Інші розподіли ймовірностей вимагають інших рішень.

Джерела

  1. ↑ Http://www2.southeastern.edu/Academics/Faculty/rallain/plab194/error.html
  2. ↑ Http://www2.southeastern.edu/Academics/Faculty/rallain/plab194/error.html
  3. ↑ Http://www2.southeastern.edu/Academics/Faculty/rallain/plab194/error.html
  4. ↑ Http://www.mathsisfun.com/data/standard-deviation.html
  5. ↑ Http://www.mathsisfun.com/data/standard-deviation.html
  6. ↑ Http://web.uvic.ca/~jalexndr/192UncertRules.pdf
  7. ↑ Http://web.uvic.ca/~jalexndr/192UncertRules.pdf
  8. ↑ Http://web.uvic.ca/~jalexndr/192UncertRules.pdf
  9. ↑ Http://web.uvic.ca/~jalexndr/192UncertRules.pdf
  1. ↑ Http://web.uvic.ca/~jalexndr/192UncertRules.pdf

Ще почитати: