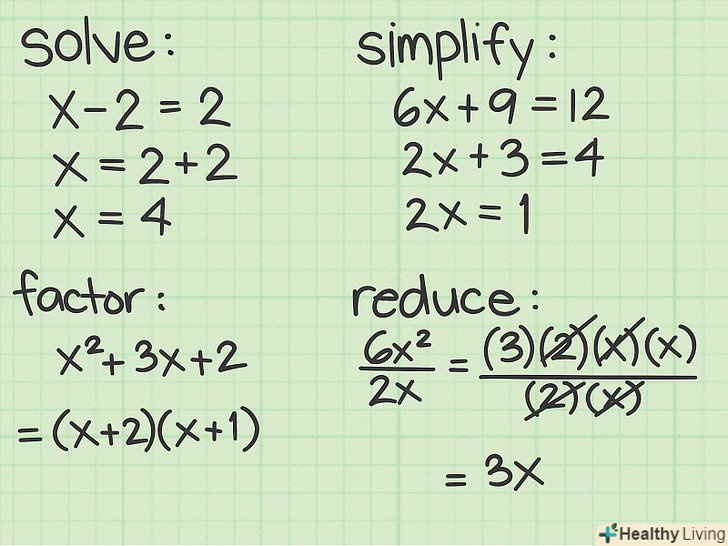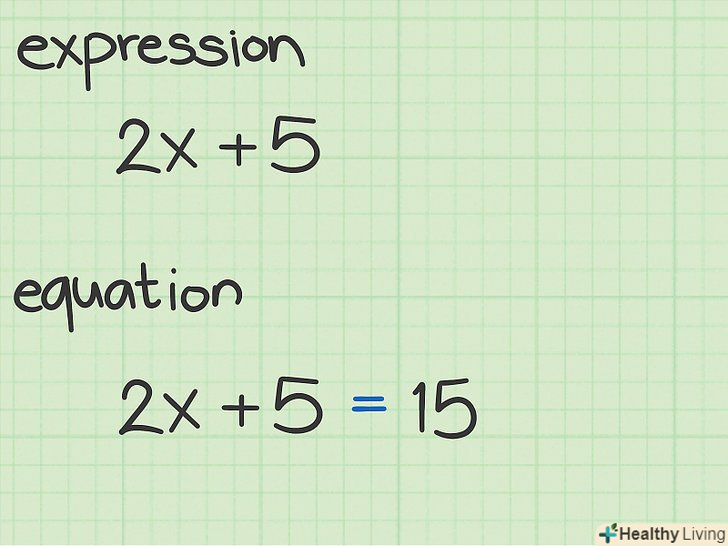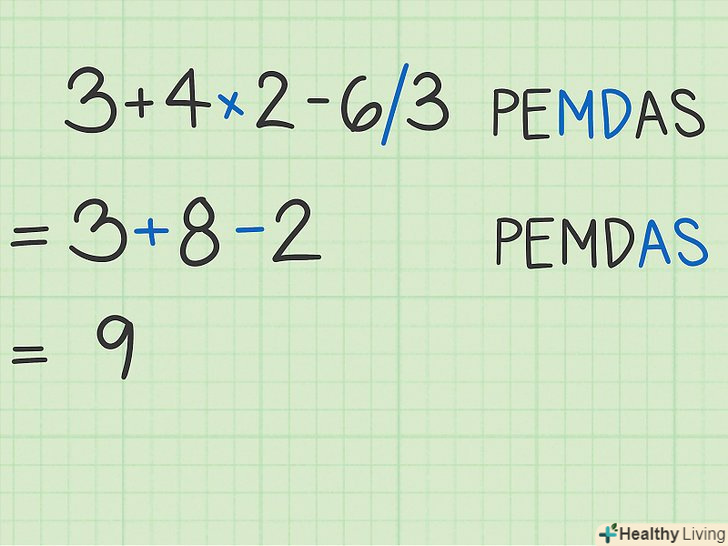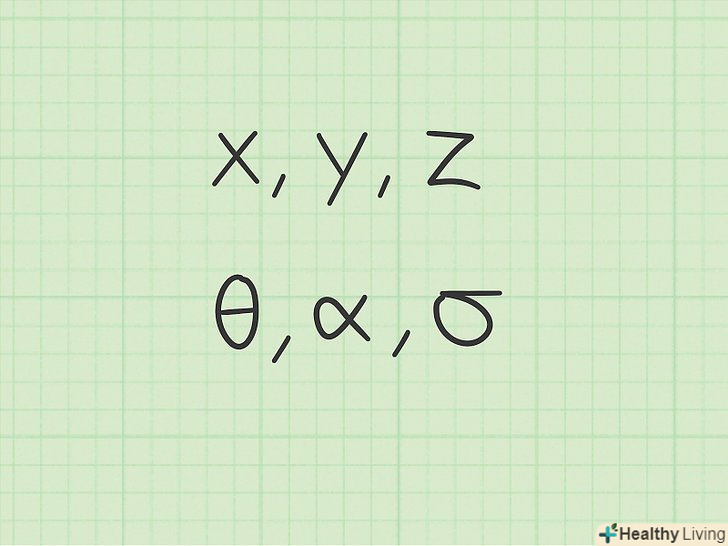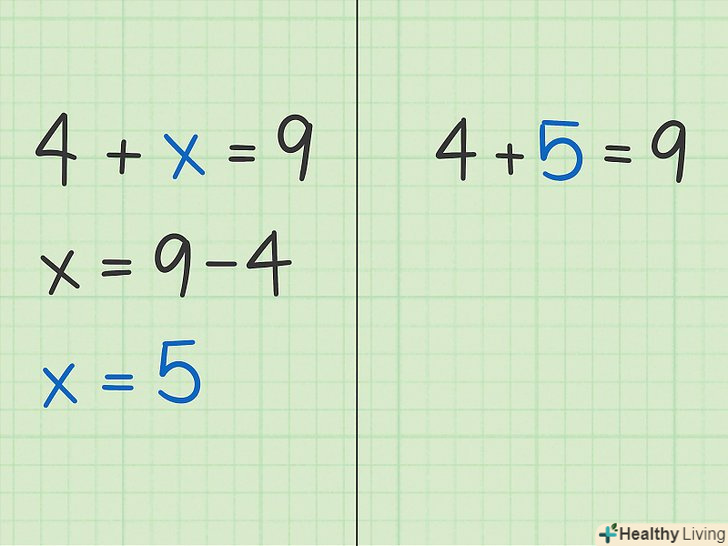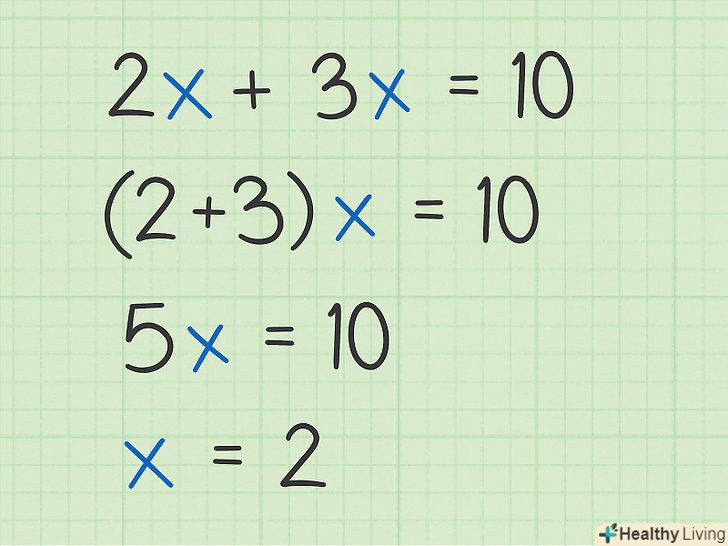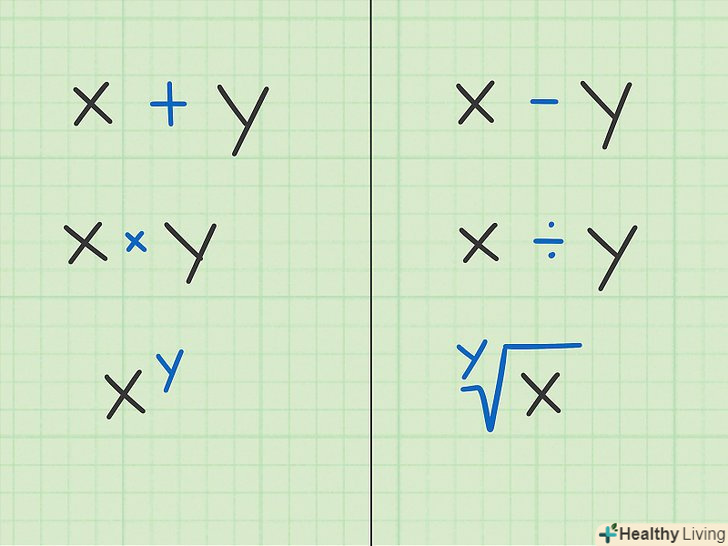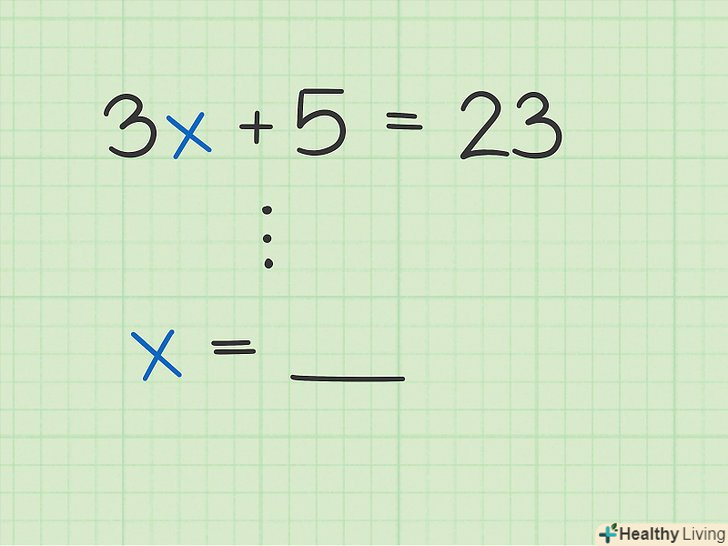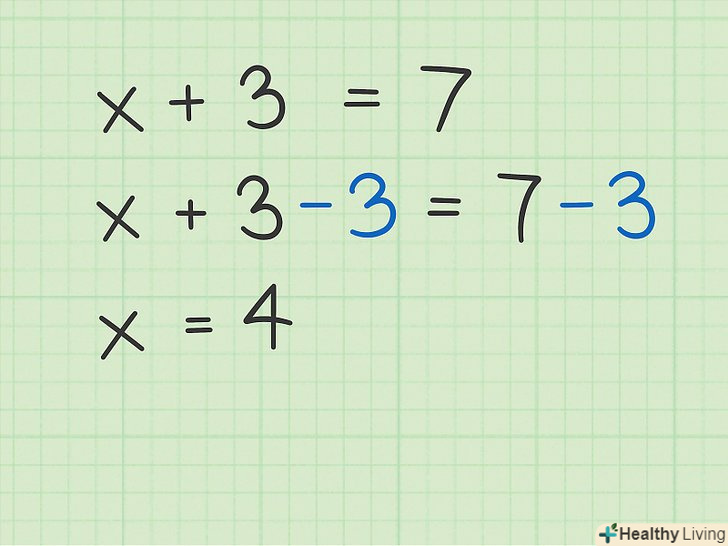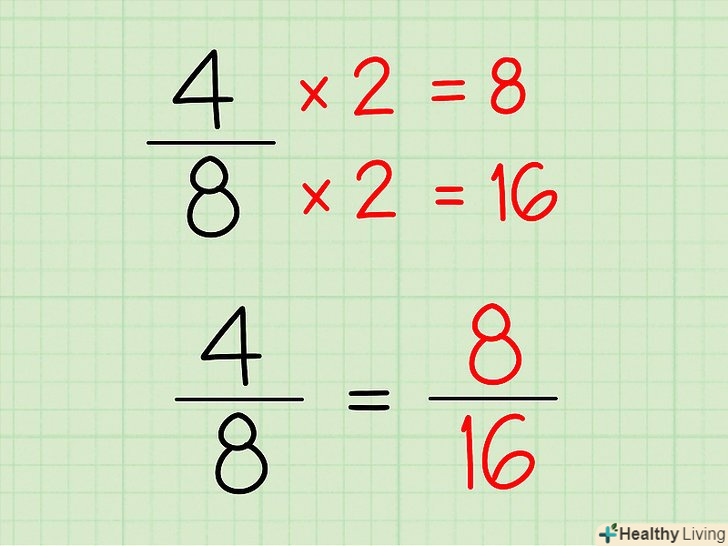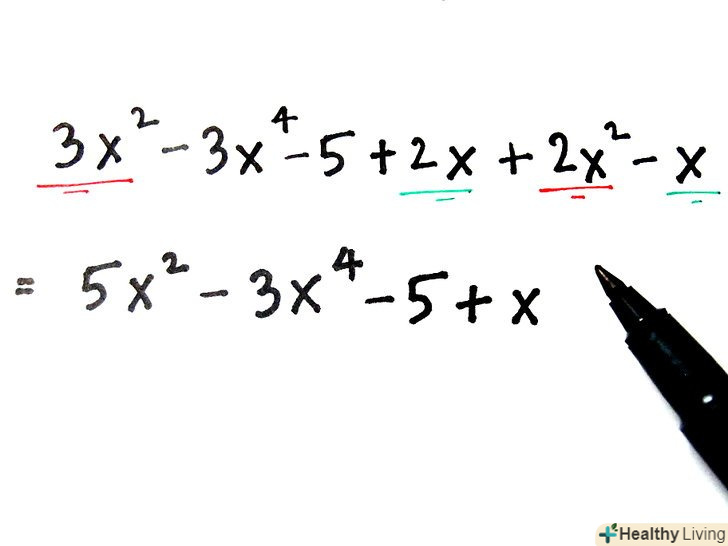1. Головна
    2. Математика
    3. Як зрозуміти алгебру (з ілюстраціями)

Як зрозуміти алгебру (з ілюстраціями)

Спочатку алгебра може здатися складним предметом. Але якщо створити базу початкових математичних знань і вивчити деякі алгебраїчні поняття, цей предмет дасться вам набагато легше. Щоб вирішити будь-яку алгебраїчну задачу, потрібно виконати ряд послідовних нескладних операцій. При цьому вихідна задача приводиться до такого виду, що її дуже легко вирішити.

Частина1З 5:
Визначення цілей

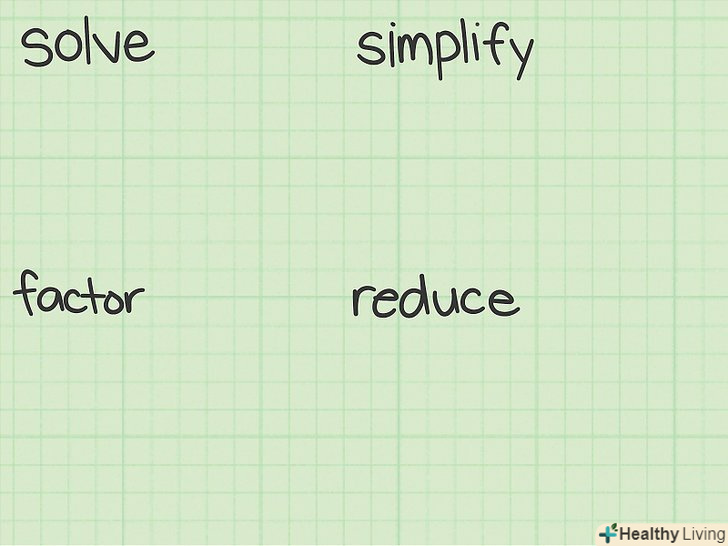
  1. Уважно прочитайте умову задачі.необхідно з'ясувати, що потрібно зробити в даній задачі. Зверніть увагу на ключові слова "вирішити», «спростити», «розкласти»або "скоротити". Ці слова найчастіше зустрічаються в умовах завдань (хоча є й інші). Пам'ятайте, що не потрібно» вирішувати "завдання, якщо потрібно "спростити" її.[1]
  2. Виконайте відповідні дії.за ключовими словами в умові завдання можна визначити, які дії потрібно виконати. Не витрачайте час на дії, які не потрібно виконувати в даній задачі. Основними діями є: [2]
    • Вирішити. Тут необхідно знайти фактичне чисельне рішення, наприклад, значення змінної x=4.
    • Спростити. Тут вихідне рівняння (або нерівність) потрібно переписати в більш простій формі, але чисельне рішення (значення змінної) знаходити не потрібно.
    • Розкласти на множники. Ця дія аналогічна «спрощенню " і зазвичай застосовується до складних многочленів і дробів. Тут алгебраїчний вираз (або число) потрібно розкласти на ряд множників. Наприклад, число 12 можна розкласти на множники 3x4; аналогічно на множники можна розкласти алгебраїчний многочлен.
      • Наприклад, вираз5x{\displaystyle 5x} можна розкласти на множники і .
      • Наприклад, виразX2+3x+2{\displaystyle x^{2}+3x+2} можна розкласти на множники і .
    • Скоротити. Тут потрібно позбутися від деяких членів виразу, щоб записати вихідний вираз в більш простому вигляді. Скорочення включає в себе розкладання на множники і спрощення. Потрібно розкласти на множники чисельник і знаменник дробу. Потім знайти однакові члени в чисельнику і знаменники і скоротити їх. Отриманий вираз буде "скороченою" формою вихідного виразу. Наприклад, скоротіть вираз6x22x{\displaystyle {\frac {6x^{2}}{2x}}} наступним чином:
      • 1. Розкладіть на множники чисельник і знаменник:(3)(2)(x)(x)(2)(x){\displaystyle {\frac {(3)(2)(x)(x)}{(2)(x)}}}
      • 2. Знайдіть однакові члени. У чисельнику і знаменнику присутні "2»і "x".
      • 3. Скоротіть однакові члени:(3)(2)(x)(x)(2)(x){\displaystyle {\frac {(3)(2)(x)(x)}{(2)(x)}}}
      • 4. Запишіть скорочену вираз:
  3. Запам'ятайте різницю між "виразом»і "рівнянням".в алгебрі різниця між "виразом" і» рівнянням " досить істотна. Вираз являє собою будь-яку групу чисел і змінних, пов'язаних математичними операціями. Деякі приклади виразів: X2{\displaystyle x^{2}}, і . Вираз можна розкласти на множники, спростити, скоротити, але не вирішити. Рівняння обов'язково включає знак рівності»=". Рівняння можна розкласти на множники, спростити, скоротити і вирішити, тобто отримати чисельне рішення.[3]
    • Наприклад, якщо дано вираз4x2{\displaystyle 4x^{2}}, ви не отримаєте єдине чисельне рішення. Ви могли б знайти, що якщо , то вираз дорівнює 4, а якщо , то вираз дорівнює (4)(2)2{\displaystyle (4)(2)^{2}} = 16. Але єдиного рішення (відповіді) не буде.

Частина2З 5:
Порядок операцій

  1. Запам'ятайте правильний порядок виконання математичних операцій.в алгебрі абсолютно всі математичні операції виконуються в певному порядку. Ось він:[4]
    • Дія в дужках;
    • Зведення в ступінь;
    • Множення;
    • Поділ;
    • Додавання;
    • Віднімання.
  2. Спочатку виконайте операції всередині дужок.якщо дано вираз або рівняння, деякі члени якого укладені в дужки, спочатку потрібно виконати операції всередині дужок. Розглянемо різницю між виразами 5∗3+2{\displaystyle 5*3+2} і .[5]
    • Перший вираз (без дужок):5∗3+2{\displaystyle 5*3+2} = .
    • Другий вираз (з дужками): = (тут спочатку складаємо 3+2=5).
  3. Далі зведіть в ступінь.зведення в ступінь-це другий крок в правильному порядку операцій. Наприклад, дано вираз3∗22{\displaystyle 3*2^{2}}. Якщо не слідувати порядку операцій, то спочатку потрібно перемножити: 3∗2=6{\displaystyle 3*2=6}, а потім звести в квадрат: 6^2=36, але так ви отримаєте неправильний результат. Ось як знайти правильне рішення: [6]
    • (спочатку зведіть в квадрат).
    • (це правильний результат).
  4. Помножте або розділіть, починаючи зліва. коли ви зведете щось в ступінь, виконайте операції множення і ділення; почніть з лівого боку виразу.[7]
    • , де 4 * 2=8 і 6/3=2.
  5. Складіть або відніміть, починаючи зліва.Все, що залишилося зробити-відняти або скласти члени виразу; почніть з лівого боку виразу. Наприклад, дано вираз .[8]
    • (склали 4+2)
    • (відняли 6-3)
    • (відняли 3-1)
    • (відняли 2-5)
    • (склали -3+2)
    • Якщо виконати операції в іншому порядку, ви отримаєте невірний результат. Наприклад, припустимо, що спочатку ви все склали, а потім вирахували:
    • (склали 4+2 5+2)
    • (відняли 6-3)
    • (відняли 3-1)
    • (відняли 2-7. Отримали результат -5, який невірний)

Частина3З 5:
Робота зі змінними

  1. Використовуйте символи, відмінні від цифр.коли ви починали вивчати математику, ви працювали тільки з числами. В алгебрі потрібно вміти вирішувати рівняння з невідомими членами. У рівняннях невідомі члени представлені літерами, які називаються змінними. Ставтеся до таких букв як до чисел, хоча ви ще не знаєте їх фактичних значень. Ось найпоширеніші змінні: [9]
    • Латинські літери, такі як, і ;
    • Грецькі літери, такі як, і .
    • Деякі символи схожі на змінні, але насправді не є такими. Наприклад, грецька буква π позначає число Пі, значення якого відомо: 3,1415.
  2. Розглядайте змінну як невідоме число. наприклад, якщо сказано "два помножити на деяке число", це можна записати у вигляді виразу 2∗x{\displaystyle 2*x}. Змінна замінює невідоме число («деяке число»). У більшості алгебраїчних задач потрібно знайти значення змінної.[10]
    • Наприклад, дано рівняння4+x=9{\displaystyle 4+x=9}. Тут необхідно з'ясувати, яке число потрібно додати до 4, щоб отримати 9. Відповідь — число 5, що можна записати у вигляді .
  3. Наведіть (складіть або відніміть) подібні (однакові) члени (в даному випадку змінні).якщо розглядати змінні як числа, їх можна складати і віднімати. Така дія називається»приведенням подібних членів".[11]
    • Наприклад, дано рівняння2x+3x=10{\displaystyle 2x+3x=10}. У ньому дві змінні додаються до трьох таким же змінним, а все вираз дорівнює 10. Якщо у вас є два і три однакових предмета, їх можна скласти. У нашому прикладі 2x+3x{\displaystyle 2x+3x} = 5x, тому вихідне рівняння запишеться так: , а рішення так: .
    • Складати і віднімати можна тільки подібні (однакові) змінні. Пам'ятайте, що в деяких рівняннях є кілька різних змінних. Наприклад, у рівнянні2x+3y=10{\displaystyle 2x+3y=10} змінні і складати не можна, тому що вони різні, тобто є заміною різних невідомих чисел.

Частина4З 5:
Зворотні операції

  1. Запам'ятайте, що таке зворотна операція (зворотна дія).Зворотні операції відіграють велику роль в алгебрі. Зворотне означає протилежне. Зворотні дії дозволяють спростити завдання. Наприклад, якщо в задачі є операція множення, використовуйте ділення, яке є зворотним дією до множення, щоб вирішити задачу.[12]
    • Зворотна операція до додавання-віднімання.
    • Зворотна операція до віднімання-додавання.
    • Зворотна операція до множення-ділення.
    • Зворотна операція до ділення-множення.
    • Зворотна операція до зведення в ступінь-Витяг кореня (квадратного кореня, кубічного кореня і так далі).
  2. Ізолюйте змінну. якщо потрібно» вирішити "рівняння, це означає, що необхідно прийти до рівності X={\displaystyle x=}__, де замість пробілу варто число. Скористайтеся математичними операціями, щоб змінна X{\displaystyle x} залишилася на одній стороні рівняння, а всі інші члени — на іншій стороні рівняння. Це можна зробити за допомогою зворотних операцій.[13]
    • Запам'ятайте: будь-яка операція, яку ви виконуєте на одній стороні рівняння, повинна бути виконана і на іншій стороні. Тільки так значення вихідного рівняння не зміниться.

Ще почитати: