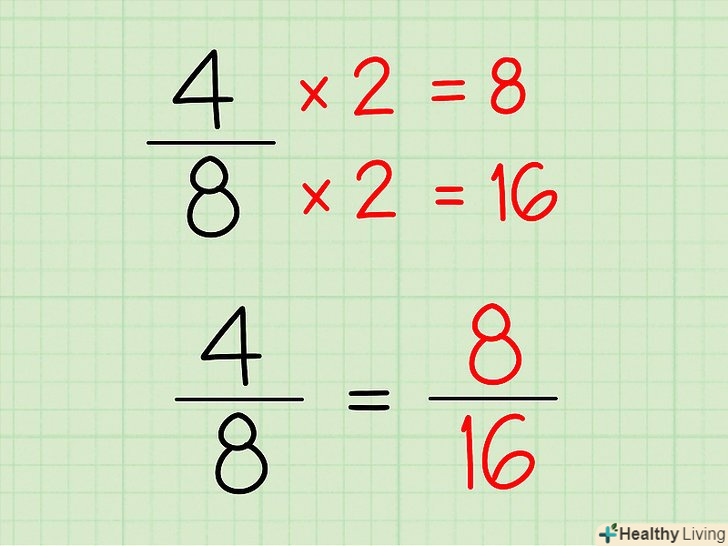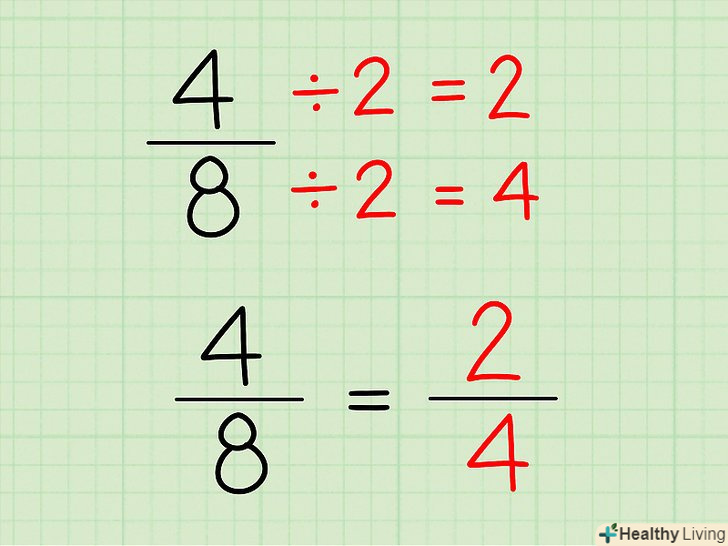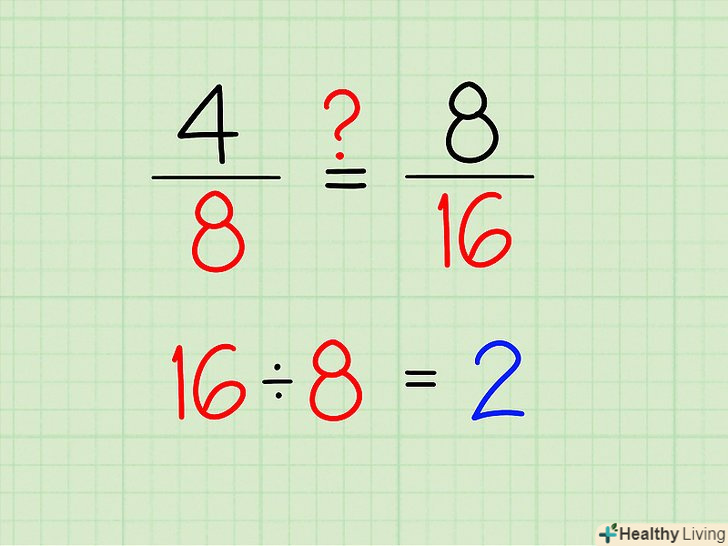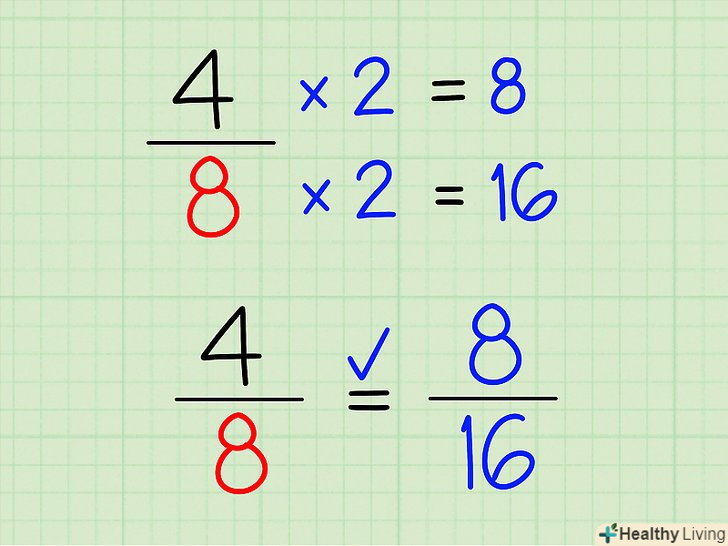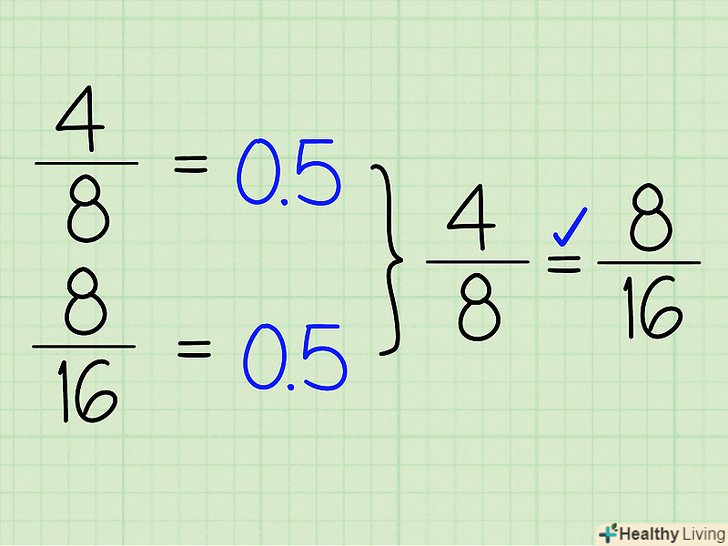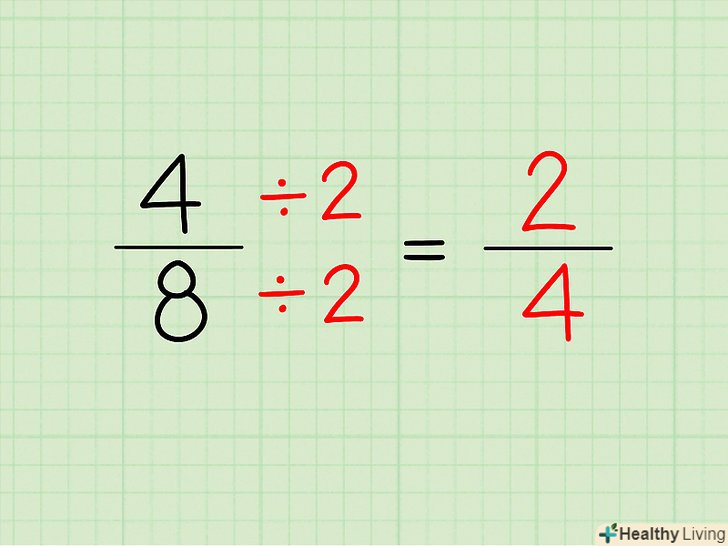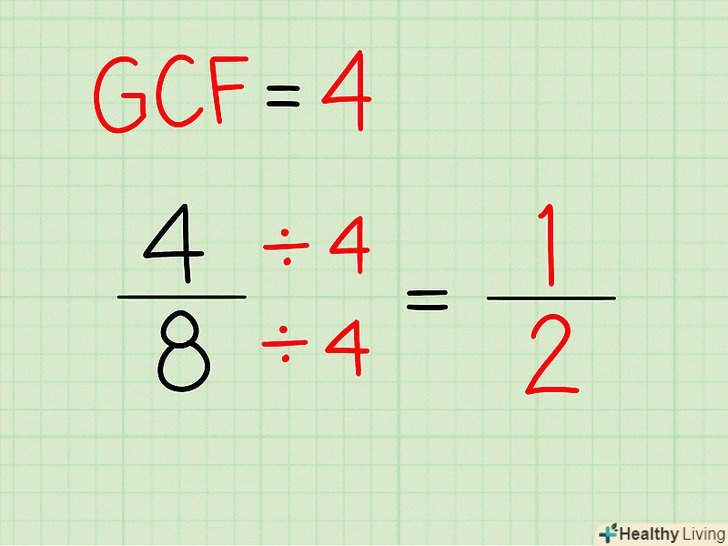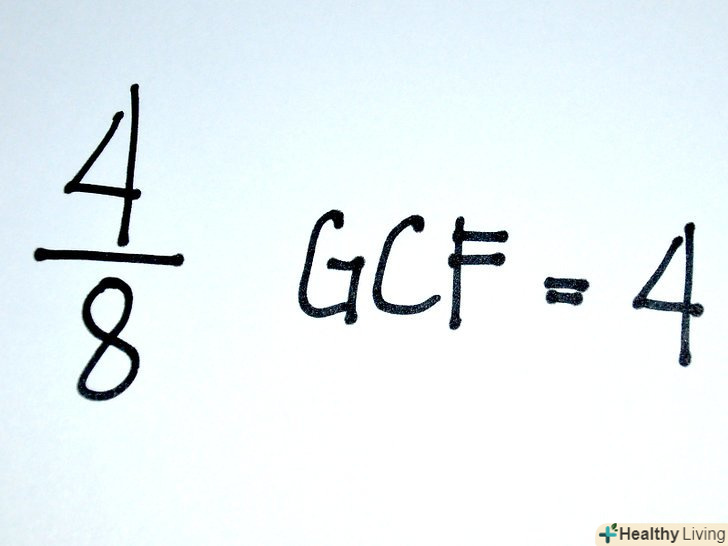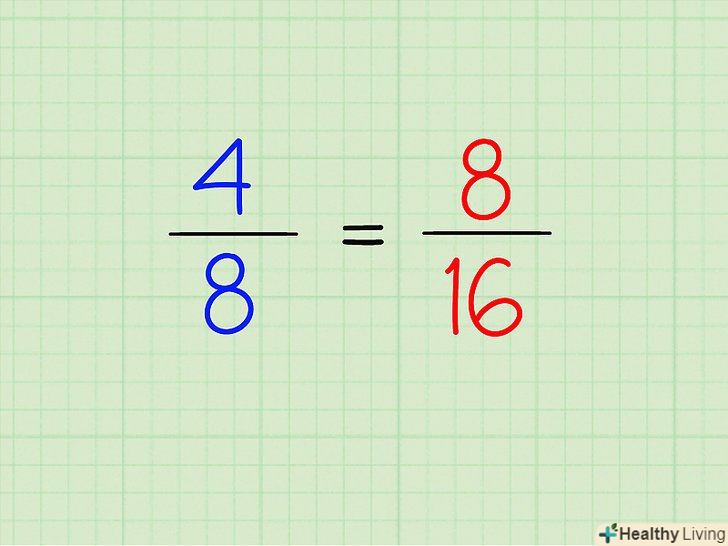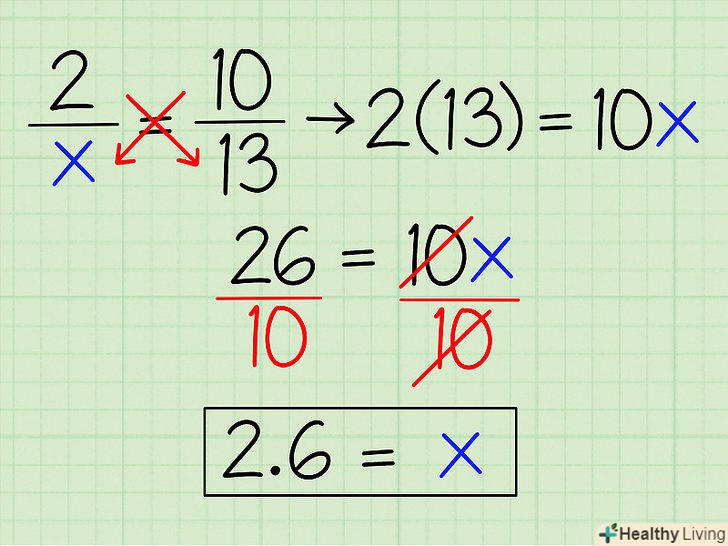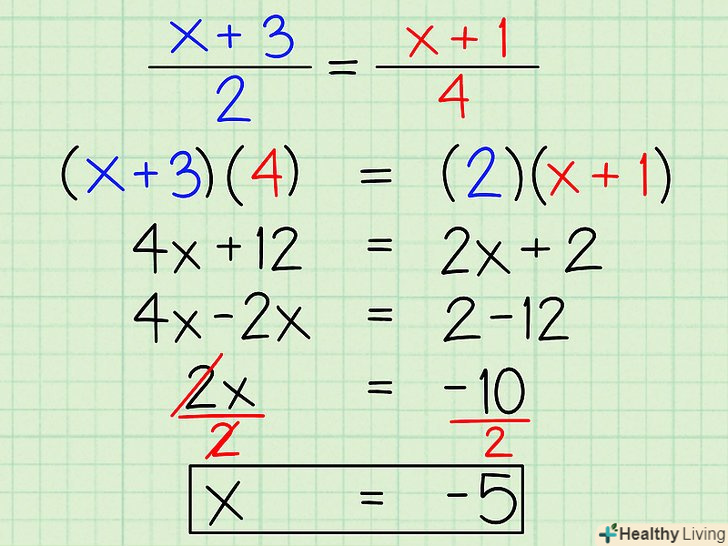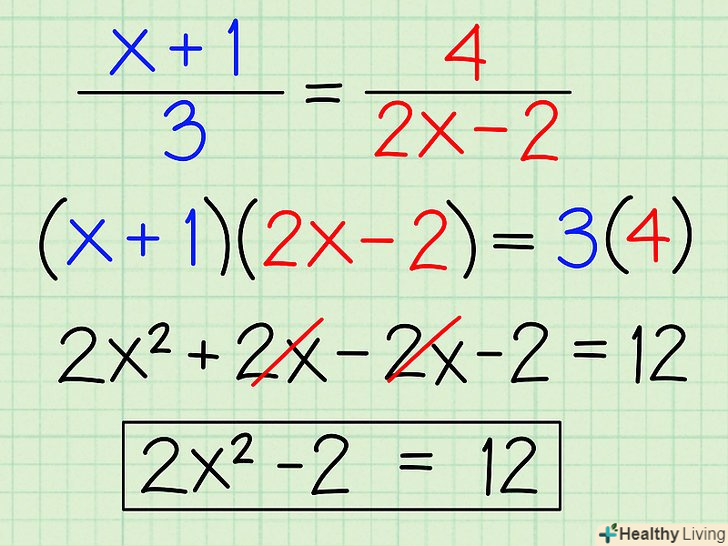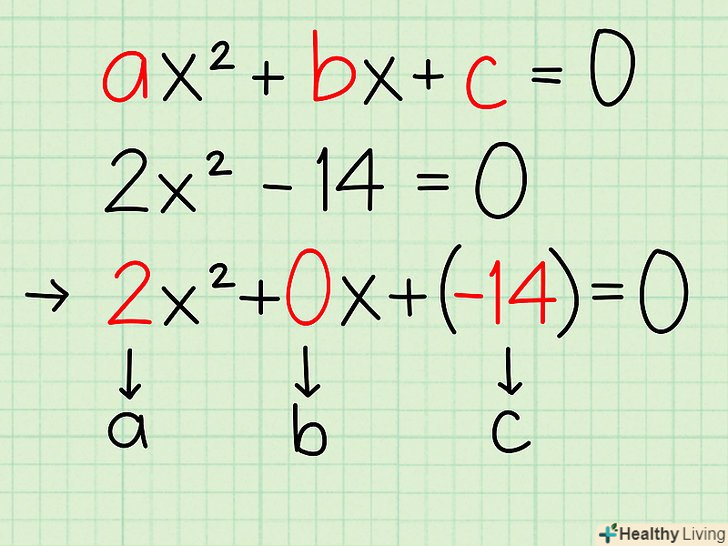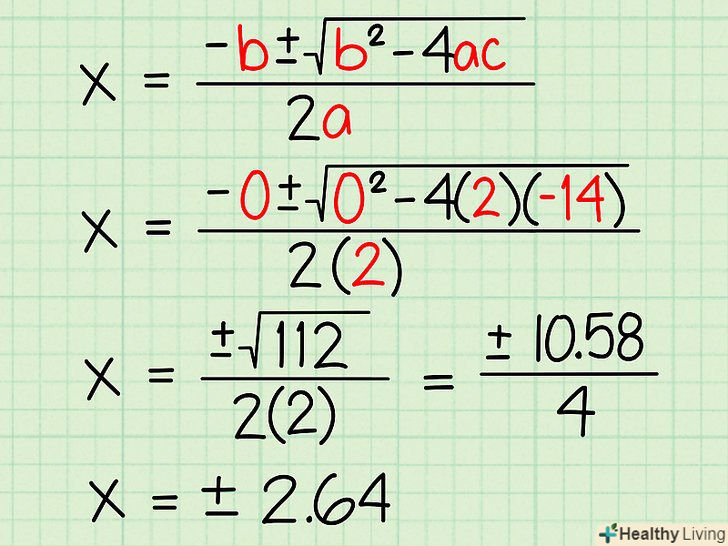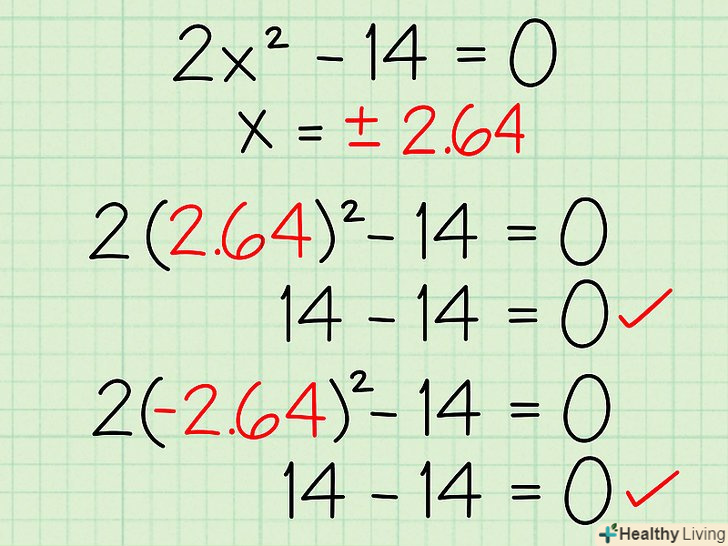1. Головна
    2. Математика
    3. Як працювати з еквівалентними дробами-

Як працювати з еквівалентними дробами-

Два дроби еквівалентні, якщо вони мають однакове значення. Дроби 1/2 і 2/4 еквівалентні, оскільки значення 1 ділити на 2 дорівнює значенню 2 ділити на 4 або 0,5 у вигляді десяткового дробу. Перетворення дробів в еквівалентні дроби корисно при проведенні звичайних і складних обчислень. Ця стаття розповість вам, як отримувати еквівалентні дроби через ділення і множення, а також про те, як вирішувати рівняння з еквівалентними дробами.

Метод1З 5:
Отримання еквівалентних дробів

  1. Помножте чисельник і знаменник на одне і те ж число. у двох еквівалентних дробів чисельники діляться один на одного націлено, і знаменники діляться один на одного націлено (при цьому ви повинні отримати одне число). Іншими словами, помноживши чисельник і знаменник будь-якої дробу на одне і те ж число, ви отримаєте еквівалентну дріб (значення вихідної і отриманої дробів будуть однаковими).
    • Наприклад, дана дріб 4/8. Помножте чисельник і знаменник на 2 і отримаєте: (4 × 2) / (8 × 2) = 8/16. Ці два дроби еквівалентні.
    • (4 × 2) / (8 × 2) = 4/8 × 2/2. Пам'ятайте, що при множенні двох дробів потрібно перемножити їх чисельники, а потім перемножити їх знаменники.
    • Зверніть увагу, що 2/2 = 1. Таким чином, 4/8 і 8/16 – це еквівалентні дроби, так як множачи 4/8 на 1 (2/2 = 1), значення дробу не змінюється. Тому 4/8 = 8/16.
    • Будь-який дріб має нескінченне число еквівалентних дробів. Ви можете помножити чисельник і знаменник на будь-яке ціле число, щоб отримати еквівалентну дріб.
  2. Розділіть чисельник і знаменник на одне і те ж число.аналогічно множенню, операція ділення також може бути використана для того, щоб отримати нову дріб, яка буде еквівалентна вихідної дробу. Для цього розділіть чисельник і знаменник на одне і те ж число (чисельник і знаменник повинні ділитися на це число без залишку, і в чисельнику і знаменнику повинні бути цілі числа).
    • Наприклад, дана дріб 4/8. Якщо замість множення ви розділите чисельник і знаменник на 2, то отримаєте: (4 ÷ 2) / (8 ÷ 2) = 2/4. 2 і 4 - цілі числа, тому дріб 2/4 еквівалентна дробу 4/8.

Метод2З 5:
Використання операції множення для визначення еквівалентності

  1. Якщо вам дано завдання на визначення еквівалентності двох дробів, то знайдіть число, на яке потрібно помножити менший знаменник, щоб отримати більший знаменник.так ви приведете дроби до спільного знаменника.
    • Наприклад, дані дроби 4/8 і 8/16. Менший знаменник 8 ви множите на 2 і отримуєте більший знаменник 16. Таким чином, шукане число в даному прикладі – це число 2.
    • Для полегшення знаходження потрібного числа просто розділіть більший знаменник на менший знаменник. У цьому випадку 16/8 = 2.
    • Число не обов'язково буде цілим. Наприклад, якщо знаменники рівні 2 і 7, то число дорівнює 3,5.
  2. Помножте чисельник і знаменник меншої дробу (з меншим знаменником) на знайдене число.якщо в результаті ви отримаєте великий дріб (з великим знаменником), то дані дробу еквівалентні.[1]
    • У нашому прикладі помножте менший дріб 4/8 на знайдене число 2: (4 х 2)/(8 х 2) = 8/16. Ви отримали велику дріб, тому дані дробу 4/8 і 8/16 є еквівалентними.

Метод3З 5:
Використання операції ділення для визначення еквівалентності

  1. Висловіть кожен дріб у вигляді десяткового дробу, щоб визначити їх еквівалентність.для цього просто розділіть чисельник дробу на її знаменник.
    • Наприклад, дані дроби 4/8 і 8/16. 4/8= 0,5; 8/16 = 0,5. Так як дві десяткові дроби рівні, то вихідні дроби еквівалентні.
    • Пам'ятайте, що в десятковому дробі після десяткової коми може стояти нескінченної число цифр. Це треба враховувати при визначенні еквівалентності. Наприклад, 1/3 = 0,333, а 3/10 = 0,3. Таким чином, дроби 1/3 і 3/10 не є еквівалентними.
  2. Розділіть чисельник і знаменник дробу на одне і те ж число, щоб отримати еквівалентну дріб.при цьому і в чисельнику, і в знаменнику повинні знаходитися цілі числа.
    • Наприклад, дана дріб 4/8. Якщо замість множення ви розділите чисельник і знаменник на 2, то отримаєте (4 ÷ 2)/(8 ÷ 2) = 2/4. 2 і 4 є цілими числами, тому дріб 2/4 еквівалентна дробу 4/8.
  3. Спростіть дріб, розділивши чисельник і знаменник на найбільший спільний дільник (НСД). це найбільше число, на яке можна розділити і чисельник і знаменник. Цей крок повинен привести два дроби до найменшого спільного знаменника (тільки якщо дроби еквівалентні).
    • При спрощенні дробу Ви отримаєте дріб з найменшими можливими чисельником і знаменником. Чисельник і знаменник не можуть бути розділені на будь-яке ціле число; їх необхідно ділити на їх НСД.
    • У нашому прикладі (дріб 4/8) НСД = 4, так як 4 – це найбільше число, яке ділить 4 і 8 без залишку. Щоб спростити дріб, розділіть чисельник і знаменник на 4: (4 ÷ 4)/(8 ÷ 4) = 1/2. Аналогічно, у випадку дробу 8/16 НСД = 8 і: (8 ÷ 8)/(16 ÷ 8) = 1/2.

Метод4З 5:
Використання множення навхрест для знаходження змінної

  1. Множення хрест-навхрест використовується в задачах з двома еквівалентними дробами, одне з чисел в яких замінено на змінну (зазвичай "х"»; цю змінну необхідно знайти.Так як дроби еквівалентні, то їх можна прирівняти (поставити між ними знак рівності) і знайти змінну за допомогою множення хрест-навхрест.[2]
  2. При множенні хрест-навхрест потрібно помножити чисельник першого дробу на знаменник другого дробу, а потім помножити чисельник другого дробу на знаменник першого дробу; між результатами перемноження поставте знак рівності. [3]
    • Наприклад, дано два дроби 4/8 і 8/16. Вони не містять змінну, але використовуємо множення хрест-навхрест, щоб перевірити їх еквівалентність: 4 х 16 = 8 х 8 або 64 = 64. Таким чином, ці дроби еквівалентні (якщо рівність не зберігається, то дроби не є еквівалентними).
  3. Введіть змінну в одну з еквівалентних дробів, щоб за допомогою множення хрест-навхрест знайти її.
    • Наприклад, розглянемо рівняння 2 / х = 10/13. Помножте 2 на 13 і 10 на «х», а потім прирівняйте результати один одному:
      • 2 × 13 = 26
      • 10 × x = 10x
      • 10x = 26. Розділіть обидві частини рівняння на 10 і отримаєте х = 26/10 = 2,6.
  4. Множення хрест-навхрест працює з будь-якими дробами, включаючи дроби зі складними виразами.наприклад, якщо обидві дроби містять змінні, в процесі обчислень їх необхідно скоротити; якщо ж чисельник або знаменник даних дробів містять вирази (наприклад, х + 1), то при множенні хрест-навхрест необхідно розкрити дужки (перемноживши число за дужками і кожен член виразу в дужках) і вирішити отримане рівняння стандартним способом.[4]
    • Наприклад, розглянемо рівняння ((х + 3)/2) = ((х + 1)/4).
      • (x + 3) × 4 = 4x + 12
      • (x + 1) × 2 = 2x + 2
      • 2x + 2 = 4x + 12. Перенесіть 2х на праву сторону рівняння.
      • 2 = 2x + 12. Тепер перенесіть 12 на ліву сторону рівняння.
      • -10 = 2x.розділіть на 2 обидві сторони рівняння.
      • -5 = х

Метод5З 5:
Використання формули для знаходження коренів квадратного рівняння

  1. Цей метод також починається з множення навхрест, яке може привести до того, що Ви отримаєте змінну в другому ступені (в квадраті).у таких випадках, можливо, буде потрібно використовувати такі методи, як розкладання квадратного рівняння на множники або рішення квадратного рівняння за допомогою формули.[5]
    • Наприклад, розглянемо рівняння ((x +1)/3) = (4/(2x-2)). Помножте хрест-навхрест:
      • (x + 1) × (2x - 2) = 2x2 + 2x -2x - 2 = 2x2 - 2
      • 4 × 3 = 12
      • 2x2 - 2 = 12.
  2. Висловіть отримане рівняння у вигляді квадратного рівняння (ax2 + bx + c = 0), прирівнявши рівняння до нуля. у нашому прикладі перенесіть 12 на ліву сторону рівняння і отримаєте 2x2 - 14 = 0.
    • Деякі члени можуть дорівнювати 0. Хоча 2x2 - 14 = 0 є найпростішою формою квадратного рівняння, його можна записати у вигляді 2x2 + 0х + (-14) = 0. Це, ймовірно, допоможе на ранній стадії, щоб записати рівняння в стандартній формі квадратного рівняння, навіть якщо деякі члени 0.
  3. Вирішіть рівняння, підставивши числа з квадратного рівняння в формулу для обчислення коренів квадратного рівняння. Формула: x = (- b + / - √(b2 - 4ac))/2a) допоможе знайти значення «х».[6] у цю формулу підставте відповідні числа з рівняння, отриманого в кроці 2.
    • X = (- b + / - √(b2 - 4ac))/2a. у нашому прикладі 2x2 - 14 = 0, a = 2, b = 0, c = -14.
    • X = (-0 +/- √(02 - 4(2)(-14)))/2(2)
    • X = (+/- √( 0 - -112))/2(2)
    • X = (+/- √(112))/2(2)
    • X = (+/- 10,58/4)
    • X =+/- 2,64
  4. Перевірте відповідь, підставивши знайдені значення " х " у вихідне квадратне рівняння.[7] у нашому прикладі підставте 2,64 і -2,64 у вихідне квадратне рівняння.

Поради

  • Перетворення дробів в еквівалентні дроби насправді є їх множенням на 1. При перетворенні 1/2 В 2/4, множення чисельника і знаменника на 2 насправді є множення 1/2 на 2/2, де 2/2=1.
  • Якщо необхідно перевірити еквівалентність змішаних чисел (наприклад, 1 3/4, 2 5/8, 5 2/3 і так далі), то спочатку їх необхідно перетворити в неправильні дроби. Якщо вам потрібно знайти еквівалентну дріб змішаного числа, то це можете зробити двома способами: Перетворіть змішане число в неправильну дріб і скористайтеся методами, описаними в даній статті; або застосуєте методи, описані в даній статті, безпосередньо до змішаного числа.
    • Для перетворення змішаного числа в неправильну дріб помножте цілу частину змішаного числа на знаменник дробової частини, а потім складіть отриманий результат з чисельником дробової частини. Знаменник залиште без змін. Наприклад, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Потім знайдіть еквівалентну дріб: 5/3 x 2/2 = 10/6; отримана дріб еквівалентна змішаному числу 1 2/3.
    • Якщо ви не хочете конвертувати змішане число в неправильну дріб, просто ігноруйте цілу частину змішаного числа і працюйте з його дробовою частиною. Наприклад, в змішаному числі 3 4/16 працюйте тільки з 4/16. 4/16 ÷ 4/4 = 1/4. Потім до отриманого результату припишіть цілу частину вихідного змішаного числа і отримаєте еквівалентну дріб: 3 1/4.

Попередження

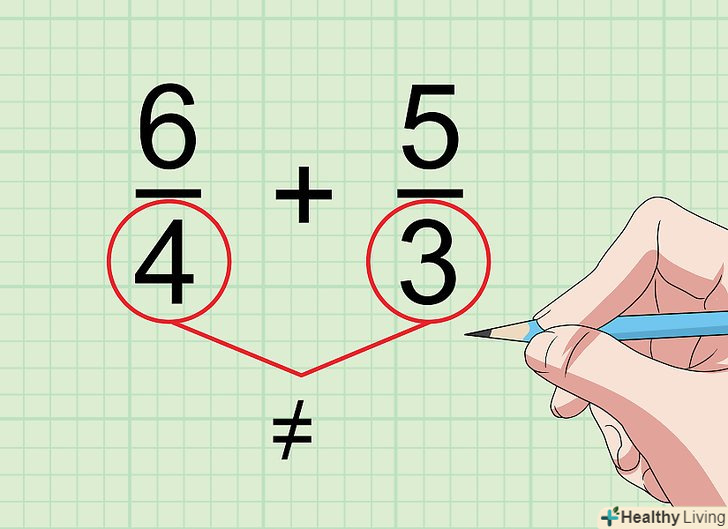
  • Незважаючи на те, що при перемноженні дробів і чисельники, і знаменники відповідно перемножуються, при додаванні і відніманні дробів знаменник залишається колишнім.
    • Наприклад, 4/8 ÷ 4/4 = 1/2 . Але 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 або 3/2, тобто при додаванні Ви отримаєте зовсім інший результат.
  • Для отримання еквівалентних дробів ви множите або ділите чисельник і знаменник на одне і те ж число; це вірно, так як в цьому випадку ви множите або ділите всю дріб на 1 (2/2, 3/3 і так далі), що не змінює значення вихідної дробу. Цього не можна досягти при додаванні або відніманні дробів.

Джерела

  1. ↑ Http://www.themathpage.com/arith/equivalent-fractions.htm
  2. ↑ Http://www.helpwithfractions.com/math-homework-helper/equivalent-fractions/
  3. ↑ Http://www.helpwithfractions.com/math-homework-helper/equivalent-fractions/
  4. ↑ Http://web.mnstate.edu/peil/MDEV102/U3/S22/S22_print.html
  5. ↑ Http://www.purplemath.com/modules/solvquad4.htm
  6. ↑ Http://www.purplemath.com/modules/solvquad4.htm
  7. ↑ Http://www.purplemath.com/modules/solvquad4.htm

Ще почитати: