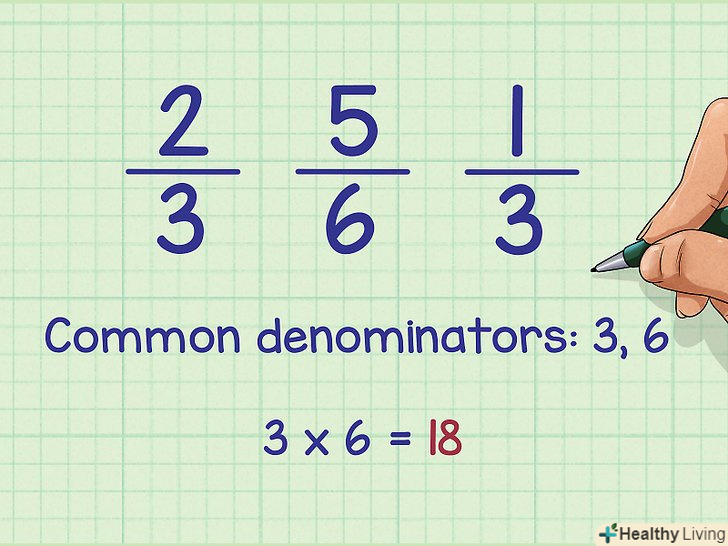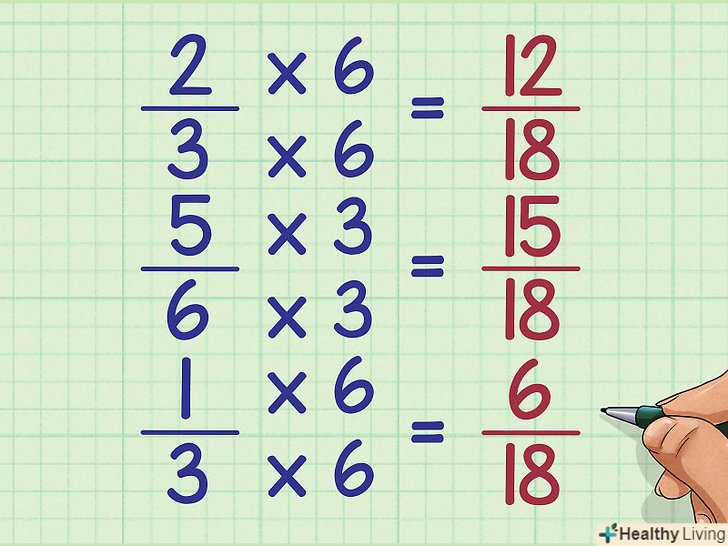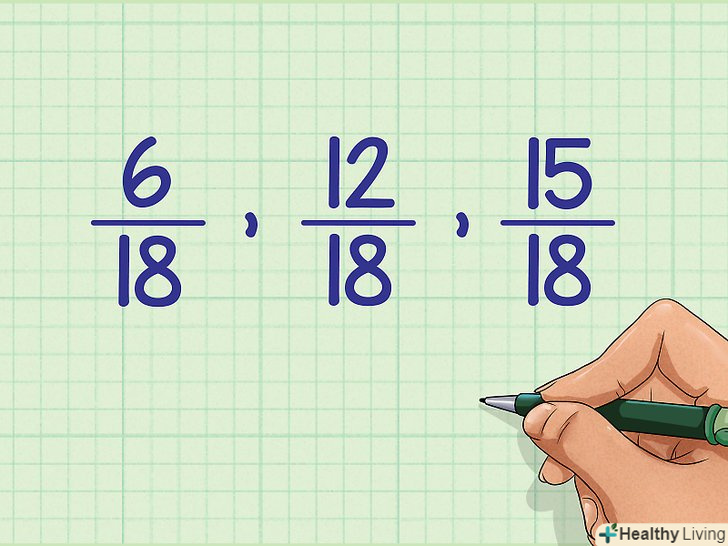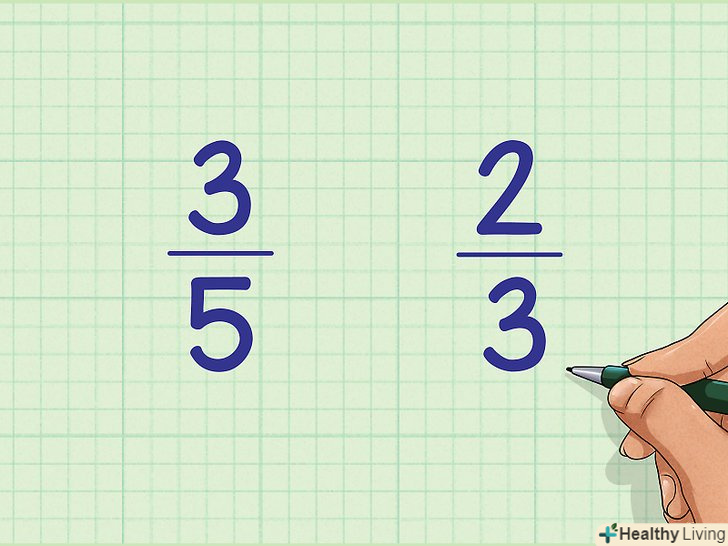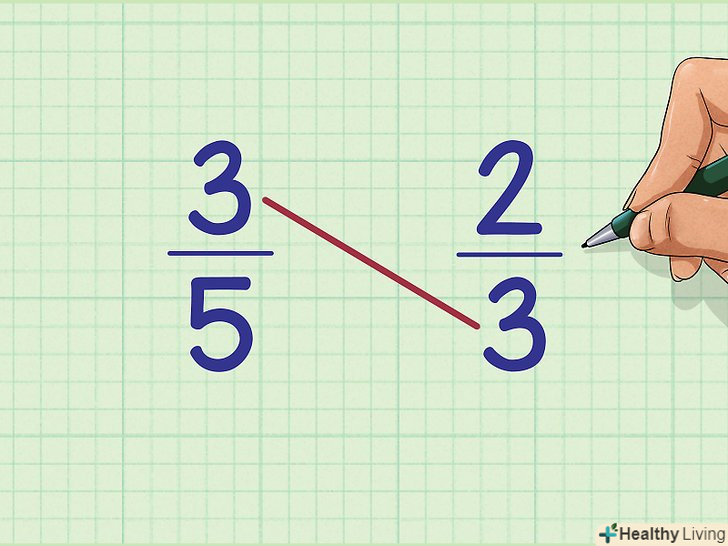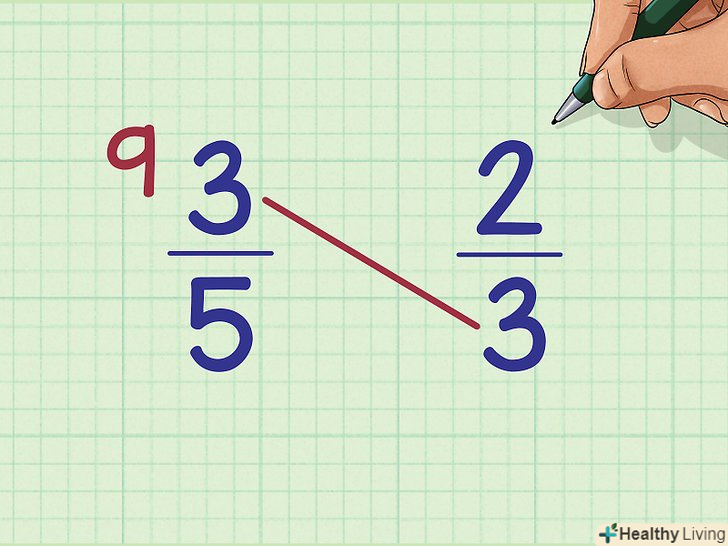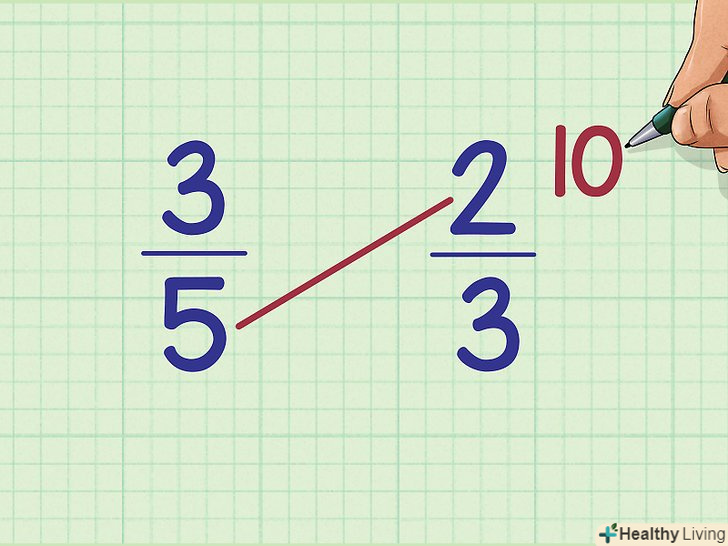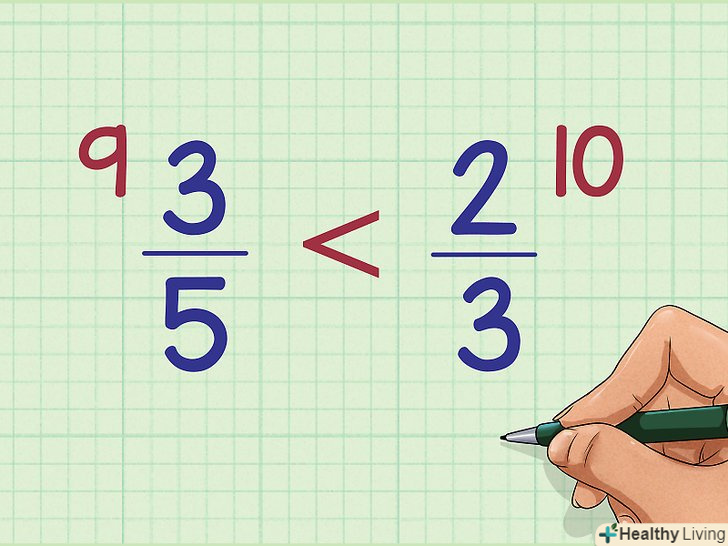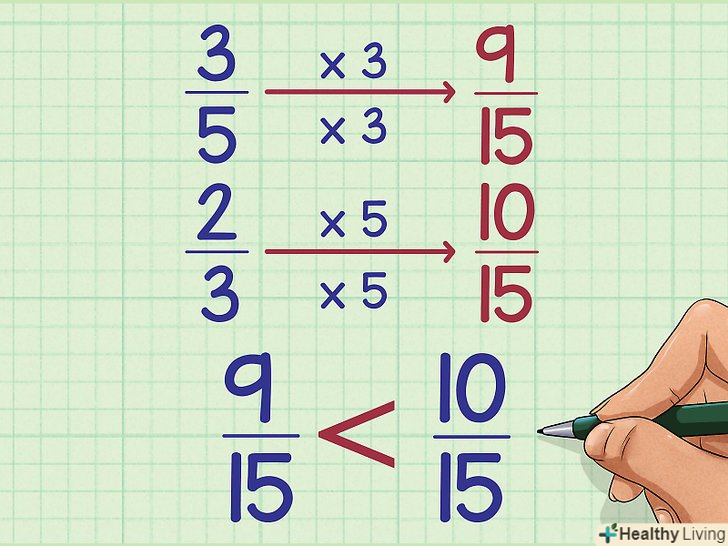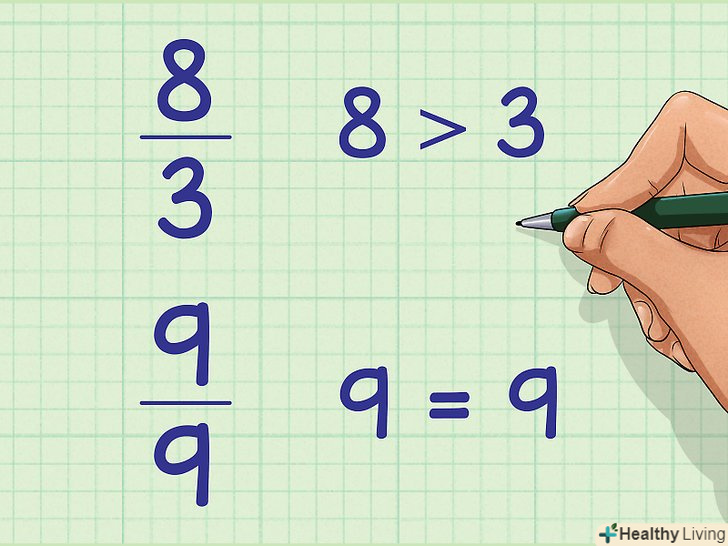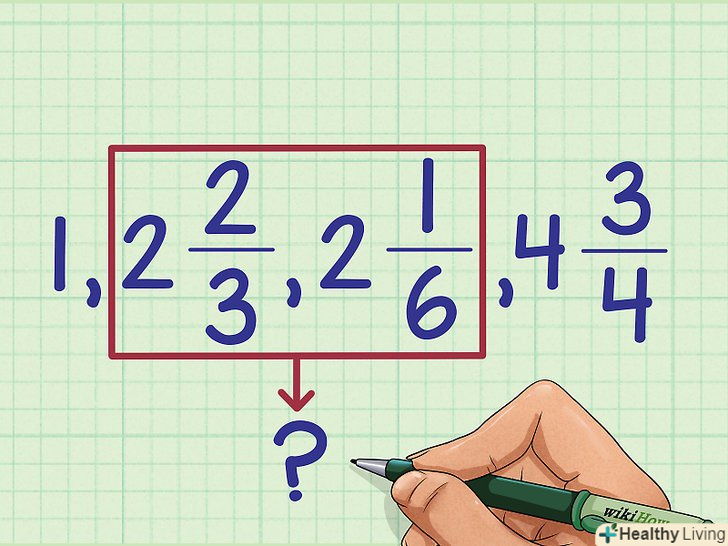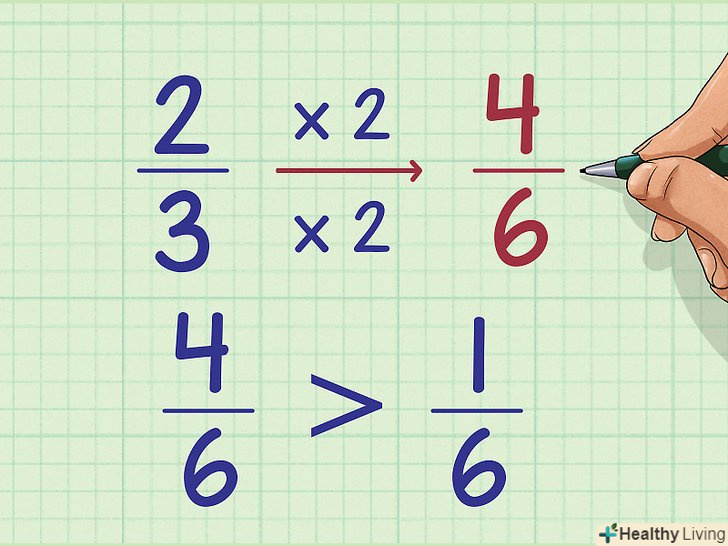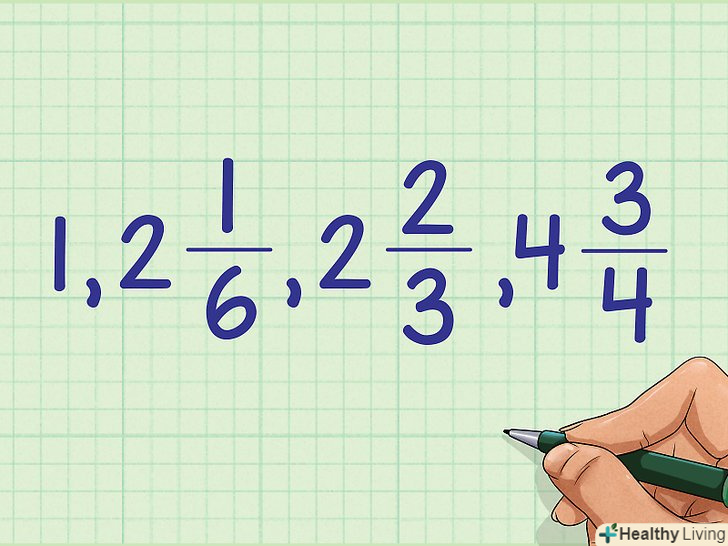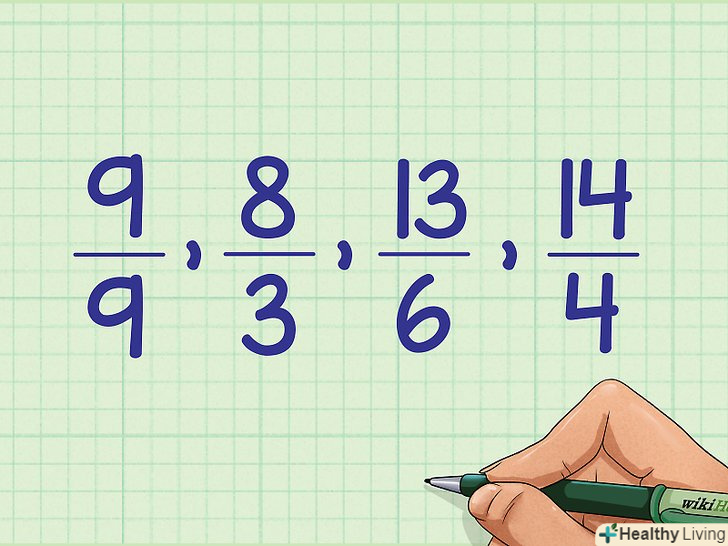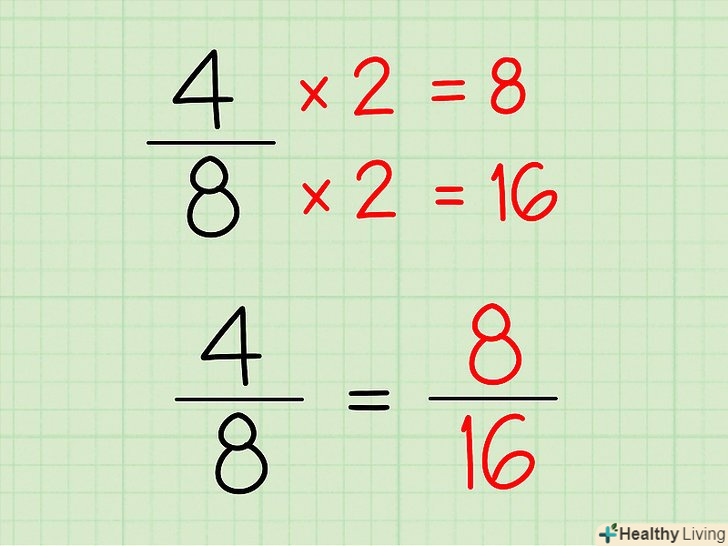1. Головна
    2. Математика
    3. Як упорядкувати дроби за зростанням-

Як упорядкувати дроби за зростанням-

Упорядкування дробів за зростанням (від меншої до більшої) може ввести в оману, так як на відміну від цілих чисел (1, 3, 8) дроби включають чисельник і знаменник. Упорядкувати дроби легко, якщо у них однакові знаменники, наприклад, 1/5, 3/5, 8/5; в іншому випадку необхідно привести всі дроби до спільного знаменника. Ця стаття розповість вам, як упорядкувати дві дроби, будь-яку кількість дробів і неправильні дроби (7/3).

Метод1З 3:
Довільна кількість дробів

  1. ЗнайдітьЗагальний знаменник, що дозволить вам упорядкувати будь-яку кількість дробів. ви можете знайти просто спільний знаменник, або найменший спільний знаменник (НОЗ). Для цього використовуйте один з наступних методів:[1]
    • Перемножте різні знаменники. Наприклад, якщо ви упорядковуєте дроби 2/3, 5/6, 1/3, перемножте два різних знаменника: 3 х 6 = 18. Це простий спосіб, але в більшості випадків ви не знайдете НОЗ.
    • Або напишіть кратні кожного знаменника, а потім виберіть число, що зустрічається у всіх списках кратних. У нашому прикладі кратними 3 є числа: 3, 6, 9, 12, 15, 18; кратними 6 є числа: 6, 12, 18. Так як число 18 зустрічається в обох списках, то це спільний знаменник цих дробів (тут НОЗ = 6, але ми будемо працювати з числом 18).
  2. Приведіть кожен дріб до спільного знаменника. для цього помножте чисельник і знаменник дробу на число, рівне результату ділення спільного знаменника на знаменник конкретного дробу (пам'ятайте, що при множенні чисельника і знаменника на одне число значення дробу не змінюється). У нашому прикладі наведіть дроби 2/3, 5/6, 1/3 до спільного знаменника 18.
    • 18 ÷ 3 = 6, тому 2/3 = (2x6) / (3x6)=12/18
    • 18 ÷ 6 = 3, тому 5/6 = (5x3) / (6x3)=15/18
    • 18 ÷ 3 = 6, тому 1/3 = (1X6) / (3x6)=6/18
  3. Упорядкуйте дроби згідно їх чисельникам (від меншого до більшого).у нашому прикладі правильний порядок буде таким: 6/18, 12/18, 15/18.
  4. Не змінюючи порядок дробів, перепишіть їх у вихідному вигляді.для цього спростіть їх, розділивши чисельник і знаменник на відповідне число.
    • 6/18 = (6 ÷ 6)/(18 ÷ 6) = 1/3
    • 12/18 = (12 ÷ 6)/(18 ÷ 6) = 2/3
    • 15/18 = (15 ÷ 3)/(18 ÷ 3) = 5/6
    • Відповідь: 1/3, 2/3, 5/6

Метод2 З 3:
Два дроби (за допомогою множення хрест-навхрест)

  1. Запишіть два дроби поруч один з одним.наприклад, упорядкуйте дроби 3/5 і 2/3. Зліва напишіть 3/5, а праворуч 2/3.
  2. Помножте чисельник першого дробу на знаменник другого дробу.у нашому прикладі помножте чисельник першого дробу (3) на знаменник другого дробу (3): 3 х 3 = 9.
    • Цей метод називається "множенням хрест-навхрест", тому що ви перемножуєте числа, розташовані по діагоналі.
  3. Напишіть отриманий результат близько першого дробу.у нашому прикладі напишіть 9 близько 3/5 (ліворуч).
  4. Помножте чисельник другого дробу на знаменник першого дробу.у нашому прикладі: 2 х 5 = 10.
  5. Напишіть отриманий результат біля другого дробу.у нашому прикладі напишіть 10 близько 2/3 (праворуч).
  6. Порівняйте два отримані результати.у нашому прикладі 9 менше 10, тому дріб біля 9 (3/5) менше дробу біля 10 (2/3).
    • Результат перемноження завжди пишіть поруч з дробом, а саме над її чисельником.
  7. Пояснення викладеного методу.для впорядкування двох дробів необхідно привести їх до спільного знаменника. Так ось множення хрест-навхрест і призводить два дроби до спільного знаменника![2] тут ми просто не пишемо знаменники, так як вони однакові, а відразу порівнюємо чисельники дробів. Ось наш приклад без множення хрест-навхрест:
    • 3/5=(3x3)/(5x3)=9/15
    • 2/3=(2x5)/(3x5)=10/15
    • Таким чином, 3/5 менше 2/3.

Метод3 З 3:
Неправильні дроби

  1. Неправильна дріб - це дріб, у якій чисельник більше або дорівнює знаменнику, наприклад, 8/3 або 9/9 (тобто значення дробу дорівнює або більше одиниці). [3]
    • Ви можете використовувати інші методи для неправильних дробів. Однак описаний метод є простим і швидким.
  2. Перетворіть кожну неправильну дріб в змішане число.змішане число-вид запису неправильного дробу, що включає цілу і дробову частини. Ви можете це зробити в розумі (наприклад, 9/9 = 1) або за допомогою ділення в стовпчик. Цілий результат ділення записується в цілу частину змішаного числа, а залишок – в чисельник дробової частини (знаменник не змінюється). Наприклад:
    • 8/3 = 2 + 2/3
    • 9/9 = 1
    • 19/4 = 4 + 3/4
    • 13/6 = 2 + 1/6
  3. Для початку упорядкуйте змішані числа по їх цілим частинам (про дробові частини на час забудьте).
    • 1-найменше число.
    • 2 + 2/3 і 2 + 1/6 – тут ми не знаємо, яке з цих змішаних чисел більше.
    • 4 + 3/4 – найбільше змішане число.
  4. Якщо у двох змішаних чисел однакові цілі частини, порівняйте їх дробові частини, привівши останні до спільного знаменника.у нашому прикладі у змішаних чисел 2 + 2/3 і 1/6 + 2 Порівняйте дробові частини:
    • 2/3 = (2x2)/(3x2) = 4/6
    • 1/6 = 1/6
    • 4/6 більше 1/6
    • 2 + 4/6 більше 2 + 1/6
    • 2 + 2/3 більше 2 + 1/6
  5. Упорядкуйте змішані числа за зростанням. у нашому прикладі: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.
  6. Не змінюючи порядку змішаних чисел, перетворіть їх назад в неправильні дроби.у нашому прикладі: 9/9, 8/3, 13/6, 19/4.

Поради

  • Якщо вам дано багато дробів, порівнюйте і упорядковуйте їх, розбивши на невеликі групи (по 2, 3, 4 дробу).
  • Якщо у дробів однакові чисельники, то записуйте їх в порядку, починаючи з більшого знаменника, наприклад, 1/8 &#lt;1/7 &#lt;1/6 &#lt;1/5.
  • Цілком допустимо порівнювати дроби, привівши їх просто до спільного знаменника (тобто шукати найменший спільний знаменник не обов'язково). Спробуйте впорядкувати дроби 2/3, 5/6, 1/3, використовуючи загальний знаменник 36, – Ви отримаєте той же результат.

Джерела

  1. ↑ Http://www.mathsisfun.com/least-common-denominator.html
  2. ↑ Http://www.mathsisfun.com/algebra/cross-multiply.html
  3. ↑ Http://www.mathvillage.info/node/76
  4. Http://www.mathgoodies.com/lessons/fractions/order.html
  5. Http://mathcentral.uregina.ca/QQ/database/QQ.09.06/justin2.html
  6. Http://www.mathvillage.info/node/76

Ще почитати: