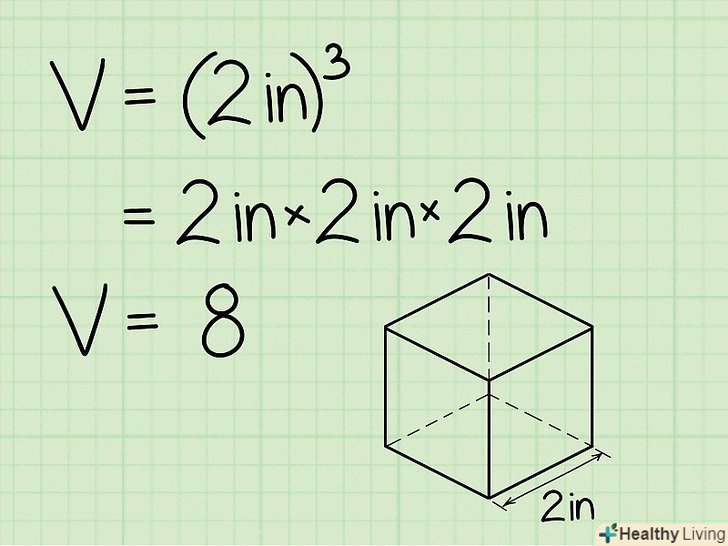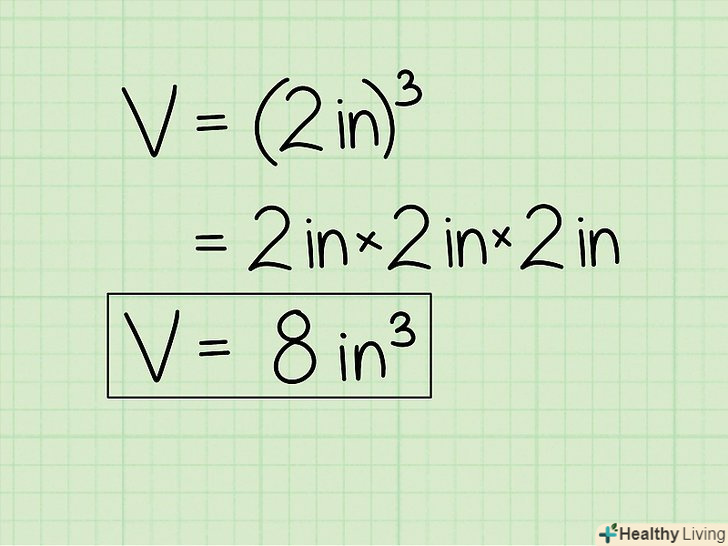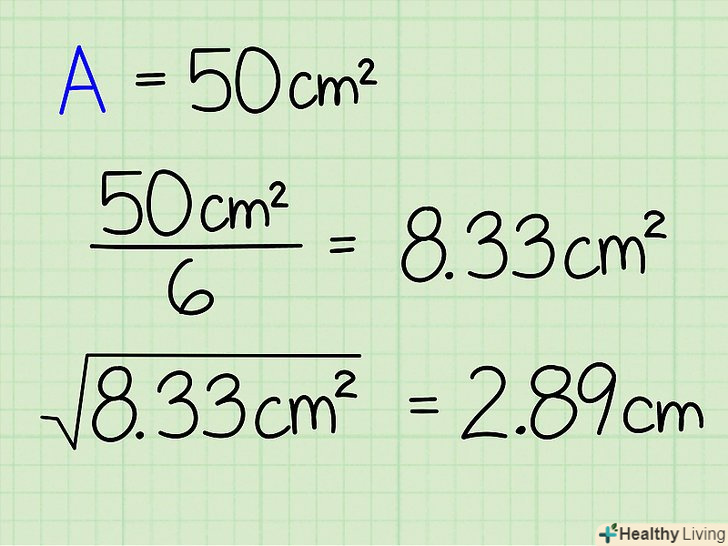1. Головна
    2. Геометрія
    3. Як обчислити об'єм куба

Як обчислити об'єм куба

Куб-тривимірна геометрична фігура, у якій всі ребра рівні (довжина дорівнює ширині і дорівнює висоті). У куба шість квадратних граней, які перетинаються під прямим кутом і сторони яких рівні. Обчислити обсяг куба легко-потрібно перемножити довжину, ширину і висоту. Так як у куба довжина дорівнює ширині і дорівнює висоті, то обсяг куба дорівнюєS3, де s — Довжина одного (будь-якого) ребра куба.

Метод1З 3:
Зведення в куб ребра куба

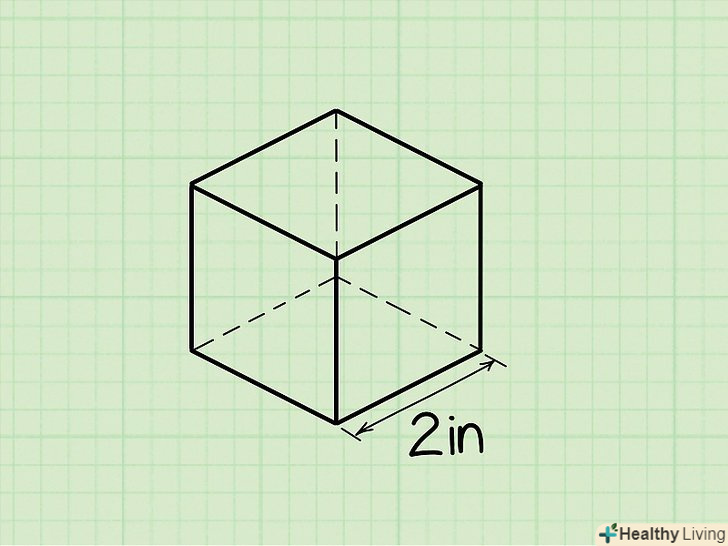
  1. Знайдіть довжину одного ребра куба.як правило, довжина ребра куба дана в умові завдання. Якщо ви обчислюєте обсяг реального об'єкта кубічної форми, виміряйте його ребро лінійкою або рулеткою.
    • Розглянемо приклад. Ребро куба дорівнює 5 см. Знайдіть обсяг куба.
  2. Зведіть в куб довжину ребра куба.іншими словами, помножте довжину ребра куба саму на себе три рази. Якщо S-довжина ребра куба, то s * s * s = s3 і, таким чином, ви обчислите обсяг куба.
    • Цей процес аналогічний процесу знаходження площі підстави куба (дорівнює добутку довжини на ширину квадрата в підставі) і подальшого множення площі підстави на висоту куба (тобто, іншими словами, ви множите довжину на ширину і на висоту). Так як в кубі довжина ребра дорівнює ширині і дорівнює висоті, то цей процес можна замінити зведенням ребра куба в третю ступінь.
    • У нашому прикладі обсяг куба дорівнює 5 * 5 *5 = 53 = 125.
  3. До відповіді припишіть одиниці виміру обсягу (якщо ви цього не зробите, ваша оцінка може бути знижена).Так як обсяг — це кількісна характеристика простору, займаного тілом, то одиницями вимірювання обсягу є кубічні одиниці (кубічні сантиметри, кубічні метри і так далі).
    • У нашому прикладі розмір ребра куба давався в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах (або в см3). Отже, обсяг куба дорівнює 125 см3.
    • Якщо розмір ребра куба дається в інших одиницях, то і обсяг куба вимірюється у відповідних кубічних одиницях. Наприклад, якщо ребро куба дорівнює 5 м (а не 5 см), то його обсяг дорівнює 125 м3.

Метод2 З 3:
Обчислення об'єму за площею поверхні

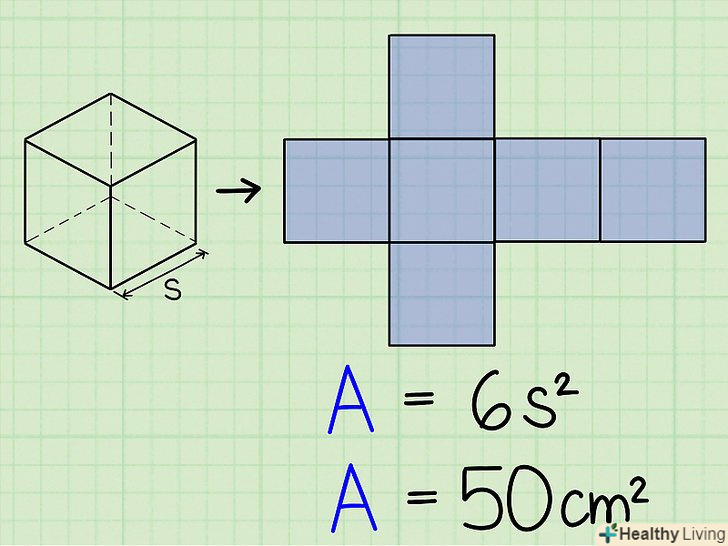
  1. У деяких завданнях довжина ребра куба не дана, але дані інші величини, за допомогою яких можна знайти ребро куба і його обсяг.наприклад, якщо вам дана площа поверхні куба, то розділіть її на 6, з отриманого значення витягніть квадратний корінь і ви знайдете довжину ребра куба. Потім зведіть довжину ребра куба в третю ступінь і обчисліть обсяг куба.
    • Площа поверхні куба дорівнює6s2, де s-довжина ребра куба (тобто ви знаходите площу однієї грані куба, а потім множите її на 6, так як у куба 6 рівних граней).
    • Розглянемо приклад. Площа поверхні куба дорівнює50 см2. Знайдіть обсяг куба.
  2. Розділіть площу поверхні куба на 6 (так як у куба 6 рівних граней, Ви отримаєте площу однієї грані куба).у свою чергу площа однієї грані куба дорівнює s2, де s — довжина ребра куба.
    • У нашому прикладі: 50/6 =8,33 см2 (не забувайте, що площа вимірюється в квадратних одиницях — см2, м2 і так далі).
  3. Так як площа однієї грані куба дорівнює s2, то витягніть квадратний корінь із значення площі однієї грані і отримаєте довжину ребра куба.
    • У нашому прикладі, √8,33 =2,89 см.
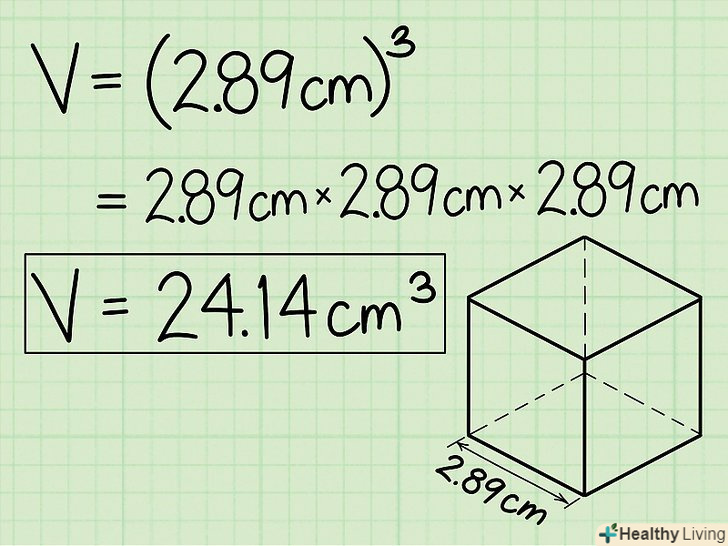
  4. Зведіть в куб отримане значення, щоб знайти обсяг куба (як описано в попередньому розділі).
    • У нашому прикладі: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см3. До відповіді не забудьте приписати кубічні одиниці.

Метод3 З 3:
Обчислення об'єму по діагоналі

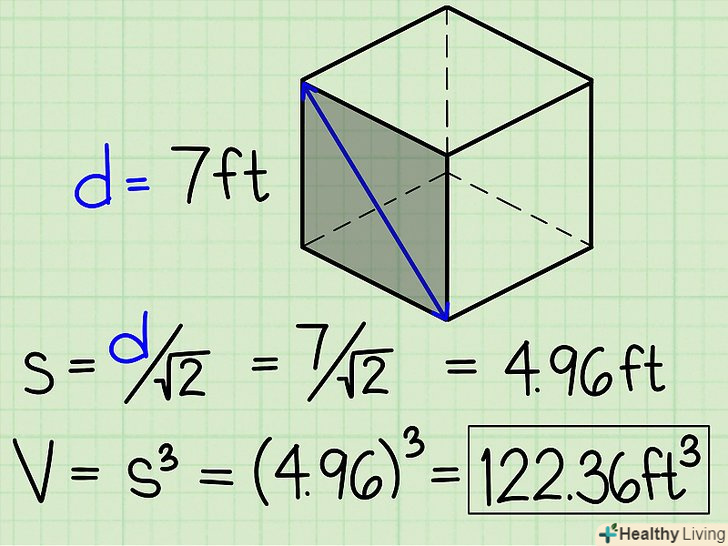
  1. Розділіть діагональ однієї з граней куба на √2, щоб знайти довжину ребра куба.таким чином, якщо в задачі дана діагональ грані (будь-який) куба, то ви можете знайти довжину ребра куба, розділивши діагональ на √2.
    • Розглянемо приклад. Діагональ грані куба дорівнює 7 см. Знайдіть обсяг куба. У цьому випадку довжина ребра куба дорівнює 7 / √2 = 4,96 см.Об'єм куба дорівнює 4,963 = 122,36 см3.
    • Запам'ятайте: d2 = 2s2, де d — діагональ грані куба, s — ребро куба. Ця формула випливає з теореми Піфагора, згідно з якою квадрат гіпотенузи (в нашому випадку діагональ грані куба) прямокутного трикутника дорівнює сумі квадратів катетів (в нашому випадку ребер), тобто d2 = s2 + s2 = 2s2.
  2. Розділіть діагональ куба на √3, щоб знайти довжину ребра куба.таким чином, якщо в задачі дана діагональ куба, то ви можете знайти довжину ребра куба, розділивши діагональ на √3. Діагональ куба-відрізок, що з'єднує дві вершини, симетричні щодо центру куба, рівний D2 = 3S2 (де D — діагональ куба, s — ребро куба).
    • Ця формула випливає з теореми Піфагора, згідно з якою квадрат гіпотенузи (в нашому випадку діагональ куба) прямокутного трикутника дорівнює сумі квадратів катетів (в нашому випадку один катет — це ребро, а другий катет — це діагональ грані куба, рівна 2s2), тобто D2 = s2 + 2s2 = 3s>2.
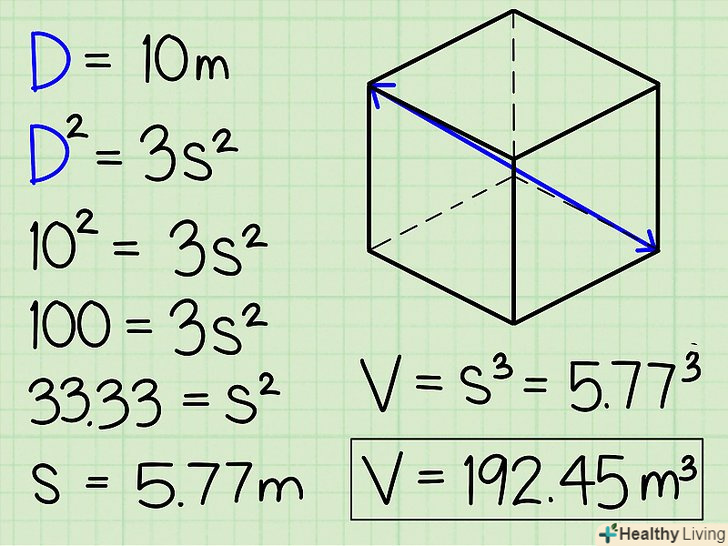
    • Розглянемо приклад. Діагональ куба дорівнює 10 м. знайдемо обсяг куба:
      • D2 = 3s2
      • 102 = 3s2
      • 100 = 3s2
      • 33,33 = s2
      • 5,77 м = s
      • Об'єм куба дорівнює 5,773 = 192,45 м3

Ще почитати: