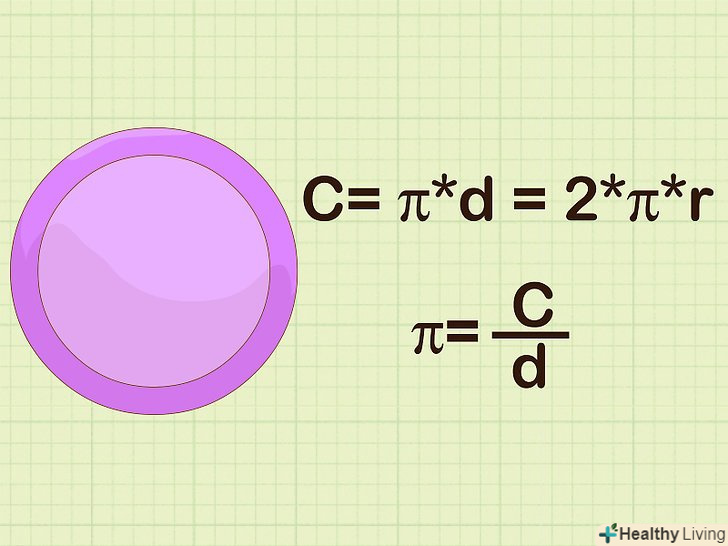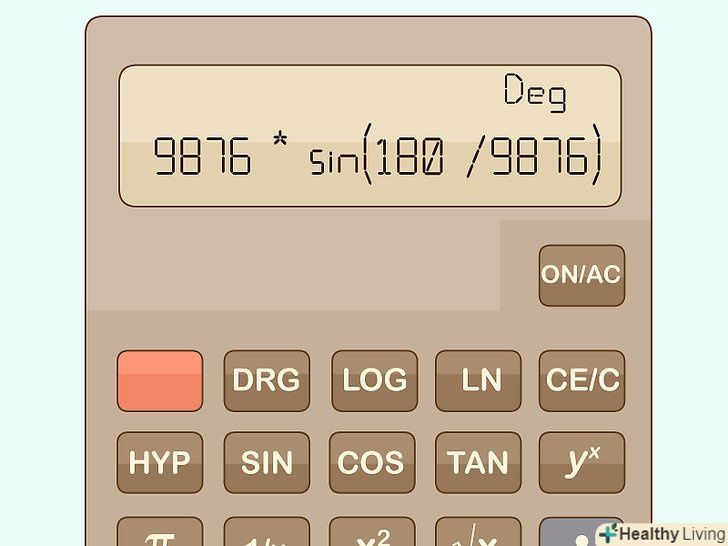Пі — π) - одне з найважливіших і інтригуючих чисел в математиці. Ця константа, приблизно рівна 3,14, використовується для обчислення довжини кола з урахуванням її радіуса.[1] це також ірраціональне число, тобто воно може бути обчислено до нескінченного числа знаків після коми.[2] це не так-то просто зробити, але все-таки можливо.
Кроки
Метод1З 5:
Обчислення Пі через вимірювання окружності
Метод1З 5:
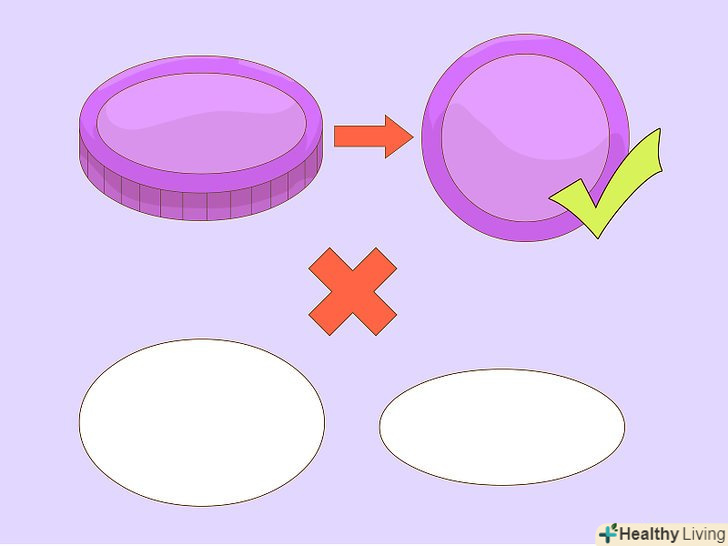
 Переконайтеся, що ви використовуєте ідеальне коло. цей метод не працює з еліпсами, овалами і чим-небудь іншим, цей метод підходить тільки для ідеальної окружності. Окружність визначається як сукупність всіх точок на площині, які лежать на однаковій відстані від однієї центральної точки. Кришка банки-ідеальний предмет для цього методу. Якщо ви хочете зробити найбільш точні обчислення, використовуйте олівець з дуже тонким грифелем.
Переконайтеся, що ви використовуєте ідеальне коло. цей метод не працює з еліпсами, овалами і чим-небудь іншим, цей метод підходить тільки для ідеальної окружності. Окружність визначається як сукупність всіх точок на площині, які лежать на однаковій відстані від однієї центральної точки. Кришка банки-ідеальний предмет для цього методу. Якщо ви хочете зробити найбільш точні обчислення, використовуйте олівець з дуже тонким грифелем. Виміряйте довжину кола настільки точно, наскільки це можливо.це нелегке завдання (ось чому Пі так важливо).
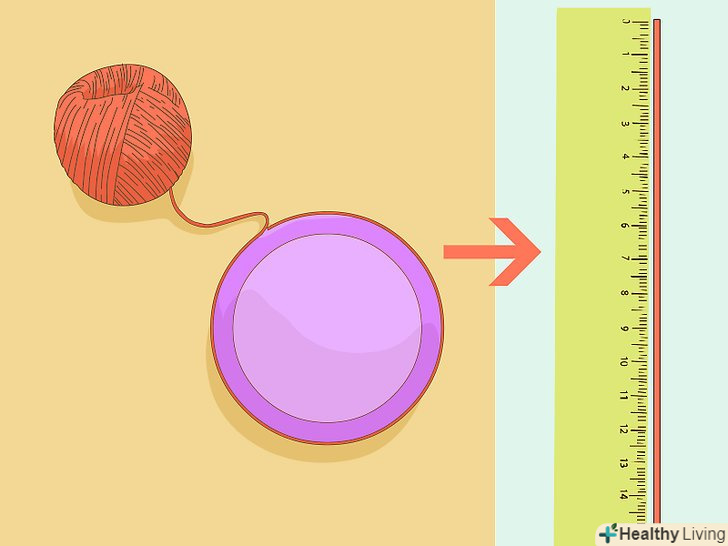
Виміряйте довжину кола настільки точно, наскільки це можливо.це нелегке завдання (ось чому Пі так важливо).- Оберніть нитку навколо кришки якомога щільніше. Відзначте точку збігу початку і кінця, а потім виміряйте довжину нитки за допомогою лінійки.
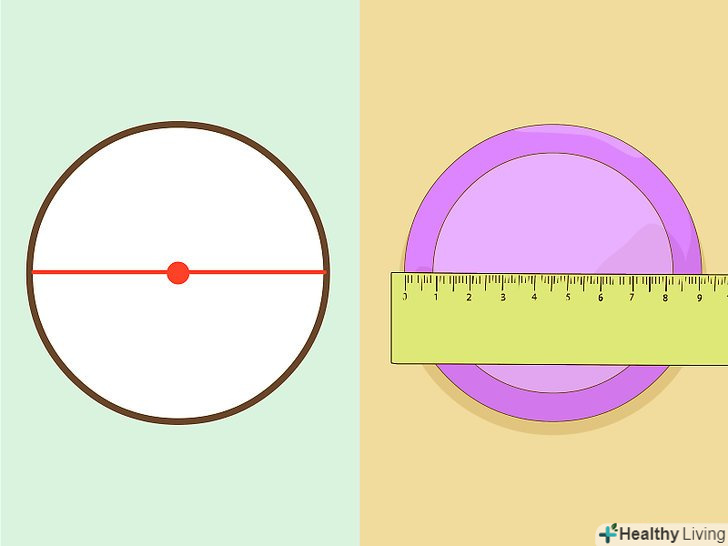
 Виміряйте діаметр кола.діаметр - довжина відрізка, що проходить через центр кола і будь-які дві точки, що лежать на окружності.
Виміряйте діаметр кола.діаметр - довжина відрізка, що проходить через центр кола і будь-які дві точки, що лежать на окружності. Використовуйте формулу.довжина кола обчислюється за формулою C= π*d = 2*π*r. Таким чином, Пі дорівнює довжині кола, поділеної на її діаметр. Порахуйте Пі (з вашими значеннями) на калькуляторі. Результат повинен бути приблизно дорівнює 3,14.[3]
Використовуйте формулу.довжина кола обчислюється за формулою C= π*d = 2*π*r. Таким чином, Пі дорівнює довжині кола, поділеної на її діаметр. Порахуйте Пі (з вашими значеннями) на калькуляторі. Результат повинен бути приблизно дорівнює 3,14.[3] Щоб уточнити розрахунки, повторіть цю процедуру з декількома різними колами, а потім усередніть результати.ваші вимірювання не будуть досконалими для однієї взятої окружності, але з урахуванням декількох кіл, вони повинні усереднитися до точного значення Пі.
Щоб уточнити розрахунки, повторіть цю процедуру з декількома різними колами, а потім усередніть результати.ваші вимірювання не будуть досконалими для однієї взятої окружності, але з урахуванням декількох кіл, вони повинні усереднитися до точного значення Пі.
Метод2З 5:
Обчислення Пі за допомогою нескінченного числового ряду
Метод2З 5:
 Використовуйте ряд Лейбніца. Математики знайшли кілька різних нескінченних рядів, які дозволяють точно обчислити Пі до великої кількості знаків після коми. Деякі з них настільки складні, що потрібні суперкомп'ютери для обробки. Однак одним з найпростіших рядів є ряд Лейбніца. Хоча він і не найефективніший, з кожною ітерацією він буде давати більш точне значення Пі; після 500 000 ітерацій ряд Лейбніца дасть точне значення Пі з десятьма знаками після коми.[4] Here is the formula to apply.
Використовуйте ряд Лейбніца. Математики знайшли кілька різних нескінченних рядів, які дозволяють точно обчислити Пі до великої кількості знаків після коми. Деякі з них настільки складні, що потрібні суперкомп'ютери для обробки. Однак одним з найпростіших рядів є ряд Лейбніца. Хоча він і не найефективніший, з кожною ітерацією він буде давати більш точне значення Пі; після 500 000 ітерацій ряд Лейбніца дасть точне значення Пі з десятьма знаками після коми.[4] Here is the formula to apply.- Π = (4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...
- Візьміть 4/1 і відніміть 4/3. Потім додайте 4/5. Потім відніміть 4/7. Продовжуйте, чергуючи додавання і віднімання дробів з 4 в чисельнику і кожним наступним непарним числом в знаменнику. Чим більше разів ви це зробите, тим більш точне значення Пі Ви отримаєте.
 Спробуйте ряд Нілаканта.це ще один нескінченний ряд для обчислення Пі, який досить легко зрозуміти. Цей ряд більш складний, ніж ряд Лейбніца, але він дає точне значення Пі набагато швидше.[5]
Спробуйте ряд Нілаканта.це ще один нескінченний ряд для обчислення Пі, який досить легко зрозуміти. Цей ряд більш складний, ніж ряд Лейбніца, але він дає точне значення Пі набагато швидше.[5]- Π = 3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11*12) - (4/(12*13*14) ...
- Для цього ряду запишіть число 3 і чергуйте додавання і віднімання дробів з числом 4 в чисельнику і добутком трьох послідовних цілих чисел, які збільшуються з кожною новою ітерацією, в знаменнику. Кожен наступний твір починається з найбільшого числа, використовуваного в попередньому творі. Виконайте це всього кілька разів і ви отримаєте досить точне значення Пі.
Метод3З 5:
Обчислення Пі методом голки Буффона
Метод3З 5:
 ПроведітьЕксперимент . виявляється, Пі можна знайти, провівши цікавий експеримент під назвою метод голки Буффона, [6] який прагне визначити ймовірність того, що випадково кинуті голки Приземляться або між намальованими рівновіддаленими паралельними прямими, або перетнуть рівно одну пряму. Якщо відстань між прямими дорівнює довжині голки, то відношення числа кидків, коли голка перетинає пряму, до загального числа кидків прагне до 2/Пі. Також можете спробувати провести експеримент з хот-догами (перейдіть за посиланням на початку кроку).
ПроведітьЕксперимент . виявляється, Пі можна знайти, провівши цікавий експеримент під назвою метод голки Буффона, [6] який прагне визначити ймовірність того, що випадково кинуті голки Приземляться або між намальованими рівновіддаленими паралельними прямими, або перетнуть рівно одну пряму. Якщо відстань між прямими дорівнює довжині голки, то відношення числа кидків, коли голка перетинає пряму, до загального числа кидків прагне до 2/Пі. Також можете спробувати провести експеримент з хот-догами (перейдіть за посиланням на початку кроку).- Вчені і математики не можуть визначити точний спосіб обчислення Пі, так як вони не можуть знайти настільки тонкий предмет, щоб обчислення були точними.[7]
- Вчені і математики не можуть визначити точний спосіб обчислення Пі, так як вони не можуть знайти настільки тонкий предмет, щоб обчислення були точними.[7]
Метод4З 5:
Обчислення Пі з використанням межі
Метод4З 5:
 Спочатку виберіть велике число.чим більше це число, тим точніше буде результат.
Спочатку виберіть велике число.чим більше це число, тим точніше буде результат. Потім підставте це число(позначимо його х) в формулу для розрахунку Пі: x * sin (180 / x)'. Щоб цей метод спрацював, калькулятор потрібно включити в режимі»градуси". Ми говоримо, що в цьому методі використовується межа, так як результат обмежений числом Пі (тобто значення Пі є гранично можливим). Чим більше значення х, тим точніше ви розрахуєте Пі.
Потім підставте це число(позначимо його х) в формулу для розрахунку Пі: x * sin (180 / x)'. Щоб цей метод спрацював, калькулятор потрібно включити в режимі»градуси". Ми говоримо, що в цьому методі використовується межа, так як результат обмежений числом Пі (тобто значення Пі є гранично можливим). Чим більше значення х, тим точніше ви розрахуєте Пі.
Метод5З 5:
Функція арксинус
Метод5З 5:
 Виберіть будь-яке число від -1 до 1. Функція y=arcsin (x) не має таких значень x, великих 1 і менших -1, яким можна було б зіставити хоч яке-небудь значення y (неважливо — нескінченне чи ні). Це означає, що функція y=arcsin (x) визначена тільки на інтервалі від x=-1 до x=1 включно і не визначена при будь-яких інших x.
Виберіть будь-яке число від -1 до 1. Функція y=arcsin (x) не має таких значень x, великих 1 і менших -1, яким можна було б зіставити хоч яке-небудь значення y (неважливо — нескінченне чи ні). Це означає, що функція y=arcsin (x) визначена тільки на інтервалі від x=-1 до x=1 включно і не визначена при будь-яких інших x. Підставте своє число в наступну формулу і ви зможете обчислити число Пі.
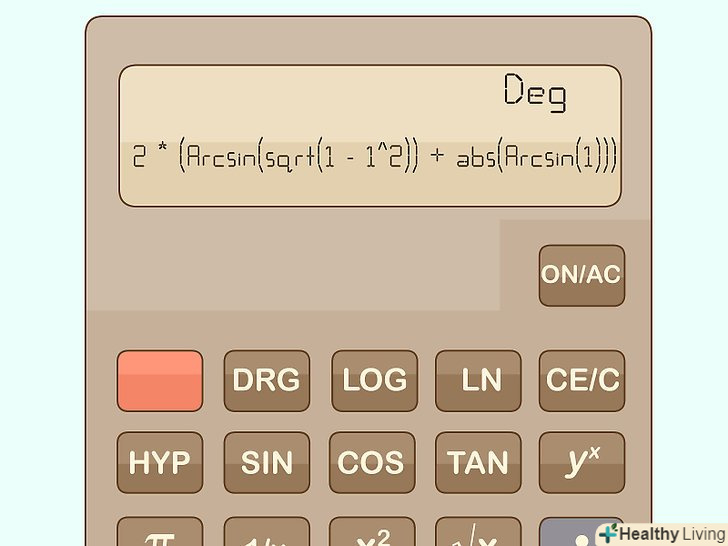
Підставте своє число в наступну формулу і ви зможете обчислити число Пі.- Пі = 2 * (Arcsin (SQRT (1 - х ^ 2))) + ABS (Arcsin (х)).
- Значення арксинуса буде представлено в радіанах.
- Sqrt-це квадратний корінь.
- Abs-це абсолютне значення числа
- Х ^ 2-в даному випадку це х в квадраті.
- Пі = 2 * (Arcsin (SQRT (1 - х ^ 2))) + ABS (Arcsin (х)).
Поради
- Розрахунок Пі-захоплююче і цікаве заняття, але обчислення багатьох знаків після коми не має великого сенсу. Астрофізики стверджують, що значення Пі з 39 знаками після коми достатньо для космологічних розрахунків, які проводяться з точністю до розмірів атома.
Джерела
- ↑ Https://www.mathsisfun.com/definitions/pi.html
- ↑ Http://mathworld.wolfram.com/IrrationalNumber.html
- ↑ Http://www.mathsisfun.com/numbers/pi.html
- ↑ Http://en.wikipedia.org/wiki/Pi
- ↑ Http://www.mathscareers.org.uk/article/calculating-pi/
- ↑ https://mste.illinois.edu/activity/buffon/
- ↑ Http://mathworld.wolfram.com/BuffonsNeedleProblem.html