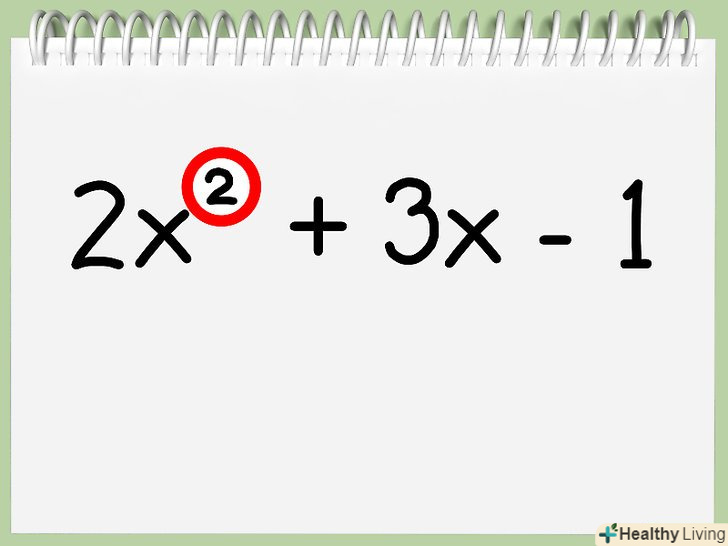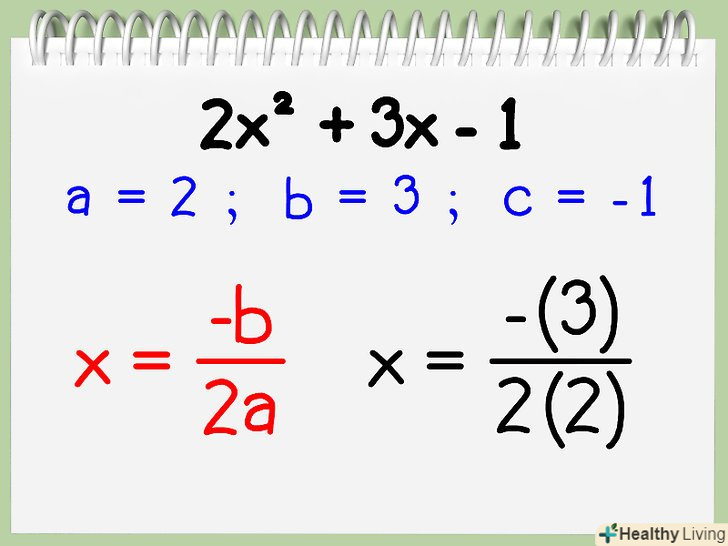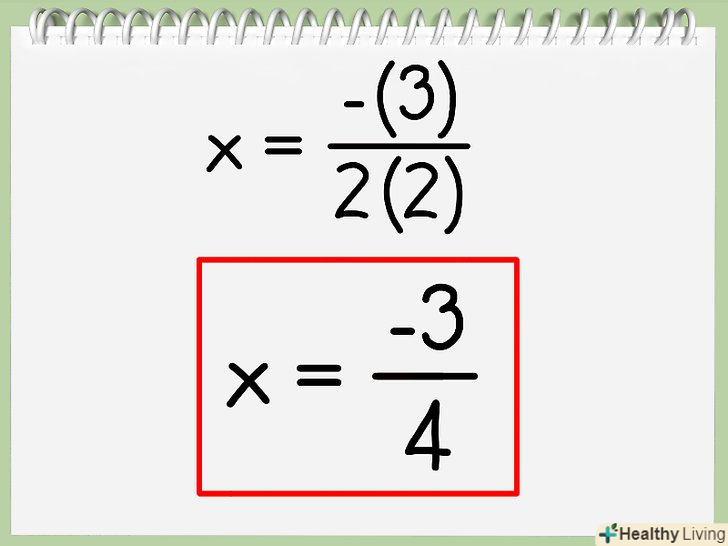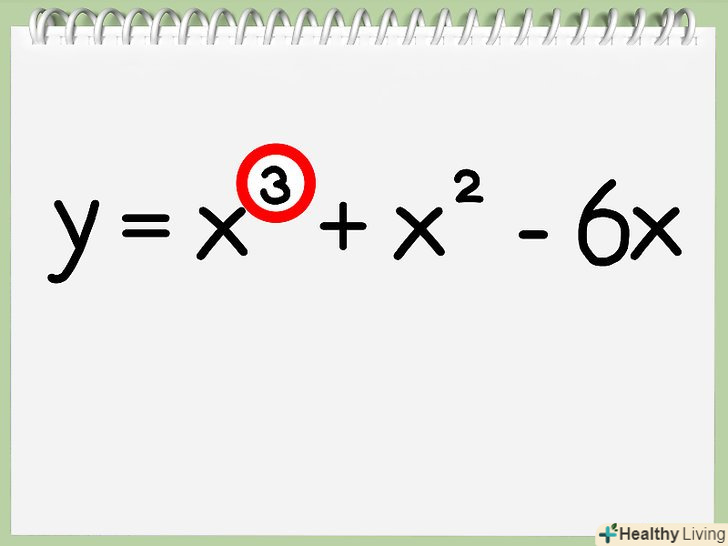Багато характеристик графіка функції або многочлена неможливо пояснити без візуального представлення. Одна з таких характеристик-вісь симетрії: вертикальна лінія на графіку, яка ділить цей графік на два дзеркально симетричних зображення. Знайти вісь симетрії для даного многочлена відносно нескладно.[1] існує два основних способи.
Кроки
Метод1 З 2:
Знаходження осі симетрії для квадратного тричлена
Метод1 З 2:
 Визначте, який ступінь многочлена.ступінь многочлена-це найбільша ступінь, яку мають одночлени в цьому вираженні.[2] якщо ступінь даного многочлена дорівнює 2 (жоден одночлен у виразі не має ступеня вище, ніж x2), ви можете знайти вісь симетрії, використовуючи даний спосіб. Якщо ступінь многочлена більше двох, застосовуйте другий спосіб.
Визначте, який ступінь многочлена.ступінь многочлена-це найбільша ступінь, яку мають одночлени в цьому вираженні.[2] якщо ступінь даного многочлена дорівнює 2 (жоден одночлен у виразі не має ступеня вище, ніж x2), ви можете знайти вісь симетрії, використовуючи даний спосіб. Якщо ступінь многочлена більше двох, застосовуйте другий спосіб.- Щоб наочно продемонструвати цей спосіб, візьмемо, наприклад, многочлен виду 2x2 + 3x – 1. Найвища ступінь в многочлені-x2, отже, ми маємо справу з квадратним тричленом і можемо скористатися першим способом для знаходження осі симетрії.
 Підставте коефіцієнти в формулу розрахунку осі симетрії. для знаходження осі симетрії для квадратного тричлена виду ax2 + bx +c (парабола), застосовують базову формулу x = -b/2A.[3]
Підставте коефіцієнти в формулу розрахунку осі симетрії. для знаходження осі симетрії для квадратного тричлена виду ax2 + bx +c (парабола), застосовують базову формулу x = -b/2A.[3]- У нашому прикладі a = 2, b = 3, and c = -1. Підставимо ці значення в нашу формулу, і отримуємо:
x = -3 / 2(2) = -3/4.
- У нашому прикладі a = 2, b = 3, and c = -1. Підставимо ці значення в нашу формулу, і отримуємо:
 Запишіть рівняння осі симетрії. значення, яке ви розрахували за формулою осі симетрії, - це значення точки перетину осі симетрії з віссю абсцис.
Запишіть рівняння осі симетрії. значення, яке ви розрахували за формулою осі симетрії, - це значення точки перетину осі симетрії з віссю абсцис.- У наведеному вище прикладі вісь симетрії дорівнює -3 / 4.
Метод2 З 2:
Знаходження осі симетрії графічним способом
Метод2 З 2:
 Визначте ступінь многочлена.ступінь многочлена-це найбільша ступінь, яку мають одночлени в цьому вираженні. Якщо ступінь даного многочлена дорівнює 2 (жоден одночлен у виразі не має ступеня вище, ніж x2), ви можете знайти вісь симетрії, використовуючи вищенаведений спосіб. Якщо ступінь многочлена більше 2, застосовуйте графічний спосіб.
Визначте ступінь многочлена.ступінь многочлена-це найбільша ступінь, яку мають одночлени в цьому вираженні. Якщо ступінь даного многочлена дорівнює 2 (жоден одночлен у виразі не має ступеня вище, ніж x2), ви можете знайти вісь симетрії, використовуючи вищенаведений спосіб. Якщо ступінь многочлена більше 2, застосовуйте графічний спосіб. Накресліть систему координат. намалюйте дві лінії, що перетинаються під прямим кутом у вигляді знака "плюс". Горизонтальна лінія буде віссю x, а вертикальна — віссю у.
Накресліть систему координат. намалюйте дві лінії, що перетинаються під прямим кутом у вигляді знака "плюс". Горизонтальна лінія буде віссю x, а вертикальна — віссю у. Відкладіть одиничні Числові відрізки на осях.відкладіть на осях Числові відрізки рівної величини.
Відкладіть одиничні Числові відрізки на осях.відкладіть на осях Числові відрізки рівної величини. Розрахуйте значення y = f(x) для кожного значення x.Візьміть даний многочлен або функцію і розрахуйте значення f (x), послідовно підставивши в вираз значення x.
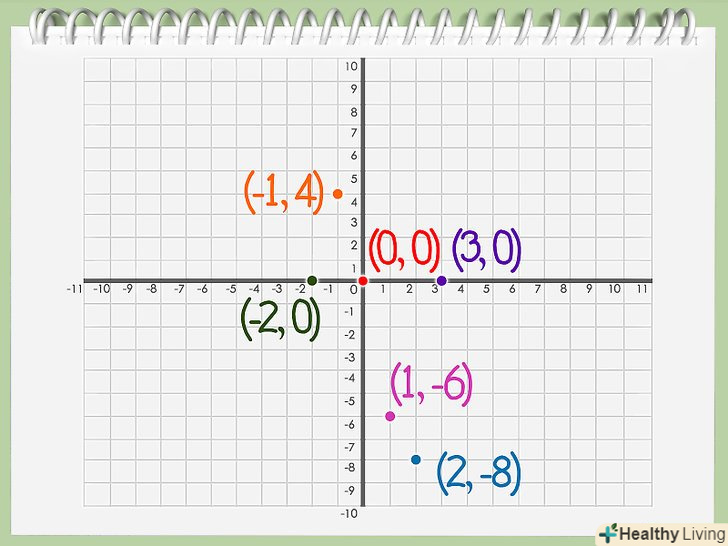
Розрахуйте значення y = f(x) для кожного значення x.Візьміть даний многочлен або функцію і розрахуйте значення f (x), послідовно підставивши в вираз значення x. Позначте точки на графіку для кожної пари координат. Тепер у вас є відповідне значення y = f(x) для кожного значення на осі абсцис. Для кожної точки з координатами (x, y), відзначте точку в системі координат - по вертикалі відклавши значення по осі X, а по горизонталі — на осі Y.
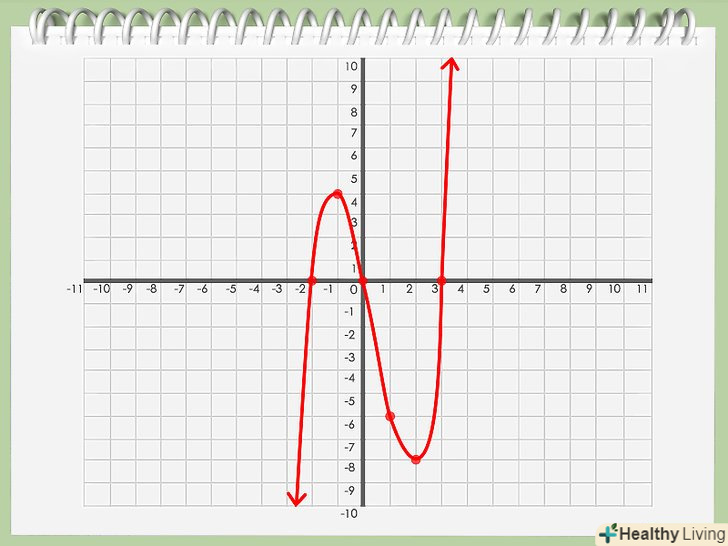
Позначте точки на графіку для кожної пари координат. Тепер у вас є відповідне значення y = f(x) для кожного значення на осі абсцис. Для кожної точки з координатами (x, y), відзначте точку в системі координат - по вертикалі відклавши значення по осі X, а по горизонталі — на осі Y. Намалюйте графік многочлена.коли ви нанесли всі точки на систему координат, можна плавно з'єднати їх між собою. У вас вийде безперервний графік вашого многочлена.
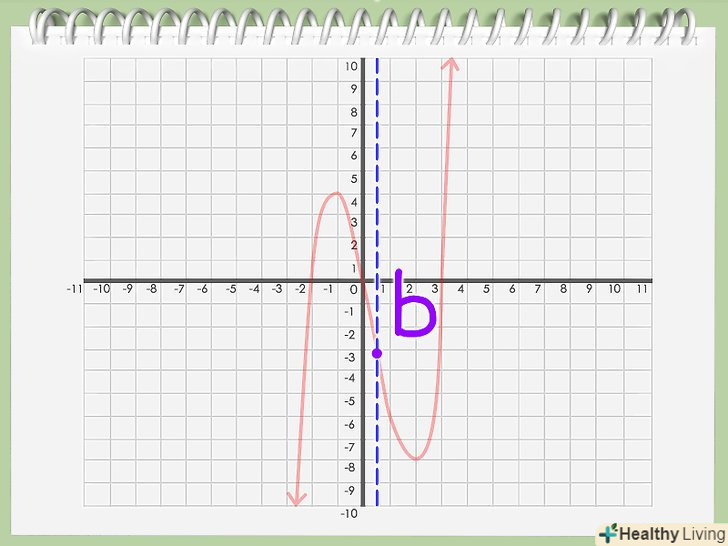
Намалюйте графік многочлена.коли ви нанесли всі точки на систему координат, можна плавно з'єднати їх між собою. У вас вийде безперервний графік вашого многочлена. Знайдіть вісь симетрії. Уважно вивчіть отриманий графік. Знайдіть точку на графіку, по якій можна провести лінію, що розділяє графік на дві рівні дзеркальні половини.[4]
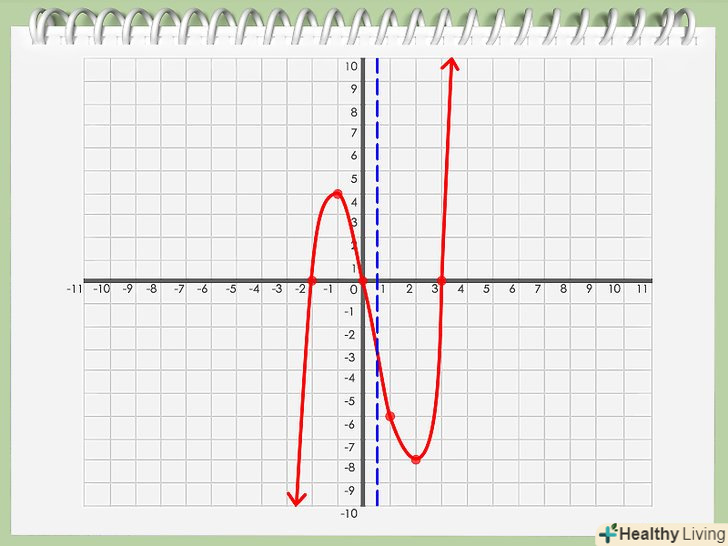
Знайдіть вісь симетрії. Уважно вивчіть отриманий графік. Знайдіть точку на графіку, по якій можна провести лінію, що розділяє графік на дві рівні дзеркальні половини.[4] Позначте вісь симетрії. якщо ви знайшли таку точку (назвемо її "b") на осі x, яка розділяє графік на дві дзеркальні половини, це значення і буде шуканої віссю симетрії.
Позначте вісь симетрії. якщо ви знайшли таку точку (назвемо її "b") на осі x, яка розділяє графік на дві дзеркальні половини, це значення і буде шуканої віссю симетрії.
Поради
- Довжина осей абсцис і ординат повинна бути достатньою, щоб наочно відобразити форму графіка.
- Деякі многочлени не мають осі симетрії. Наприклад, для y = 3x не існує осі симетрії.
- Симетрія многочлена може бути визначена як парна або непарна. Будь-який графік, вісь симетрії якого збігається з віссю У має "парну" симетрію. Будь-який графік, вісь симетрії якого збігається з віссю x — « "непарний".
Джерела
- Http://www.basic-mathematics.com/degree-of-a-polynomial.html
- Http://www.virtualnerd.com/algebra-1/quadratic-equations-functions/graphing/graph-basics/axis-symmetry-example
- ↑ Https://www.purplemath.com/modules/symmetry3.htm
- ↑ https://www.mathsisfun.com/algebra/degree-expression.html
- ↑ Https://www.mathplanet.com/education/algebra-1/quadratic-equations/the-graph-of-y-ax-2-plus-bx-plus-c
- ↑ Https://www.khanacademy.org/math/algebra2/polynomial-functions/introduction-to-symmetry-of-functions/v/recognizing-odd-and-even-functions