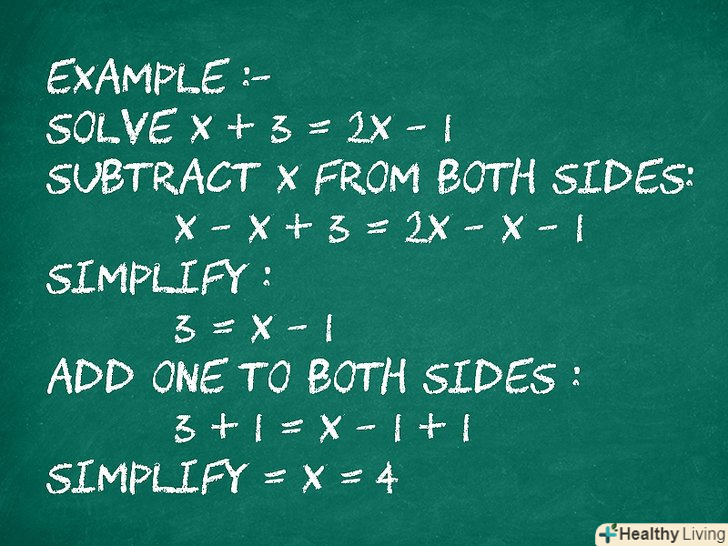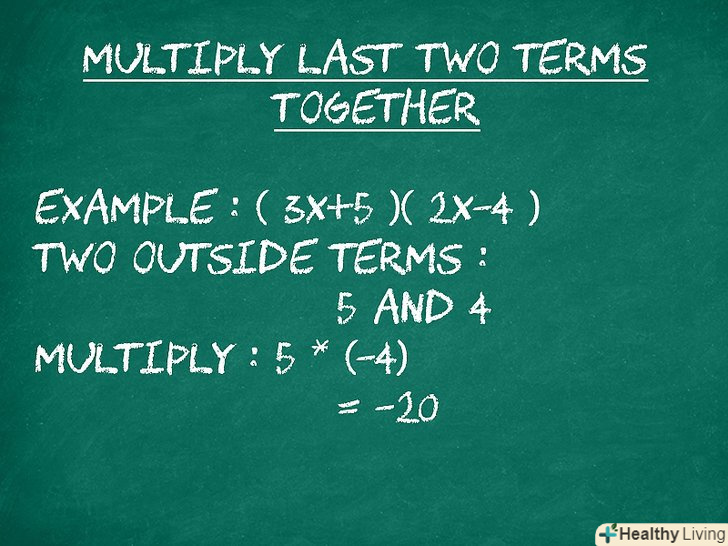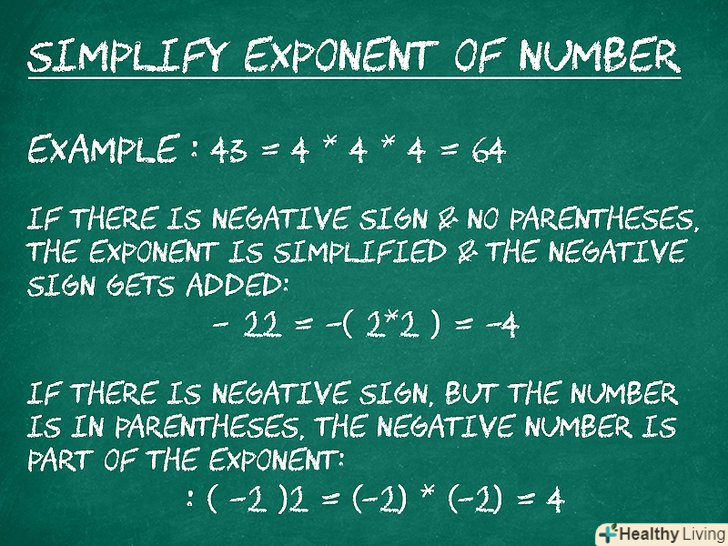1. Головна
    2. Математика
    3. Як почати розбиратися в алгебрі (з ілюстраціями)

Як почати розбиратися в алгебрі (з ілюстраціями)

Деяким учням алгебра дається з працею. Крім чисел в алгебраїчних рівняннях присутні букви, які представляють собою невідомі значення. На перший погляд це досить складно, але якщо розібратися з деякими основними концепціями і попрактикуватися у вирішенні завдань, можна з легкістю впоратися з алгеброю. Вивчивши основи, ви зрозумієте, наскільки алгебра корисна, в тому числі в повсякденному житті!

Частина1З 4:
Правильний порядок операцій

  1. Запам'ятайте правильний порядок виконання математичних операцій.Порядок такий: дужки, ступінь, множення і ділення, додавання і віднімання. Вирішуючи будь-яке завдання, почніть з виразу в дужках, потім перейдіть до наступної операції (згідно з наведеним порядком) і закінчите відніманням.[1]
    • Порядок виконання операцій над виразом у дужках такий самий, як наведений вище.
    • Множення і ділення вважаються рівнозначними операціями, які можна виконати одночасно. Тому просто виконуйте операції зліва направо.
    • Додавання і віднімання також є рівнозначними операціями, тому виконуйте їх зліва направо.
    • Ще раз про порядок: дужки, ступінь, множення і ділення, додавання і віднімання.
  2. Використовуйте порядок виконання операцій для вирішення завдань.будь-яку алгебраїчну задачу потрібно вирішувати з використанням правильного порядку виконання математичних операцій. У багатьох завданнях присутні дужки, з яких потрібно починати рішення. Множення і ділення вважаються рівнозначними операціями, тому виконуйте їх зліва направо; це ж стосується додавання і віднімання.[2]
    • Наприклад: обчисліть (3 + 6) х 7 - 4/2.
    • Дужки: 9 х 7 - 4/2
    • Ступінь: немає
    • Множення: 63 - 4/2
    • Поділ: 63 - 2
    • Додавання: немає
    • Віднімання: 61
    • Остаточна відповідь: (3 + 6) х 7 - 4/2 = 61.
  3. Практикуйтеся у вирішенні завдань. [3] чим більше завдань ви вирішите, тим швидше освоїте навички їх вирішення. Зрештою, ви будете автоматично виконувати операції в правильному порядку. Вирішіть таку кількість завдань, яке дозволить вам відчувати себе впевнено в їх вирішенні.
    • Приклад 1: 8 + (6 x 42 + 7) = 8 + (6 x 16 + 7) = 8 + (96 +7) = 8 + 103 = 111.
    • Приклад 2: 30/2 + 52 - (6 x 3) = 30/2 + 52 - 18 = 30/2 + 25 – 18 = 15 + 25 – 18 = 40 – 18 = 22.
  4. Попросіть про допомогу.якщо ви почали вивчати алгебру зовсім недавно, матеріал може здатися надто складним. Тому не соромтеся задавати викладачеві питання або знайдіть інше джерело інформації. Або просто позаймайтеся з друзями, які краще знають алгебру.
    • Якщо ви думаєте, що зовсім не справляєтеся з алгеброю, попросіть батьків найняти репетитора.

Частина2З 4:
Рішення задач

  1. Пам'ятайте, що рішення алгебраїчних задач подібне до складання мозаїки.будь-яке завдання складається з окремих елементів, схожих на шматочки мозаїки. Щоб спростити рішення задачі, навчитеся визначати цифри, змінні і їх позиції.
    • Знайдіть невідоме число в задачі, в якій дано остаточну відповідь.
    • Наприклад: 1 + _ _ = 9
    • Невідоме число-це число 8, так як 1 плюс 8 дорівнює 9. Досить просто, чи не так? Це основи алгебри.[4]
  2. Виконайте операції з обох сторін рівняння.при вирішенні алгебраїчної задачі потрібно пам'ятати, що якщо виконати будь-яку операцію з одного боку рівняння, ту ж операцію потрібно виконати з іншого боку рівняння. Тобто якщо з одного боку рівняння щось додати або відняти або на щось помножити або розділити, ту ж операцію необхідно виконати з іншого боку рівняння.
    • Наприклад: обчисліть х + 3 = 2х -1.
    • Відніміть " х " з обох сторін: х - х + 3 = 2х - х - 1.
    • : 3 = х-1.
    • Додайте 1 до обох сторін: 3 + 1 = х - 1 + 1.
    • Спростіть: х = 4.
  3. Відокремте змінну на одній стороні рівняння.у багатьох алгебраїчних виразах присутні постійні і змінні. Постійна-це число, а змінна – це буква, яка представляє собою невідоме значення.[5]
    • Щоб відокремити змінну, з обох сторін рівняння виконайте певні дії: відніміть або додайте деяке число, а якщо при змінній знаходиться коефіцієнт, розділіть на нього обидві сторони рівняння.
    • Наприклад: 6y + 6 = 48
    • Відніміть 6 з обох сторін: 6y + 6 - 6 = 48 - 6
    • Спростіть: 6y = 42
    • Розділіть обидві частини на 6: 6y / 6 = 42/6
    • Спростіть: у = 7
  4. Витягніть корінь, щоб позбутися від показника ступеня (і навпаки).якщо змінна зводиться в квадрат, потрібно витягти квадратний корінь, щоб вирішити задачу. Якщо змінна стоїть під знаком квадратного кореня, потрібно звести в квадрат, щоб вирішити задачу.[6]
    • Приклад 1: √x = 9
    • Зведіть в квадрат обидві сторони рівняння: √x2 = 92
    • Х = 81
    • Приклад 2: x2 = 16
    • Витягніть квадратний корінь з обох сторін рівняння: √x2 = √16
    • Х = 4
  5. Приведіть подібні члени. якщо в задачі присутні подібні (з однією змінною) члени, можна привести їх, щоб спростити завдання. Це полегшить вирішення завдання. Пам'ятайте, що члени, показники ступенів яких Різні, не є подібними. Наприклад, член " х " не подібний члену x2.[7]
    • Подібні члени: 4x,- 3x, 0,45 x, - 132x
    • Члени, які не є подібними: 5x, 8y2 , -13Y, 9z, 12xy
    • Наприклад, вираз 4x + 3Y-7x містить два подібних члена: 4x і-7x. наведіть їх, щоб отримати спрощений вираз: -3x + 3Y.
  6. Попрактикуйтесь у вирішенні більш складних завдань.практика - це основа оволодіння будь-яким навиком. У міру вирішення завдань беріться за більш складні вирази, щоб по-справжньому освоїти процес. Вирішуйте завдання з підручника або знайдіть їх в Інтернеті.
    • Приклад 1: q + 18 = 9q-6
    • Додайте 6 до обох сторін: q + 18 + 6 = 9q-6 + 6
    • Спростіть: q + 24 = 9q
    • Відніміть q з обох сторін: q - q + 24 = 9q-q
    • Спростіть: 24 = 8q
    • Розділіть обидві сторони на 8: 8q / 8 = 24/8
    • Рішення: q = 3
  7. Перевірте відповідь. Заведіть звичку перевіряти остаточні відповіді. Після того як знайдете рішення, тобто обчисліть значення змінної, перевірте відповідь; для цього підставте його в вихідне рівняння. Якщо рівність дотримується, рішення правильне.
    • Приклад: q = 3 у рівнянні q + 18 = 9q-6
    • 3 + 18 = (9 х 3) - 6
    • 21 = (27) - 6
    • 21 = 21
    • Рівність дотримується, тому відповідь q = 3 вірний.

Частина3З 4:
Перемноження двох біномів

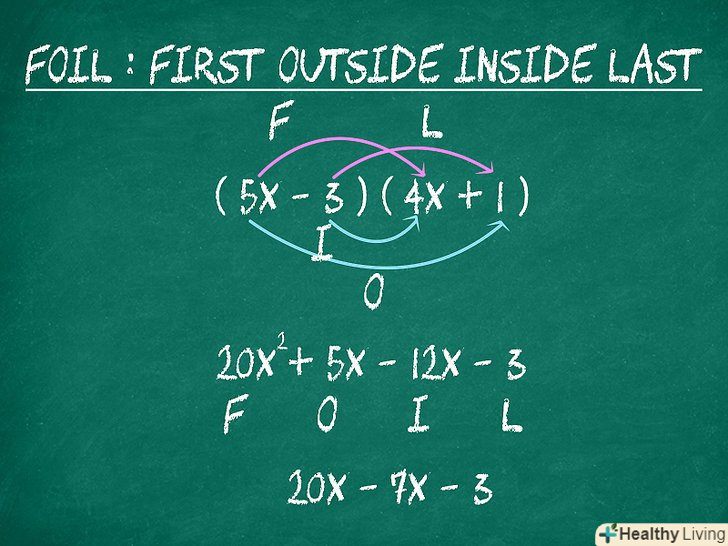
  1. Зрозумійте порядок перемноження членів біномів.цей метод застосовується при перемноженні двох біномів. Біном - це алгебраїчний вираз, який включає два члени, а добуток двох біномів має вигляд: (3x + 5)(2х - 4). Порядок перемноження членів: перші члени, перший і другий члени, другий і перший члени, другі члени.[8]
    • Перші члени-це члени, які в кожній парі дужок стоять першими. У нашому прикладі це 3x і 2x.
    • Перший і другий члени-це перший член у першій парі дужок і другий член у другій парі дужок. У нашому прикладі це 3x і -4.
    • Другий і перший члени-це другий член у першій парі дужок і перший член у другій парі дужок. У нашому прикладі це 5 і 2х.
    • Другі члени-це члени, які в кожній парі дужок стоять другими. У нашому прикладі це 5 і -4.
    • Спростіть отриманий вираз, а потім пишіть остаточну відповідь.
  2. Перемножте перші члени. Визначте перші члени кожного бінома. Перший член-це перший доданок в парі дужок. У нашому прикладі (3x + 5) (2х - 4) першими членами є 3x і 2x. перемножте ці члени.[9]
    • Наприклад: (3x + 5)(2x - 4)
    • Перші члени: 3x і 2x
    • Множення: 3x * 2х = 6x2
  3. Перемножте перший і другий члени. Визначте перший і другий члени. Тут перший член-це перший член у першій парі дужок, а другий член – це другий член у другій парі дужок. У нашому прикладі (3x + 5) (2x - 4) першим і другим членами є 3x і -4. Перемножте ці члени.[10]
    • Наприклад: (3x + 5)(2x - 4)
    • Перший і другий члени: 3X і -4
    • Множення: 3x * (-4) = - 12x
  4. Перемножте другий і перший члени. визначте другий і перший члени. Тут другий член-це другий член у першій парі дужок, а перший член – це перший член у другій парі дужок. У нашому прикладі (3x + 5) (2x-4) другим і першим членами є 5 і 2х. перемножте ці члени.[11]
    • Наприклад: (3x + 5)(2x - 4)
    • Другий і перший члени: 5 і 2x
    • Множення: 5 * 2x = 10x
  5. Перемножте другі члени. Визначте другі члени кожного бінома. Другий член-це другий доданок в парі дужок. У нашому прикладі (3x + 5) (2х - 4) другими членами є 5 і -4. Перемножте ці члени.[12]
    • Наприклад: (3x + 5)(2x - 4)
    • Другі члени: 5 і -4
    • Множення: 5 * (-4) = -20
  6. Складіть знайдені значення і спростіть отриманий вираз.перемноживши відповідні члени, складіть їх (з урахуванням знака кожного члена), а потім приведіть подібні члени, щоб спростити вираз.[13]
    • Наприклад: (3x + 5)(2x - 4)
    • Запишіть вираз: 6x2 - 12x + 10x-20
    • Приведіть подібні члени: 6x2 - 2x - 20

Частина4З 4:
Робота зі ступенями

  1. Спростіть постійну з показником ступеня.якщо число зводиться в деяку ступінь, помножте це число на себе кількість разів, яке дорівнює показнику ступеня. Так спрощується член, який є постійною з показником ступеня.[14]
    • Наприклад: 43 = 4 * 4 * 4 = 64.
    • Якщо перед числом стоїть знак "мінус", а саме число не укладено в дужки, зведіть число в ступінь, а потім до отриманого результату припишіть знак "мінус": -22 = -(2 * 2) = -4.[15]
    • Якщо перед числом стоїть знак "мінус" , а число і знак укладені в дужки, знак "мінус" є частиною підстави ступеня: (-2)2 = -2 * -2 = 4.[16]
  2. Наведіть подібні члени з однаковими показниками ступеня.спочатку досить складно знайти змінну з показником ступеня. Просто запам'ятайте: члени з однією і тією ж змінною і з одним і тим же показником ступеня можна складати і віднімати. Якщо змінні однакові, а показники різні, такі члени складати і віднімати не можна.
    • Приклад 1: 6x2 + 5x2 = 11x2
    • Приклад 2: 4XY3 - 8xy 3 = - 4xy3
    • Приклад 3: 5Z + 5Z2 ; тут немає подібних членів.
  3. Складіть показники ступеня однакових змінних, коли множите їх. якщо однакові змінні перемножуються, і кожна змінна має показник ступеня, складіть показники ступеня, щоб отримати кінцевий показник ступеня. Це стосується лише тих самих змінних.[17]
    • Приклад 1: x2x3 = x 2+3 = x5
    • Приклад 2: (a3b5c2)(ab2) = a3+1b5+2c2 = a4b7c2sup >
  4. Відніміть показники ступеня однакових змінних, коли ділите їх.якщо показник ступеня негативний, це означає, що потрібно виконати операцію ділення: x-1 = 1 / x. Якщо потрібно розділити однакові змінні, і кожна змінна має показник ступеня, відніміть показник ступеня змінної, яка знаходиться в знаменнику (знизу), з показника ступеня змінної, яка знаходиться в чисельнику (зверху).[18]
    • Приклад 1: A6/a 3 = a6-3 = a3
    • Приклад 2: (x4y2 ) / (x6 y2) = x4-6y2-2 = x-2 = 1 / x2

Джерела

  1. ↑ Https://www.mathsisfun.com/operation-order-pemdas.html
  2. ↑ Https://www.mathsisfun.com/operation-order-pemdas.html
  3. ↑ Https://www.mathsisfun.com/operation-order-pemdas.html
  4. ↑ Http://www.mathsisfun.com/algebra/introduction.html
  5. ↑ Http://www.mathsisfun.com/algebra/definitions.html
  6. ↑ Http://www.sosmath.com/algebra/solve/solve2/s21/s21.html
  7. ↑ Http://www.algebrahelp.com/lessons/simplifying/combiningliketerms/
  8. ↑ Http://www.algebrahelp.com/lessons/simplifying/foilmethod/pg2.htm
  9. ↑ Http://www.algebrahelp.com/lessons/simplifying/foilmethod/pg2.htm
  1. ↑ Http://www.algebrahelp.com/lessons/simplifying/foilmethod/pg2.htm
  2. ↑ Http://www.algebrahelp.com/lessons/simplifying/foilmethod/pg2.htm
  3. ↑ Http://www.algebrahelp.com/lessons/simplifying/foilmethod/pg2.htm
  4. ↑ Http://www.algebrahelp.com/lessons/simplifying/foilmethod/pg2.htm
  5. ↑ Http://www.algebrahelp.com/lessons/simplifying/numberexp/index.htm
  6. ↑ Http://www.algebrahelp.com/lessons/simplifying/numberexp/pg2.htm
  7. ↑ Http://www.algebrahelp.com/lessons/simplifying/numberexp/pg3.htm
  8. ↑ Https://www.mathsisfun.com/algebra/variables-exponents-multiply.html
  9. ↑ Https://www.mathsisfun.com/algebra/variables-exponents-multiply.html

Ще почитати: