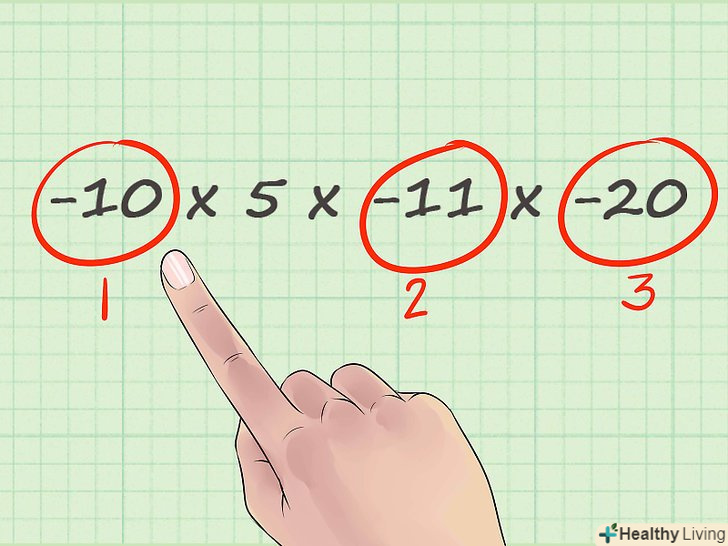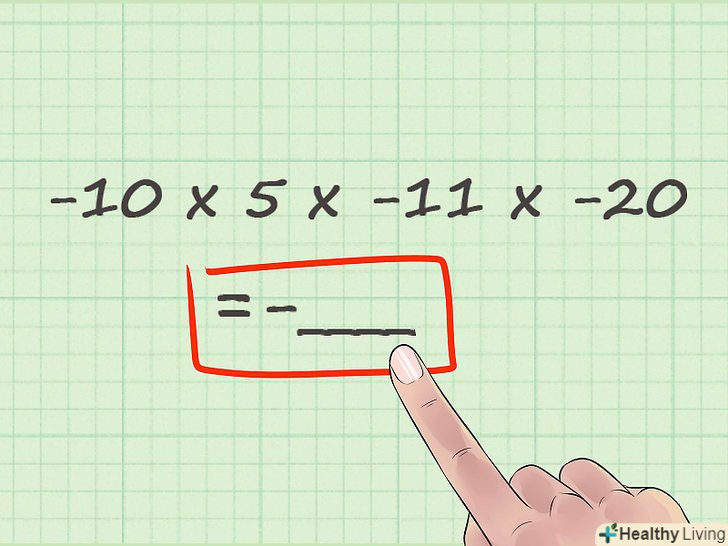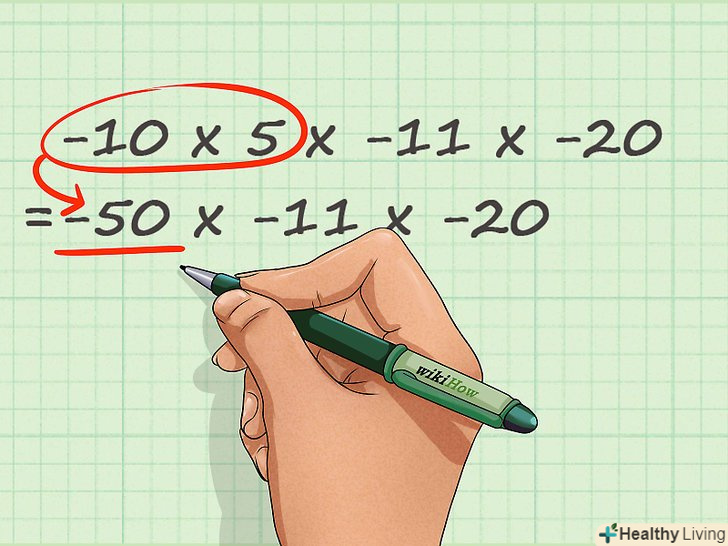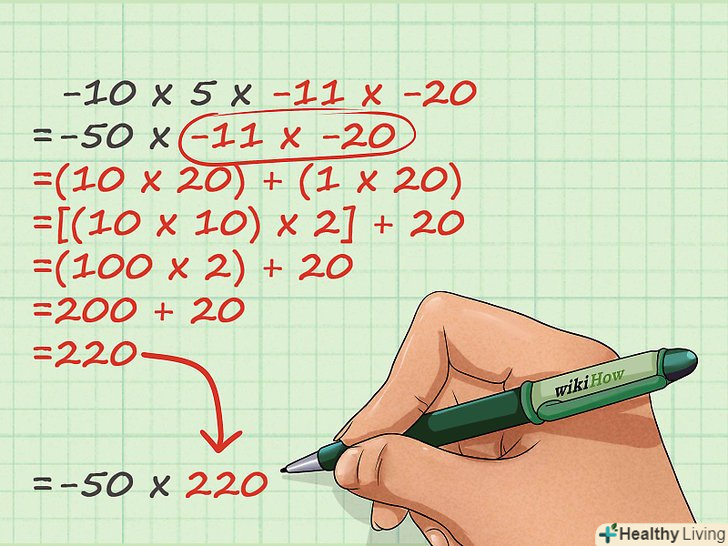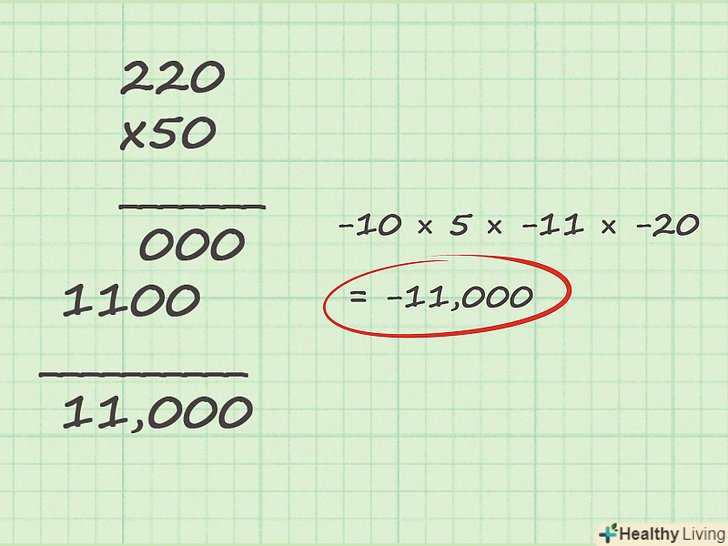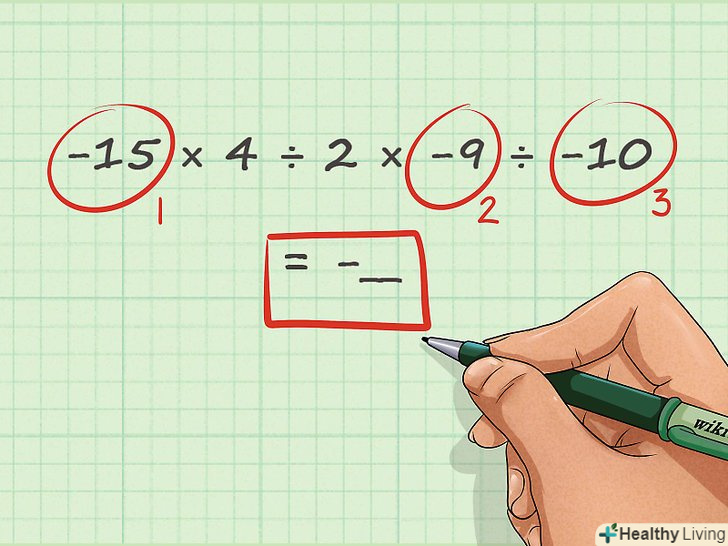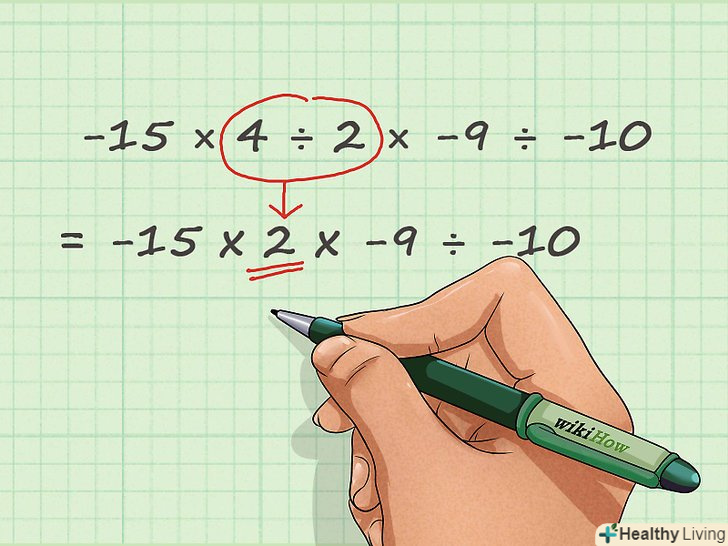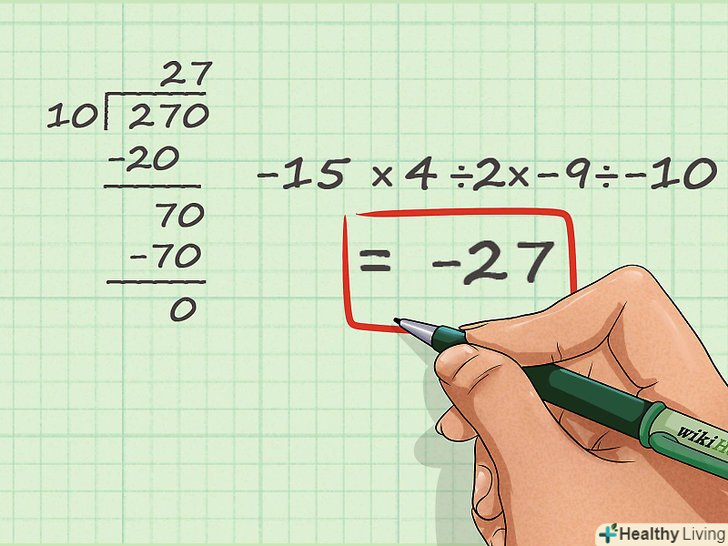Цілі позитивні або негативні цілі-це числа без десяткової або дробової частин. При множенні і діленні двох або більше цілих чисел ви можете використовувати таблицю множення і метод ділення / множення в стовпчик, і повинні стежити за знаком цілих чисел.
Кроки
Метод1З 3:
Загальна інформація
Метод1З 3:
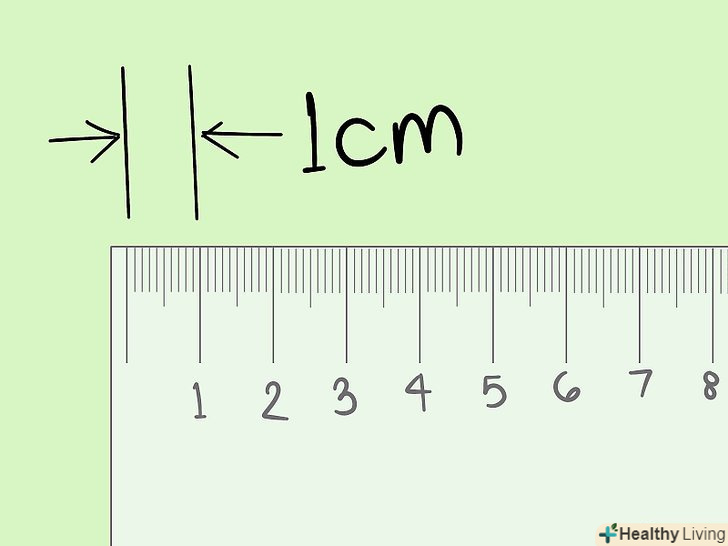
 Визначення цілих чисел. цілим є будь-яке число, яке може бути представлено без використання дробової або десяткової форми. Цілі числа можуть бути позитивними, негативними або рівними нулю. Наприклад, наступні числа є цілими числами: 1, 99, -217 і 0. Однак ці числа не є цілими: -10,4; 6¾; 2,1.
Визначення цілих чисел. цілим є будь-яке число, яке може бути представлено без використання дробової або десяткової форми. Цілі числа можуть бути позитивними, негативними або рівними нулю. Наприклад, наступні числа є цілими числами: 1, 99, -217 і 0. Однак ці числа не є цілими: -10,4; 6¾; 2,1.- Абсолютні значення можуть бути цілими числами (але не обов'язково). Абсолютне значення будь-якого числа дорівнює цьому числу без урахування його знака. Аналогічно, абсолютне значення даного числа є відстань від цього числа до нуля. Таким чином, абсолютне значення цілого числа завжди є цілим числом. Наприклад, абсолютне значення -12 дорівнює 12. Абсолютне значення 3 дорівнює 3. Абсолютне значення 0 дорівнює 0.
- Однак абсолютні значення чисел, які не є цілими, ніколи не будуть цілими числами. Наприклад, абсолютне значення 1/11 дорівнює 1/11 - дріб і, отже, не є цілим числом.
- Абсолютні значення можуть бути цілими числами (але не обов'язково). Абсолютне значення будь-якого числа дорівнює цьому числу без урахування його знака. Аналогічно, абсолютне значення даного числа є відстань від цього числа до нуля. Таким чином, абсолютне значення цілого числа завжди є цілим числом. Наприклад, абсолютне значення -12 дорівнює 12. Абсолютне значення 3 дорівнює 3. Абсолютне значення 0 дорівнює 0.
 Запам'ятайте таблицю множення. процес множення або ділення цілих чисел помітно прискорюється і спрощується в разі, якщо ви знаєте таблицю множення, тобто результат перемноження кожної пари чисел від 1 до 10. Як нагадування нижче наводиться основна таблиця множення. Цифри від 1 до 10 представлені у верхньому рядку і лівому стовпці таблиці; для отримання добутку двох чисел знайдіть осередок на перетині рядка і стовпця з потрібними цифрами (які ви множите).
Запам'ятайте таблицю множення. процес множення або ділення цілих чисел помітно прискорюється і спрощується в разі, якщо ви знаєте таблицю множення, тобто результат перемноження кожної пари чисел від 1 до 10. Як нагадування нижче наводиться основна таблиця множення. Цифри від 1 до 10 представлені у верхньому рядку і лівому стовпці таблиці; для отримання добутку двох чисел знайдіть осередок на перетині рядка і стовпця з потрібними цифрами (які ви множите).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Метод2 З 3:
Множення цілих чисел
Метод2 З 3:
 Підрахуйте кількість негативних чисел у вашому завданні.при множенні двох або більше позитивних чисел відповідь завжди буде позитивною. Але якщо в задачі кількість негативних чисел – парне, то результат буде позитивним; якщо в задачі кількість негативних чисел – непарне, то результат буде негативним. Тому перед початком множення цілих чисел підрахуйте кількість негативних чисел в задачі.
Підрахуйте кількість негативних чисел у вашому завданні.при множенні двох або більше позитивних чисел відповідь завжди буде позитивною. Але якщо в задачі кількість негативних чисел – парне, то результат буде позитивним; якщо в задачі кількість негативних чисел – непарне, то результат буде негативним. Тому перед початком множення цілих чисел підрахуйте кількість негативних чисел в задачі.- Наприклад: -10 × 5 × -11 × -20. У цьому завданні є три негативних числа. Ми будемо використовувати цю інформацію далі.
 Визначте знак вашої відповіді. як зазначено вище, при перемноженні тільки позитивних чисел відповідь завжди позитивний, але якщо в задачі присутні негативні числа, то відповідь або позитивний (парна кількість негативних чисел), або негативний (непарна кількість негативних чисел).
Визначте знак вашої відповіді. як зазначено вище, при перемноженні тільки позитивних чисел відповідь завжди позитивний, але якщо в задачі присутні негативні числа, то відповідь або позитивний (парна кількість негативних чисел), або негативний (непарна кількість негативних чисел).- У нашому прикладі є три негативних числа. Три-Непарне число, тому відповідь буде негативною. Ми можемо відразу написати знак мінус у відповіді (після знака одно), наприклад: -10 × 5 × -11 × -20 = - __
 Помножте числа від 1 до 10, використовуючи таблицю множення.твори будь-яких двох чисел менших або рівних 10 відображені в таблиці множення (див. У цьому випадку просто напишіть відповідь. Запам'ятайте: у завданнях на множення ви можете переміщати цілі числа для спрощення їх множення.
Помножте числа від 1 до 10, використовуючи таблицю множення.твори будь-яких двох чисел менших або рівних 10 відображені в таблиці множення (див. У цьому випадку просто напишіть відповідь. Запам'ятайте: у завданнях на множення ви можете переміщати цілі числа для спрощення їх множення.- У нашому прикладі результат множення 10х5 є в таблиці множення. Тут негативний знак (перед 10) не враховується, тому що ми вже знайшли знак остаточної відповіді. 10 × 5 = 50. Ми можемо підставити цей результат в нашу задачу: (50) × -11 × -20 = - __
- Якщо у вас виникли труднощі з розумінням процесу множення, подумайте про нього як про процес додавання. Наприклад, 5х10 є десять разів по п'ять. Іншими словами, 5 × 10 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5.
- У нашому прикладі результат множення 10х5 є в таблиці множення. Тут негативний знак (перед 10) не враховується, тому що ми вже знайшли знак остаточної відповіді. 10 × 5 = 50. Ми можемо підставити цей результат в нашу задачу: (50) × -11 × -20 = - __
 При необхідності розкладіть велике число на менші числа.якщо завдання включає числа більше десяти, не обов'язково використовувати множення в стовпчик. Для початку визначте, чи можна розкласти одне або кілька великих чисел на менші числа, а потім скористайтеся таблицею множення.
При необхідності розкладіть велике число на менші числа.якщо завдання включає числа більше десяти, не обов'язково використовувати множення в стовпчик. Для початку визначте, чи можна розкласти одне або кілька великих чисел на менші числа, а потім скористайтеся таблицею множення.- Розглянемо другу половину нашого прикладу: -11 x -20. Знаки не враховуються, тому що ми вже знайшли знак відповіді. 11 × 20 = (10 + 1) × 20= 10 × 20 + 1 × 20 = 10 × (2 × 10) + 1 × 20 = 2 × (10 × 10) + 1 × 20 = 220. Ми можемо підставити цей результат в нашу задачу: (50) × (220) = - __
 Для множення великих чисел використовуйтеМноження в стовпчик. якщо завдання включає два або кілька чисел більше 10, і ви не можете знайти відповідь через розкладання великих чисел на менші числа, то скористайтеся множенням в стовпчик. При множенні в стовпчик ви записуєте числа одне під іншим і множите кожну цифру нижнього числа на кожну цифру верхнього числа. Якщо нижнє число має дві і більше цифри, ви повинні записувати проміжні відповіді під одиницями, десятками, сотнями і так далі, додаючи нулі справа. Нарешті, щоб отримати остаточну відповідь, складіть всі проміжні відповіді.
Для множення великих чисел використовуйтеМноження в стовпчик. якщо завдання включає два або кілька чисел більше 10, і ви не можете знайти відповідь через розкладання великих чисел на менші числа, то скористайтеся множенням в стовпчик. При множенні в стовпчик ви записуєте числа одне під іншим і множите кожну цифру нижнього числа на кожну цифру верхнього числа. Якщо нижнє число має дві і більше цифри, ви повинні записувати проміжні відповіді під одиницями, десятками, сотнями і так далі, додаючи нулі справа. Нарешті, щоб отримати остаточну відповідь, складіть всі проміжні відповіді.- Повернемося до нашого прикладу. Тепер ми повинні помножити 50 на 220. Для цього скористаємося множенням в стовпчик. При множенні в стовпчик зверху напишіть більше число (220), а знизу – менше (50).
- Спочатку помножимо першу (праворуч) цифру нижнього числа на кожну цифру верхнього числа. Перша праворуч цифра числа 50 є 0 (знаходиться в розряді одиниць). 0 × 0 = 0, 0 × 2 = 0, 0 × 2 = 0. Іншими словами, 0 × 220 = 0. Напишіть цей перший проміжний відповідь в розряді одиниць.
- Далі ми помножимо другу (праворуч) цифру нижнього числа на кожну цифру верхнього числа. Друга праворуч цифра числа 50 є 5 (знаходиться в розряді десятків). Так як 5 знаходиться в розряді десятків, в розряді одиниць ми запишемо 0 (під першим проміжним відповіддю). Далі множимо: 5 × 0 = 0, 5 × 2 = 10 (тому напишіть 0 і запам'ятайте одиницю), 5х2 = 10 (тут напишіть не 10, а 11, так як до 10 ми додали 1, яку запам'ятали). Таким чином, другий проміжний відповідь: 11000.
- Далі ми просто складемо проміжні відповіді: 0 + 11000 = 11000. Так як відповідь є негативним числом, то запишемо: -10 × 5 × -11 × -20 = -11000.
- Повернемося до нашого прикладу. Тепер ми повинні помножити 50 на 220. Для цього скористаємося множенням в стовпчик. При множенні в стовпчик зверху напишіть більше число (220), а знизу – менше (50).
Метод3 З 3:
Розподіл цілих чисел
Метод3 З 3:
 Визначте знак відповіді залежно від кількості негативних чисел у вашому завданні. якщо в задачі кількість негативних чисел-парне (або їх взагалі немає), то результат буде позитивним; якщо в задачі кількість негативних чисел – непарне, то результат буде негативним.
Визначте знак відповіді залежно від кількості негативних чисел у вашому завданні. якщо в задачі кількість негативних чисел-парне (або їх взагалі немає), то результат буде позитивним; якщо в задачі кількість негативних чисел – непарне, то результат буде негативним.- Для прикладу розглянемо задачу, що включає як множення, так і ділення. У задачі -15 х 4 ÷ 2 х -9 ÷ -10 є три негативні числа, тому відповідь буде негативною. Таким чином, ми можемо відразу написати знак мінус у відповіді (після знака одно), наприклад: -15 × 4 ÷ 2 × -9 ÷ -10 = - __
 Розділіть малі числа, використовуючи таблицю множення. ділення-це зворотна операція для множення. При діленні одного числа на інше візьміть таблицю множення, знайдіть в ній осередок з великим числом (діленим), а потім знайдіть відповідні числа в рядку і стовпці, на перетині яких знаходиться знайдена комірка.
Розділіть малі числа, використовуючи таблицю множення. ділення-це зворотна операція для множення. При діленні одного числа на інше візьміть таблицю множення, знайдіть в ній осередок з великим числом (діленим), а потім знайдіть відповідні числа в рядку і стовпці, на перетині яких знаходиться знайдена комірка.- Давайте повернемося до нашого прикладу. У задачі -15 x 4 ÷ 2 x -9 ÷ -10 ми бачимо 4 ÷ 2. Знайдіть комірки з числом 4 в таблиці множення (їх дві) і відповідні числа: 4 х 1 = 4 і 2 х 2 = 4. Так як в нашій задачі 4 ділиться на 2, то ми вибираємо 2х2 = 4. Таким чином, 4 ÷ 2 = 2. Давайте перепишемо завдання як: -15 × (2) × -9 ÷ -10.
 Використовуйте ділення в стовпчик (якщо необхідно). якщо числа великі, і ви не можете розділити їх за допомогою таблиці множення, використовуйте ділення в стовпчик. Для цього напишіть ділене зліва, дільник – справа, а ПРИВАТНЕ (результат) записуйте під дільником (праворуч).
Використовуйте ділення в стовпчик (якщо необхідно). якщо числа великі, і ви не можете розділити їх за допомогою таблиці множення, використовуйте ділення в стовпчик. Для цього напишіть ділене зліва, дільник – справа, а ПРИВАТНЕ (результат) записуйте під дільником (праворуч).- Давайте використовуємо ділення в стовпчик в нашому прикладі. Ми можемо спростити наше завдання: -15 × (2) × -9 ÷ -10 = 270 ÷ -10. Ми ігноруємо знаки, оскільки ми вже знаємо знак остаточної відповіді. Напишіть 10 (дільник) справа, а 270 (ділене) - зліва.
- Розділимо першу цифру діленого на дільник: 2/10. 2 не ділиться на 10 (з цілою частиною), тому ми беремо перші дві цифри діленого і ділимо їх на дільник: 27/10 = 2 із залишком 7. Запишіть 2 під дільником-це перша цифра відповіді.
- Далі множимо першу цифру відповіді на дільник: 2х10 = 20. Записуємо 20 під першими двома цифрами діленого (27).
- Віднімаємо: 27-20 = 7 (перший залишок). Пишемо 7 під 0 (числа 20).
- Зносимо наступну цифру діленого і записуємо її поруч з першим залишком. Наступна цифра діленого є цифра 0. Пишемо її поруч з 7 і отримуємо 70.
- Розділимо отриману цифру на дільник: 70/10 = 7 без залишку. Пишемо 7 поруч з 2 (під дільником). Це друга цифра відповіді. Наша остаточна відповідь: 27.
- Зверніть увагу, що ми повинні врахувати залишок у випадку, якщо ділене не ділиться на дільник. Наприклад, якщо ми ділимо 271 (а не 270) на 10, то ми отримаємо залишок 1. В цьому випадку відповідь записуємо у вигляді: 27 (Ост.1).
- Давайте використовуємо ділення в стовпчик в нашому прикладі. Ми можемо спростити наше завдання: -15 × (2) × -9 ÷ -10 = 270 ÷ -10. Ми ігноруємо знаки, оскільки ми вже знаємо знак остаточної відповіді. Напишіть 10 (дільник) справа, а 270 (ділене) - зліва.
Поради
- При множенні числа можна переставляти місцями і групувати їх. Наприклад, завдання 15x3x6x2 можна переписати у вигляді 15x2x3x6 або(30) х (18).
- Запам'ятайте: завдання виду 15 х 2 х 0 х 3 х 6 завжди дорівнює нулю. Ви не повинні робити ніяких розрахунків.
- Зверніть увагу на порядок операцій. Дані правила поширюються на всі операції множення і / або ділення, але не додавання або віднімання.