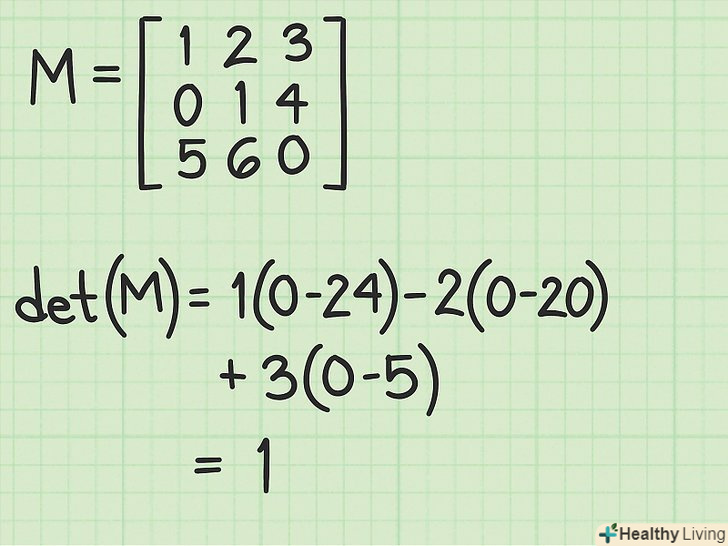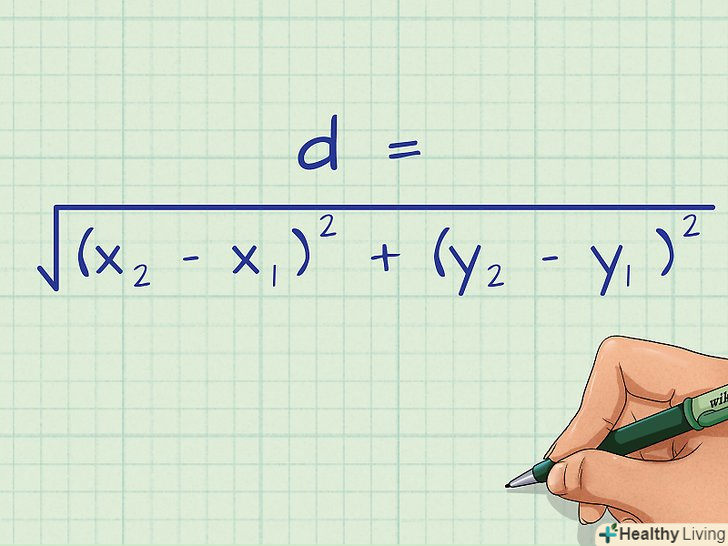Матриця ступінчастого виду по рядках використовується, наприклад, для геометричного представлення векторів, для вирішення систем лінійних рівнянь і для обчислення визначника матриці.
Кроки
- Зрозумійте, що являє собою матриця ступінчастого виду по рядках. ця така матриця, в якій під провідним елементом (першим ненульовим елементом) кожного рядка розташовуються виключно нулі. Якщо проаналізувати співвідношення між провідними елементами і їх розташуванням в матриці, можна багато чого зрозуміти про саму матриці. Ось приклад матриці ступінчастого виду по рядках.
- З'ясуйте, як виконувати елементарні операції з рядками. Такими операціями є:
- Перестановка рядків.
- Скалярне множення. Будь-який рядок може бути замінений ненульовим скалярним кратним цього рядка.
- Додавання рядків. Рядок може бути замінена сумою, отриманою від додавання цього рядка і кратним іншого рядка.
- Запишіть матрицю, яку потрібно привести до ступінчастого вигляду по рядках.
- Визначте перший провідний елемент матриці.провідні елементи необхідні для того, щоб зрозуміти, як скоротити рядки. Коли матриця буде приведена до ступінчастого виду по рядках, всі елементи, розташовані під провідними елементами, будуть рівні 0.
- У нашій матриці перший провідний елемент-це число в першому стовпці і першому рядку (тобто число у верхньому лівому «кутку» матриці). Провідний елемент не повинен дорівнювати 0. Якщо в даній вам матриці перший провідний елемент дорівнює 0, міняйте рядки, поки він не стане ненульовим.
- Пам'ятайте, що в одному стовпці і в одному рядку може бути тільки один провідний елемент. Якщо в якості такого елемента ви вибрали число в першому стовпці і в першому рядку, жоден інший елемент в цьому стовпці і в цьому рядку не може бути провідним.
- Виконайте операції з рядками матриці, щоб під першим провідним елементом отримати 0.
- У нашому прикладі замініть другий рядок на різницю цього рядка і першого рядка. Потім замініть третій рядок на різницю цього рядка і добуток 3 і першого рядка. Тобто виконайте наступні операції:
і
- У нашому прикладі замініть другий рядок на різницю цього рядка і першого рядка. Потім замініть третій рядок на різницю цього рядка і добуток 3 і першого рядка. Тобто виконайте наступні операції:
- Визначте Другий провідний елемент матриці. він розташовується праворуч від першого провідного елемента на наступних рядках, тобто другим провідним елементом може бути число в другому стовпці і другому рядку або число в другому стовпці і третьому рядку. У нашому прикладі в якості другого провідного елемента виберемо число в другому стовпці і другому рядку.
- Виконайте операції з рядками матриці, щоб під другим провідним елементом отримати 0.
- Вийшла матриця ступінчастого виду по рядках.
- Продовжіть знаходити провідні елементи і робити так, щоб під ними були 0.
Поради
- До ступінчастого виду по рядках можна привести матрицю будь-якого розміру (квадратну і прямокутну).