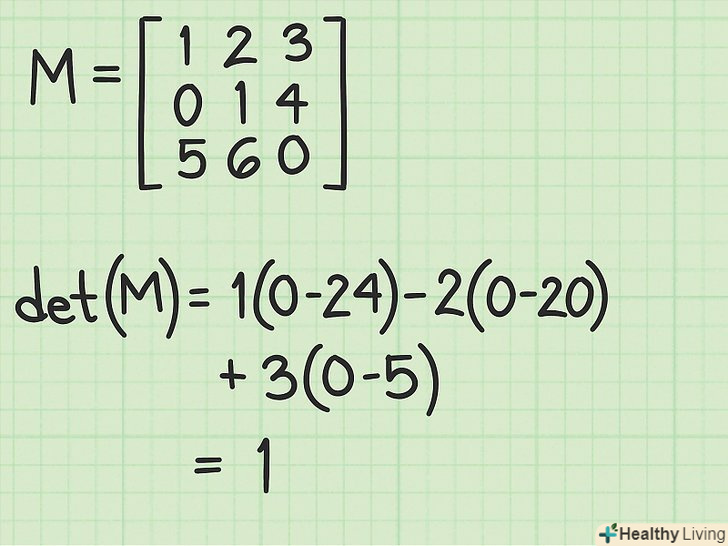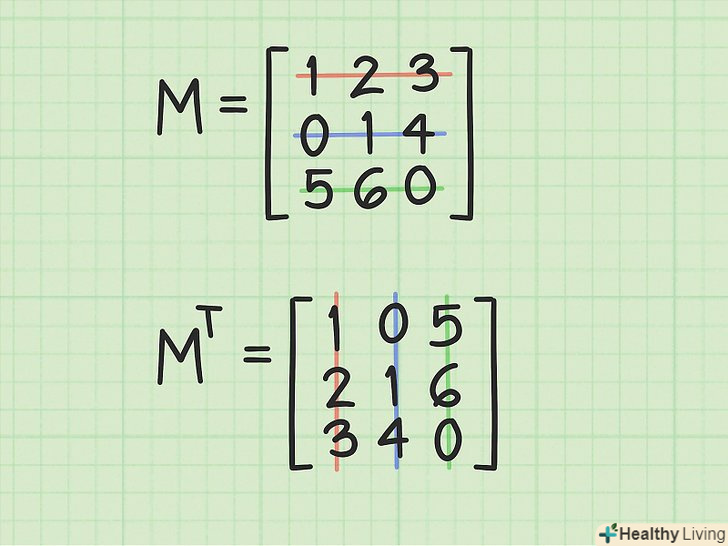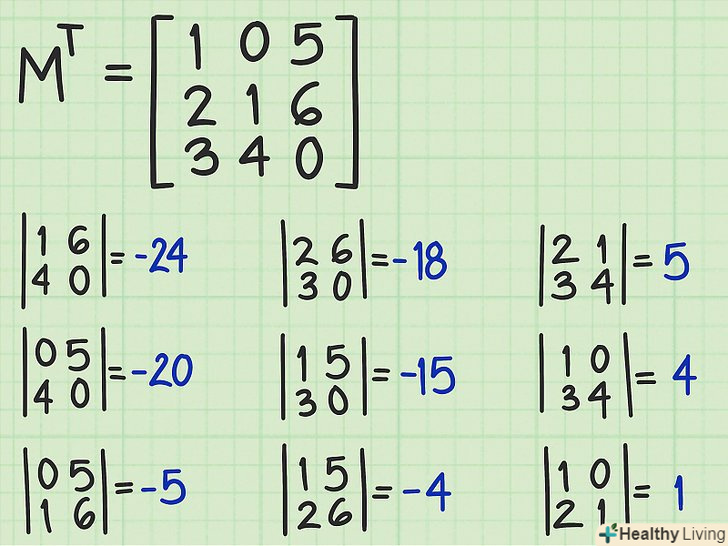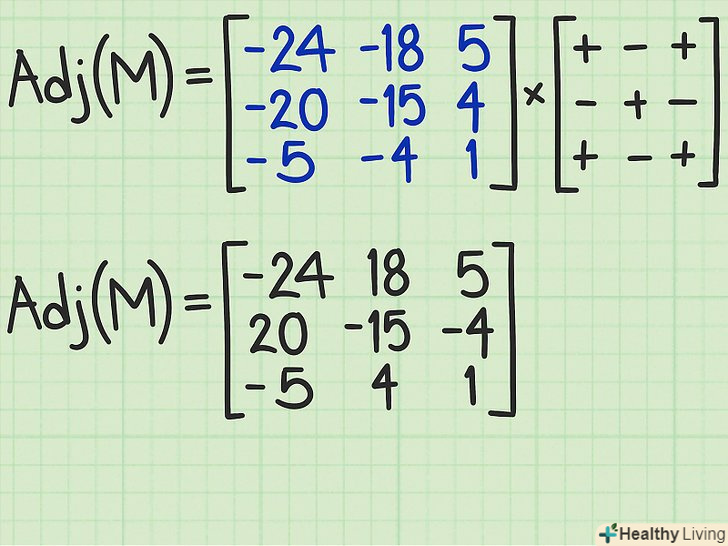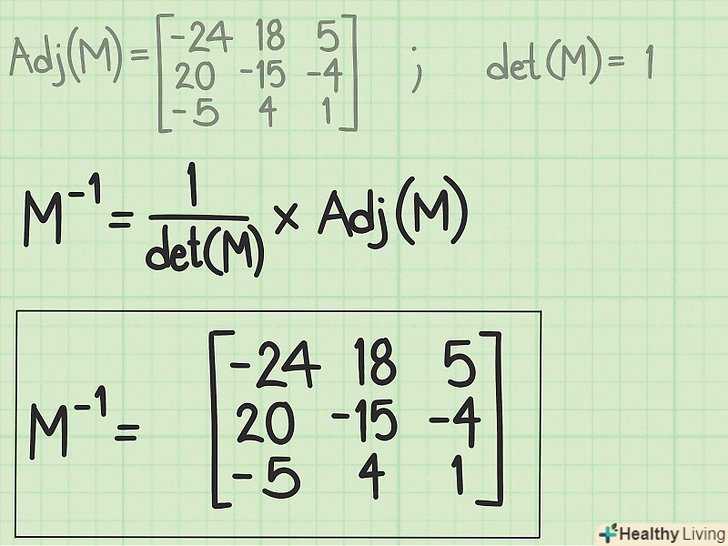Як правило, Зворотні операції використовуються для спрощення складних алгебраїчних виразів. Наприклад, якщо в задачі присутня операція ділення на дріб, можна замінити її операцією множення на зворотний дріб, що є зворотною операцією. Більш того, матриці ділити не можна, тому потрібно множити на зворотну матрицю. Обчислювати матрицю, зворотну матриці розміром 3х3, досить утомливо, але потрібно вміти робити це вручну. Також зворотну величину можна знайти за допомогою хорошого графічного калькулятора.
Кроки
Метод1З 3:
За допомогою приєднаної матриці
Метод1З 3:
 Перевірте визначник матриці. Спочатку обчисліть визначник матриці. Якщо визначник дорівнює 0, то зворотну матрицю обчислити не можна. Визначник матриці м позначається як det (М).[1]
Перевірте визначник матриці. Спочатку обчисліть визначник матриці. Якщо визначник дорівнює 0, то зворотну матрицю обчислити не можна. Визначник матриці м позначається як det (М).[1]- У разі матриці розміром 3х3 спочатку обов'язково обчисліть визначник.
- Щоб отримати детальну інформацію, прочитайте статтюяк знайти визначник матриці 3х3.
 Транспонуйте вихідну матрицю.транспонування-це Заміна рядків на стовпці щодо головної діагоналі матриці, тобто потрібно поміняти місцями елементи (i,j) і (j,i). При цьому елементи головної діагоналі (починається у верхньому лівому кутку і закінчується в нижньому правому куті) не змінюються.[2]
Транспонуйте вихідну матрицю.транспонування-це Заміна рядків на стовпці щодо головної діагоналі матриці, тобто потрібно поміняти місцями елементи (i,j) і (j,i). При цьому елементи головної діагоналі (починається у верхньому лівому кутку і закінчується в нижньому правому куті) не змінюються.[2]- Щоб поміняти рядки на стовпці, запишіть елементи першого рядка в першому стовпці, елементи другого рядка в другому стовпці, а елементи третього рядка в третьому стовпці. Порядок зміни положення елементів показаний на малюнку, на якому відповідні елементи обведені кольоровими кружками.
 Знайдіть визначити кожної матриці розміром 2х2. кожен елемент будь-якої матриці, включаючи транспоновану, пов'язаний з відповідною матрицею 2х2. Щоб знайти матрицю 2х2, яка відповідає певному елементу, закресліть рядок і стовпець, в яких знаходиться даний елемент, тобто потрібно закреслити п'ять елементів вихідної матриці 3х3. Незачеркнутими залишаться чотири елементи, які є елементами відповідної матриці 2х2.[3]
Знайдіть визначити кожної матриці розміром 2х2. кожен елемент будь-якої матриці, включаючи транспоновану, пов'язаний з відповідною матрицею 2х2. Щоб знайти матрицю 2х2, яка відповідає певному елементу, закресліть рядок і стовпець, в яких знаходиться даний елемент, тобто потрібно закреслити п'ять елементів вихідної матриці 3х3. Незачеркнутими залишаться чотири елементи, які є елементами відповідної матриці 2х2.[3]- Наприклад, щоб знайти матрицю 2х2 для елемента, який розташований на перетині другого рядка і першого стовпця, закресліть п'ять елементів, які знаходяться в другому рядку і першому стовпці. Решта чотири елементи є елементами відповідної матриці 2х2.
- Знайдіть визначник кожної матриці 2х2. Для цього твір елементів другорядної діагоналі відніміть з твору елементів головної діагоналі (дивіться малюнок).
- Детальну інформацію про матриці 2х2, відповідних певним елементам матриці 3х3, можна знайти в Інтернеті.
 Створіть матрицю кофакторів.результати, отримані раніше, запишіть у вигляді нової матриці кофакторів. Для цього знайдений визначник кожної матриці 2х2 напишіть там, де розташовувався відповідний елемент матриці 3х3. Наприклад, якщо розглядається матриця 2х2 для елемента (1,1), її визначник запишіть в позиції (1,1). Потім поміняйте знаки відповідних елементів згідно з певною схемою, яка показана на малюнку.[4]
Створіть матрицю кофакторів.результати, отримані раніше, запишіть у вигляді нової матриці кофакторів. Для цього знайдений визначник кожної матриці 2х2 напишіть там, де розташовувався відповідний елемент матриці 3х3. Наприклад, якщо розглядається матриця 2х2 для елемента (1,1), її визначник запишіть в позиції (1,1). Потім поміняйте знаки відповідних елементів згідно з певною схемою, яка показана на малюнку.[4]- Схема зміни знаків: знак першого елемента першого рядка не змінюється; знак другого елемента першого рядка змінюється на протилежний; знак третього елемента першого рядка не змінюється і так далі строково. Зверніть увагу, що знаки «+» і« -», які показані на схемі (дивіться малюнок), не свідчать про те, що відповідний елемент буде позитивним або негативним. В даному випадку знак » + « говорить про те, що знак елемента не змінюється, а знак » - " свідчить про зміну знака елемента.
- Детальну інформацію про матриці кофакторів можна знайти в Інтернеті.
- Так ви знайдете приєднану матрицю вихідної матриці. Іноді її називають комплексно-сполученої матрицею. Така матриця позначається як adj (M).
 Розділіть кожен елемент приєднаної матриці на визначник. визначник матриці М був обчислений на самому початку, щоб перевірити, що зворотна матриця існує. Тепер розділіть кожен елемент приєднаної матриці на цей визначник. Результат кожної операції ділення запишіть там, де знаходиться відповідний елемент. Так ви знайдете матрицю, зворотну вихідної.[5]
Розділіть кожен елемент приєднаної матриці на визначник. визначник матриці М був обчислений на самому початку, щоб перевірити, що зворотна матриця існує. Тепер розділіть кожен елемент приєднаної матриці на цей визначник. Результат кожної операції ділення запишіть там, де знаходиться відповідний елемент. Так ви знайдете матрицю, зворотну вихідної.[5]- Визначник матриці, яка показана на малюнку, дорівнює 1. Таким чином, тут приєднана матриця є зворотною матрицею (тому що при розподілі будь-якого числа на 1 воно не змінюється).
- У деяких джерелах операція ділення замінюється операцією множення на 1 / det(М). При цьому кінцевий результат не змінюється.
Метод2 З 3:
За допомогою елементарних перетворень
Метод2 З 3:
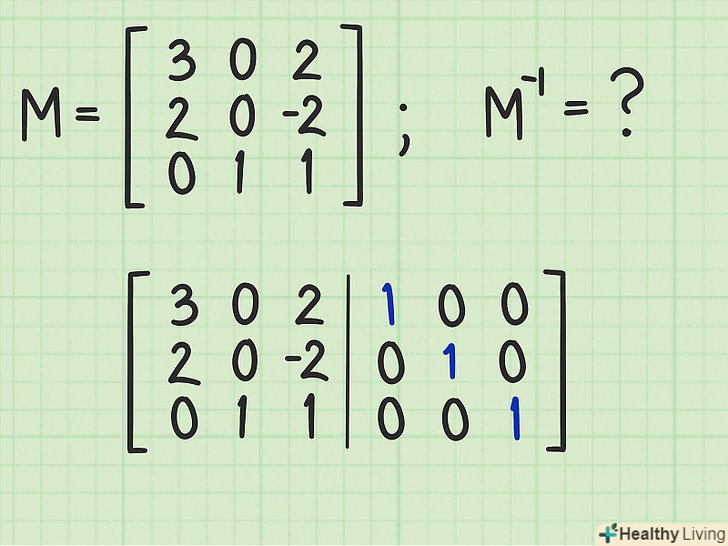
 Одиничну матрицю напишіть поруч з вихідною матрицею. запишіть вихідну матрицю М, праворуч від неї намалюйте вертикальну риску, а потім праворуч від риси запишіть одиничну матрицю. Вийде матриця з трьома рядками і шістьма стовпцями (велика матриця).[6]
Одиничну матрицю напишіть поруч з вихідною матрицею. запишіть вихідну матрицю М, праворуч від неї намалюйте вертикальну риску, а потім праворуч від риси запишіть одиничну матрицю. Вийде матриця з трьома рядками і шістьма стовпцями (велика матриця).[6]- Нагадаємо, що одиничною матрицею є матриця, де елементами головної діагоналі є одиниці, а іншими елементами є нулі. Детальну інформацію про одиничні матриці можна знайти в Інтернеті.
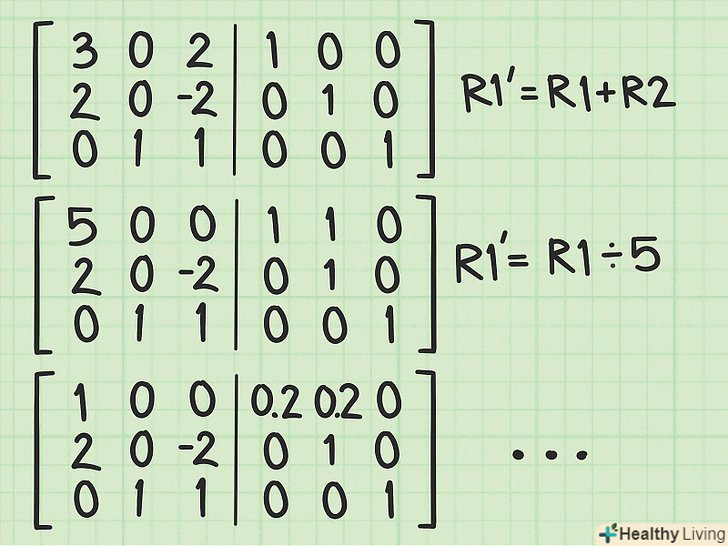
 Виконайте елементарні перетворення, щоб з вихідної матриці отримати одиничну.Наша мета полягає в тому, щоб створити одиничну матрицю на лівій половині великої матриці. Елементарні перетворення, що виконуються на лівій половині великої матриці, потрібно виконувати і на її правій половині (нагадаємо, що правою половиною великої матриці є одинична матриця).[7]
Виконайте елементарні перетворення, щоб з вихідної матриці отримати одиничну.Наша мета полягає в тому, щоб створити одиничну матрицю на лівій половині великої матриці. Елементарні перетворення, що виконуються на лівій половині великої матриці, потрібно виконувати і на її правій половині (нагадаємо, що правою половиною великої матриці є одинична матриця).[7]- Пам'ятайте, що елементарні перетворення включають в себе операції скалярного множення, а також додавання і віднімання рядків, щоб відокремити певні елементи. Детальну інформацію про елементарні перетворення матриць можна знайти в Інтернеті.
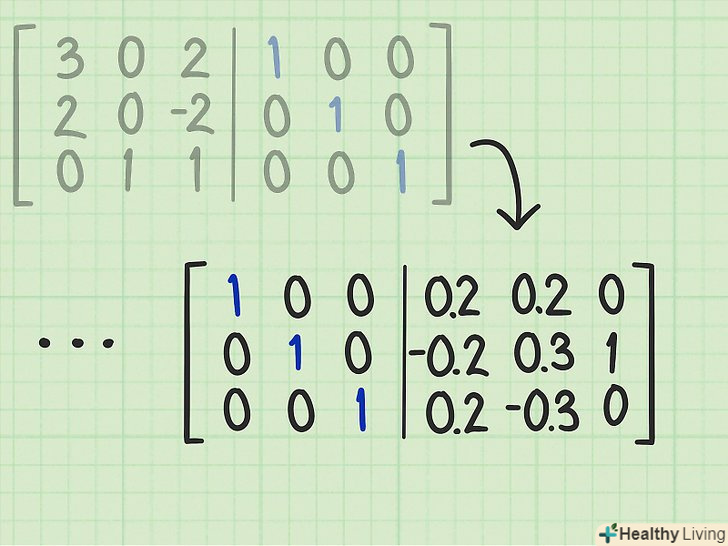
 Продовжуйте перетворювати велику матрицю до тих пір, поки її ліва половина (тобто вихідна матриця) не перетвориться в одиничну матрицю.нагадаємо, що одиничною матрицею є матриця, де елементами головної діагоналі є одиниці, а іншими елементами є нулі. Коли вихідна матриця стане одиничною, на правій половині великої матриці Ви отримаєте матрицю, зворотну вихідної.[8]
Продовжуйте перетворювати велику матрицю до тих пір, поки її ліва половина (тобто вихідна матриця) не перетвориться в одиничну матрицю.нагадаємо, що одиничною матрицею є матриця, де елементами головної діагоналі є одиниці, а іншими елементами є нулі. Коли вихідна матриця стане одиничною, на правій половині великої матриці Ви отримаєте матрицю, зворотну вихідної.[8] Запишіть зворотну матрицю.запишіть елементи, розташовані на правій половині великої матриці, у вигляді окремої матриці, яка є зворотною матрицею.[9]
Запишіть зворотну матрицю.запишіть елементи, розташовані на правій половині великої матриці, у вигляді окремої матриці, яка є зворотною матрицею.[9]
Метод3 З 3:
За допомогою калькулятора
Метод3 З 3:
 Виберіть калькулятор, який працює з матрицями.за допомогою простих калькуляторів не можна знайти зворотну матрицю, але це можна зробити на хорошому графічному калькуляторі, такому як Texas Instruments TI-83 або TI-86.[10]
Виберіть калькулятор, який працює з матрицями.за допомогою простих калькуляторів не можна знайти зворотну матрицю, але це можна зробити на хорошому графічному калькуляторі, такому як Texas Instruments TI-83 або TI-86.[10] Введіть вихідну матрицю в пам'ять калькулятора.для цього натисніть кнопку Matrix (матриця), якщо вона є. У разі калькулятора Texas Instruments, можливо, знадобиться натиснути кнопки 2nd і Matrix.
Введіть вихідну матрицю в пам'ять калькулятора.для цього натисніть кнопку Matrix (матриця), якщо вона є. У разі калькулятора Texas Instruments, можливо, знадобиться натиснути кнопки 2nd і Matrix. Виберіть меню Edit (редагування).зробіть це за допомогою кнопок зі стрілками або відповідної функціональної кнопки, яка знаходиться у верхній частині клавіатури калькулятора (розташування кнопки залежить від моделі калькулятора).[11]
Виберіть меню Edit (редагування).зробіть це за допомогою кнопок зі стрілками або відповідної функціональної кнопки, яка знаходиться у верхній частині клавіатури калькулятора (розташування кнопки залежить від моделі калькулятора).[11] Введіть позначення матриці. більшість графічних калькуляторів вміє працювати з 3-10 матрицями, які можна позначити буквами А-J. як правило, просто виберіть [A], щоб позначити вихідну матрицю. Потім натисніть кнопку Enter (введення).[12]
Введіть позначення матриці. більшість графічних калькуляторів вміє працювати з 3-10 матрицями, які можна позначити буквами А-J. як правило, просто виберіть [A], щоб позначити вихідну матрицю. Потім натисніть кнопку Enter (введення).[12] Введіть розмір матриці.у даній статті йдеться про матрицях 3х3. Але Графічні калькулятори вміють працювати з матрицями великих розмірів. Введіть кількість рядків, натисніть кнопку Enter, потім введіть кількість стовпців і ще раз натисніть кнопку Enter.[13]
Введіть розмір матриці.у даній статті йдеться про матрицях 3х3. Але Графічні калькулятори вміють працювати з матрицями великих розмірів. Введіть кількість рядків, натисніть кнопку Enter, потім введіть кількість стовпців і ще раз натисніть кнопку Enter.[13] Введіть кожен елемент матриці.на екрані калькулятора відобразиться матриця. Якщо раніше в калькулятор вже вводилася матриця, вона з'явиться на екрані. Курсор виділить перший елемент матриці. Введіть значення першого елемента і натисніть Enter. Курсор автоматично переміститься до наступного елементу матриці.[14]
Введіть кожен елемент матриці.на екрані калькулятора відобразиться матриця. Якщо раніше в калькулятор вже вводилася матриця, вона з'явиться на екрані. Курсор виділить перший елемент матриці. Введіть значення першого елемента і натисніть Enter. Курсор автоматично переміститься до наступного елементу матриці.[14]- Щоб ввести негативне значення елемента, натисніть спеціальну кнопку зі знаком "мінус", а не кнопку операції віднімання; в іншому випадку калькулятор не зможе правильно обробити це число.
- Щоб перейти до певного елементу матриці, скористайтеся кнопками зі стрілками.
 Вийдіть з режиму введення матриці.ввівши значення всіх елементів матриці, натисніть кнопку Quit (вихід). (Або, якщо необхідно, Натисніть кнопки 2nd і Quit.) Так ви вийдете з режиму введення матриці і перейдете на основний екран калькулятора.[15]
Вийдіть з режиму введення матриці.ввівши значення всіх елементів матриці, натисніть кнопку Quit (вихід). (Або, якщо необхідно, Натисніть кнопки 2nd і Quit.) Так ви вийдете з режиму введення матриці і перейдете на основний екран калькулятора.[15] Скористайтеся спеціальною кнопкою, щоб знайти зворотну матрицю. по-перше, увійдіть в режим введення матриці (натисніть кнопку Matrix) і натисніть кнопку Names (позначення), щоб вибрати позначення матриці, яке ви вказали раніше (швидше за все, [A]). Потім натисніть кнопку виконання зворотної операції, яка позначена як
Скористайтеся спеціальною кнопкою, щоб знайти зворотну матрицю. по-перше, увійдіть в режим введення матриці (натисніть кнопку Matrix) і натисніть кнопку Names (позначення), щоб вибрати позначення матриці, яке ви вказали раніше (швидше за все, [A]). Потім натисніть кнопку виконання зворотної операції, яка позначена як(можливо, спочатку доведеться натиснути кнопку 2nd). На екрані відобразиться
. Натисніть Enter, щоб вивести на екран зворотну матрицю.[16]
- Не користуйтеся кнопкою ^ (кнопка для зведення в ступінь), щоб ввести A^-1 за допомогою натискання декількох клавіш. Калькулятор не зрозуміє цю операцію.
- Якщо після натискання на кнопку зворотної операції на екрані відобразилося повідомлення про помилку, швидше за все, зворотна матриця не існує. Щоб переконатися в цьому, обчисліть визначити матриці.
 Перетворіть значення елементів зворотної матриці в звичайні дроби. за замовчуванням калькулятор відображає значення елементів зворотної матриці у вигляді десяткових дробів; в більшості випадків таку матрицю не можна записати у відповіді. Тому десяткові значення елементів зворотної матриці необхідно перетворити в звичайні дроби (в рідкісних випадках всі елементи зворотної матриці будуть цілими числами).[17]
Перетворіть значення елементів зворотної матриці в звичайні дроби. за замовчуванням калькулятор відображає значення елементів зворотної матриці у вигляді десяткових дробів; в більшості випадків таку матрицю не можна записати у відповіді. Тому десяткові значення елементів зворотної матриці необхідно перетворити в звичайні дроби (в рідкісних випадках всі елементи зворотної матриці будуть цілими числами).[17]- У багатьох графічних калькуляторах є кнопка, що дозволяє перетворювати десяткові дроби в звичайні. Наприклад, на калькуляторі TI-86 натисніть Math (Математика), виберіть Misc (інше), потім виберіть Frac (дріб) і натисніть Enter. Десяткові дроби будуть автоматично перетворені в звичайні.
Поради
- Описані методи можна застосовувати до матриць, елементами яких є не тільки числа, але і змінні, невідомі і навіть алгебраїчні вирази.
- Обчислення записуйте на папері, так як знайти зворотну матрицю в розумі вкрай складно.
- Існують комп'ютерні програми, які вміють працювати з будь-якими матрицями[18], включаючи матриці 30х30.
- Перевірте відповідь, отриману за допомогою будь-якого з описаних у цій статті методів. Для цьогоперемножте вихідну (М) і зворотну (м1) матриці. Пам'ятайте, що М * м1 = м1*М = 1. Одинична матриця-це матриця, де елементами головної діагоналі є одиниці, а іншими елементами є нулі. Якщо результат перемноження не дорівнює 1, Перевірте ваші обчислення.
Попередження
- Не всі матриці 3x3 оборотні. Якщо визначник матриці дорівнює 0, зворотна матриця не існує. (Зверніть увагу, що в обчисленнях присутній поділ на визначник, а на 0 ділити не можна.)
Джерела
- ↑ Https://www.mathsisfun.com/algebra/matrix-inverse-minors-cofactors-adjugate.html
- ↑ Http://www.mathcentre.ac.uk/resources/uploaded/sigma-matrices11-2009-1.pdf
- ↑ Http://www.mathwords.com/c/cofactor_matrix.htm
- ↑ Http://www.mathwords.com/c/cofactor_matrix.htm
- ↑ Http://mathworld.wolfram.com/MatrixInverse.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- <= Http://www.bluebyte.gr/matrix-calculator/