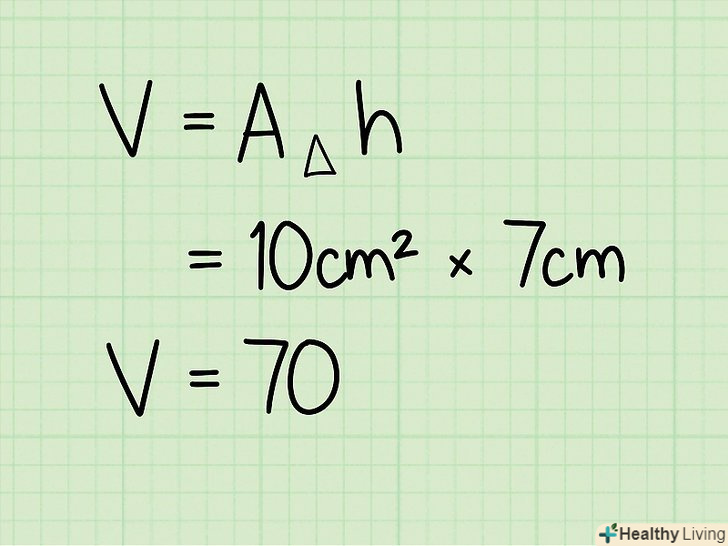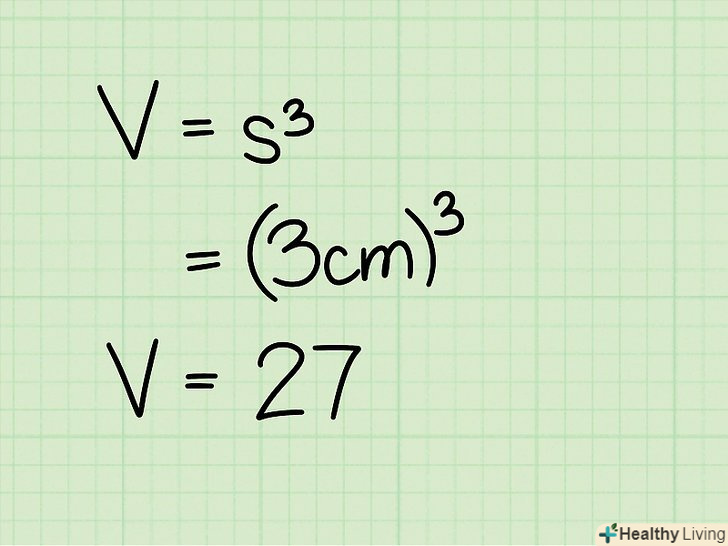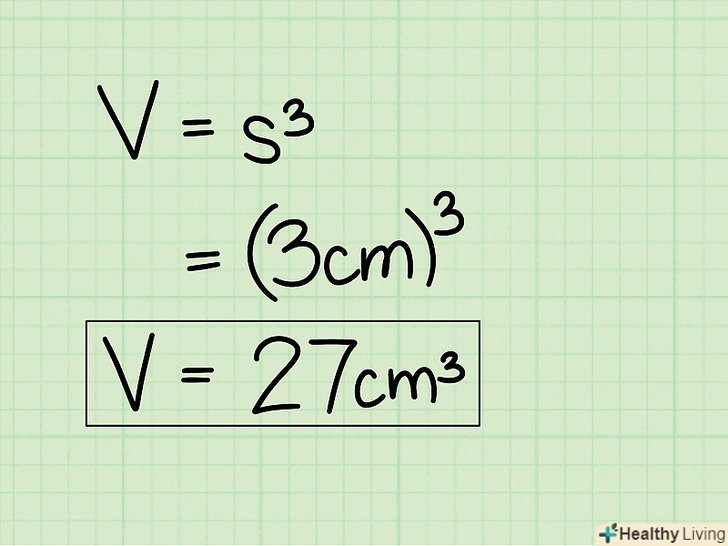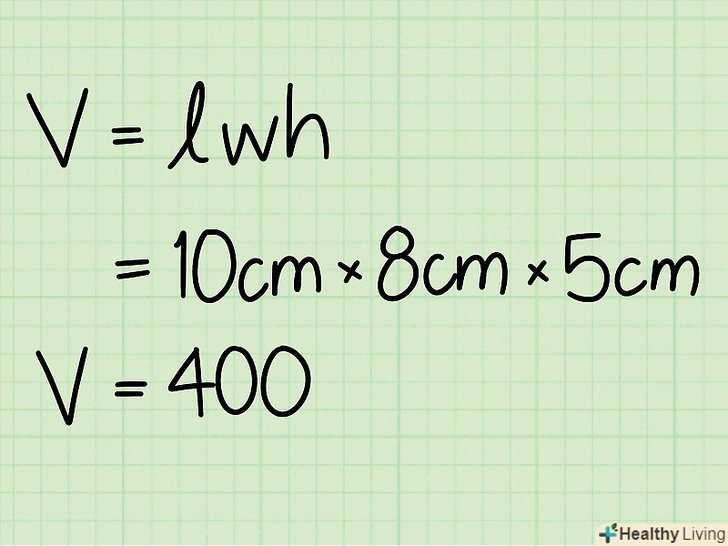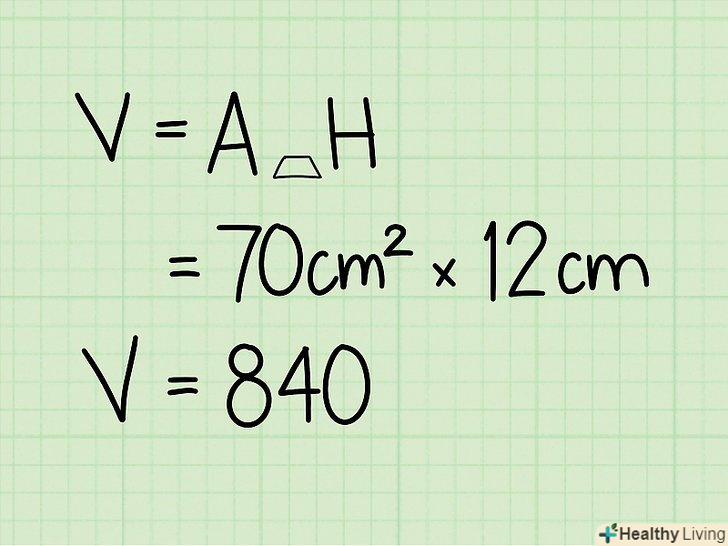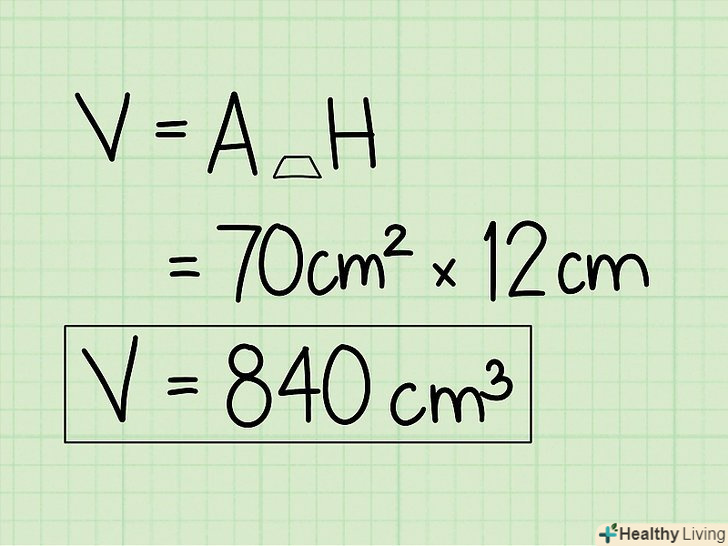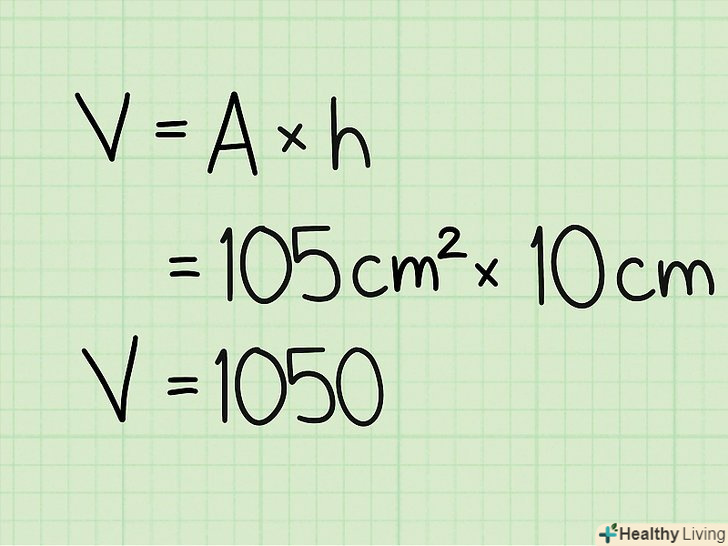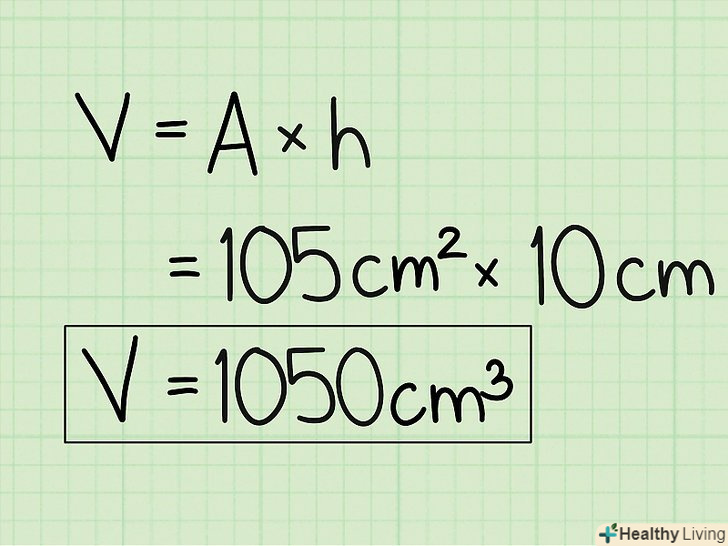Призма-об'ємна геометрична фігура з двома рівними підставами і плоскими гранями. Призму називають за формою її заснування; так призми з трикутною основою називають "трикутною призмою". Щоб знайти обсяг призми, потрібно просто обчислити площу її підстави і помножити його на її висоту; проте обчислення площі підстави може бути нетривіальним завданням. Ось як можна обчислити обсяг різних призм.
Кроки
Метод1З 5:
Обчислення об'єму трикутної призми
Метод1З 5:
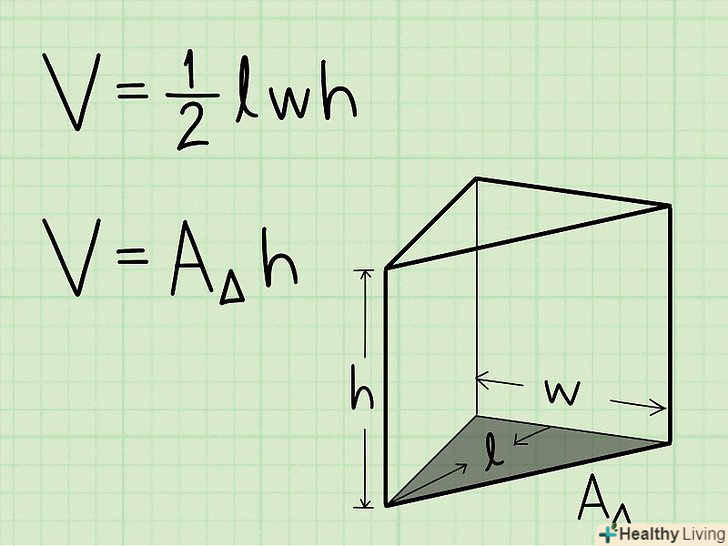
 Запишіть формулу для знаходження об'єму трикутної призми. Формула проста:V = площа основи призми х висота призми. Ви можете знайти площу підстави за формулою для знаходження площі трикутника - 1/2 помножити на сторону і помножити на висоту.
Запишіть формулу для знаходження об'єму трикутної призми. Формула проста:V = площа основи призми х висота призми. Ви можете знайти площу підстави за формулою для знаходження площі трикутника - 1/2 помножити на сторону і помножити на висоту. Знайдіть площу основи. щоб обчислити об'єм трикутної призми, необхідно спочатку знайти площу трикутника, що лежить в основі. Знайдіть площу основи призми (в даному випадку трикутника) шляхом множення 1/2 на сторону трикутника і на його висоту.[1]
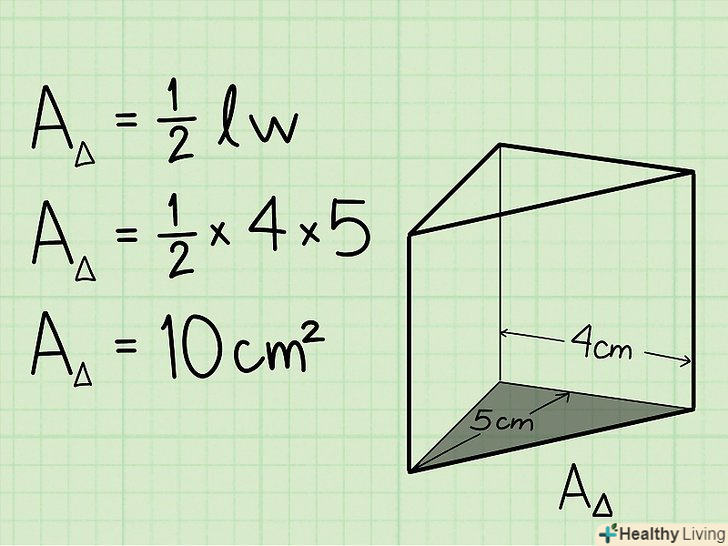
Знайдіть площу основи. щоб обчислити об'єм трикутної призми, необхідно спочатку знайти площу трикутника, що лежить в основі. Знайдіть площу основи призми (в даному випадку трикутника) шляхом множення 1/2 на сторону трикутника і на його висоту.[1]- Наприклад, якщо висота трикутника дорівнює 5 см, а його сторона дорівнює 4 см, то площа підстави дорівнює 1/2 х 5 см х 4 см = 10 см2.
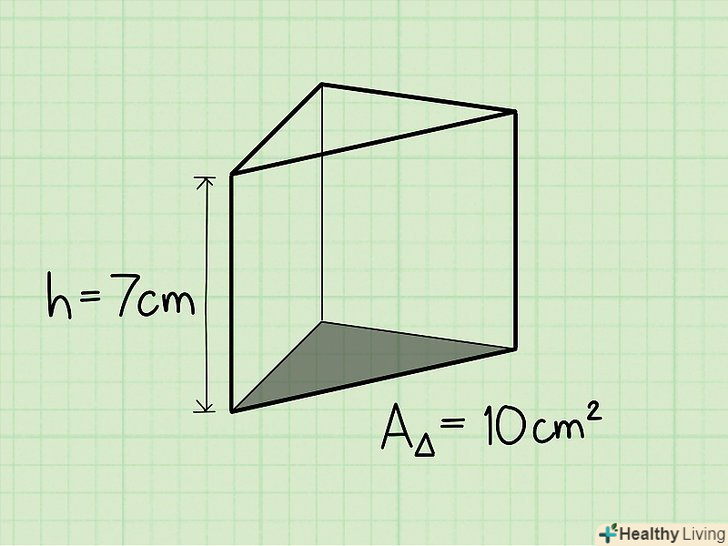
 Знайдіть висоту.припустимо, висота трикутної призми дорівнює 7 см.
Знайдіть висоту.припустимо, висота трикутної призми дорівнює 7 см. Помножте площу основи (трикутника) на висоту призми.після того, як ви помножите площу на висоту, ви отримаєте об'єм трикутної призми.
Помножте площу основи (трикутника) на висоту призми.після того, як ви помножите площу на висоту, ви отримаєте об'єм трикутної призми.- Для нашого прикладу: 10 см2 x 7 см = 70 см3.
 Запишіть відповідь у кубічних одиницях.при розрахунку обсягу слід завжди використовувати кубічні одиниці виміру, так як робота ведеться з тривимірними об'єктами. Остаточна відповідь 70 см3.
Запишіть відповідь у кубічних одиницях.при розрахунку обсягу слід завжди використовувати кубічні одиниці виміру, так як робота ведеться з тривимірними об'єктами. Остаточна відповідь 70 см3.
Метод2З 5:
Обчислення об'єму куба
Метод2З 5:
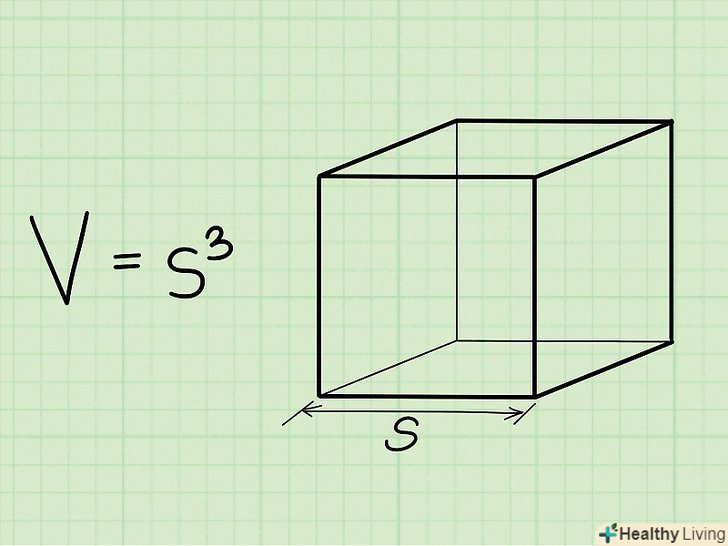
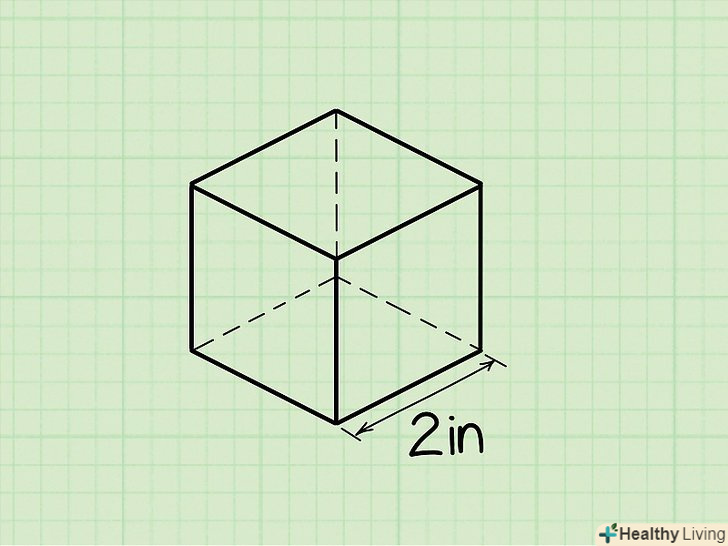
 Запишіть формулу для знаходження об'єму куба. Формула проста: V = (довжина ребра)3 Куб являє собою призму, у якій всі ребра рівні.[2]
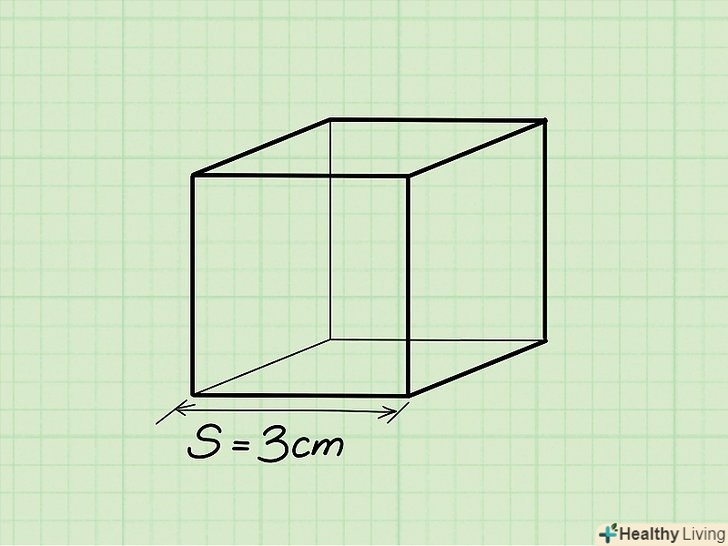
Запишіть формулу для знаходження об'єму куба. Формула проста: V = (довжина ребра)3 Куб являє собою призму, у якій всі ребра рівні.[2] Знайдіть довжину ребра куба.всі ребра рівні, тому неважливо, яке ребро розглядати.
Знайдіть довжину ребра куба.всі ребра рівні, тому неважливо, яке ребро розглядати.- Наприклад: довжина ребра = 3 см.
 Зведіть довжину в куб.для зведення в куб просто двічі помножте число на саме себе. Наприклад, куб "а « - це»а x а x а". Оскільки всі довжини ребер куба рівні, вам не потрібно обчислювати площу підстави і множити його на висоту. Перемноження будь-яких двох ребер куба дасть вам площі підстави, а будь-яке третє ребро може представляти висоту. Вам не потрібно замислюватися над перемноженням довжини, ширини і висоти, так як в кубі цими величинами може бути будь-яке ребро.
Зведіть довжину в куб.для зведення в куб просто двічі помножте число на саме себе. Наприклад, куб "а « - це»а x а x а". Оскільки всі довжини ребер куба рівні, вам не потрібно обчислювати площу підстави і множити його на висоту. Перемноження будь-яких двох ребер куба дасть вам площі підстави, а будь-яке третє ребро може представляти висоту. Вам не потрібно замислюватися над перемноженням довжини, ширини і висоти, так як в кубі цими величинами може бути будь-яке ребро.- Наприклад: 3 см3 = 3 см * 3 см * 3 см = 27 см3.
 Запишіть відповідь у кубічних одиницях.не забудьте записати остаточну відповідь в кубічних одиницях. У нашому випадку остаточна відповідь: 27 см3.
Запишіть відповідь у кубічних одиницях.не забудьте записати остаточну відповідь в кубічних одиницях. У нашому випадку остаточна відповідь: 27 см3.
Метод3З 5:
Обчислення об'єму прямокутної призми
Метод3З 5:
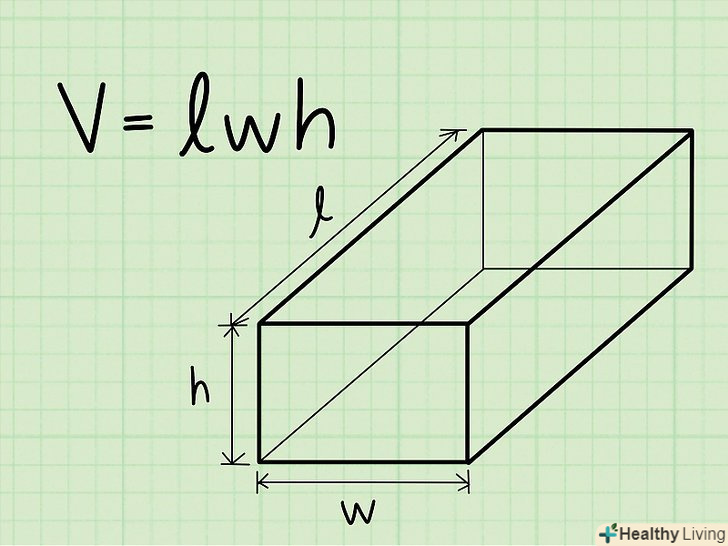
 Запишіть формулу для знаходження об'єму прямокутної призми. Формула: V = довжина * ширина * висота прямокутна призма-призма з прямокутною основою.
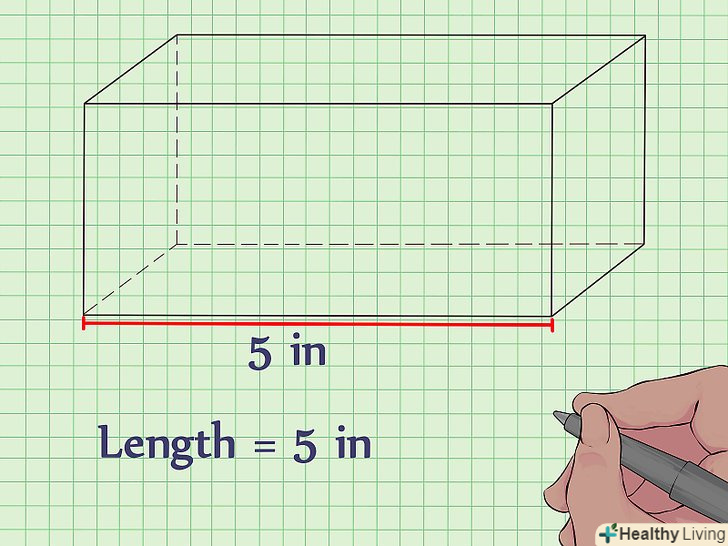
Запишіть формулу для знаходження об'єму прямокутної призми. Формула: V = довжина * ширина * висота прямокутна призма-призма з прямокутною основою. Знайдіть довжину.довжина прямокутної призми-довга сторона прямокутника, що лежить в основі призми.
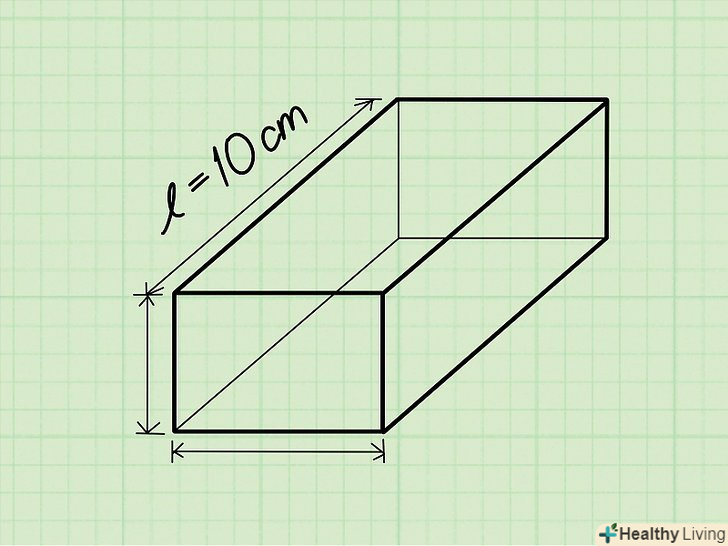
Знайдіть довжину.довжина прямокутної призми-довга сторона прямокутника, що лежить в основі призми.- Наприклад: довжина = 10 см.
 Знайдіть ширину.ширина прямокутної призми-коротка сторона прямокутника, що лежить в основі призми.
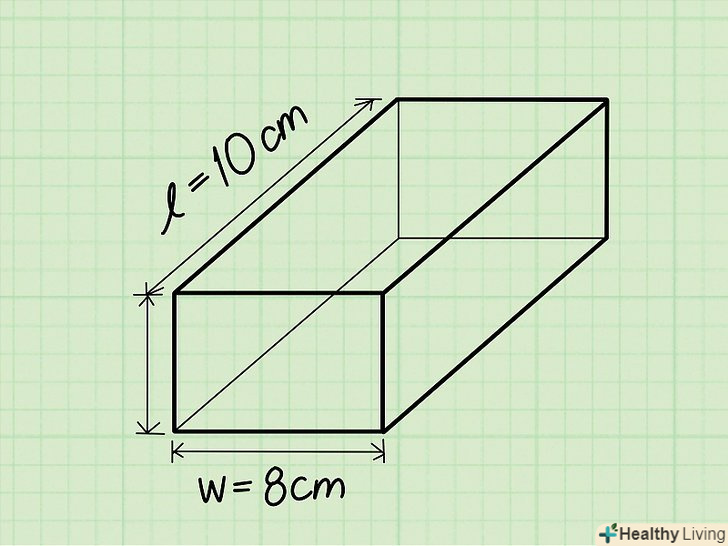
Знайдіть ширину.ширина прямокутної призми-коротка сторона прямокутника, що лежить в основі призми.- Наприклад: ширина = 8 см.
 Знайдіть висоту.висота прямокутної призми - будь-яка грань, перперндікулярная основи (грань, що піднімається вгору). Ви можете уявити собі висоту прямокутної призми як грань, яка простягається вгору від основи до верхнього плоского прямокутник і робить фігуру тривимірною.
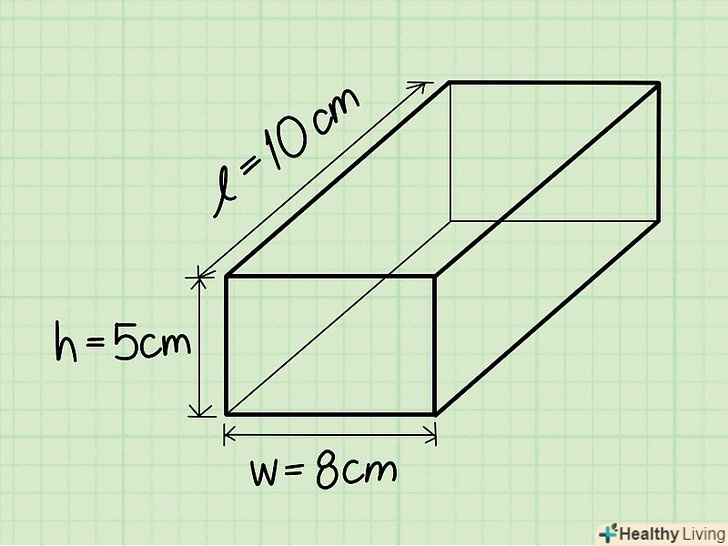
Знайдіть висоту.висота прямокутної призми - будь-яка грань, перперндікулярная основи (грань, що піднімається вгору). Ви можете уявити собі висоту прямокутної призми як грань, яка простягається вгору від основи до верхнього плоского прямокутник і робить фігуру тривимірною.- Наприклад: Висота = 5 см.
 Перемножте довжину, ширину і висоту.ви можете помножити їх в будь-якому порядку і отримаєте той же результат. За допомогою цього методу ви, по суті, обчислюєте площу прямокутного підстави (10 х 8 ), а потім множите його на висоту (5). Тому для знаходження обсягу цієї призми можна помножити довжини ребер в будь-якому порядку.
Перемножте довжину, ширину і висоту.ви можете помножити їх в будь-якому порядку і отримаєте той же результат. За допомогою цього методу ви, по суті, обчислюєте площу прямокутного підстави (10 х 8 ), а потім множите його на висоту (5). Тому для знаходження обсягу цієї призми можна помножити довжини ребер в будь-якому порядку.- Наприклад: 10 см * 8 см * 5 см = 400 см3.
 Запишіть відповідь у кубічних одиницях. остаточна відповідь: 400 см3 .
Запишіть відповідь у кубічних одиницях. остаточна відповідь: 400 см3 .
Метод4З 5:
Обчислення об'єму трапецеїдальної призми
Метод4З 5:
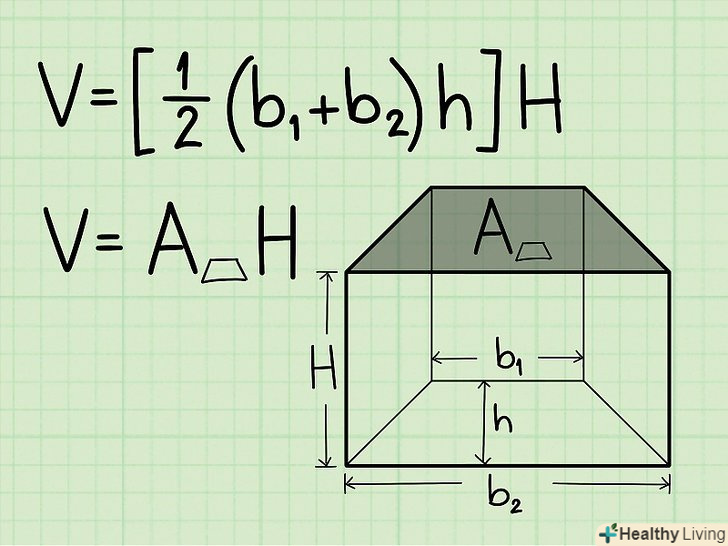
 Запишіть формулу для обчислення об'єму трапецеїдальної призми. Формула: V = [1/2 x (підстава трапеції1 + підстава трапеції2) x висота трапеції] x висота призми. Перш ніж обчислювати обсяг призми, необхідно використовувати першу частину цієї формули, щоб знайти площу підстави призми (площа трапеції).[3]
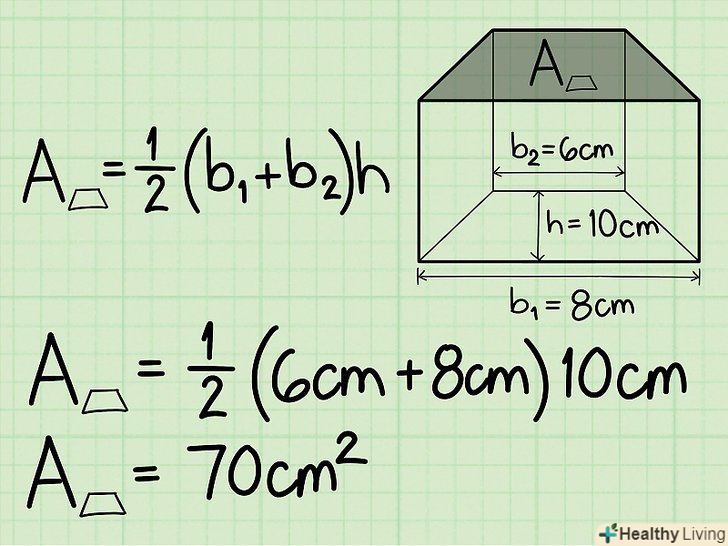
Запишіть формулу для обчислення об'єму трапецеїдальної призми. Формула: V = [1/2 x (підстава трапеції1 + підстава трапеції2) x висота трапеції] x висота призми. Перш ніж обчислювати обсяг призми, необхідно використовувати першу частину цієї формули, щоб знайти площу підстави призми (площа трапеції).[3] Знайдіть площу основи трапецеїдальної призми.для цього просто підставте в формулу довжину обох підстави і висоту трапеції.
Знайдіть площу основи трапецеїдальної призми.для цього просто підставте в формулу довжину обох підстави і висоту трапеції.- Наприклад, підстава1 = 8 см, підстава2 = 6 см, а висота = 10 см.
- 1/2 х ( 6 + 8 ) х 10 = 1/2 х 14 см х 10 см = 70 см2.
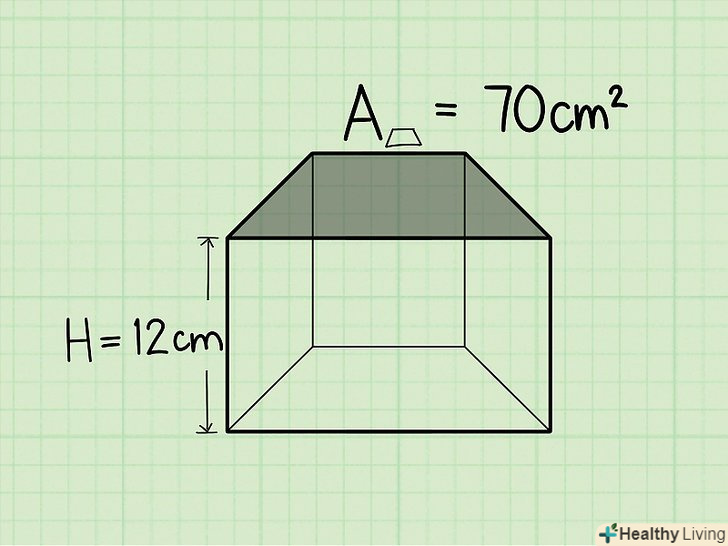
 Знайдіть висоту трапецеїдальної призми.припустимо, висота трапецеїдальної призми становить 12 см.
Знайдіть висоту трапецеїдальної призми.припустимо, висота трапецеїдальної призми становить 12 см. Помножте площу основи на висоту.щоб розрахувати обсяг трапецеїдальної призми, треба просто помножити площу підстави на висоту.
Помножте площу основи на висоту.щоб розрахувати обсяг трапецеїдальної призми, треба просто помножити площу підстави на висоту.- 70 см2 x 12 см = 840 см3.
 Запишіть відповідь у кубічних одиницях. остаточна відповідь: 840 см3 .
Запишіть відповідь у кубічних одиницях. остаточна відповідь: 840 см3 .
Метод5З 5:
Обчислення обсягу правильної п'ятикутної призми
Метод5З 5:
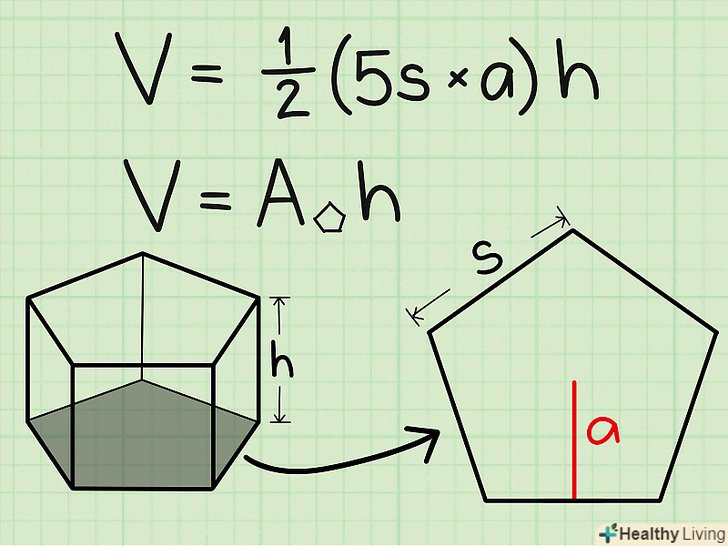
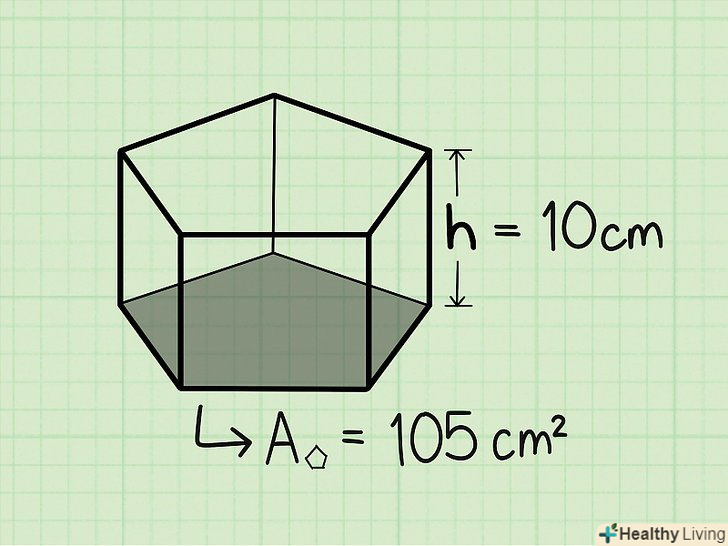
 Запишіть формулу для знаходження об'єму п'ятикутної призми. Формула: V = [1/2 x 5 x сторона п'ятикутника x апофема] x висота призми. Можна використовувати першу частину формули для знаходження площі п'ятикутника в основі призми. Це можна уявити як знаходження площі п'яти трикутників, що складають правильний п'ятикутник. В цьому випадку сторона п'ятикутника дорівнює підставі трикутника, а апофема — висоті трикутника. Помножимо ці величини на 1/2 і отримаємо площу трикутника, а потім помножимо результат на 5, так як 5 однакових трикутників складають основу правильної п'ятикутної призми.[4]
Запишіть формулу для знаходження об'єму п'ятикутної призми. Формула: V = [1/2 x 5 x сторона п'ятикутника x апофема] x висота призми. Можна використовувати першу частину формули для знаходження площі п'ятикутника в основі призми. Це можна уявити як знаходження площі п'яти трикутників, що складають правильний п'ятикутник. В цьому випадку сторона п'ятикутника дорівнює підставі трикутника, а апофема — висоті трикутника. Помножимо ці величини на 1/2 і отримаємо площу трикутника, а потім помножимо результат на 5, так як 5 однакових трикутників складають основу правильної п'ятикутної призми.[4] Знайдіть площу п'ятикутної основи.припустимо, довжина сторони становить 6 см і довжина апофеми дорівнює 7 см. Просто підставте ці цифри в формулу:
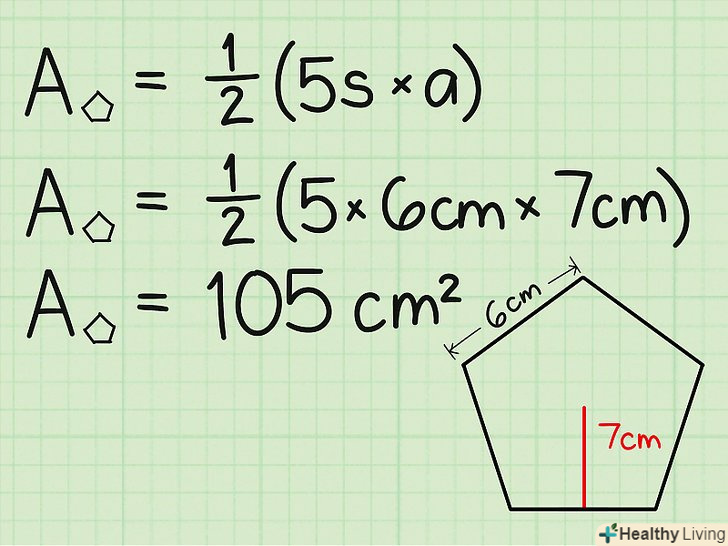
Знайдіть площу п'ятикутної основи.припустимо, довжина сторони становить 6 см і довжина апофеми дорівнює 7 см. Просто підставте ці цифри в формулу:- А = 1/2 х 5 х сторона х апофема.
- А= 1/2 х 5 х 6 см х 7 см = 105 см2.
 Знайдіть висоту призми.припустимо, висота призми дорівнює 10 см.
Знайдіть висоту призми.припустимо, висота призми дорівнює 10 см. Помножте площу п'ятикутної основи на висоту призми. просто помножте площу підстави (105 см2) на висоту (10 см) і знайдете обсяг правильної п'ятикутної призми.
Помножте площу п'ятикутної основи на висоту призми. просто помножте площу підстави (105 см2) на висоту (10 см) і знайдете обсяг правильної п'ятикутної призми.- 105 см2 x 10 см = 1050 см3.
 Запишіть відповідь у кубічних одиницях. остаточна відповідь: 1050 см3 .
Запишіть відповідь у кубічних одиницях. остаточна відповідь: 1050 см3 .
Поради
- Постарайтеся не плутати "підстава призми»з "підставою фігури". Підстава призми - це двомірна фігура, яка утворює основу всієї призми (як правило, її верхня і нижня грань). Але ця двомірна фігура може мати своє власне підставу-сторону, на яку опускається перпендикуляр і яка допомагає обчислити площу двомірної фігури.
Джерела
- ↑ Http://www.cimt.plymouth.ac.uk/projects/mepres/book7/bk7i22/bk7_22i6.htm
- ↑ Http://www.basic-mathematics.com/volume-of-a-cube.html
- ↑ Http://www.mathgoodies.com/lessons/vol1/area_trapezoid.html
- ↑ Http://www.wikicalculator.com/formula_calculator/Volume-Area-of-Pentagonal-Prism-130.htm
- ↑ Http://www.mathopenref.com/apothem.html