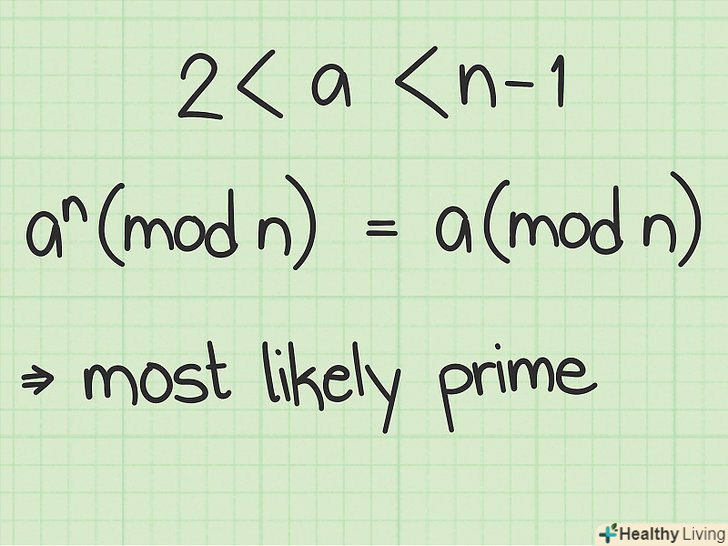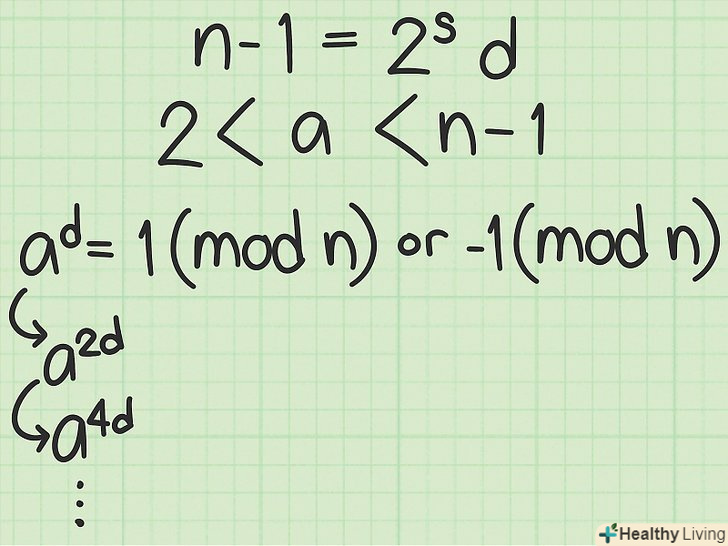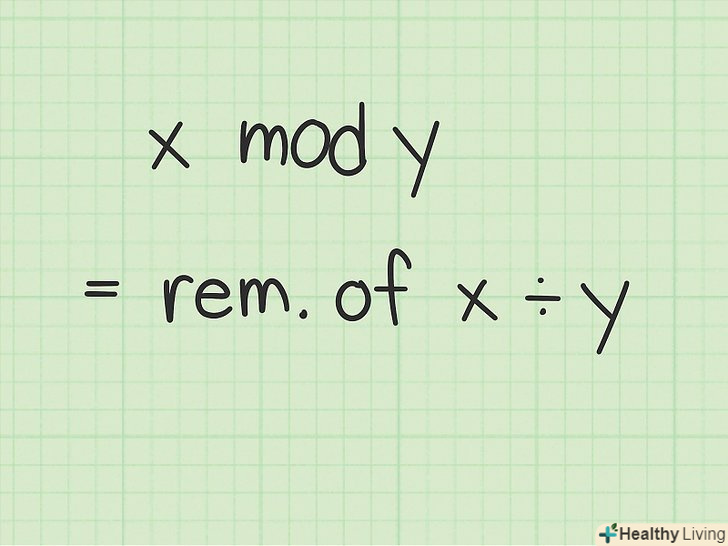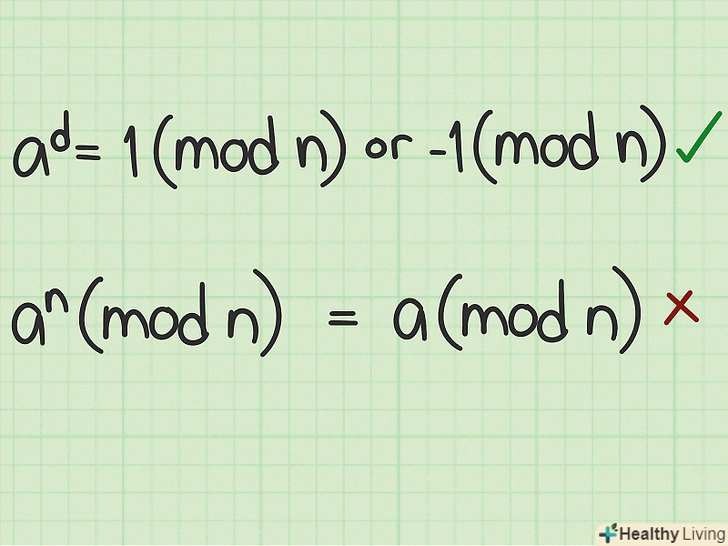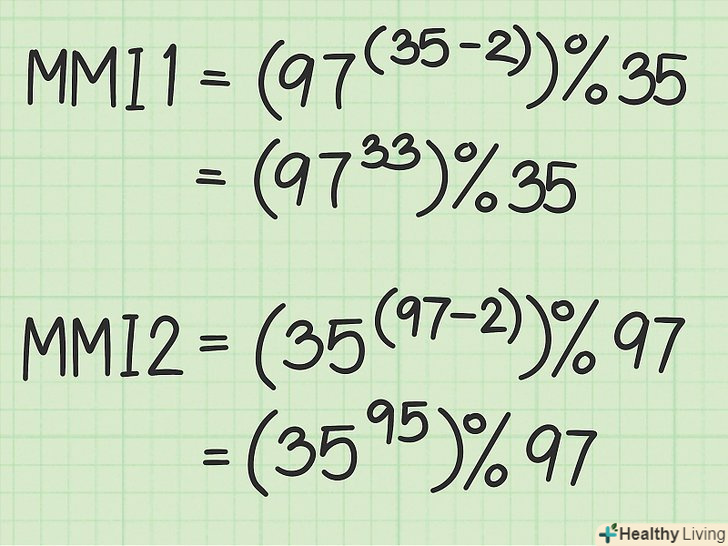1. Головна
    2. Математика
    3. Як перевірити, чи є число простим

Як перевірити, чи є число простим

Прості числа-це числа, які діляться тільки на себе і на 1. Всі інші числа називаються складовими числами. Є безліч способів визначити, чи є число простим, і всі вони мають свої переваги і недоліки. З одного боку, деякі методи відрізняються великою точністю, але вони досить складні, якщо ви маєте справу з великими числами. З іншого боку, існують набагато швидші способи, але вони можуть призвести до неправильних результатів. Вибір відповідного методу залежить від того, з наскільки великими числами ви працюєте.

Частина1З 3:
Тести простоти

Примітка: у всіх формулахn позначає перевіряється число.

  1. Перебір дільників. достатньо поділити n на всі прості числа від 2 до округленого значення (N{\displaystyle {\sqrt {n}}}).
  2. Мала теорема Ферма. попередження: іноді тест помилково ідентифікує складові числа як прості, навіть для всіх величин A.
    • Виберемо ціле число a, таке що 2 ≤ a ≤ n - 1.
    • Якщо an (mod n) = a (mod n), то число, ймовірно, просте. Якщо рівність не виконується, число n є складовим.
    • Перевірте дану рівність для декількох значеньa, щоб збільшити ймовірність того, що перевіряється число дійсно є простим.
  3. Тест Міллера-Рабіна. попередження: іноді, хоча і рідко, для декількох значень a тест помилково ідентифікує складові числа як прості.
    • Знайдіть величини s і d, такі щобN−1=2s∗d{\displaystyle n-1=2^{s}*d}.
    • Виберіть ціле число a в інтервалі 2 ≤ a ≤ n - 1.
    • Якщо ad = +1 (mod n) або -1 (mod n), то n, ймовірно, є простим числом. У цьому випадку перейдіть до результату тесту. Якщо рівність не виконується, перейдіть до наступного кроку.
    • Зведіть відповідь у квадрат (A2d{\displaystyle a^{2d}}). Якщо вийде -1 (mod n), то n, ймовірно, просте число. У цьому випадку перейдіть до результату тесту. Якщо рівність не виконується, повторіть (A4d{\displaystyle a^{4d}} і так далі) до .
    • Якщо на якомусь кроці після зведення в квадрат числа, відмінного від±1{\displaystyle \pm 1} (mod n), у вас вийшло +1 (mod n), n значить є складеним числом. Якщо A2s−1d≠±1{\displaystyle a^{2^{s-1}d}\neq \pm 1} (mod n), то n не є простим числом.
    • Результат тесту: якщо n пройшло тест, повторіть його для інших значеньa, щоб підвищити ступінь достовірності.

Частина2З 3:
Як працюють тести простоти

  1. Перебір дільників. за визначенням число n є простим лише в тому випадку, якщо воно не ділиться без залишку на 2 і інші цілі числа, крім 1 і самого себе. Наведена вище формула дозволяє видалити непотрібні кроки і заощадити час: наприклад, після перевірки того, чи ділиться число на 3, немає необхідності перевіряти, чи ділиться воно на 9.
    • Функція floor(x) округлює число x до найближчого цілого числа, яке менше або дорівнює x.
  2. Дізнайтеся про модульну арифметику. операція " x mod y "(mod є скороченням латинського слова "modulo", тобто "модуль") означає "поділити x на y і знайти залишок".[1] іншими словами, в модульній арифметиці після досягнення певної величини ,яку називаютьмодулем , числа знову "перетворюються" в нуль. Наприклад, годинник відраховує час з модулем 12: вони показують 10, 11 і 12 годин, а потім повертаються до 1.
    • У багатьох калькуляторах є клавіша mod. В кінці даного розділу показано, як вручну обчислювати цю функцію для великих чисел.
  3. Дізнайтеся про підводні камені малої теореми Ферма.всі числа, для яких не виконуються умови тесту, є складовими, проте інші числа лише ймовірно відносяться до простих. Якщо ви хочете уникнути невірних результатів, пошукайте n в списку "чисел Кармайкла" (складових чисел, які задовольняють даному тесту) і "псевдопростих чисел Ферма" (ці числа відповідають умовам тесту лише при деяких значеннях a).[2]
  4. Якщо зручно, використовуйте тест Міллера-Рабіна.хоча даний метод досить громіздкий при обчисленнях вручну, він часто використовується в комп'ютерних програмах. Він забезпечує прийнятну швидкість і дає менше помилок, ніж метод Ферма.[3] складене число не буде прийнято за просте, якщо провести розрахунки для більше ¼ значень a.[4] якщо ви випадковим способом виберете різні значення A і для всіх них тест дасть позитивний результат, можна з досить високою часткою впевненості вважати, що n є простим числом.
  5. Для великих чисел використовуйте модульну арифметику. якщо у вас під рукою немає калькулятора з функцією mod або калькулятор не розрахований на операції з такими великими числами, використовуйте властивості ступенів і модульну арифметику, щоб полегшити обчислення.[5] нижче наведено приклад для 350{\displaystyle 3^{50}} mod 50:
    • Перепишіть вираз у більш зручному вигляді:(325∗325){\displaystyle (3^{25}*3^{25})} mod 50. При розрахунках вручну можуть знадобитися подальші спрощення.
    • mod 50 = mod 50 mod 50) mod 50. Тут ми врахували властивість модульного множення.
    • mod 50 = 43.
    • mod 50 mod 50) mod 50 = mod 50.
    • mod 50.
    • .

Частина3З 3:
Використання китайської теореми про залишки

  1. Виберіть два числа.одне з чисел має бути складовим, а друге — якраз те, простоту якого ви хочете перевірити.
    • Число1 = 35
    • Число2 = 97
  2. Виберіть два значення, які більше нуля і відповідно менше чисел Число1 і Число2. ці значення не повинні збігатися один з одним.
    • Значеніе1 = 1
    • Значеніе2 = 2
  3. Обчисліть MMI (математичну мультплікативну інверсію) для Числа1 і Числа2.
    • Обчисліть MMI
      • MMI1 = Число2 ^ -1 Mod Число1
      • MMI2 = Число1 ^ -1 Mod Число2
    • Тільки для простих чисел (це дасть число для складових чисел, але воно не буде його MMI):
      • MMI1 = (Число2 ^ (Число1-2)) % Число1
      • MMI2 = (Число1 ^ (Число2-2)) % Число2
    • Наприклад:
      • MMI1 = (97 ^ 33) % 35
      • MMI2 = (35 ^ 95) % 97
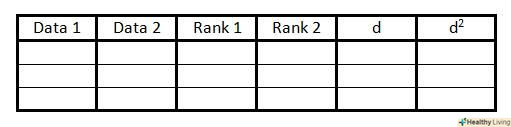
  4. Створіть таблицю для кожної MMI аж до модулів log2:
    • Для MMI1
      • F (1) = Число2 % Число1 = 97% 35 = 27
      • F(2) = F(1) * F (1) % Число1 = 27 * 27 % 35 = 29
      • F(4) = F (2) * F (2) % Число1 = 29 * 29 % 35 = 1
      • F (8) = F (4) * F(4) % Число1 = 1 * 1 % 35 = 1
      • F(16) =F (8) * F (8) % Число1 = 1 * 1 % 35 = 1
      • F(32) =F(16) * F (16) % Число1 = 1 * 1 % 35 = 1
    • Обчисліть парні Число1 - 2
      • 35 -2 = 33 (10001) за основою 2
      • MMI1 = F(33) = F(32) * F(1) mod 35
      • MMI1 = F(33) = 1 * 27 mod 35
      • MMI1 = 27
    • Для MMI2
      • F (1) = Число1 % Число2 = 35 % 97 = 35
      • F (2) = F (1) * F(1) % Число2 = 35 * 35 mod 97 = 61
      • F(4) = F (2) * F (2) % Число2 = 61 * 61 mod 97 = 35
      • F (8) = F (4) * F(4) % Число2 = 35 * 35 mod 97 = 61
      • F(16) = F (8) * F(8) % Число2 = 61 * 61 mod 97 = 35
      • F(32) = F (16) * F(16) % Число2 = 35 * 35 mod 97 = 61
      • F (64) = F (32) * F(32) % Число2 = 61 * 61 mod 97 = 35
      • F(128) = F (64) * F (64) % Число2 = 35 * 35 mod 97 = 61
    • Обчисліть парні Число2 - 2
      • 97 – 2 = 95 = (1011111) на підставі 2
      • MMI2 = (((((F(64) * F(16) % 97) * F(8) % 97) * F(4) % 97) * F(2) % 97) * F(1) % 97)
      • MMI2 = (((((35 * 35) %97) * 61) % 97) * 35 % 97) * 61 % 97) * 35 % 97)
      • MMI2 = 61
  5. Обчисліть (Значеніе1 * Число2 * MMI1 + Значеніе2 * Число1 * MMI2) % (Число1 * Число2)
    • Відповідь = (1 * 97 * 27 + 2 * 35 * 61) % (97 * 35)
    • Відповідь = (2619 + 4270) % 3395
    • Відповідь = 99
  6. Перевірте, що Число1 не є простим
    • Обчисліть (відповідь – Значення1) % Число1
    • 99 – 1 % 35 = 28
    • Так як 28 більше 0, то 35 не є простим числом.
  7. Перевірте, що Число2 є простим.
    • Обчисліть (відповідь – Значення2) % Число2
    • 99 – 2 % 97 = 0
    • Так як 0 дорівнює 0, то 97-швидше за все просте число.
  8. Повторіть кроки з 1 по 7 щонайменше ще два рази.
    • Якщо в кроці 7 виходить 0:
      • Використовуйте інше Число1, якщо Число1 не є простим.
      • Використовуйте інше Число1, якщо Число1 є простим. В цьому випадку в кроках 6 і 7 повинен вийти 0.
      • Використовуйте інші Значення1 і Значення2.
    • Якщо в кроці 7 ви постійно отримуєте 0, то з дуже великою ймовірністю Число2 є простим.
    • Кроки з 1 по 7 можуть призвести до помилки, якщо Число1 не є простим, а Число2 є дільником Числа1. Описаний метод працює у всіх випадках, коли обидва числа є простими.
    • Причина, по якій необхідно повторювати кроки з 1 по 7, полягає в тому, що в деяких випадках, навіть якщо Число1 і Число 2 не є простими, в кроці 7 Ви отримаєте 0 (для одного або обох чисел). Це трапляється рідко. Виберіть інше Число1( складене), і якщо Число2 не є простим, тоді Число2 не дорівнюватиме нулю в кроці 7 (за винятком випадку, коли Число1 є дільником Числа2 — тут прості числа завжди дорівнюватимуть нулю в кроці 7).

Поради

  • Прості числа від 168 до 1000: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.[6]
  • Хоча при роботі з великими числами перебір дільників є трудомістким способом перевірки, він досить ефективний у випадку малих чисел. Навіть у випадку великих чисел починають з тестування малих дільників, а потім переходять до більш складних методів перевірки простоти чисел (якщо Малі дільники не знайдені).

Що вам знадобиться

  • папір, ручка або комп'ютер

Джерела

  1. ↑ Http://betterexplained.com/articles/fun-with-modular-arithmetic/
  2. ↑ Http://mathworld.wolfram.com/FermatsLittleTheorem.html
  3. ↑ Http://www.cs.cornell.edu/courses/cs4820/2010sp/handouts/MillerRabin.pdf
  4. ↑ Https://books.google.com/books?id=QbVtCQAAQBAJ&#amp;dq=miller-rabin+1/4+false+positives
  5. ↑ Https://www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/modular-exponentiation
  6. ↑ Online Encyclopedia of Integer Sequences, A000040
  7. Topcoder.com - джерело з кодами і описом викладених вище методів
  8. Online Prime Number Checker - перевірка чисел, що містять до 5000 цифр

Ще почитати: