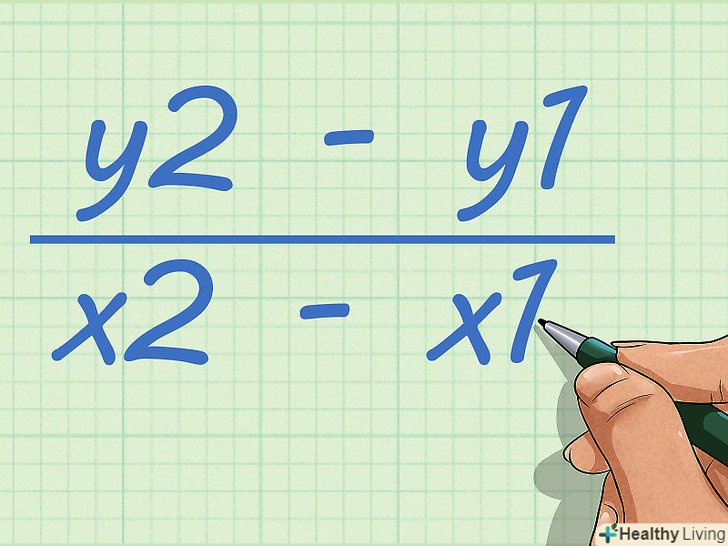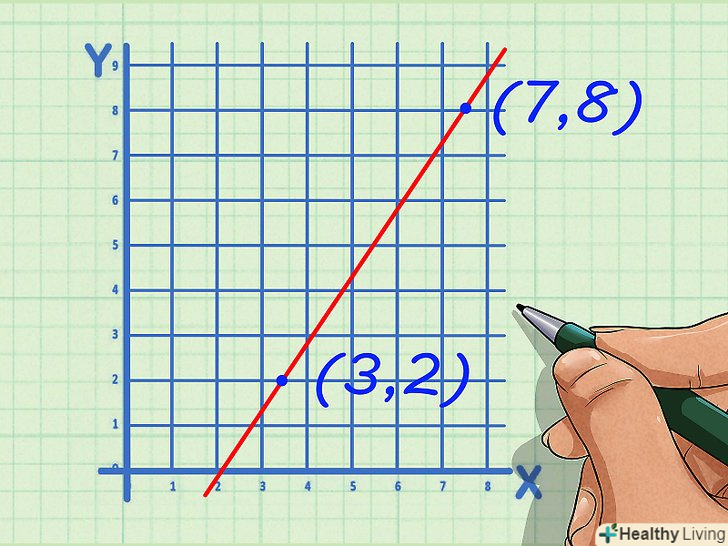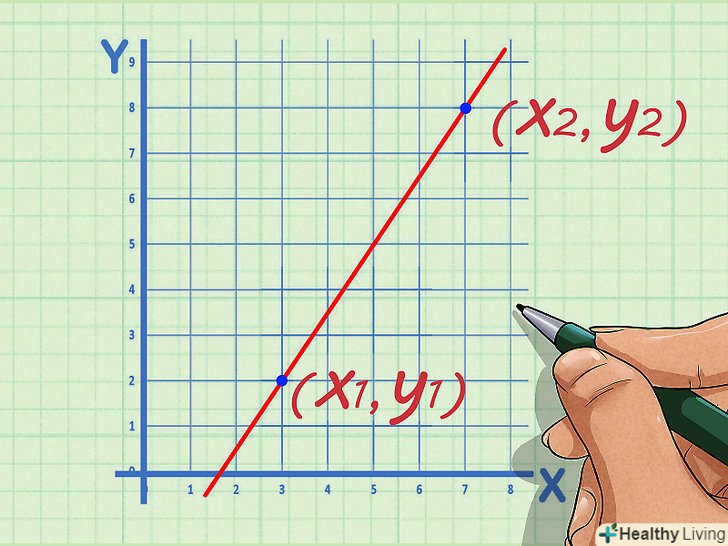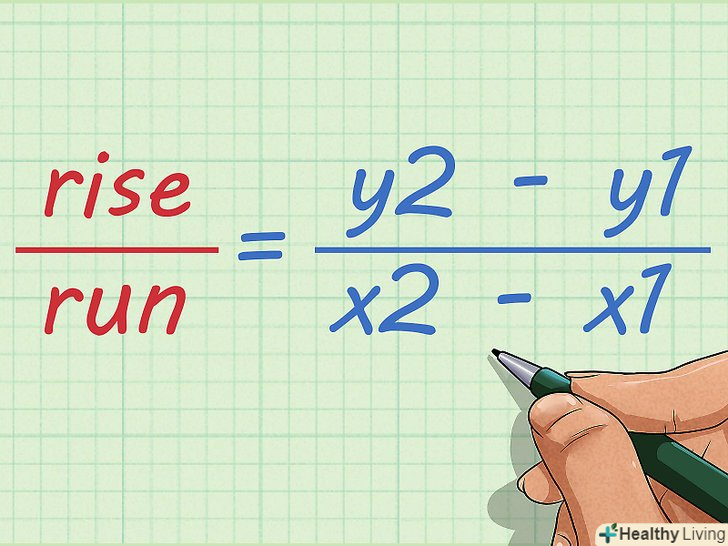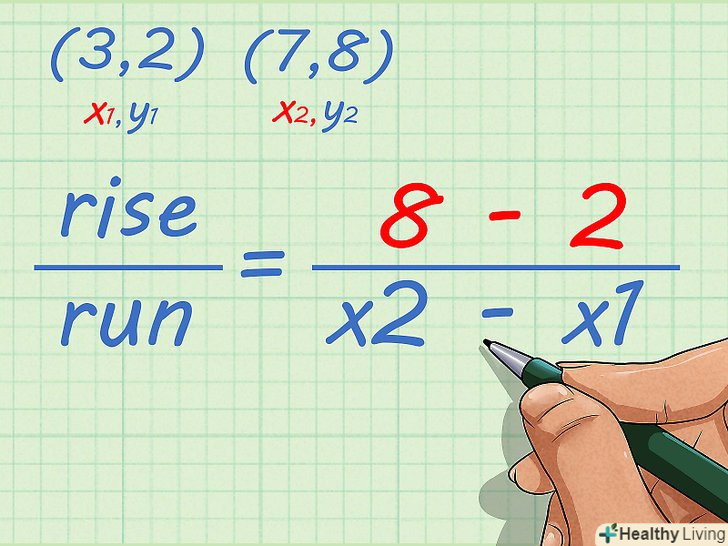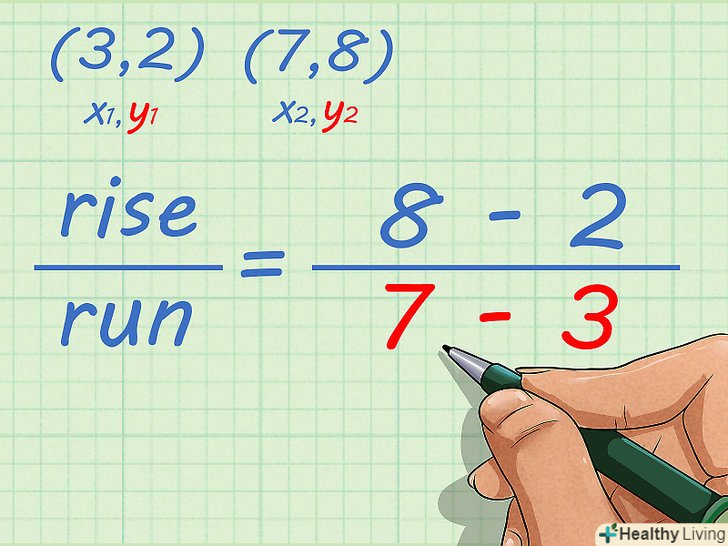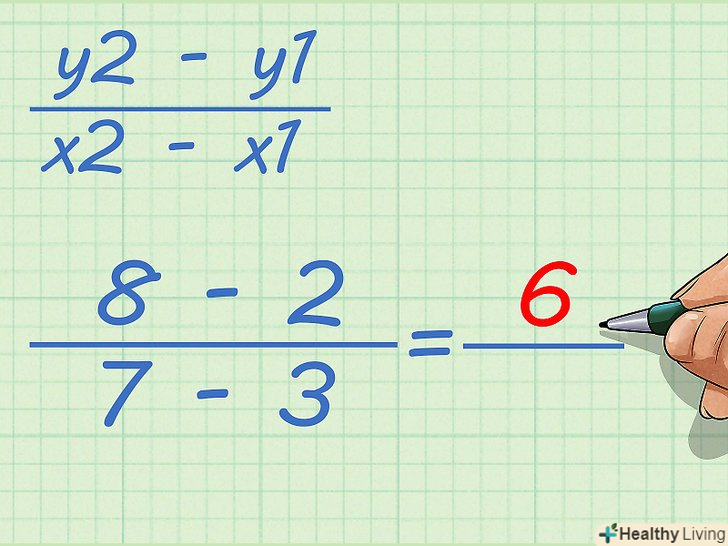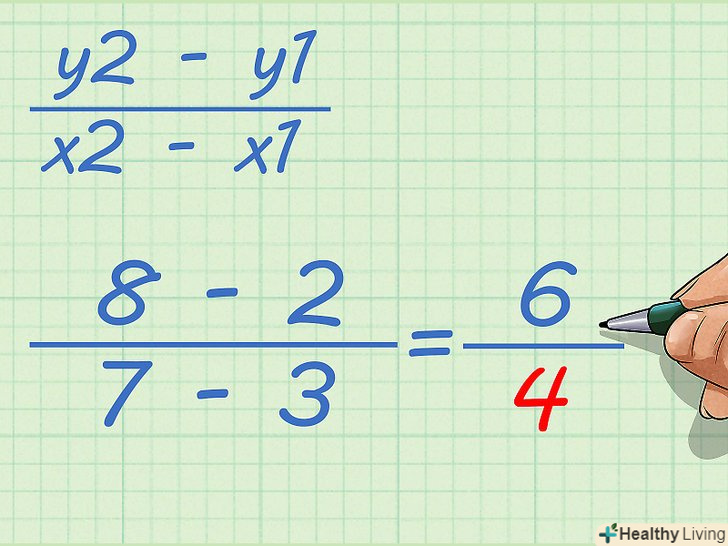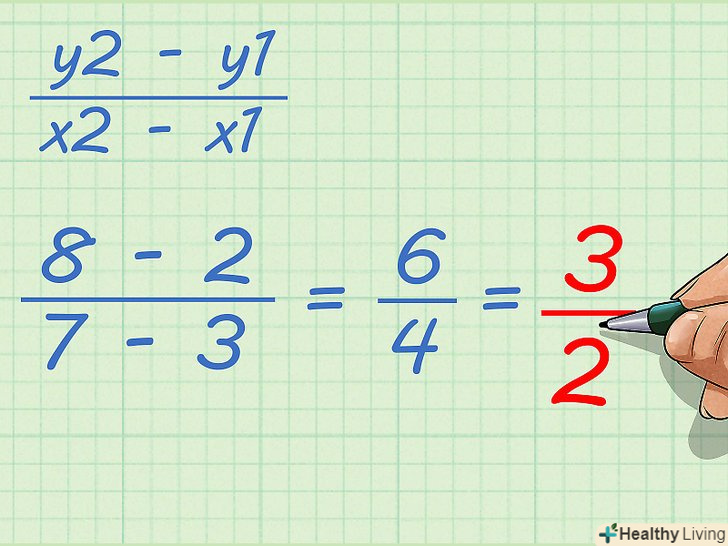Знаходження кута нахилу прямої – це один з найважливіших навичок в геометрії, необхідний для побудови графіка лінійної функції або для визначення координат точок перетину прямої з осями X і Y. Кут нахилу прямої визначає швидкість її зростання або убування,[1] тобто як швидко пряма переміщається по вертикалі в залежності від руху по горизонталі. Кут нахилу прямої легко обчислюється за координатами двох точок, що лежать на цій прямій.
Кроки
Частина1 З 2:
Запис завдання
Частина1 З 2:
 Зрозумійте формулу для обчислення кутового коефіцієнта.кутовий коефіцієнт дорівнює тангенсу кута нахилу прямої, який вона утворює з віссю Х, і обчислюється як відношення вертикальної відстані між двома точками до горизонтальної відстані між двома точками.
Зрозумійте формулу для обчислення кутового коефіцієнта.кутовий коефіцієнт дорівнює тангенсу кута нахилу прямої, який вона утворює з віссю Х, і обчислюється як відношення вертикальної відстані між двома точками до горизонтальної відстані між двома точками. Виберіть дві точки і знайдіть їх координати. можна вибрати будь-які дві точки, що лежать на прямій.
Виберіть дві точки і знайдіть їх координати. можна вибрати будь-які дві точки, що лежать на прямій.- Скористайтеся цим методом, якщо дані тільки координати двох точок (без графіка).
- Координати записуються у вигляді
, де
– координата по осі Х (горизонтальна вісь),
– координата по осі Y (вертикальна вісь).
- Наприклад, дано дві точки з наступними координатами:
і
.
 Задайте порядок точок (відносно один одного).одна точка буде першою точкою, а інша-другою. Не має значення, яка точка буде першою, а яка другий – головне не переплутати їх порядок в процесі обчислення.[2]
Задайте порядок точок (відносно один одного).одна точка буде першою точкою, а інша-другою. Не має значення, яка точка буде першою, а яка другий – головне не переплутати їх порядок в процесі обчислення.[2]- Координати першої точки позначимо як
, а координати другої точки – як
.
- Координати першої точки позначимо як
 Запишіть формулу для обчислення кутового коефіцієнта. Формула:
Запишіть формулу для обчислення кутового коефіцієнта. Формула:, де VR – вертикальна відстань, обумовлене зміною координати «у», GR – горизонтальна відстань, що визначається зміною координати "х".[3]
Частина2 З 2:
Обчислення кута нахилу прямої
Частина2 З 2:

- Наприклад, якщо координати першої точки:
, а координати другої точки:
, то формула прийме наступний вигляд:
- Наприклад, якщо координати першої точки:

- Наприклад, якщо координати першої точки:
, а координати другої точки:
, то формула прийме наступний вигляд:
- Наприклад, якщо координати першої точки:
 Відніміть координати "у".ви знайдете вертикальну відстань.
Відніміть координати "у".ви знайдете вертикальну відстань.- Наприклад, якщо координати "у":
і
, то вертикальне відстань:
.
- Наприклад, якщо координати "у":
 Відніміть координати "х".ви знайдете горизонтальну відстань.
Відніміть координати "х".ви знайдете горизонтальну відстань.- Наприклад, якщо координати "х":
і
, то горизонтальне відстань:
.
- Наприклад, якщо координати "х":
 Якщо можливо, скоротіть дріб. Ви знайдете кутовий коефіцієнт.
Якщо можливо, скоротіть дріб. Ви знайдете кутовий коефіцієнт.- Якщо ви не знаєте, як скоротити дроби, прочитайте цю статтю.
- У нашому прикладі дріб
скорочується до
, тобто кутовий коефіцієнт прямої, що проходить через точки з координатами
і
, дорівнює
або
. Щоб обчислити кут нахилу прямої, зі знайденого значення візьміть арктангенс. У нашому прикладі: arctg(1,5) = 56,3 градусів.
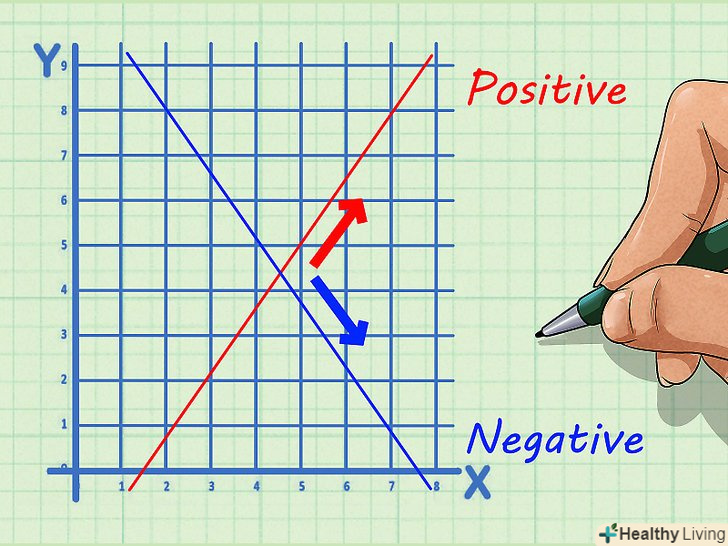
 Звертайте увагу на негативні числа.кутовий коефіцієнт може бути позитивним або негативним. У разі позитивного значення пряма зростає (рухається вгору зліва направо); в разі негативного значення пряма убуває (рухається вниз зліва направо).
Звертайте увагу на негативні числа.кутовий коефіцієнт може бути позитивним або негативним. У разі позитивного значення пряма зростає (рухається вгору зліва направо); в разі негативного значення пряма убуває (рухається вниз зліва направо).- Пам'ятайте, що якщо і в чисельнику, і в знаменнику стоять негативні числа, то результат буде позитивним.
- Якщо в чисельнику або в знаменнику стоїть негативне число, то результат буде негативним.
 Перевірте відповідь.для цього виміряйте або порахуйте (за шкалами осей) вертикальне і горизонтальне відстані. Якщо вони збіглися з обчисленими, то відповідь правильна.
Перевірте відповідь.для цього виміряйте або порахуйте (за шкалами осей) вертикальне і горизонтальне відстані. Якщо вони збіглися з обчисленими, то відповідь правильна.- Якщо виміряні або пораховані вертикальне і горизонтальне відстані не збіглися з обчисленими, то відповідь не правильна.
Поради
- Кутовий коефіцієнт позначається як
. Обчисливши кутовий коефіцієнт, можна записати функцію прямої:
, де
– кутовий коефіцієнт,
– координата " у " точки перетину прямої з віссю Y.
Схожі статті
- Як використовувати формулу відстані для розрахунку довжини лінії
- Як визначити приналежність трьох даних сторін одному трикутнику
- Як знайти відстань між двома точками
- Як знайти кут між векторами
- Як знайти величину вектора
- Як знайти гіпотенузу
- Як знайти серединний перпендикуляр
- Як знайти рівняння прямої
- Як знайти вершину параболи квадратного рівняння